一个B 型丛代数的几何实现

张杰，戚茜

（北京理工大学 数学与统计学院，北京 102400）

丛代数是由FOMIN 等[1]提出的一类由丛变量生成的交换代数.最初，研究丛代数是为了寻找一个研究李代数的全正性和典范基[2-3]的工具.丛代数在许多数学领域均有应用，例如，李理论、箭图表示、泊松几何、组合学等其他理论[4-7].

FOMIN 等[1]证明，丛代数的任何丛变量都可以用洛朗多项式由初始丛变量x1,x2,···,xn表示，即

式中：f(x1,x2,···,xn)∈Z[x1,x2,···,xn]，并且di∈Z≥0.找到丛变量的丛扩展公式已经成为许多数学家关心的课题，例如，FOMIN 等提出的正性猜想[1]被LEE 等[8]通过给出相应的丛变量的丛扩展公式所证明；MUSIKER[9]利用图GT,γ的完美匹配给出了丛变量的丛扩展公式；一个丛变量的图理论组合解释[10]被MUSIKER 利用从而给出了有限维丛代数的丛扩展公式，其中包括B型丛代数.

注意到DUPONT[11]分析了简单带状丛代数和非简单带状丛代数之间的关系，从而可以推测出一些B型丛代数的性质.为了给出丛代数 B的丛变量的丛扩展公式，首先研究由一个 (2n+2)- 多边形P产生的丛代数 A ，并考虑 A 的 丛变量和丛到 B的丛变量和丛的投影.

本文，考虑一个 (2n+2)- 多边形P和它的三角剖分Γ={τ1,τ2,···,τ2n-1}，如图1.

图1 P的 三角剖分ΓFig.1 Triangulation Γ ofP

主要结果如下：

首先，定义一个映射ð(见第 2节)，它给出了 Γ的对角线和 B的初始丛变量之间的对应关系，然后通过给出P中任意一条对角线 γ的多项式Eγ的定义(定义5)，为非初始丛变量提供一个准确的公式.

定理1(2n+2)- 多边形P的每条对角线 γ均诱导一个B型 丛代数 B的 丛变量Eγ.

接下来，通过考虑一个P的对角线的置换 σ (详见第 2节 )，给出 σ-不变三角剖分的定义(定义6).易知，对于P的任何对角线 β，β 和 σ(β)在同一个轨道上.接下来，阐明由同一轨道的对角线所产生的丛变量之间的关系.

推论1σ-不变的三角剖分 Γ的同一个轨道的对角线诱导相同 B的丛变量.

通过给出轨道翻转(Γ)的 定义(定义7)，呈现B的丛在k∈[1，n]方向上突变的几何实现.

推论2(Γ)是 一个 σ-不变的三角剖分.

接下来，用交换图来构建 σ-不变的三角剖分 Γ的轨道翻转和 B的丛的突变对应.

定 理2Γ 在 τk方 向 上 的 轨 道 翻 转(Γ)对 应 B的丛在k方 向 上 的 突 变 µk().同 时，存 在 一 个 映 射ð′:Γ′→，满足 µkð(Γ)=ð′(Γ)，使下方交换图成立，如图2.

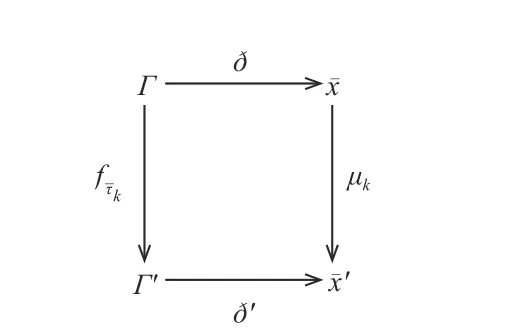
图2 交换图Fig.2 Commutative diagram

最后，介绍B型丛代数的丛和 σ-不变的三角剖分之间的关系.

推论4P的 σ -不变的三角剖分集合与 B 的丛的集合之间存在一个双射.

本文的结果适用于任何 σ-不变的三角剖分，不仅仅局限于三角剖分 Γ.为方便讨论，本文将三角剖分固定为 Γ.

1 B 型丛代数

首先，介绍由赋值箭图定义的丛代数的相关概念.为了给出定义，先给定一些记号，令F :=Q(x1,x2,···,xn)为 有n个 变量的有理函数域，记 [1,n]为正整数集合 {1,2,···,n-1,n}.

为了给出丛代数的定义，首先介绍种子的概念.

定义2(种子)一个种子即为包含以下数据的一个二元对 (x,Q)：

①Q是一个含有n个顶点的赋值箭图；

②x=(x1,x2,···,xn)是 有理函数域 F的自由生成集，x与xi分别被称作丛和丛变量.

一个新的种子可以由以下操作得到.vjk)∈N×N.

III)如果vikvk j=vij，则消去箭头 (j,i)和它的赋值.

注意一个赋值箭图经过突变之后仍是一个赋值箭图，并且 µ2k(Q)=Q.现在介绍由赋值箭图定义的丛代数.首先，对于赋值箭图Q来说，取一个初始种子(x=(x1，x2,···,xn),Q).

定义4(赋值箭图定义的丛代数) 由初始种子(x,Q)定 义的丛代数 A(Q)=A(x,Q)是由初始丛变量经过所有可能的突变得到的丛变量生成的 Z-子代数.

本文，主要研究B型丛代数 B=A(Q)，其中Q是一个赋值箭图，它的底图如图3 所示.

图3 赋值箭图Q的底图Fig.3 Underlying graph of valued quiverQ

2 一个B 型丛代数的几何实现

图4 P的三角剖分子图Γ[i,j]Fig.4 Triangulated subgraph Γ[i,j] ofP

图5 箭图QΓFig.5 Quiver QΓ

图6 赋值箭图Fig.6 Valued quiver

因此，可以定义一个与三角剖分 Γ 有关的B型丛代 数 B=B((x1,x2,···,xn)，.同 时，定 义 一 个 映 射ð:Γ →

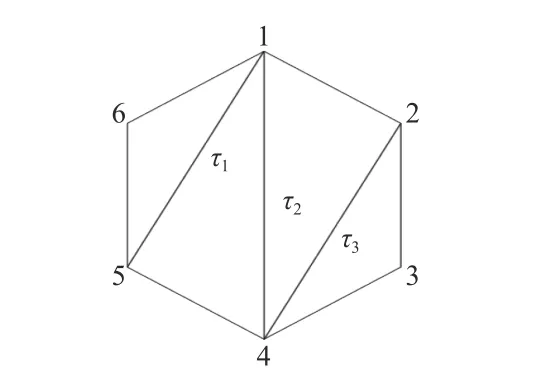
图7 六边形的一个三角剖分6Fig.7 Triangulation of the -polygon

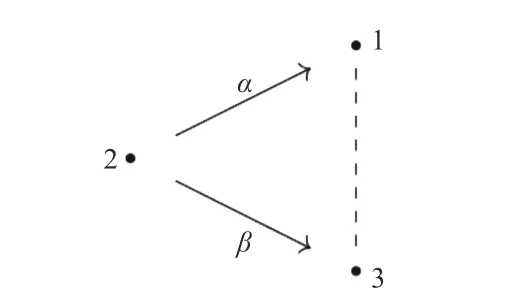
图8 箭图Fig.8 Quiver

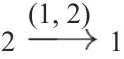
图9 赋值箭图Fig.9 Valued quiver

因此，定义一个与 Γ 有关的B型 丛代数B=B((x1,x2),).接下来，定义映射ð：Γ →，满足

任 取 一 个 穿 过 对 角 线 τ2和 τ3的 对 角 线 γ(图10)，相应的三角剖分子图 Γ[2-3]如图11 所示.

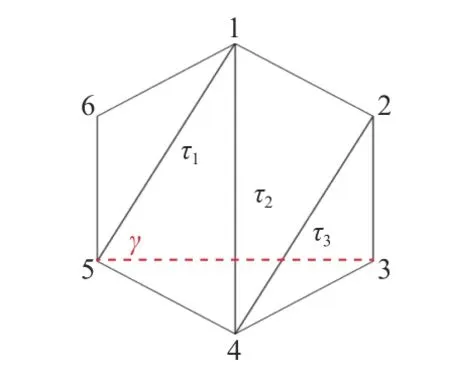
图10 三角剖分Fig.10 Triangulation

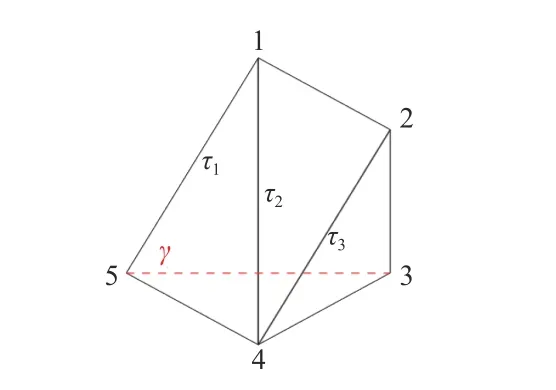
图11 三角剖分子图 Γ[2-3]Fig.11 Triangulated subgraph Γ[2-3]

由定理3 可以得到 B的 丛变量xγ的丛扩展公式

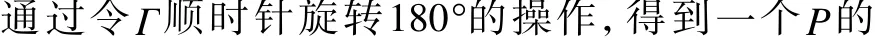
图12 交换图Fig.12 Commutative diagram

即交换图13 成立，将这两个交换图组合在一起，则有交换图14，其中，ð=πℓ.

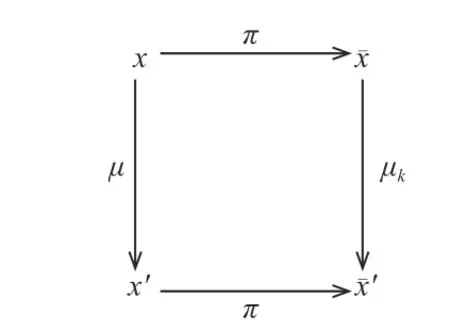
图13 交换图Fig.13 Commutative diagram

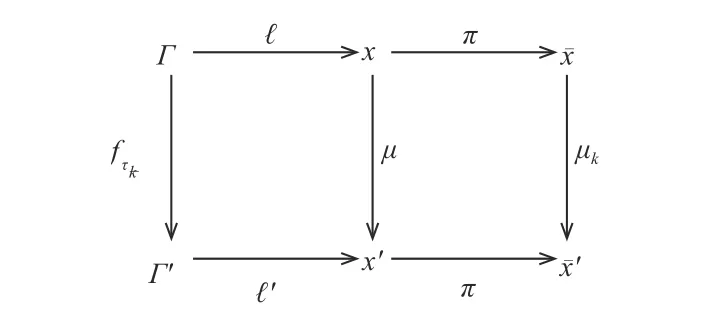
图14 交换图Fig.14 Commutative diagram

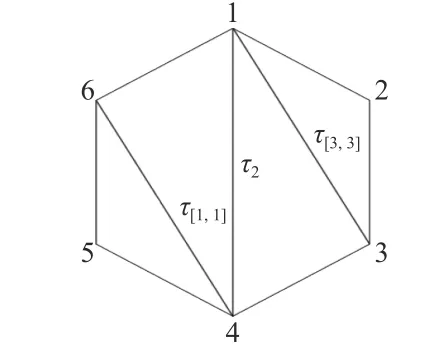
图15 三角剖分(Γ)Fig.15 TriangulationΓ)

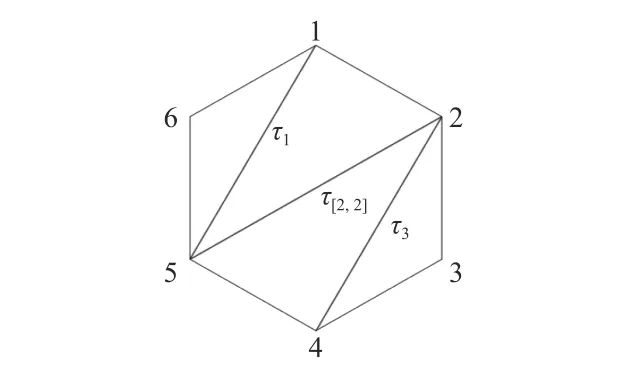
图16 三角剖分2(Γ)Fig.16 TriangulationΓ)