一类免碰撞编队集群模型
2023-05-10肖宏琪肖其珍刘宏亮
肖宏琪,肖其珍,刘宏亮
(南华大学 数理学院,湖南 衡阳 421001)
0 引 言

(1)

f:(d0,∞)→[0,∞)满足局部利普希茨连续条件,且

(2)f(r)=0,r≥d1,
其中d0,d1为常数。而φ具有如下形式
是否存在满足某种条件的k将决定系统(1)能否形成目标编队。本文受到参考文献[10]的启发,考虑一类非线性多智能体系统的免碰撞编队问题。
1 模型介绍和预备知识
1.1 模型介绍

(2)
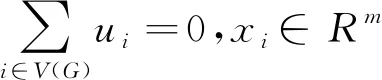
定义1 对于初值(x0,v0),系统(2)形成了免碰撞集群指的是
存在C1,C2>0,使得
1.2 图论知识
一般多智能体系统的拓扑结构可以由代数图来刻画,用点表示智能体,而连线表示智能体之间的通信。本文中考虑的所有图均是有限的简单图,其他未说明的概念和术语参见参考文献[11]。
图是指一个有序三元组(V(G),E(G),ψ(G))。集合V(G)表示图G的点集,其中元素称为图G的点或顶点;集合E(G)表示图G的边集,其中元素称为图G的边;ψ(G)是关联函数,它使G的每条边对应于G的无序顶点对。若两个顶点是一条边的两个端点,则称这两个点是相邻的。若一个点是一条边的某个端点,则称这个点与这条边相关联。若以两个点为端点的边的数目大于两条,则称这些边为重边。不含重边的图称为简单图。
图G中的一条途径是指有限的相关联的点边序列v0e1v1e2v2e3v3…vk-1ekvk。若途径中出现的边均不相同,顶点也不相同,则称这条迹为路。若图G中任意两个点之间总有一条路连接这两个点,则称图G是连通的。顶点vi的相邻顶点集合记为Ni,本文用j∈Ni表示vj是vi的邻居。对于相关联的点边序列vieivj在本文中直接用(i,j)表示边ei。在本文中,无向图G中当(i,j)∈E(G)时,(j,i)∈E(G)。
1.3 几个引理

对系统
(3)
有如下结论
引理2[13]在系统(3)中,f(t,x)关于t分段连续,关于x满足局部利普希茨条件即对任意x,y∈B={x∈Rn|‖x-x0‖≤r},任意t∈[t0,t1],存在常数L有
‖f(t,x)-f(t,y)‖≤L‖x-y‖,
那么存在ω>0,使得系统(3)在[t0,t0+ω]存在唯一解。
引理3[13]假设W为D⊂Rn的一个紧子集,对任意的x∈D和t>t0,f(t,x)关于t都是分段连续的,关于x都满足局部利普希茨条件。若当x0∈W时,系统(3)的解都位于W内,则系统(3)在t>t0上存在唯一解。
2 主要结论
本小节,给出主要结论。
(a)先考虑
(4)
此时,有
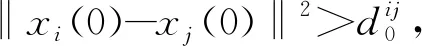

记
于是,系统(2)取控制器(4)可改写成
(5)
此时取能量函数
(6)
为了证明定理1先给出以下引理,即对于系统(2)取控制器(4)来说,E(x(t),v(t))是一个关于t的单调减函数。
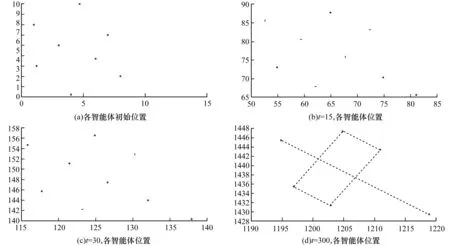
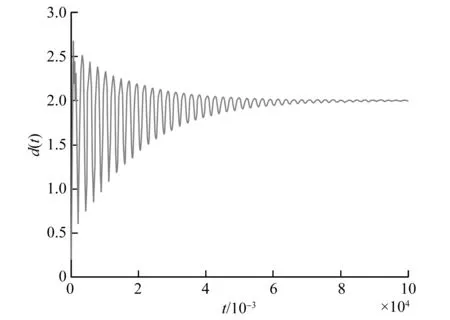
引理4 假设(x(t),v(t))在t∈[0,T)上是系统(2)取控制器(4)的一个解,其中0 即E(x(t),v(t))是一个关于t的单调递减函数。 证明:对于0≤t 联立式(6),有 ‖vi-vj‖2。 证毕。 下面给出定理1的证明。 否则与fij性质(f1),(f2),(f3),(f4)矛盾。 所以当0≤t≤T时,fij(‖xi-xj‖2)有界。且存在一个正数φ0使得 0<φ0≤φ(‖xi-xj‖)<∞。 (7) 同时有: 这表明 即‖vi‖有界,那么‖vi-vj‖有界,故存在M>0使得 (8) 表明T=+∞。对于系统(2)取控制器(4)的解(x(t),v(t))(0 注意到系统(2)取控制器(4)的右端部分在开集D中连续(D∶={(x,v)∈RmN×RmN:d0<‖Xi-Xj‖,i≠j}),显然Ω⊆D。根据引理3知道系统(2)取控制器(4)的解在T=+∞时存在且唯一。 接下来证明各智能体速度趋于一致。由引理4有 ‖vi-vj‖2ds≤E(0)。 联立式(7),同时E(x(0),v(0))≥0,又由于G是连通图,则对于i,j∈V(G)有 从而 (b)当m=1时,控制输入ui分别取 (9) 其中fij定义与(a)中fij定义一致。 此时,有 证明:对于系统(2)取控制器(9),假设,x1(0)>…>xN(0)(或者x1(0)<… u1=f12((x1-x2)2)(x1-x2), ui=fi(i-1)((xi-xi-1)2)(xi-xi-1)+ fi(i+1)((xi-xi+1)2)(xi-xi+1)(1 uN=fN(N-1)((xN-xN-1)2)(xN-xN-1), 在本节使用matlab给出仿真实例验证理论结果。 (10) 对于系统(10),取9个二维中的粒子,各个维度对应的连接矩阵均为如下 图1有4张分图,图1(a)表示各智能体初始位置;图1(b)表示t=15时,各智能体位置;图1(c)表示t=30,各智能体位置;图1(d)表示t=300,各智能体位置,并且此时智能体形成了一个“中”字形。 图1 智能体的位移 从图2中可以看到所有的时间t都有d(t)>0;即智能体之间不会发生碰撞。 图2 粒子的最小位移差 图3有2张图,图3(a)表示各智能体x维度上速度变化;图3(b)表示各智能体y维度上速度变化,可以看出来各智能体速度趋于一致。 图3 智能体的速度 在满足一定条件下,一类粒子间键合力(a)将使得多智能体系统达到免碰撞集群,在此基础上,得到了在满足一定条件下,一类粒子间作用力(b)将使得智能体在1维空间内避免碰撞,同时形成特定编队。也就是说如果智能体系统在各个维度均有此类作用力,那么将在多维形成特定编队。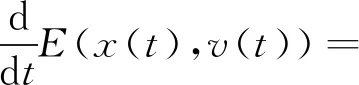
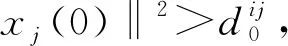




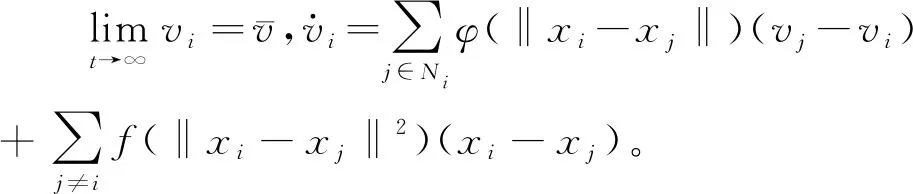


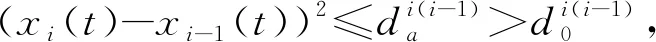
3 举例和仿真




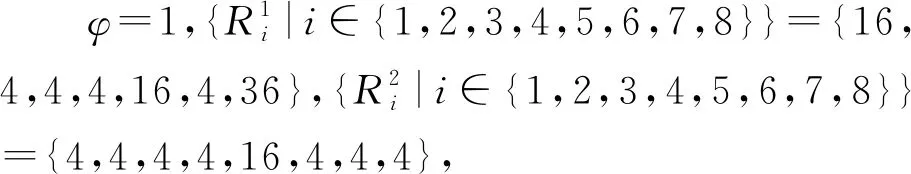

4 结 论
