基于随机骨料模型的混凝土塑性损伤耦合力学性能研究
2023-05-10杨帅东高月明陈文昭
杨帅东,高月明,2,曾 涛,陈文昭
(1.珠江水利委员会珠江水利科学研究院 水利工程研究所,广东 广州 510611;2.广东华南水电高新技术开发有限公司,广东 广州 510611;3.西安建筑科技大学 土木工程系,陕西 西安 710055;4.南华大学 土木工程学院,湖南 衡阳 421001)
0 引 言
混凝土是由粗骨料、砂浆基体、薄弱界面层、孔隙及裂纹等组成的非均质多相复合材料,其宏观力学性能一直是国内外学者们研究探索的一个重要课题[1]。鉴于混凝土高度不均匀性的细观结构以及组分复杂的力学性能,为了获取相应的材料和力学参数,实际工程中往往需要进行大量的实验,如单轴拉压、巴西劈裂等。同时,实际过程中往往受实验条件的限制,存在一定的局限性。因此,采用数值模拟的方法有助于科研和工程人员全方面地了解混凝土服役期的力学性能,更好地为工程实践服务。
目前流行的数值模拟方法主要包括以下几类:
1)格构模型(lattice model)
20世纪末,Schlangen和Van Mier率先利用格构模型来进行混凝土断裂破坏研究。该模型主要将砂浆基体理想为格构。在受荷过程中格构可以断裂,从而模拟材料在受荷过程中的破坏。但是该模型在模拟受压破坏效果较差[2]。
2)随机粒子模型(random particle model)
随机粒子模型由著名学者P.A.Cundall等[3]提出,后经各国学者发展成为当今流行的离散元。该方法在多数情况下可以很好地模拟材料单拉和单压条件下的力学性能。但该方法假定颗粒材料是不会发生破坏的弹性体,因而当骨料力学较差时,和实验数据相差较大。
3)M-H细观力学模型(micromechanical model,M-H)
M-H细观力学模型由A.R.Mohamed和W.Hansen建立[4],用来研究混凝土细观结构及破坏机制。该方法假定材料的破坏为单元的受拉破坏且裂缝的生成、演化和破裂都是由受拉荷载控制,因而该方法同样不适用于模拟受压荷载控制的破坏。
4)刚体弹簧元模型(rigid body spring element model)
刚体弹簧元是T.Kawai基于离散单元法建立[5]。模型由离散的刚体多边形单元和单元边界处的弹簧单元连接而成。该方法主要问题在于处理非线性问题时收敛性较困难。
5)梁-颗粒模型(beam aggregate model)
梁-颗粒模型同样基于离散单元法提出[6]。该方法的主要特色在于单元形状较为自由,可为圆形、三角形或者voronoi多边形。各单元之间通过梁-颗粒模拟。在加载过程中,材料破坏主要发生连接单元的梁之间。
6)微平面模型(microplane model)
微平面模型由Z.P.Bazant教授提出[2]。该方法已经提出了十几个版本,可以模拟混凝土材料在不同工况下的破坏模式。该方法的主要缺点为待标定的参数较多,精度尚待验证。
7)随机骨料模型(random aggregate model)
随机骨料模型由砂浆基质和随机生成骨料共同组成。目前该方法已经可以针对不同的骨料集配和骨料形状进行分析。将该模型导入到常规的商业有限元程序软件后,可借助于有限元强大的非线性分析能力,模拟塑性、粘塑性和损伤等多种工况。
本文为了减少其他因素对结果的影响,假定骨料为球形,暂忽略骨料和砂浆之间的界面效应。
1 几何模型
瓦拉文(J.C.Walraven)[7]建立了混凝土试件空间内骨料级配及质量分数与其截面所切割的骨料面积的关系,使得计算模型从三维简化为二维。二维混凝土骨料模型构建主要基于随机顺序添加算法(random sequential addition,RSA)[8]。该方法的基本思路如下:
1)确定每一个级配骨料的数量
①基于瓦拉文公式(1),试件内任意点骨料粒径D小于某一特征粒径D0的概率为:
(1)
其中,PK为骨料的质量分数,Dmax为骨料最大粒径,mm。
②基于级配的粒径区间,确定该粒径区间骨料所占面积。
③假定骨料为球形且大小一致,确定相应级配区间骨料数量。
2)骨料模型的生成
不间断地往某一个区域ABCD添加一些随机生成的颗粒pi,如图1所示,为了保证球形颗粒不与边界相交且新生成的球与之前存在的球不重叠,需要满足以下两个条件:
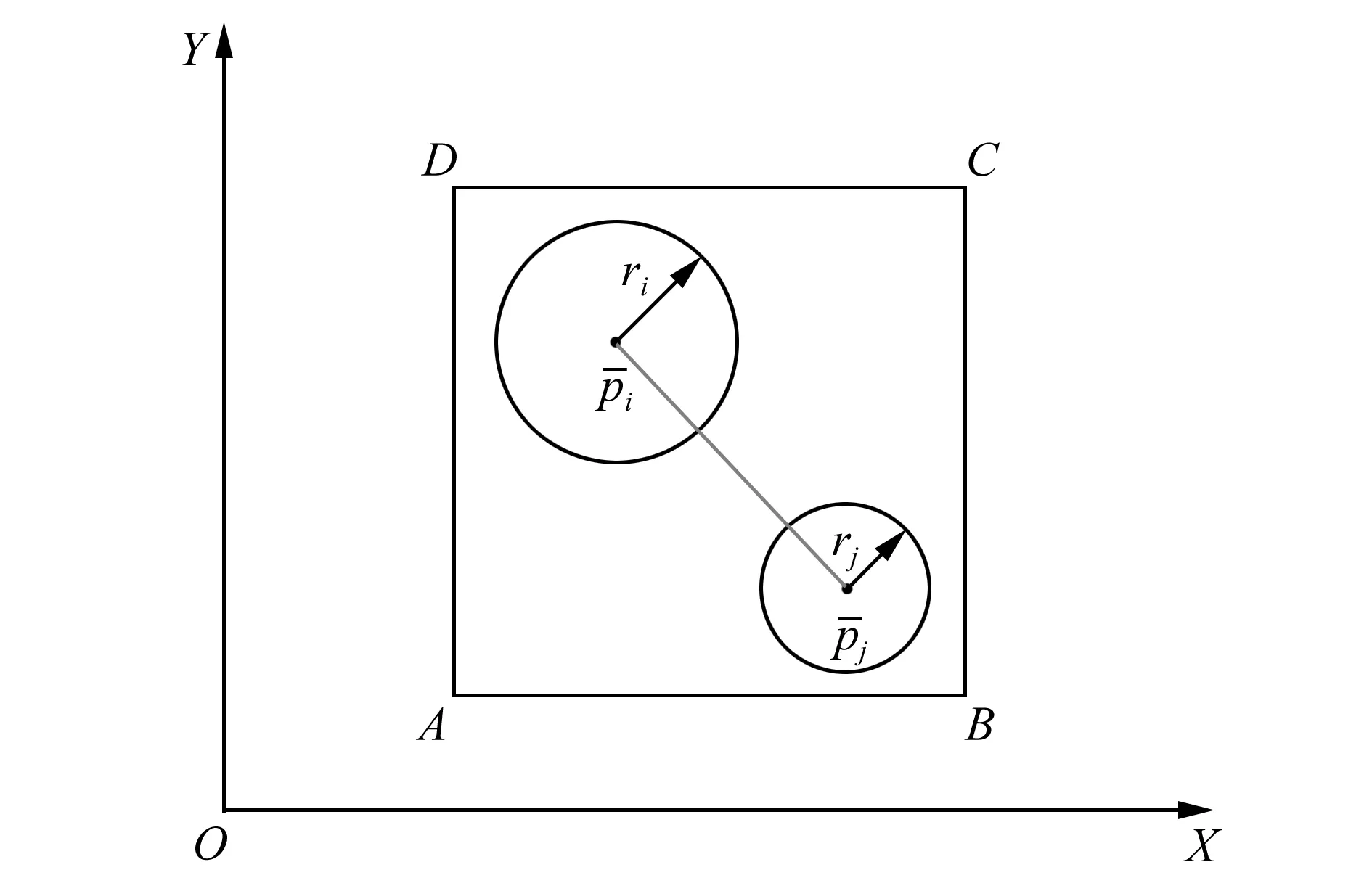
图1 骨料与区域、骨料与骨料之间的相对关系
(2)
(3)
其中,条件(2)保证所生成的球形骨料和区域不相交,条件(3)保证球形颗粒之间不重叠。
3)像素化网格生成
当骨料质量分数较高时,骨料之间较小的间隙会引起网格的畸形,从而导致计算量增加甚至计算的不收敛。为了克服这一问题,本文采用像素化网格,即将大小为150 mm×150 mm混凝土划分为150×150的正方形单元,再将生成的骨料模型投影到像素网格区域(如图2所示)。网格的属性通过正方形单元节点的位置来判定。本文假定若正方形单元形心位于球形骨料内部,则该单元属性为骨料,反之则为砂浆。像素网格可一定程度上加快计算速度,但在边界部分会损失一定的精度。骨料模型的构建可通过Abaqus自带的Python语言进行二次开发。值得注意的是,进行骨料投放时应遵循先大后小的原则。
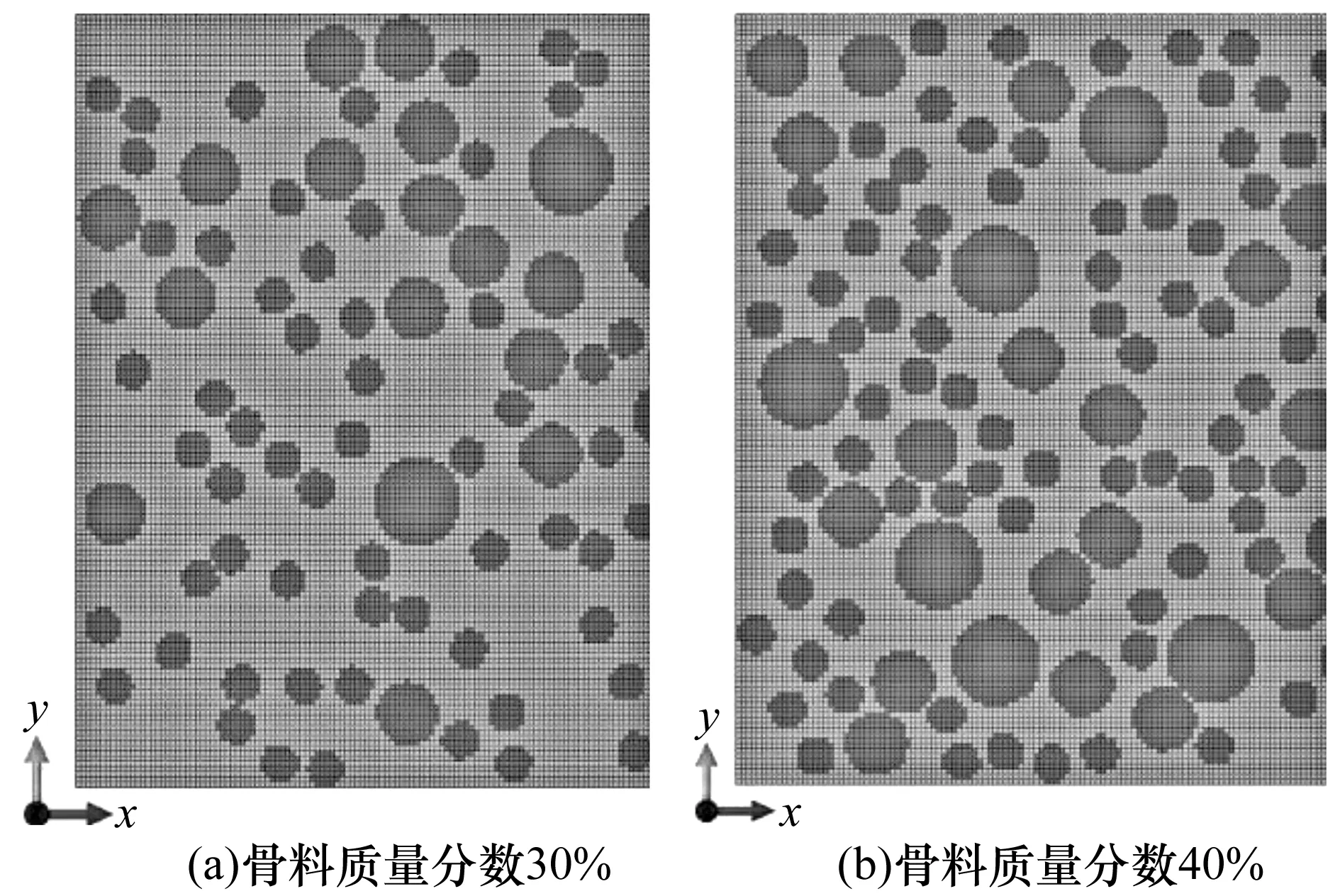
图2 像素网格
2 本构模型
假定骨料为各向同性弹性材料,砂浆采用考虑塑性损伤耦合模型(concrete damaged plasticity,CDP)[9]。
对于砂浆而言,相应的应力-应变关系为:
(4)

Abaqus中内置CDP模型损伤变量的定义为:
1-d=(1-stdc)(1-scdt)
st,sc∈[0,1]
(5)
式中:st和sc是与应力状态相关的函数,表征应力反转所导致的刚度恢复效应;dc和dt分别是受压和受拉所导致的材料刚度退化。考虑到st和sc的表达式确定较为困难,本文中均取值为1。同时,本文不考虑循环加载工况,因此dt=0。经上述简化后,d=dc=dc(εp),即d只与材料的累积塑性应变相关,可通过单轴压缩试验确定。
采用Lubliner和Lee等提出的屈服准则:
(6)

对于准脆性材料,如岩石、混凝土和土而言,在破坏过程中会产生急剧的体积膨胀。为了反映这一现象,采用如下非关联流动法则:
(7)
式中:ζ为偏心率,本文中取默认值0.1;φ为膨胀角,取值范围为30°~40°,这里取下限值30°。
3 数值模拟
3.1 砂浆参数标定
在进行骨料模型分析前,需要对所用砂浆参数进行标定。试验在高刚性岩石力学试验系统(microsoft transaction server,MTS)液压伺服试验机上进行,采用位移加载的方式。所用砂浆采用C30混凝土,依据《混凝土结构设计规范(2015年版)》(GB 50010—2010),弹性模量取30 GPa,泊松比取0.15。另外,除上一节中提到的默认参数,其他相关参数通过拟合单轴压缩曲线获得。参数标定时,仅划分一个单元,类型为平面应变缩减积分单元CPE4R。相应的边界条件:A点固定支座,B点和D点采用滚轴支持,分别固定垂直向和水平向的位移(如图3所示)。位移加载量为0.005,即0.5%的应变。经反复试算,相应参数取值如表1所示,数值模拟曲线和试验曲线如图4所示。由数值模拟结果可知,所标定的参数可较好地反应材料峰前力学行为,对于峰后力学响应的预测则稍微偏大。
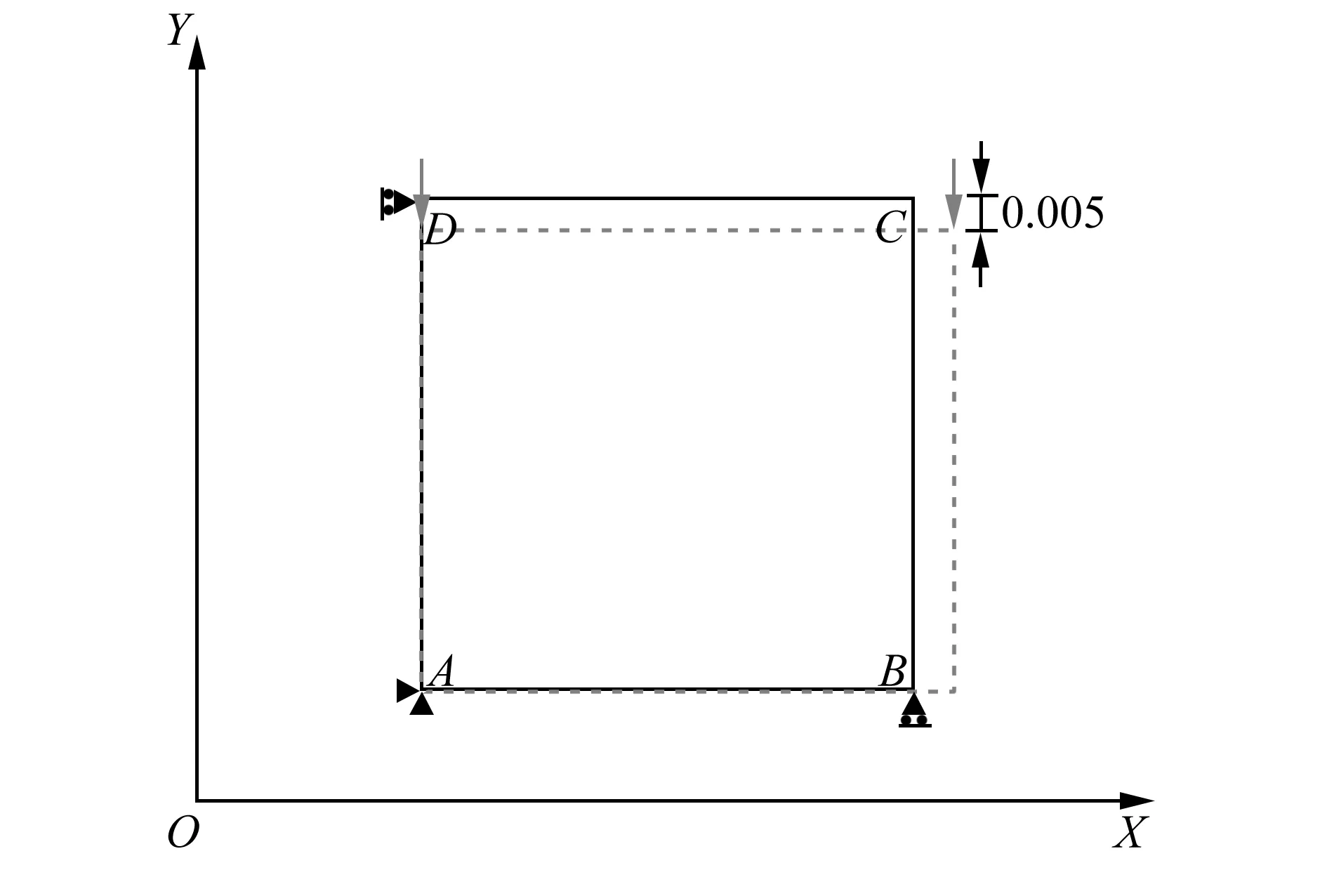
图3 本构模型验证示意图
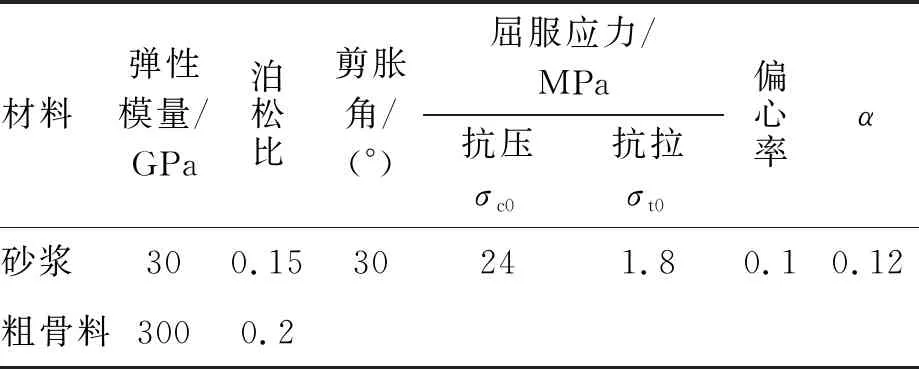
表1 各相材料的物理参数

图4 砂浆材料参数校核
3.2 数值模型
骨料采用三级配,最小骨料粒径和最大骨料粒径分别为5 mm和20 mm。当骨料体积分数为30%、35%和40%时,相应级配骨料的个数如表2所示。

表2 各相材料的物理指标
3.3 周期边界施加
在复合材料细观力学分析中,往往需要对选取的宏观代表性单元RVE(representation volume element)进行分析。为了增强计算效率和反映周边环境的影响,需要在RVE单元上赋予合理的边界条件,如式(8)所示[11]:
(8)
其中,U1,U2和U3和对应的加载条件相关。对于如图3所示的模型,其周期边界条件为:1)下边界为滚轴支撑;2)左右两侧的边界需保证在变形过程始终保持为垂直,为了达到这个目的,选取左上端部点为参考点,其余单元节点的变形与该参考点耦合。对右侧边的点进行同样的处理方式,使两侧边的变形在加载过程中始终保持一致。
3.4 平均力学性能
为了获取宏观的应力-应变响应,将相应的变量在空间进行平均,如式(9)所示:
(9)

3.5 计算结果
3.5.1 骨料质量分数的影响
构建三种不同骨料质量分数(30%,35%和40%)的模型,压缩应变为0.5%,鉴于CDP模型采用非关联流动法则,为了提高收敛速度,需要采用非对称求解器。应力-应变响应如图5所示,除40%骨料质量分数的模型外,另外两个骨料质量分数呈现明显的峰值和残余强度。同时,骨料的存在一定程度上改变了混凝土这类复合材料的受力性能。一方面,骨料质量分数的增加提高了混凝土的强度,另一方面,高骨料质量分数也改变了混凝土的变形模式。不同加载阶段破坏模式如图6所示,从等效塑性应变云图中可以看出,开始加载后,材料从初始状态逐渐进入损伤阶段,试件出现少量裂纹,裂纹扩展路径单一。随着加载的继续进行,沿加载方向上出现了更多的局部裂纹,裂纹逐步加粗加宽,最终试件发生破坏。而且,高骨料质量分数(40%)模型的破坏模式也较好地解释了应力-应变曲线中存在两个峰值强度的原因。第一个峰值由左下部的贯穿裂纹导致。由于夹具的约束作用,试样未完全丧失承载力。第一个峰值由右上部的局部裂纹导致。数值模拟结果表明,高骨料质量分数的混凝土试样易出现多条贯穿裂纹,而较低质量分数的骨料模型易于出现单一的贯穿裂纹。
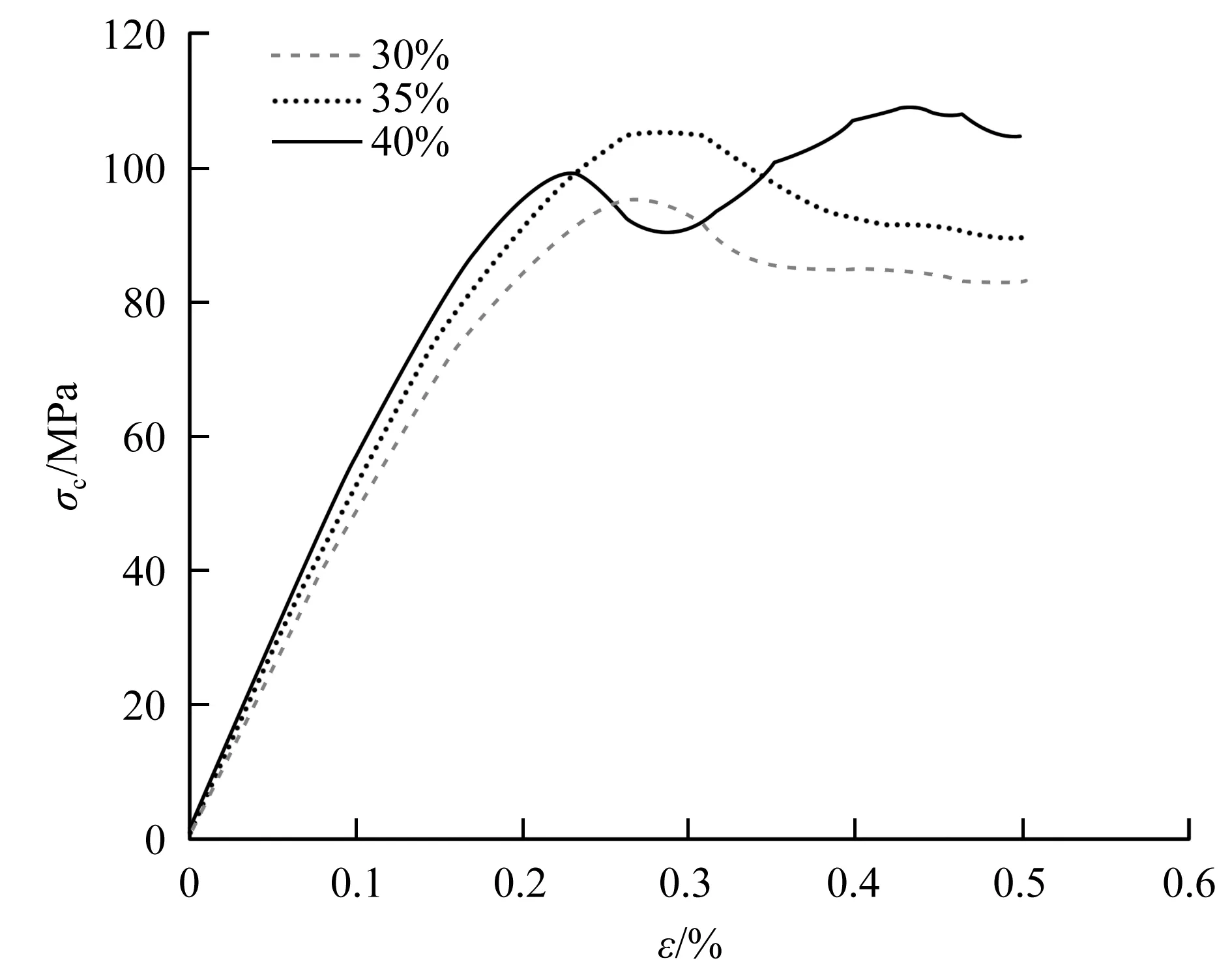
图5 不同骨料质量分数应力应变响应(单轴压缩)
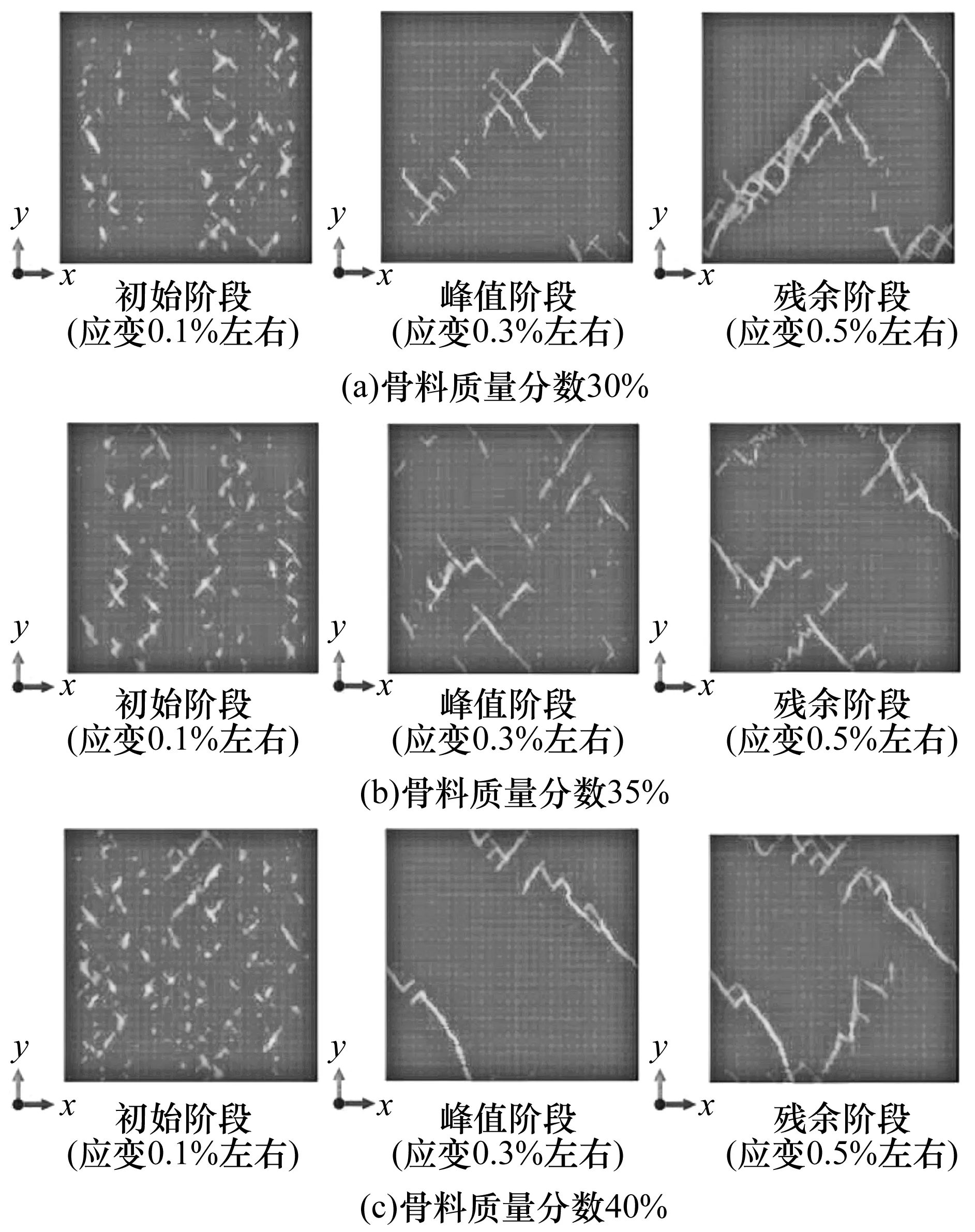
图6 不同加载阶段骨料模型破坏模式图
3.5.2 加载速率的影响
采用三种不同的加载速率(0.05 s-1、0.005 s-1和0.000 5 s-1)对骨料质量分数为30%的模型进行加载,相应的应力-应变曲线如图7所示。随着加载速率的减小,混凝土强度降低。同时,加载速率对混凝土最终破坏模式也有一定影响,如图8所示。数值模拟结果表明,低加载速率易出现多条贯穿裂纹,而高加载速率则倾向于产生单一贯穿裂纹。
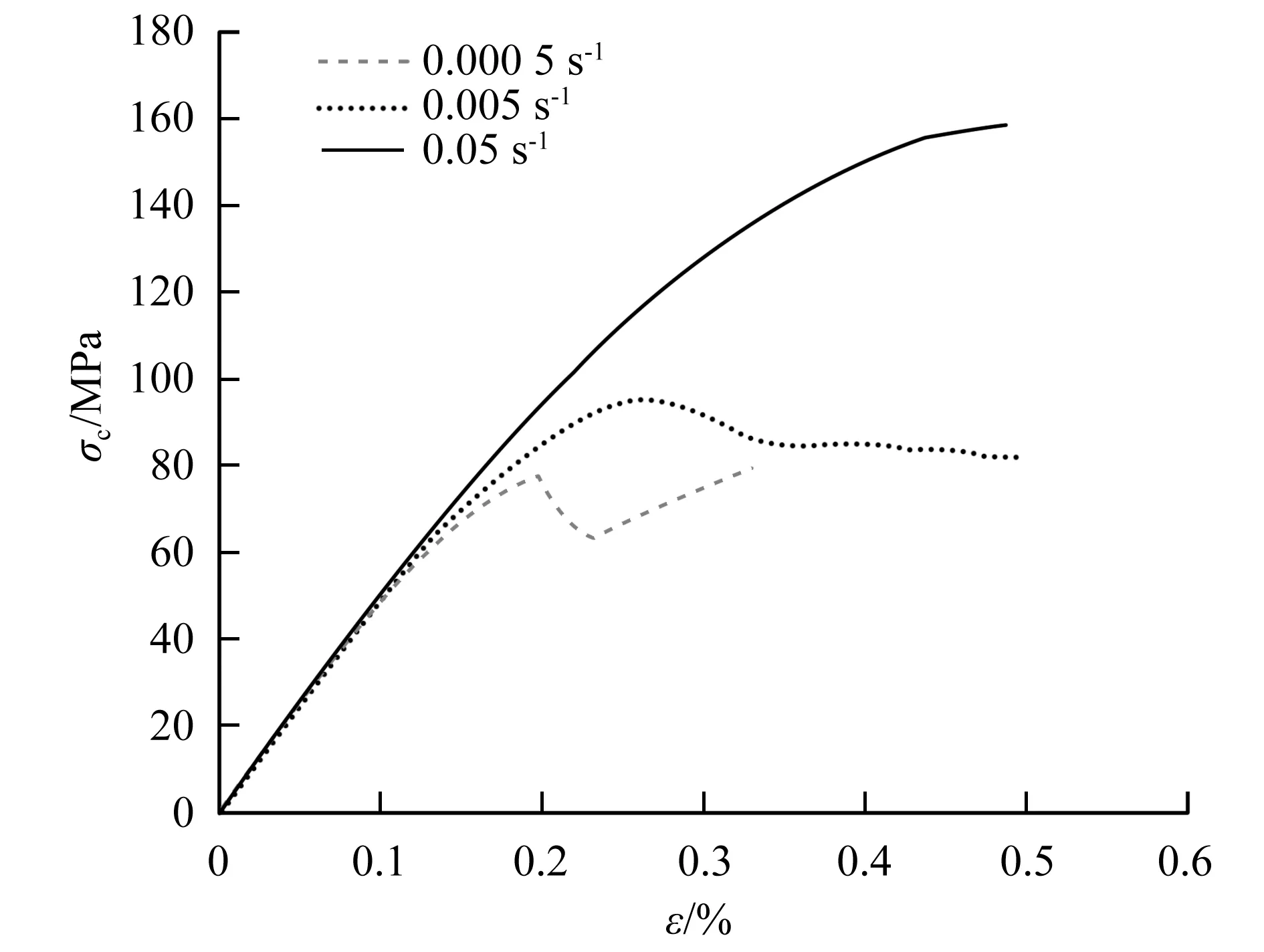
图7 不同加载速率应力应变响应(单轴压缩)

图8 不同加载速率骨料模型破坏模式图
6 结 论
CDP模型能很好地反映砂浆受压过程中性能劣化、裂纹发生发展的机制。随着荷载增大,试件中裂纹数量明显增多,裂纹走向趋于复杂。局部裂纹扩展逐渐形成贯穿裂纹最终导致混凝土失效。
骨料的存在一定程度上改变了砂浆这类准脆性材料的受力性能。一方面,骨料质量分数的增加提高了砂浆的强度,另一方面,高骨料质量分数也改变了混凝土的破坏模式。数值模拟结果表明,高骨料质量分数的混凝土试样易出现多条贯穿裂纹,而较低质量分数的骨料模型易于出现单一的贯穿裂纹。
随着加载速率的减小,混凝土强度降低。同时,加载速率对混凝土最终破坏模式也有一定影响。数值模拟结果表明,低加载速率易出现多条贯穿裂纹,而高加载速率则倾向于产生单一贯穿裂纹。
