尺规作图：以数学的方式建立命题———《三角形的三边关系》教学实践与思考

文|王平 郑文倩

【教学内容】

苏教版四年级下册第77、78 页。

【教前思考】

《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）在“三角形的三边关系”的学习内容中增加了尺规作图和运用几何基本事实“两点之间线段最短”进行推理的教学提示。尺规作图是直观几何向欧几里得几何过渡的重要桥梁，是学生感悟数学严谨性、增强几何直观和形成推理意识的重要载体。从第二学段起，2022年版课标对尺规作图的内容要求、学业要求、教学提示都有明晰的表述。教学中，一方面要启发学生在操作过程中思考三角形三条边的长度之间的关系，感悟命题“任意两边之和大于第三边”的意义，另一方面要引导学生用“两点之间线段最短”这个基本事实说明数学命题的正确性，形成推理意识。

【教学过程】

一、围绕图形要素，提出研究问题

师：通过昨天的学习，我们一起认识了三角形。我们都是从哪些方面认识三角形的，你对它们有了哪些认识？

生：我们是从顶点、边和角认识三角形的，知道了它们的数量，还有三个顶点的位置关系，不在一条直线上。

生：我还会画三角形。

师：能把三角形的特征整理一下吗？

课件出示表格：

图形要素 数量关系顶点3 个 3 个顶点不在一条直线上边3 条？角3 个？

师：观察他的整理成果，还有什么需要研究的问题吗？

生：三角形三个顶点有这样的关系，它的三条边和三个角有什么关系呢？

师：对呀，三角形的三条边是不是也存在着某种关系呢？具体说，是不是任意三条线段都能围成三角形？如果不是，有什么要求吗？（板书：三角形的三边关系）

【思考：三角形的学习贯穿于整个义务教育阶段的每个学段中，对它的要素研究是图形特征认识的起始。课始，教师通过提出回顾问题和整理要求将三边关系的研究置于三角形特征研究的完整背景里，帮助学生从顶点、边、角的维度进一步认识三角形，从而形成结构良好、角度清晰的认识，为后续学习其他几何图形提供研究方法和路径。】

二、借助尺规作图，发现一般规律

1.独立尝试，聚焦方法

课件出示：

师：选择一种，想办法围一围，再与同学交流。

师：我们从选择8cm、5cm、4cm 的先来交流，你们都是怎样围的，结果怎么样？

生：我选择用吸管搭一搭，结果围成了三角形。

生：我觉得吸管有点粗，可能不准确。我是在纸上画的线段。画成了三角形，画了好多次。（展示学生作品，如图1）

图1

师：的确画了很多次，其他同学也是这样吗？遇到了什么困难？

生：我先画8cm 的线段，第二条画5cm 的线段，然后去量最后这条线段两点之间的距离，有的时候长，有的时候短……

2.教师示范，讨论原理

师：看来用规定的三条线段画一个三角形并不简单，有没有好办法呢？

（学生沉思）

师：我像刚才几位同学一样，先画了一条8cm 的线段，并把线段的端点记为A 和B。（示范画图）

师：现在要找到一个点，它到A的距离是5cm，这样的点有很多，用什么工具可以帮助你找到？

生：圆规。

（教师演示，以A 为圆心，画半径是5cm 的弧）

师：那能找到很多点到B 点的距离是4cm 吗？（教师演示）有没有哪个点可以同时满足两个要求？

生：第一条弧上所有的点到A 的距离都是5cm，这条弧上所有的点到B 的距离都是4cm。它们相交的点到A 的距离等于5cm，到B 的距离等于4cm。

生：对啊，只要连接起来就成了一个边长是8cm、5cm、4cm 的三角形。（如图2）

图2

师：现在你能说一说像这样用直尺和圆规画图好在哪里吗？

生：它先画出符合两个条件的很多点，相交的点就同时满足两个条件。这样画图更加准确。

3.尺规作图，完善研究

师：比一比，你更喜欢哪种研究方法？把自己的研究完善一下。

师：哪位同学来汇报一下自己的画图过程和结果？

（呈现学生的画图成果，如图3，并在表格里板书数据和结果）

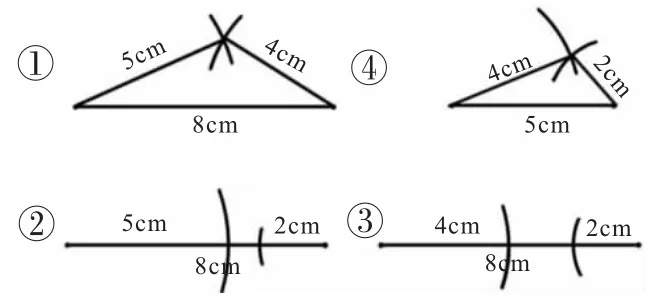
图3

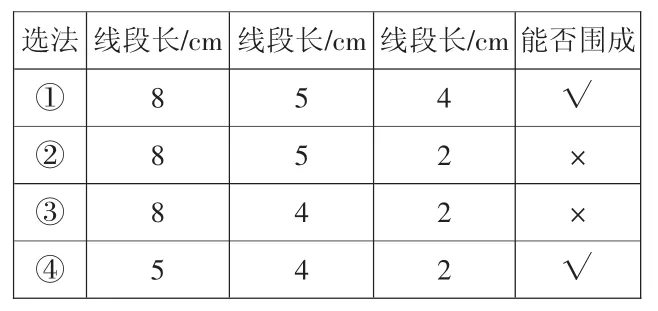
选法线段长/cm 线段长/cm 线段长/cm 能否围成①854√②852×③842×④542√

4.分析图形，探究规律

师：观察我们用直尺和圆规画出的图，①和④可以围成三角形，②和③不能围成，这是为什么？

生：从图上看，②和③画出的两条弧都没有交点，所以找不到满足两个条件的点，也就是找不到三角形的第三个顶点。

生：没有交点是因为两条线段太短了，不能首尾相接。比如②，5+2<8，两个长度还不满8cm，所以不能相交。

师：那么，反过来看，①和④可以围成三角形，它们任意两条线段长度的和与第三条线段的长度有什么关系？每次任意选择两条边算出长度的和，再与第三条边的长度比较，看看结果怎样。

（学生独立计算、比较）

师：你在每个三角形中是怎样算、怎样比的？

（板书算式和比较的结果）

师：从上面的比较中，你认为围成三角形的三条线段的长度间有什么关系？

生：任意两边的长度之和都比第三条边大。

师：如果三条线段的长度分别是8cm、5cm、3cm，能围成三角形吗？为什么？

生：我们想象一下，当两条线段长度的和等于第三条时，两条线段连接起来就和第三条线段重合，也不能围成三角形。

生：我画了图，是这样的（如图4），它们虽然相交了，但交点在原来的线段上，这样三个顶点就在同一条直线上了，所以不能围成。

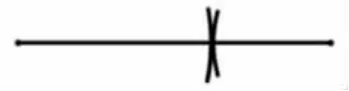
图4

师：现在你发现任意三条线段一定能围成三角形吗？那三角形的三边长度间的关系有什么特点？

生：三条线段的长度是有关系的，不是任意三条线段都能围成三角形。短的两条边要能在长的边外面搭起来，有交点。

生：随便哪两条边加起来都比剩下的边长。

生：也就是三角形任意两边长度的和大于第三边。

师：我们从不能围成三角形的线段长度与能围成三角形的线段长度的研究中发现，三角形任意两边长度的和大于第三边。

【思考：尺规作图引入前，教学中常用的方法是给学生提供吸管、小棒等有结构的材料进行实验，围出成果后再进行数据上的找规律，这样做也可以初步建立命题。由于实验材料的粗细等造成了较大的误差，课堂中教师通过想象尽量回避相差较小的数据，这给学生留下了疑问。借助尺规作图，教师可以将所有情况都画出来，在画的过程中学生就已经明白能否围成背后的原因，之后的数据分析就变成了对发现的数学表征，命题的建立过程更加直观确定。】

三、运用基本事实，形成数学命题

1.再认事实，建立联系

师：刚才的研究发现在生活中有哪些运用呢？这样的问题你们遇到过吗？（课件出示图5）

图5

生：从学校到少年宫有三条路线，中间的一条最近。

师：这是为什么呢？

生：我是把学校、电影院和少年宫看成三角形的三个顶点，根据今天我们研究得出的结论，三角形任意两边之和都大于第三条边，所以从学校到电影院再到少年宫一定比中间一条路线长。

生：同样的，从学校经邮局到少年宫也比中间一条长，所以从学校直接到少年宫的路线最短。

生：其实不用这样比，学校和少年宫是两个点，我们知道两点之间线段最短，所以中间路线比剩下的两条都短。

2.尝试推理，形成命题

师：刚才同学们用“两点之间线段最短”和“三角形任意两边之和都大于第三条边”说明了自己的想法，它们之间有联系吗？

生：根据“两点之间线段最短”，我们也可以得到“三角形任意两边之和都大于第三条边”。

生：（如图6）三角形中，边a是顶点A、B 之间的线段，而边b和c 是折线，所以它们肯定比a边要长一点。

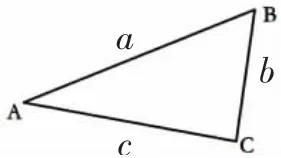
图6

生：同样的，边a 和b 的和一定比c 大，边a 和c 的和一定比b 大。

生：简单地说就是两点之间线段最短。

师：基于这个基本事实我们就可以推理了，你能不能用一个算式来表示两边之和大于第三边的结论？

生：AB 两点之间b+c>a；BC两点之间a+c>b；CA 两点之间a+b>c。

师：前面我们用直尺和圆规画图发现和验证，再经过用数学事实推理，反复验证它是一个正确的结论。今天这个反复被我们使用的结论叫什么？

生：三角形任意两边长度的和大于第三边。

【思考：三角形的三边关系的教学很多时候都仅限于根据学生的操作或数学实验的发现，对于数学命题的建立多是来自于不完全归纳，缺少数学推理的支撑，学生常常存疑。在学生的问题经过操作验证后，设计借助“两点之间线段最短”的数学事实，推理形成数学命题的活动，一方面有利于前后知识的融会贯通，发现数学知识是联系的，是可以生长的；另一方面有利于发展学生的推理意识，让学生体会到数学不只是来自于“看得见”的感性操作，更来自于“说得通”的理性推理。】

四、理解数学命题，拓宽生活应用

●水平一：解释——哪些线段可以围成三角形，为什么？（课件出示图7）

图7

师：你们是怎么想的？

生：只要最短的两条边的和与第三边进行比较就可以了。

师：第三组为什么不能围成三角形？

生：因为2+9＜15，所以围不成。

●水平二：阐明——还能画出哪些三角形？

师：围成的两个三角形之间有什么联系吗？

生：最长边都是10cm，另外两条边之和都是14cm。

师：像这样一条边是10cm，另外两条边的和是14cm 的三角形还有吗？

生：另外两条边可以是1cm和13cm，2cm 和12cm，3cm 和11cm，4cm 和10cm，5cm 和9cm。

生：不对，1cm 和13cm、2cm和12cm 不可以，因为1+10＜13，2+10=12，不符合任意两边之和大于第三边。

师：假设三角形的边长都是整厘米数，最短的边可以是几厘米？

生：最短的边是3 厘米。

●水平三：应用——还会形成什么图形？

师：如果边长不是整厘米数，三角形最短的边又可以是几厘米？

生：可能是2.1cm，还可能是2.01cm，只要比2cm 大都可以。

（教师使用几何画板，适时画出一条边是10cm，另外两条边的和是14cm 的三角形，如图8）

图8

师：想象一下，像这样画下去能画出多少个三角形？

生：无数个。

师：再想象，把这些三角形的第三个顶点连起来，会是一个什么样的图形呢？（如图9）

图9

师：三角形的三边关系与数学中的某些图形也是有联系的。

【思考：霍华德·加德纳认为，一个人能够将概念、原理和技能应用于解决新的问题和情境中，说明他充分掌握了这些内容。根据“理解六侧面”设计了三个水平的应用活动，分别检测“解释”“阐明”和“应用”水平，促进学生的理解进阶。过程中，学生通过对尺规作图原理的掌握，发现根据今天学习的内容，运用作图技能还可以创造出新的曲边图形。】

五、回顾探究过程，完善知识结构

师：回顾一下，我们是怎样研究三角形的三边关系的？你有哪些收获？

生：我学到了三角形任意两边之和必须大于第三边。

生：我们首先进行了猜想，三条边是不是像顶点那样有一定的关系，接着实验验证，再分析数据，最后根据以往学过的两点之间线段最短进行推理。

生：我还知道可以用直尺和圆规画三角形。

生：我对三角形的认识更完整了，我猜下面还会研究三角形三个角的关系。

【思考：三角形的认识是学生图形认识第一次由直观认识转入特征认识。本课结尾再次回归三角形认识的完整背景中，将对“边”的研究融入学生已有的认知结构。通过对过程和收获的回顾促使学生掌握知识的同时获得研究的维度和方法，为后续研究“角”以及其他图形提供可迁移的学习结构和方法结构。】