车载定位系统的应用及关键技术

2023-05-09蔡之骏李晓平

汽车实用技术 2023年8期

蔡之骏，张晔，李晓平

（广东省智能网联汽车创新中心有限公司，广州广东 511434）

随着通信技术及人工智能技术的发展，车联网及先进驾驶辅助系统（Advanced Driver Assistance System, ADAS）相关技术已逐渐普及，车用无线通信技术（Vehicle to Everything, V2X）等应用已在部分车辆上实现试运行或量产搭载，通过车联网实现车路人互联，可有效提高行车安全，优化交通状况[1-2]。然而，目前几乎所有的ADAS及自动驾驶场景均依赖于本车及远车的定位信息，车辆的定位精度会直接影响ADAS 及自动驾驶相关应用的准确度，定位偏差较大时，相关系统会发生误判，严重影响其功能的可靠性与准确性，在某些极端场景下甚至可能引起车祸。因此，作为整车定位信息的主要来源甚至是唯一来源，车载定位系统的作用与重要性也与日俱增[3]。

传统的车载定位系统一般使用单纯的卫星定位获取车辆定位信息，其成本低廉且易于实现，但其定位精度和稳定无法满足V2X 等ADAS 相关场景的应用（V2X 场景一般要求米级定位，若要与自动驾驶场景融合则需要分米级甚至厘米级定位）。因此，传统的车载定位系统在原有的卫星定位上逐步升级，加入差分定位、惯性导航及组合导航系统，以实现车载高精定位，满足ADAS 及自动驾驶的定位需求。

本文首先介绍了传统卫星定位的基本原理，然后分析在此基础上的主流车载高精定位方案及其原理。

1 卫星定位原理

传统的卫星定位也被称为全球导航卫星系统（Global Navigation Satellite System, GNSS）定位，其在车联网及自动驾驶相关需求出现之前是车载定位系统的主流配置。

在车载定位系统中，卫星定位的原理为车载定位终端直接接收包含原始观测量的卫星信号，然后根据收到的卫星信号，通过载波相位、码元等信息，解算出内部的距离信息。考虑到时钟误差的存在，理论上至少要同时能观测4 个卫星，才能计算出车载终端的位置信息，其方程组为[4]

式中，（xi,yi,zi）为每颗卫星各自的空间坐标，视为已知量；（x,y,z）为待求的整车定位结果；δtu为车载终端的时钟误差；ρi(i=1,2,3,4...)为车载终端接收到的来自可见卫星的伪距观测量，伪距定义为信号接收时间与信号发射时间之差乘以真空中的光速。解算上述方程组即可求出车载定位结果及时钟误差，从而实现整车定位与时间同步[5]。

由于观测误差与噪声的存在，定位终端一次接收到的卫星数量越多，理论上的定位效果也越好，每颗定位卫星都有隶属的卫星导航系统。当前GNSS 主要由以下四个卫星导航系统组成：全球定位系统（Global Positioning System,GPS）、格洛纳斯、伽利略与北斗，具体内容如下所述：

1）GPS 是在美国海军导航卫星系统的基础上发展起来的无线电导航定位系统，具有全能性、全球性、全天候、连续性和实时性的导航、定位和定时功能，现今共有在轨工作卫星31 颗，其中GPS-2A 卫星10 颗，GPS-2R 卫星12 颗，经现代化改进的带M 码信号的GPS-2R-M 和GPS-2F 卫星共9 颗。

2）格洛纳斯即全球卫星导航系统（Global Navigation Satellite System, GLONASS），是由原苏联国防部独立研制和控制的第二代军用卫星导航系统，该系统是继GPS 后的第二个全球卫星导航系统。GLONASS 系统由卫星、地面测控站和用户设备三部分组成，系统由21 颗工作星和3 颗备份星组成，分布于3 个轨道平面上，每个轨道面有8颗卫星，轨道高度为19 000 km，运行周期为675 min。

3）伽利略卫星导航系统（Galileo Satellite Navigation System, GSNS），是由欧盟研制和建立的全球卫星导航定位系统，该计划于1992 年2 月由欧洲委员会公布，并和欧空局共同负责。系统由30 颗卫星组成，其中27 颗工作星，3 颗备份星，卫星轨道高度为23 616 km，位于3 个倾角为56°的轨道平面内。

4）北斗卫星导航系统（BeiDou Navigation Satellite System, BDS）是中国自主研发、独立运行的全球卫星导航系统。我国正在实施北斗三号系统建设，已于2018 年底，完成19 颗卫星发射组网和基本系统建设，向全球提供服务；2020 年6 月已发射北斗三号最后一颗卫星，现已建成北斗全球系统，向全球提供服务；2035 年前还将建设完善更加泛在、更加融合、更加智能的综合时空体系。

2 差分定位

传统GNSS 定位实现简单，成本低廉，但其定位精度受诸多因素影响，例如：卫星信号穿过地球对流层、电离层时会发生折射，传播到建筑上会发生反射，这些都会导致信号传播时间计算有误，继而带来距离计算偏差，该误差可达几米甚至几十米。

为了消除这些误差，目前比较常用且有效的方法为采用差分定位，即在固定的位置建立若干固定的观测站，观测站也会同时观测卫星的信号，然后通过观测量建立误差的数学模型，再将差分改正数播发给定位终端，用以修正GNSS 定位过程中由于对流层、电离层等干扰带来的定位误差。定位终端根据收到的卫星观测量与差分改正数，通过算法即可获得高精度的定位结果，其中最常用的为动态差分技术（Real Time Kinetic, RTK）算法，使用双差模型，可使定位精度达到厘米级[6]。

RTK 算法基本原理如图1 所示，基准站r 和移动站u（在车载定位系统中，移动站即为车载定位终端）对卫星i 的载波相位观测值φr(i)与φu(i)可分别表示为

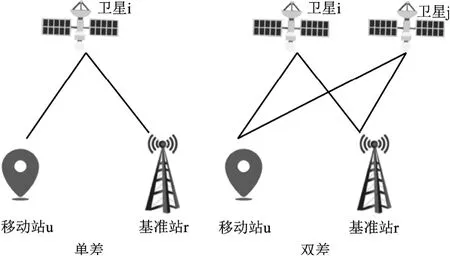
图1 差分定位原理图[6]

式中，λ为载波波长；和分别为基准站与移动站到卫星i 的几何距离；和分别为基准站与移动站的电离层延迟；和分别为基准站与移动站的对流层延迟；f为载波频率；和分别为基准站与移动站的接收机钟差； δt(i)为卫星钟差；和分别为基准站与移动站的整周模糊度；和分别为基准站与移动站的测量噪声。

将上述两式做差，可得

在短基线情况下，单差电离层与单差对流层延迟约等于0，故上式简化为

即为卫星i 的单差载波相位测量值。

同理，假设基准站r 和移动站u 同时跟踪观测卫星i 和卫星j，则

将卫星i 和卫星j 的单差测量值做一次差分，可得双差载波相位测量值为

其中，双差整周模糊度是未知整数，其求解是利用RTK 实现精密相对定位的关键，快速准确地求出整周模糊度的固定解能有效提升定位精度。整周模糊度需要使用在航模糊度解算（On The Fly,OTF）在动态情况下快速求解，目前普遍使用OTF中的最小二乘模糊度降相关平差法（Leastsquare AMBiguity Decorrelation Adjustment, LAMBDA）算法动态求解整周模糊度，该算法理论严密，搜索速度快，可满足相关需求[7-8]。

3 惯性导航系统

惯性导航系统（Inertia Navigation System,INS），简称惯导系统，主要包含导航计算机和惯性敏感元件。前者负责完成导航解算，后者包括陀螺仪和加速度计，其中陀螺仪输出方位角及载体角速度等相关信息，计算姿态矩阵，通过该矩阵将加速度计输出的载体加速度变换到导航坐标系，最后一起进行导航解算获取载体的位置、姿态和速度等惯导数据，整体流程如图2 所示。

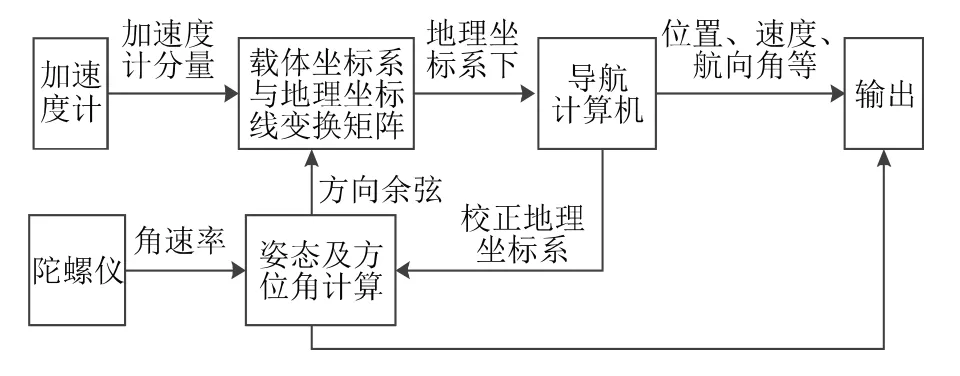
图2 惯性导航原理图[4]

与卫星定位及差分定位不同，惯性导航系统不需要卫星及网络信号就能定位。在车载定位系统中，惯导系统只需要来自整车的轮速大小及方向信息即能实现定位，在隧道等几乎没有卫星信号的场景下，车载定位系统需要依赖惯性导航系统继续保持整车定位输出，与此同时，惯导系统的定位误差会随着时间的积累而增加，在开阔场景等卫星信号有保障的场景下其性价比不如GNSS+RTK，因此，车载定位系统一般不会只选取惯导系统作为定位源。注意惯导敏感元件所输出的数据均基于载体坐标系，需要将其变换到求解导航参数较为方便的导航坐标系下，惯导系统常用的参考坐标系定义如下：

1.惯性坐标系

惯性坐标系（i 系）原点位于地球中心，在空间做匀速直线运动或处于静止，不参与地球自转，因此，也被称为空固坐标系。

2.地球坐标系

地球坐标系（e 系）原点同样位于地球中心，但其随地球一起自转，因此，也称为地固坐标系；其z轴指向地球北极，x轴指向参考子午面与赤道的交点，y轴为东京90°方向，且与x轴都在赤道平面内。

3.地理坐标系

地理坐标系（t 系）原点位于载体所处坐标，z轴与当地地垂线重合，x轴和y轴位于当地水平面内且分别平行于当地经线切线方向和纬线切线方向。

4.载体坐标系

载体坐标系（b 系）固定在载体上，原点位于载体质心，x轴沿载体横轴向右，y轴沿载体纵轴向前，z轴垂直于xy平面，构成右手坐标系（取法不唯一）。

5.导航坐标系

导航坐标系（n 系）也被称为当地地理坐标系，是惯导系统选取的作为导航基准的坐标系，一般使用地理坐标系作为导航坐标系，也可选用载体坐标系之外的其他坐标系。

4 组合导航

高精定位（GNSS+RTK）与惯导系统都有各自的优缺点与适宜场景：前者能在开阔场景下提供稳定的高精度定位，但在遮蔽环境（隧道等）下无法正常工作；后者则相反，能在遮蔽环境下稳定输出定位信息，但其误差随着时间累积导致无法保证长时间的定位精度。由于车辆实际的行驶环境错综复杂，不仅有隧道等完全遮挡场景，还存在着来自周边高架桥、高楼等各种临时遮挡，因此，目前越来越多的车厂开始在车载定位系统中使用组合导航方案，即使用高精定位与惯导系统进行组合，输出融合定位结果作为整车定位，单纯使用RTK 或惯导系统作为车载定位方案的厂家已经越来越少。根据高精定位数据与惯导数据耦合程度的不同，可划分为松耦合方案、紧耦合方案与深耦合（超紧耦合）方案[9]。

4.1 松耦合原理

松耦合中，高精定位与惯导系统各自独立工作，分别将各自的位置和速度等信息输出给车载定位系统中的滤波器（一般为卡尔曼滤波）进行融合定位，计算得出融合后的最优解并给惯导系统进行补偿反馈，如图3 所示。松耦合是高精定位和惯导系统的低水平层次组合，实现简单，但同时对卫星数的依赖较强，抗干扰能力与动态适应能力相对较差，即松耦合定位面对实际路况下的短遮挡场景，例如被测车辆旁边有大车经过时，定位结果会受到较大影响，导致定位结果不够稳定，具体测试情况参见4.4 节。

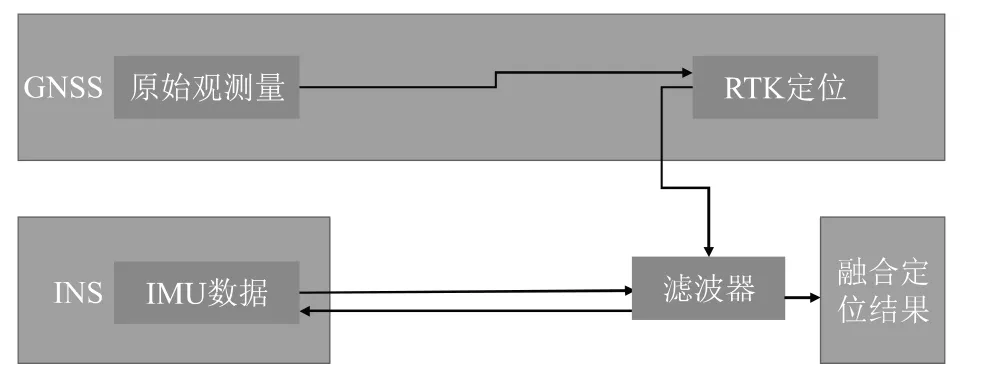
图3 松耦合原理图

4.2 紧耦合原理

与松耦合不同，紧耦合中惯导系统输出的惯导数据与来自GNSS 模组的原始观测量输入首个滤波器，结合惯导定位数据与GNSS 数据各自的置信度进行卡尔曼滤波处理，使数据按置信度进行整体排序并计算相应方差，过滤置信度偏低的数据，如图4 所示，同时，GNSS 原始数据与RTK后台下发的差分改正数据进行RTK 计算，获取经RTK 修正后的GNSS 数据，该GNSS 数据与首次滤波处理后的惯导数据及原始观测量数据三者一起输入给第二个卡尔曼滤波器进行二次滤波处理，同样按置信度进行排序、过滤并计算方差，算出的定位数据进行最终的滤波处理（以上每次滤波后都会给惯导系统进行反馈补偿），输出高精定位与惯导融合后的定位结果，即实现紧耦合组合导航方案。

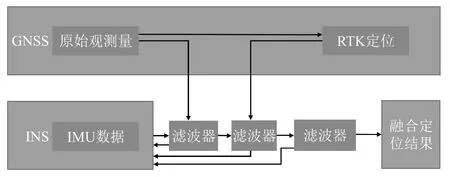
图4 紧耦合原理图

紧耦合方案相比松耦合有更高的定位精度，以及较强的抗干扰能力和动态适应能力，在带有较多短遮挡场景的路况下也能保持稳定的高质量定位（具体测试情况参见4.4 节），因此，被当前需要ADAS 及智能驾驶相关应用的车载定位系统作为主流方案使用。注意紧耦合方案需要惯导算法与差分定位算法有较好配合，对双方算法的要求都较高，因此，实现上比松耦合困难，成本也相对更高。

4.3 深耦合原理

深耦合则是在紧耦合的基础上，将惯导系统的部分数据直接送到基带芯片里，即惯性数据直接作为GNSS 解算的一部分，用来提高恶劣环境下载波相位、伪距等观测量的精度和连续性，减少观测量中断和跳变，从而进一步提高组合导航精度和可靠性。深耦合的结构决定其需要直接在基带模拟端进行融合，因此，实现深耦合方案，除了具备紧耦合算法能力外，还需要具备GNSS基带芯片模拟端接收能力，即只有自研基带芯片能力的公司才有做深耦合的能力。因此，目前仅有少数公司掌握该技术，应用较少[10]。

4.4 松耦合与紧耦合测试对比

上文所述松耦合与紧耦合为目前使用最多的两者组合导航方案，截取了部分量产实车路测数据以对比两者的差异。所对比的松耦合及紧耦合方案均采用双频RTK+惯导（惯导参数规格相同），天线为同一型号的车载鲨鱼鳍天线，测试路段相同。

测试结果对应的测试方法为量产实车搭载实际所用的车载定位系统，同时配备有国家资质认证的真值设备作为定位基准，在多条指定路段进行长时间往复行驶（平均速度≥50 km/h，每条路段每次测试时间为4 h 左右，路程200 km 左右），将车载定位数据与真值设备记录的定位数据对比，统计车载定位数据的圆概率（Circular Error Probable, CEP）误差。由于篇幅限制，测试结果中只选取最有代表性，也最常用的水平位置误差CEP95 作为判断。

松耦合绕城高速与机场高速的两次水平位置CEP95 相差都超过100%，如表1、表2 所示。经查证原因为第二次路测时路况较为拥堵，有大量卡车等大型车辆行驶导致车载定位系统的定位质量大幅下滑。反之紧耦合路测时也遇到了大量卡车拥堵场景，但其结果（表2）表明，紧耦合同一路段路测结果的水平位置CEP95 变化幅度远小于松耦合结果中CEP95 的变化幅度，原因为紧耦合方案动态适应能力更强，因此，定位结果相对更稳定，同时也能看出紧耦合方案的水平定位精度相对更高。