超声速飞行器近场声爆信号反演技术
2023-05-09黄江涛舒博文陈其盛高正红
马 创,黄江涛,*,刘 刚,陈 宪,舒博文,,陈其盛,高正红
(1.中国空气动力研究与发展中心,绵阳 621000;2.西北工业大学 航空学院,西安 710072)
0 引 言
声爆是超声速飞机飞行中特有的气动声学现象[1-2]。飞行器在超声速飞行时,其近场产生复杂的激波-膨胀波波系,这些波系传递到地面,形成空间内N形的声压分布[3],这就是声爆现象。声爆现象会对生物体和建筑物产生不良影响,因此早期的超声速客机只能在海洋上空进行超声速飞行。20世纪中后期,英法和苏联研制的以“协和”号和“图-144”为代表的第一代超声速客机都因声爆过强而被许多国家禁止在境内飞行[4],严重影响了其商业运营,最终以失败告终。声爆评估与抑制是超声速民机发展必须解决的卡脖子问题[5]。
声爆抑制涉及空气动力学与声学等多个学科,目前主要途径有流动控制(静音锥[5]、热流注入[6]、矢量发动机[7]等)、新概念低声爆布局(双向飞翼[8-9]布局、可变前掠翼布局[10]、双翼布局[11]等)、气动外形优化(代理优化[12-14]、梯度优化[15-17]、进化算法[18]等)……研究表明,在各类方法中,飞机气动外形设计是声爆抑制的最有效途径之一。其中,通过等效面积分布(equivalent area, EA)指导气动外形优化[19]是开展低声爆气动优化设计的一项关键技术。
等效面积分布是沿机身轴线的体积截面积分布与升力分布的叠加,直接决定了超声速飞行器的声爆特性,而飞行器等效面积分布特征较大程度由近场过压决定[20]。但是,通过近场过压反设计抑制远场声爆,缺乏直接的远场感知声压级作为指导。因此,探索有效的远场声爆信号向近场过压反演方法是开展声爆抑制研究的关键环节。
传统的低声爆反设计主要基于JSGD(Jones-Seebass-George-Darden)方法开展。20世纪70年代末,Jones、Seebass、George、Darden 四人[21-26]首次提出基于超声速线化理论的JSGD方法,为低声爆反设计奠定了理论基础。该方法在NASA的高速民用运输计划(high speed civil transport, HSCT)中得到广泛应用[27]。国内冯晓强等使用声爆预测算法与遗传算法对JSGD参数进行了优化[28]。但JSGD方法存在试凑的问题,且基于线化理论,对于复杂构型的计算误差较大,属于反向等效面积分布设计方法[29]。因此,有必要探索一种正向等效面积分布设计方法。
本文拟对近场声爆信号反演方法的“逆向传播+POD(proper orthogonal decomposition)”和“逆向传播+伴随方程”两种实现途径开展研究,以期为等效面积分布指导的超声速低声爆飞行器气动优化设计提供技术支持。
1 声爆信号的逆向传播
以零为初始值开始近场信号反演,无论是POD反演方法还是伴随方程反演方法,都将导致庞大的计算量,尤其对于POD方法,所需的样本空间极大。因此获取可靠的初始波形是进一步准确反演的关键。
远场声爆信号的逆向传播可以得到近场声爆信号大致波形,为进一步细节反演提供有力技术支撑。
1.1 声信号逆向传播模型
本文通过逆向增广Burgers方程来建立声爆信号的逆向传播模型。推导过程如下。
经典增广Burgers方程的无量纲形式为:
等号右端项依次对应声信号在大气中传播的非线性效应、经典耗散、非均匀介质和分子弛豫现象。式中:τ为无量纲时间,参考时间为1 / ω0,由近场声爆信号的采样频率决定;Γ为无量纲气体耗散系数; θv为无量纲分子松弛时间;Cv为无量纲松弛系数。
在经典增广Burgers方程中,几何扩散项和大气分层项取决于声管传播路径与面积,与时间相关的项只有非线性效应项、经典耗散项和分子弛豫项。建立逆向Burgers方程即对这几项进行修改,令时间反向流动[30]。
描述声信号逆向传播的逆向增广Burgers方程为:
1.2 逆向增广Burgers方程求解
逆向增广Burgers方程数值求解时,对过压信号进行时间离散,对声管传播路径进行空间离散,并对相关参量进行无量纲化处理。使用算子分裂法[31]对式(2)进行求解,可分裂成以下五项:
求解过程中,在当前高度依次更新无量纲压力P,空间推进直至目标高度,完成求解[32]。
式(3)可整理为如下形式:
式(9)~式(11)给出了式(8)的离散方法:
式(4)经典耗散项和式(5)分子弛豫项均为病态方程。为稳定求解,引入伪抛物线型正则化方法进行修正,修正形式如下:
依照工程经验选择 ε =1×10-4。引入式(12)所示的伪抛物型方程改写经典耗散项和分子弛豫项。
经典耗散项可以写成:
分子弛豫项可以写成:
其中,α取0.5。
改写后的经典耗散项和分子弛豫项均为三对角方程。使用TDMA方法[33]进行求解。
式(6)和式(7)为守恒方程,求解方法如下:
2 基于POD理论的声爆信号细节反演
由于正向传播与逆向传播均存在一定耗散,导致逆向传播结果中局部激波信号丢失,需要进一步对声爆信号进行精细化反演计算,以尽可能还原真实波形的细节。
本征正交分解是一种基于快照来描述高维空间的方法,其衍生的Gappy POD方法可进一步修复此高维空间内的任一残缺快照,因而可以用于反演近场声爆信号细节。
将设计好的目标远场波形作为残缺快照中的已知部分,待求的近场声爆信号作为残缺快照中的未知部分,通过对残缺快照的修复来实现对远场声爆信号的反演。
2.1 本征正交分解(POD)方法
POD本质上是一种降维方法。对于近远场样本组成的快照集 {Yi,i=(1,2,···,N)}(Yi∈Rn),POD可以从中寻找主要模态作为基模态使所有快照在各阶基模态组成的子空间上正交投影最大,表达式为:
然后,计算快照的脉动矩阵P:
采用奇异值分解(singular value decomposition, SVD)方法进行特征值分解。奇异值分解计算效率高于传统特征值分解方法,且在计算高阶模态时更精确。对矩阵P进行奇异值分解可得:
其中:U∈RN×N,V∈RN×N。 Λ ∈RN×n且仅有对角线元素Λii= σi(σ1≥ σ2≥ ···≥ σr≥0)非零,并得到各阶模态:
任意一个快照(如第i个)都可以由各阶模态的线性叠加得到,
定义各模态的能量为其对应的奇异值平方,
按照能量原则来选取基模态,定义能量下限为99.9%,即满足式(27)的前p阶模态被选择作为基模态。
2.2 Gappy POD方法
对于一个残缺样本,在POD的基础上发展出的Gappy POD方法可对其进行修复。对于一个如下形式的残缺样本
其中:K为样本中的已知元素,在本文中为远场声爆信号值;U为样本中的未知元素,在本文中为待求的相应近场声爆信号值。
POD方法提取出前p阶模态作为主模态,按以下形式给出:
基于最小二乘法,使用主模态对残缺样本中的残缺部分进行修复:
其中, Γ =(γ1,γ2···γL)T为残缺样本I在主模态张成的新的p维空间中的坐标。
修复得到的残缺样本中的缺失数据为:
2.3 声爆信号的“逆向传播+POD”反演方法
前文对POD理论的介绍也表明POD方法对样本空间的依赖性。由于超声速飞行器近场激波-膨胀波波系的存在,近场声爆信号波形大多呈现“N”形起伏。直接使用POD方法进行反演,对主模态的要求过于严苛,难以得到理想结果。
本文提出了逆向传播与POD结合的反演方法。首先进行声爆信号的逆向传播,得到近场声爆信号的波形主特征。以此为初始值进行POD计算,大大减少了POD的计算成本,仅需构造波形细节所需的样本空间,再对逆向传播的近场波形进行扰动取样即可。
采用“扰动取样—POD”迭代计算的方法进行反演,尽可能准确地还原声爆信号的局部激波。
3 基于伴随方程的声爆信号细节反演
基于声爆伴随方程求解梯度信息与差分方法相比,避免了大量重复进行Burgers方程求解的正计算过程,是一种高效的梯度求解方法,可基于逆向传播结果反演声爆信号细节。
将目标远场声爆信号视为目标函数,近场过压信号的每个时间离散点对应的过压值作为设计变量,以逆向传播得到的近场声爆信号为初始值进行梯度寻优,以得到更精细化的反演结果。
3.1 声爆伴随方程推导与梯度求解
将增广Burgers方程式(1)进行算子分裂后写成矩阵形式:
式(32)~式(35)分别对应氧气分子(O2)弛豫效应、氮气分子(N2)弛豫效应、经典耗散、非线性扭曲这四个声爆信号传播的物理环节。kn为增广Burgers方程式(1)右端第四项与第五项的乘积,表征几何扩散和大气分层对声爆信号幅值的影响。P、q、r、t分别表示求解过程中声压的四个中间值。
由上述矩阵形式,构造式(36)所示的拉格朗日量,推导声爆伴随方程的矩阵形式。
其中:l为目标函数;N为垂直空间网格数;D表示设计变量,即每个时间离散点对应的过压值; γ0、 γ1、β、λ分别为式(32)~式(35)表示的四个物理环节对应的伴随变量。
式(36)使用链式求导法则对设计变量D求导,可得:
令所有状态变量对设计变量的全导数为0,可以得到声爆伴随方程。
式(39)为声爆伴随方程,可进行迭代求解。将迭代结果代入式(38),可求得目标远场声爆信号对当前近场声爆信号设计变量的梯度信息。
3.2 声爆信号的“逆向传播+伴随方程”反演方法
绝大多数气动设计问题都可抽象为优化问题。本文的对声爆信号反演的研究,可视为如下所示的单变量最优化问题:
其中:Ftarget为目标远场过压信号;Ni为当前近场过压信号,以逆向传播所得的过压信号为初始值;FNi为 相应的远场过压信号;EM为欧氏距离;Ii为优化目标函数,只与当前一轮正计算的远场声爆信号有关。
通过求解声爆伴随方程更新目标函数对设计变量的梯度信息,基于序列二次规划算法进行梯度寻优,可得近场过压信号的反演结果。
4 基于LM1021标模的声爆信号反演技术验证
采用第二届声爆会议SBPW(the second sonic boom prediction workshop)提供的LM1021标模算例[34]对提出的方法进行可信度验证。LM1021外形示意于图1。
4.1 近场声爆信号与远场预测
在飞行器流场中,机身周向角0°的近场区域提取压力值,并计算得到过压值。近场过压信号在空间内的分布如图2所示。
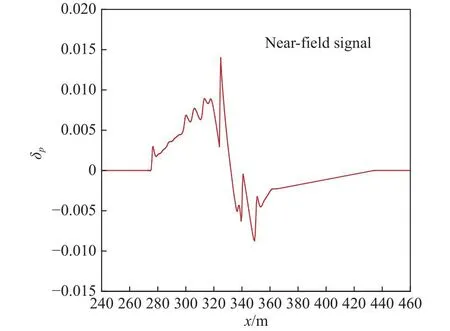
图2 近场声爆信号参考值Fig.2 Reference of near-field sonic boom signal
图3给出了声爆预测程序得到的远场声爆信号预测结果。由于预测程序中进行了时空变换,远场声爆信号为地面某一空间位置固定的观测点处的压力值随时间的变化。

图3 远场声爆信号参考值Fig.3 Reference of far-field sonic boom signal
本文提出的反演方法是对图3所示的远场声爆信号进行反演计算,使反演结果具有与图2所示的近场声爆信号等效的可信度。
4.2 远场声爆信号的逆向传播
基于逆向增广Burgers方程求解波形B的逆向传播结果,目标高度为飞行高度H= 16 747 m,声爆信号时间离散点数 ω0=50000。为了减少离散格式的数值耗散,垂直方向网格数为 5 0000。正则化参数ξ=1×10-6。
图4给出了逆向传播结果与真实近场过压分布的对比。经过逆向传播得到的波形,较为准确地反映了真实近场过压分布的主要特征。从图5中可以看出,仅经过逆向传播计算,近场声爆信号仍然存在较大误差,精度未达到设计要求。逆向传播误差较大部分主要由病态方程正则化造成,需要进一步对声爆反演信号进行精细化计算,以还原被耗散掉的细节。

图4 逆向传播结果Fig.4 Result of reverse propagation

图5 逆向传播结果相应的远场声爆信号Fig.5 Far-field wave corresponding to near-field wave of reverse propagation
4.3 声爆信号细节反演
声爆信号的细节反演采用两种方案,分别为POD反演方法与伴随方程反演方法,均以逆向传播的结果为初始值进行。
4.3.1 基于POD方法的声爆信号细节反演
首先将逆向传播得到的近场过压信号参数化,以定义设计域和控制变量。精细化反演计算的设计域为强激波区域,基于三次非均匀有理B样条(non uniform rational B-spline, NURBS)将设计域参数化,定义设计变量共80个,如图6所示。

图6 设计域与控制点分布Fig.6 Design area and control points distribution
逐个扰动控制变量,扰动量为 ± 0.001,扰动生成的每个近场样本都通过增广Burgers方程预测其对应的远场波形样本。一对相应的近、远场声爆信号样本组成完整的快照。图7给出了扰动生成的快照集。

图7 取样得到的快照集Fig.7 Sampling snapshots
通过POD方法可以得到从大到小排列的若干特征值和与之对应的模态。图8给出了前3阶模态形态。设定目标能量值为99.9%,经计算,前21个模态可以满足目标能量值的要求,可作为主模态来描述样本空间。建立包含目标远场声爆信号的残缺快照,使用GPOD方法修复。对上述“扰动取样-POD”过程迭代计算,残差定义同式(41)中的目标函数Ii,收敛条件为相邻迭代步的残差变化不超过1×10-5。共迭代400步收敛。

图8 POD得到的前3阶模态Fig.8 The first three POD modes
4.3.2 基于伴随方程的声爆信号细节反演
以逆向传播结果作为初始值,其时间离散点对应的过压值为设计变量,基于声爆伴随方程求解目标远场声爆信号对设计变量的梯度信息,并更新设计变量。使用序列二次规划(sequential quadratic programming,SQP)算法寻优,收敛条件为相邻迭代步的残差变化不超过 1×10-5。
4.3.3 结果分析
图9给出了两种反演方法得到的近场声爆信号。两种方法对主膨胀波前的声爆信号反演精度相当;对于主膨胀波后的声爆信号,“逆向传播+伴随方程梯度寻优”方法得到的结果有更真实的物理细节。

图9 反演结果Fig.9 Reverse results
经过细节反演得到的近场过压信号由增广Burgers方程可得相应的远场声爆信号,如图10所示。两种方法的可信度良好,在尾部激波区,“逆向传播+伴随方程”反演方法的结果与参考值高度一致,而POD方法存在一定偏差。

图10 远场声爆信号验证Fig.10 Far-field sonic boom signal verfication
远场声爆信号通过快速傅里叶变换(fast Fourier transform, FFT)得到频域内的声压级、响度级分布,如图11所示。图11表明,仅通过逆向传播得到的结果,相应的远场声压级与响度级信号在中高频区域误差较大,原因是声信号逆向传播中激波信号耗散严重,表明了使用POD方法与伴随方法还原波形细节的必要性。

图11 远场声爆信号的频域特征Fig.11 Frequency domain characteristics of far-field sonic boom signal
“逆向传播+伴随方程”方法的反演结果,其远场声压级与响度级高频信号精度优于“逆向传播+POD”方法。声爆信号的高频部分为激波,表明伴随方法对激波信号的反演能力优于POD方法。
本文提出的声爆反演方法旨在对人为设计的、达到适航要求的远场声爆信号进行反演,这一远场声爆信号主要参考感觉噪声级(preceived noise level, PNL)进行设计。感觉噪声级是根据三分之一倍频程声压级计算出来的表示人耳感觉到的噪声吵闹程度的单一数字[35],直接表征了声爆信号对人耳的噪声影响。反演方法的感觉噪声级精度验证如表1所示。
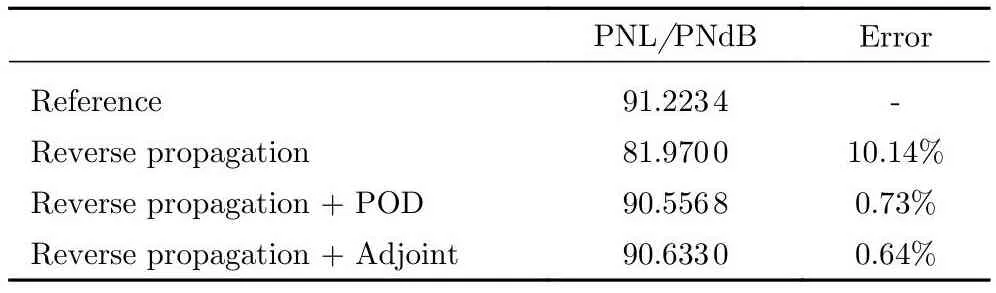
表1 感觉噪声级对比Table 1 Comparison of PNL
两种反演方法的感觉噪声级精度较逆向传播结果均有大幅提升,其中,“逆向传播+伴随方程”反演方法的精度高于“逆向传播+POD”反演方法。
4.4 等效面积分布分析
等效面积分布是飞行器声爆特性的决定性因素,因此也成为低声爆综合优化设计的指导函数。Abel算法可将近场声爆信号转化为飞行器的等效面积分布(EA),指导飞行器低声爆气动优化设计。其数学表达如式(42)所示。
图12给出了两种反演方法对应的等效面积分布,纵坐标为归一化处理的等效面积。相对于逆向传播结果,基于伴随方程反演得到的等效面积分布均更接近参考值,表明局部激波信号丢失对等效面积分布精度有一定不利影响,本文提出的声爆信号细节反演方法可有效降低这一影响。

图12 等效面积分布对比Fig.12 Comparison of equivalent area distribution
5 结 论
本文开展了“逆向传播+POD”与“逆向传播+伴随方程”两种超声速飞行器近场声爆信号反演方法的研究工作,验证了其在低声爆反设计优化中的可行性。该方法可进一步应用于未来超声速民机的低声爆设计,指导该类飞机的气动设计和优化。相关结论如下:
1)远场声爆信号频域内的声压级、响度级、感知声压级分析表明,仅经过逆向传播得到的近场声爆反演结果中局部激波信号丢失。而本文提出的两种声爆信号细节反演方法在逆向传播结果的基础上较好地还原了激波信号,感知声压级更精准。
2)尽管近场声爆信号波形存在一定误差,从远场声爆信号频域分析与人耳感知声压级分析结果来看,基于本文提出的方法开展远场声爆信号的设计、反演与飞行器气动外形优化设计是可行的。
3)声压级频域分析结果表明,伴随方程反演方法对声压中高频信号(即激波信号)的反演更精准,因此“逆向传播+伴随方程”声爆信号反演方法比“逆向传播+POD”声爆反演方法存在优势。
4)由反演结果得到的等效面积分布与参考值吻合度较好,表明两种反演方法能够为后续基于等效面积分布指导的优化设计工作提供有力支撑。
下一步将根据远场感知声压级设计声特性良好的远场声爆信号,基于本文提出的反演方法得到相应的近场声爆信号,进一步得到等效面积分布,开展低声爆伴随综合优化设计。
