基于平原河网模型的控制单元污染物允许排放量分配研究

周超 徐文文 王永泉 严天宇

（1.华设设计集团股份有限公司，江苏南京 210014；2.江苏省交通运输环境保护工程技术研究中心，江苏南京 210014）

1 引言

台州市黄岩区地处温黄平原，河网密布，是典型的平原河网地区。近年来，随着城镇规模的扩大、工农业生产的发展，水环境质量有所下降，成为制约黄岩区社会经济发展和人居环境质量提升的重要因素之一。目前，黄岩区的永宁江江口、东官河朱砂堆2处省控断面，南官河坝头闸、鉴洋湖2 处市控断面，现状水质已超过GB 3838—2002《地表水环境质量标准》Ⅴ类标准［1］。

现阶段国内多研究基于平原河网模型开展区域水环境整治［2-5］。本文根据河网概化原则建立了黄岩区平原河网数学模型，将研究范围内的黄岩区20条河流进行概化和水量水质计算，按照排污口概化原则，将所有污染源入河划分为40 个排污口，并进行水动力模型以及水质模型率定。基于上述基础，以典型河流永宁江为例，采用控制断面达标法得出永宁江流域2016 年最大允许排放量以及削减量目标，并根据允许入河量分配模型，得出各乡镇街道最大允许入河量及削减量目标，为精细化的区域水环境治理提供技术支撑。

2 研究方法

2.1 水动力方程

模型控制方程。描述明渠一维非恒定流的基本方程为一维Saint-Venant 方程组：

式中，q 为旁侧入流；Q，A，B，Z 分别为河道断面流量、过水面积、河宽和水位；Vx为旁侧入流流速在水流方向上的分量，一般可以近似为0；K 为流量模数，反映河道的实际过流能力；α 为动量校正系数，能够反映河道断面流速分布均匀性；x 为空间坐标；t 为时间坐标。

对上述方程组采用四点线性隐式格式进行离散。

2.2 水质方程

将平原河网区的河道概化为一维模型要素，其水质模型基本方程的守恒形式如下：

式中，C 为模拟物质的浓度；u 为河流平均流速；Ex为对流扩散系数；K 为模拟物质的一级衰减系数；x 为空间坐标；t 为时间坐标。

对流扩散系数是一个综合参数项，包含了分子扩散、湍流扩散以及剪切扩散效应。而在数值模型中，扩散系数除了与物理背景相关之外，还与计算空间大小、时间步长等相关。模型通过经验公式来估算对流扩散系数：

式中，V 是流速，来自水动力计算结果；a 和b 是设定的参数。

2.3 允许入河量分配模型

仅考虑自然条件差异，允许排放量公平分配模型数学表述如下：

式中，δ 为控制断面的最大允许增值浓度，δ＝Cs-Cb，其中Cs为控制断面控制浓度，Cb为控制断面背景浓度；ai为排污者i 对水质控制断面的污染贡献率；x～i为等贡献量分配结果；x¯i为平均分配结果；xi为排污者i 的允许排放量；m 为排污者个数；xiu为公平区间上限；xid为公平区间下限；ui为满意度，ui＝（xi-xid）/（xiu-xid）（xid＜xi＜xiu，i＝1，2，…，m）。

3 结果与讨论

3.1 模型建立

3.1.1 河网概化

为了模拟黄岩区河网水量水质的时空变化，进而为整个黄岩区污染物允许排放量计算提供科学依据，本文根据河网概化原则建立了黄岩区河网数学模型。对研究范围内的黄岩区20 条河流进行概化和水量水质计算，具体的概化情况见图1。

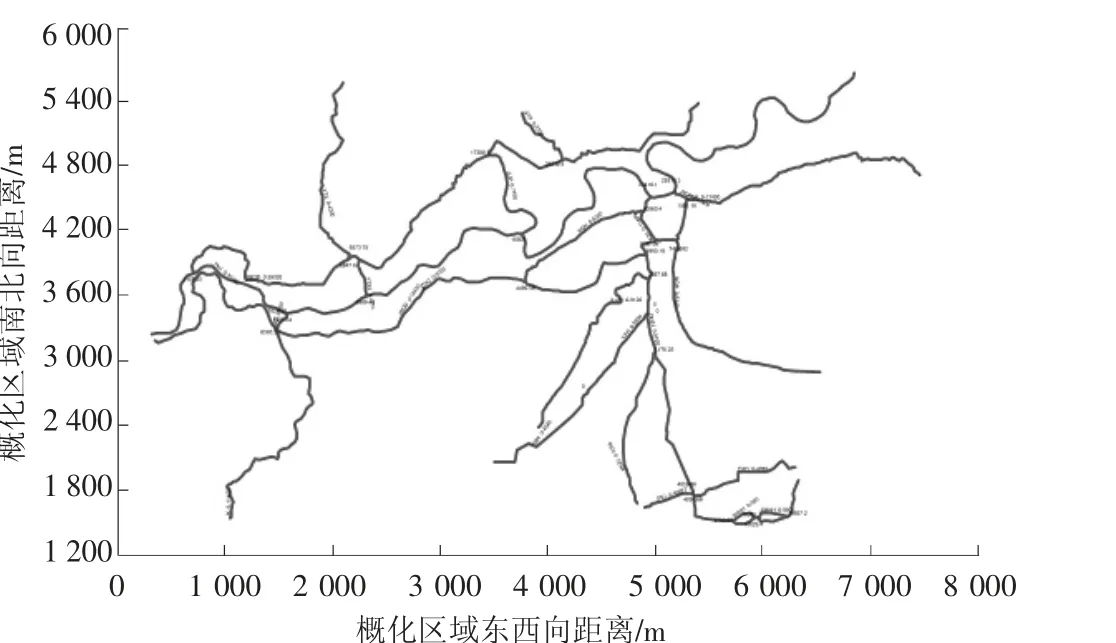
图1 黄岩区河网概化

3.1.2 边界条件

边界条件是河网数学模型的主要约束条件，本模型考虑了两种边界属性，分别为外部边界、内部边界。外部边界即开边界，是指控制计算区域内、外水体交换的约束条件，本模型共设置15 个开边界；内部边界是指模型计算范围内以点源或面源形式给出的排水口。

3.1.3 模型参数选取

（1）设计水文条件确定

根据长序列降雨量资料推求不同水文保证率的典型年，建立黄岩区主要水体的水量数学模型，本文以1963—2013 年50 年水文资料为基础，对连续50年的逐日降雨资料进行频率分析，得出黄岩区90%保证率下枯水年为1968 年，选取枯水年中对水环境不利时的入河流量作为设计水文条件，求出河道枯水年平均流量作为设计水量。河道属性、闸坝位置及调度方案等采用2014 年的现状工况。

（2）不均匀系数选取

河道越宽，污染物排入水体后达到均匀混合越难，不均匀系数就越小。一般性河流的不均匀系数取值范围见表1［6］。

表1 河流不均匀系数取值

（3）河道糙率及污染物降解系数选取

黄岩区水环境数学模型中河道糙率选取经验值为0.02～0.04。

利用一维稳态模型对水质降解系数进行求取，得出黄岩区氨氮降解系数取值为0.10～0.12 d-1，总磷降解系数取值为0.04～0.06 d-1。

3.1.4 排污口概化

按照排污口概化原则，根据研究范围内黄岩区各街道乡镇地形条件以及各类污染源的空间分布，将研究范围内黄岩区所有污染源入河划分为40 个排污口，其中，永宁江流域17 个、南官河流域13 个、东官河流域6 个、鉴洋湖流域4 个。

基于NMR测试混凝土微观结构的试验样本，为图2中随机切割下来的尺寸为40 mm×40 mm×40 mm的混凝土立方体，尽量保持样本中的粗骨料基本一致。图3为 NMR法测试微观结构的混凝土样本。

3.2 模型率定验证

3.2.1 水动力模型率定验证

采用坝头闸、黄沙闸、西江闸、永宁江闸2015 年全年监测资料对水动力模型进行率定，采用试错法（即根据部分断面实测的流量资料）调试各河道的糙率，使得计算水位过程与实测水位相吻合（见图2），率定得出河道糙率为0.021～0.039 之间。由水位误差分析结果可知，水位的相对误差均在10%以内，说明该模型可用于描述台州市黄岩区研究区域河网的水量变化过程。

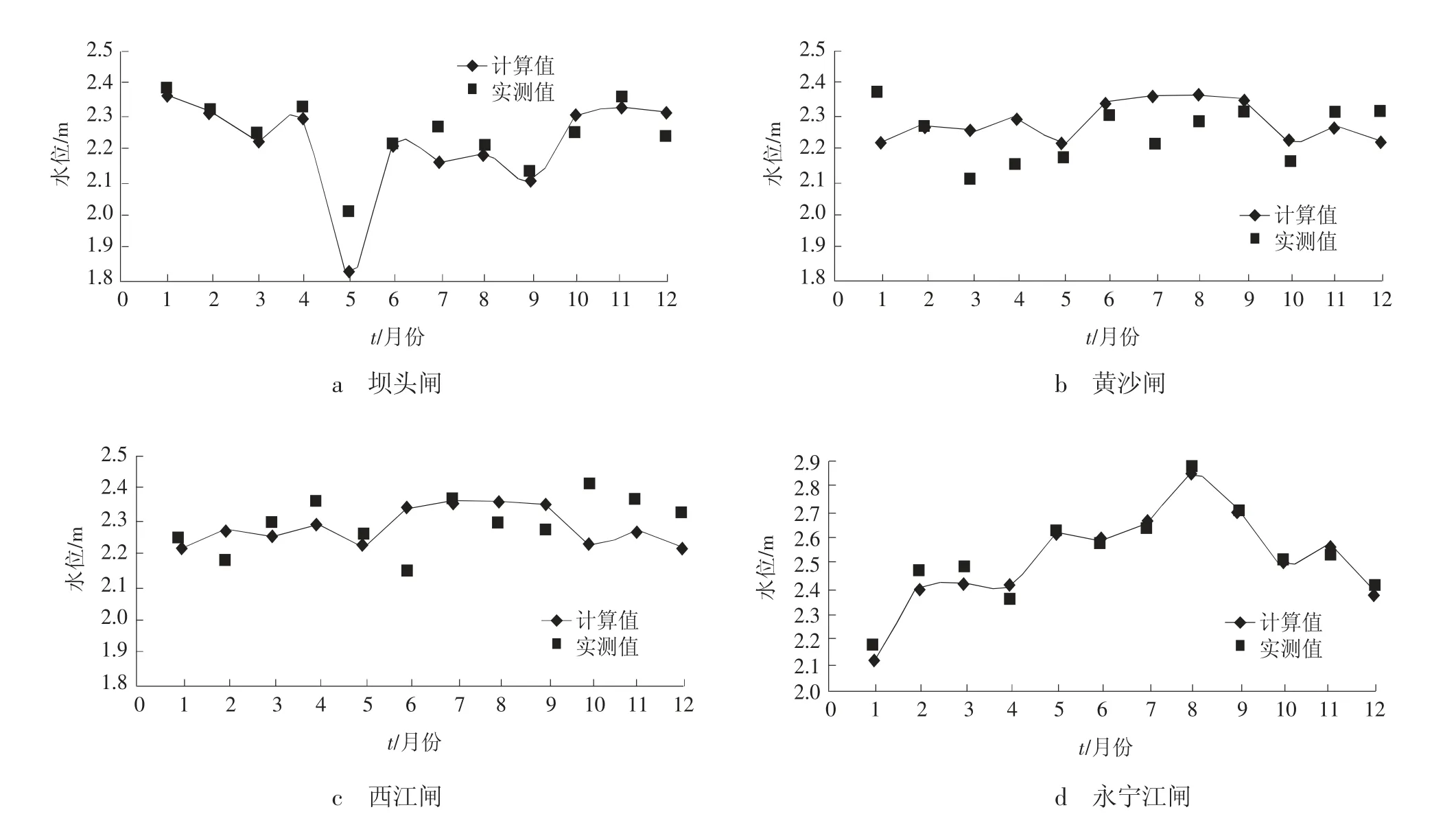
图2 2015 年研究区域4 个实测断面水位计算值与实测值率定

3.2.2 水质模型率定验证

根据台州市黄岩区环境监测站对朱砂堆、江口等4 个监测断面2015 年氨氮、总磷全年的监测结果，对水质模型进行率定。率定得到黄岩区氨氮、总磷降解系数分别为0.10～0.12 d-1，0.10～0.13 d-1。模型计算值与实测值的对比结果见图3。

图3 2015 年研究区域部分监测断面氨氮、总磷计算值与实测值率定

各断面的水质氨氮、总磷模型计算值与实测值吻合较好，相对误差分别在18.2%和18.6%以内，说明建立的水质模型适用于该地区的氨氮、总磷水质模拟。

3.3 控制单元污染物允许排放量的分配

3.3.1 最大允许排放量与削减量

表2 黄岩区永宁江流域规划年（2016 年）污染物最大允许排放量计算结果

3.3.2 允许入河量分配计算（1）污染贡献率的确定

根据建立的水环境计算模型，分别计算永宁江流域17 个排污口对江口断面的贡献率，结果见表3。由表3 可看出，污染贡献率的大小随距控制断面距离的减小而增大。

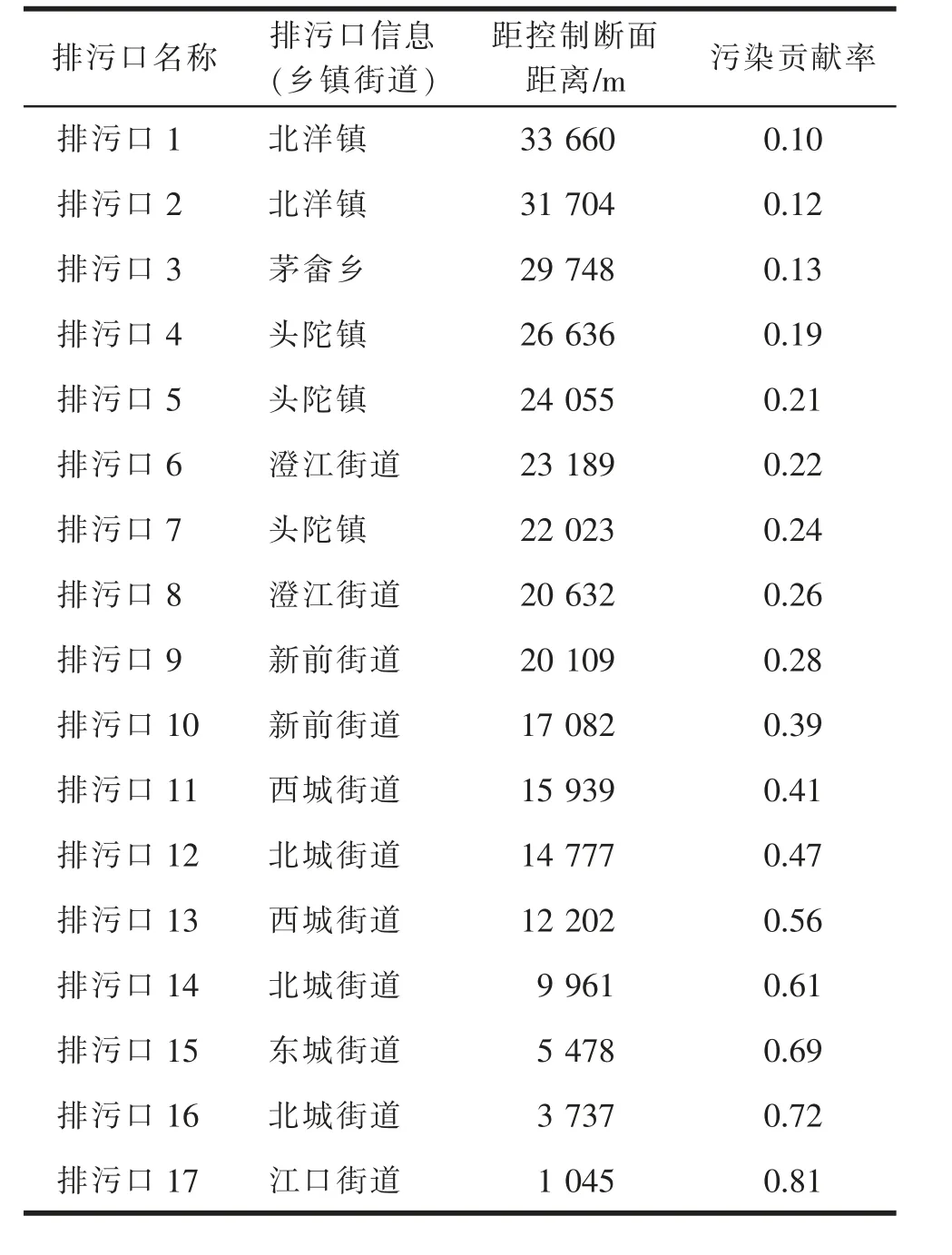
表3 黄岩区永宁江流域各排污单元污染贡献率

（2）允许入河量分配结果

根据允许入河量分配模型，求得各排污单元允许入河量，再根据所属乡镇街道进行合并，得出各乡镇街道最大允许入河量及削减量目标，见表4。由表4 可知，最大允许入河量以及削减量目标不仅分配到各排污单元，而且分配至各排污单位（乡镇街道）。

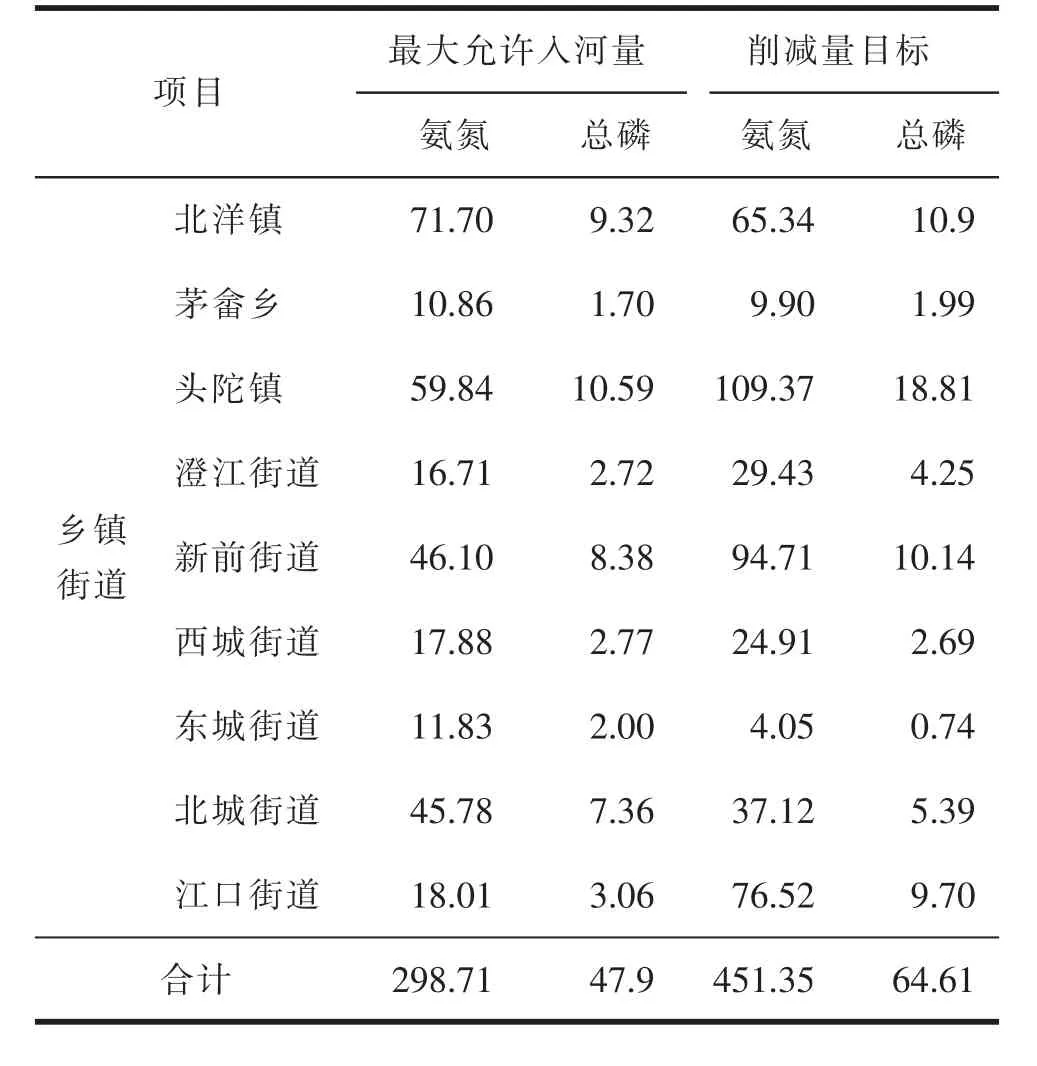
表4 黄岩区永宁江流域各排污单位允许入河量t/a

4 结论

以浙江省台州市黄岩区4 个控制断面所在河道为例，建立了该区域水环境数学模型，对模型进行率定验证，并以黄岩区永宁江为例，基于已建立的模型对研究区域的规划年最大允许入量进行计算并分配至各控制单元，从而指导区域水环境整治。

（1）根据断面流量资料对该模型的水动力模拟进行验证，水位的相对误差均在10%以内，说明该模型可用于描述台州市黄岩区研究区域河网的水量变化过程。

（2）根据断面水质监测结果对该模型的水质模拟进行验证，结果显示，各断面的水质氨氮、总磷模型计算值与实测值吻合较好，相对误差分别在18.2%和18.6%以内，说明该模型适用于该地区的氨氮、总磷水质模拟。

（3）以永宁江流域为例，通过平原河网模型分别计算永宁江流域17 个排污口对江口断面的贡献率，根据允许入河量分配模型，求得各排污单元允许入河量，再根据所属乡镇街道进行合并，得出各乡镇街道最大允许入河量及削减量目标，从而可有效地指导当地开展流域水环境整治。