穴盘苗补苗自动移栽路径规划优化研究
2023-05-08程方启
程方启
(浙江机电职业技术学院,浙江 杭州 310053)
0 引言
工厂化穴盘育苗技术已广泛应用于温室蔬菜种植,能够为蔬菜种植户提供健壮的蔬菜苗。在穴盘苗出厂前,需要用健壮苗替换那些缺苗或劣质苗。自动移栽机可提高穴盘苗的移栽效率和移栽品质、降低工人劳动强度和生产成本[1-3]。穴盘苗补苗的自动化移栽可描述为:自动移栽机的执行机构从供苗穴盘将健壮苗逐一取出,然后移栽到目标穴盘的多个待补苗的空穴孔中,在此过程中,自动移栽机末端执行器的总行程会因选择的取苗或补苗路径不同而不同。因此,对穴盘苗补苗自动移栽路径进行规划优化,可以有效降低末端执行器的行走距离,有利于提高补苗作业效率、补苗均匀一致性,节约运行时间[4-6]。
优化自动移栽机的移栽路径一直是该领域的研究热点[7-8]。童俊华等[9-10]采用标准遗传算法对穴盘苗补苗自动移栽的路径进行了研究,但其优化的算法设计模型与获得的结果有待改进。贺磊盈等[11]将贪心算法与遗传算法相结合对穴盘苗补苗移栽的路径进行优化研究,并与固定顺序法的计算结果相比较,结果表明该算法具有较好的效果。徐守江等[12-13]采用蚁群算法和混合蛙跳算法对穴盘苗移栽补苗路径进行了规划优化,研究结果与常规的固定顺序路径相比优化幅度较大,算法具有良好的稳定性。张丽娜[14]构建了免疫遗传算法与克隆选择算法2 种移栽路径的优化模型,并与固定顺序法和标准遗传算法做了比较,结果表明,基于免疫遗传算法的优化模型效率较高。尽管已有较多文献对穴盘苗补苗移栽路径进行了规划优化研究[15-16],但路径规划的设计采用算法的设计、效率及效果仍待提高。
1 穴盘苗补苗自动移栽问题描述与规划分析
常用的育苗钵盘尺寸一般为250 mm×500 mm,通常以穴孔数量G来定义其规格(其中G一般为25、50、72、128 等)[9]。穴盘苗补苗自动移栽系统中,补苗穴盘A 和供苗穴盘B 物理空间尺寸为630 mm×530 mm,补苗穴盘A 和供苗穴盘B 之间距离为100 mm,如图1 所示。穴盘格内小椭圆圈表示钵盘的穴苗位,供苗穴盘B 中黑色小椭圆圈表示不可取苗的穴苗位,其他小椭圆圈表示健壮穴苗;补苗穴盘A 中穴盘格内空白的表示待补苗的空穴位,其他小椭圆圈表示健壮穴苗。具体移苗过程描述如下:穴盘苗补苗自动移栽机的执行器从移栽系统的坐标原点出发,从供苗穴盘B 内取出1 株健壮苗移栽到补苗穴盘A 中的空穴孔内,不断循环直至补苗穴盘A 中的空穴孔全部完成补苗,之后再返回移栽系统坐标原点。穴盘苗补苗移栽路径规划的目的是确定往复移栽补苗的先后顺序,在末端执行器驱动速度一定的情况下最小化补栽路径长度,从而提高自动移栽机的工作效率。
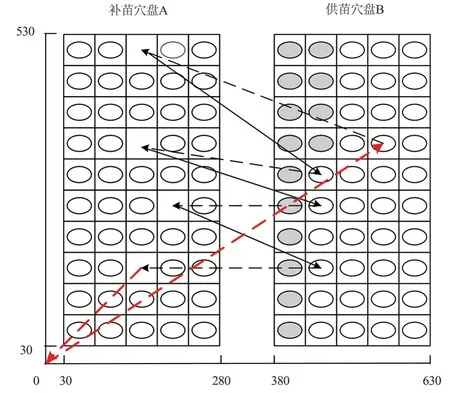
图1 钵盘补苗自动移栽作业示意图
假定A 盘需补种穴苗的空穴数量为k个,B 盘为可供移栽的健壮苗l株。在上述环境下,钵苗补苗自动移栽机末端执行器进行移栽作业时可选择的路径共有q种,计算公式为
式中:
k—— A 盘需补种穴苗的空穴数量,个,k≥1;
G—— A 盘的穴孔数量,个,l≤G;
l—— B 盘可供移栽的健壮苗,株,k≤l。
从公式(1)可看出,即使是小规模的问题,解空间也是非常大的。穴盘苗补苗自动移栽路径规划是一个典型的组合优化问题,也是一个NP(Nondeterministic Polynomial)完全问题,迄今没有一个多项式时间算法来解决这类问题,若采用遍历搜索算法来获得最短路径,则计算量巨大,难以满足补苗自动移栽机实时性的作业要求。本文尝试基于改进的遗传算法进行问题求解。
2 穴盘苗补苗自动移栽路径规划问题建模
2.1 定义穴苗位置与穴苗纵横方向顺序对应关系
以钵盘穴孔数为50 的规格为例,穴苗位置Pij与其坐标的对应关系见图2,设任一穴苗位置中心点坐标为Pij,其中,P表示穴苗位置,角标ij表示横坐标方向第i列、纵坐标方向第j行交点处的穴盘。其中,i,j均为自然整数,i=1,2,…,Nx,j=1,2,…,My;Nx为横坐标方向的钵盘A 与B 穴苗位置总数,My为纵坐标方向的钵盘A 与B 各自穴苗位置总数,图2中,Nx=My= 10。

图2 钵盘苗位置与坐标对应关系
2.2 穴盘苗补苗自动移栽路径规划模型构建
根据欧式定理,任意两点P1(x1,y1)与P2(x2,y2)之间的距离可表示为
式中:
x1——穴苗位置P1的横向坐标值;
x2——穴苗位置P2的横向坐标值;
y1——穴苗位置P1的纵向坐标值;
y2——穴苗位置P2的纵向坐标值。
设补苗穴盘A 有k个需要补苗的穴位孔,供苗穴盘有l个健壮穴苗可供移栽,则补苗自动移栽机末端执行器从坐标原点O 出发,依次从B 盘上将健壮苗移栽到A 盘的空穴位孔上,逐次完成第k个空穴位孔补苗后,从A 盘返回到坐标原点O。则补苗移栽路径行程顺序图可表示为
其中,O为坐标原点,Ai表示补苗穴盘A 的第i次补苗,Bi表示供苗穴盘B 的第i次取苗。整个移栽路径行程总长度可以表示为
式中:
PO—— 钵苗自动移栽机坐标原点位置;
G—— 钵盘穴位孔的数量,个;
k——A 盘空穴数,k≤G。
2.3 穴苗位置与坐标对应关系映射
在进行穴盘补苗自动移栽作业路径规划前,需要建立穴苗位置与坐标之间的对应关系,以便后续算法的编码与编程。采用直角坐标法与序号法相结合的编码方式,钵盘穴苗位置序号与其相对应的直角坐标互为映射关系[8],为了区分A、B 盘位置,设A 盘位置号为负数,B 盘位置号为正数,建立的钵盘穴苗位置序号如图3 所示。
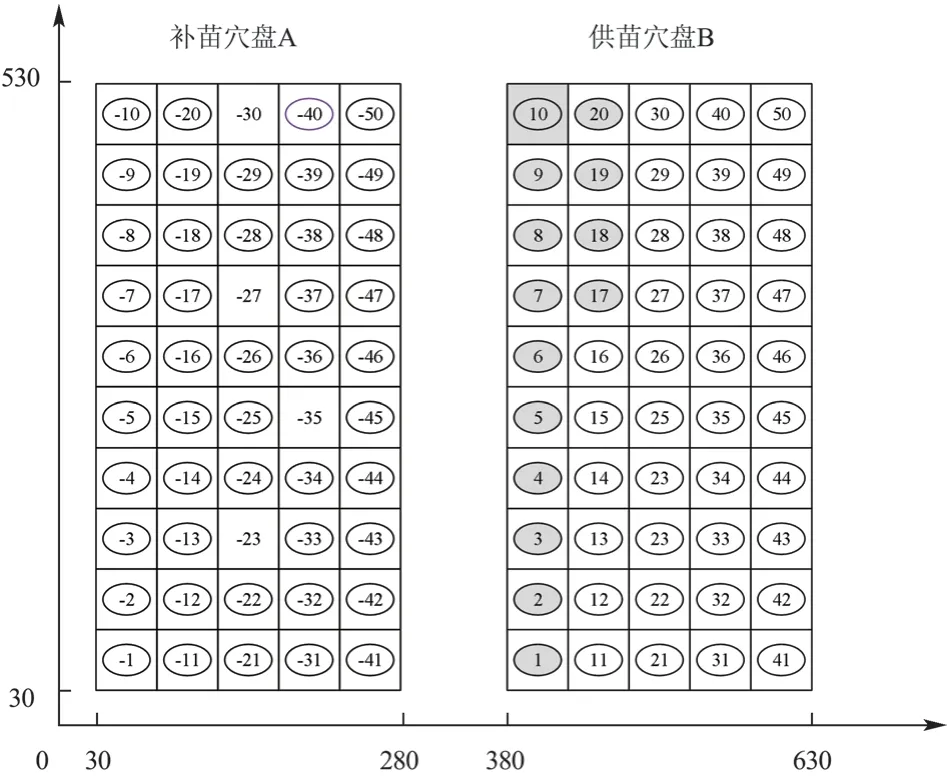
图3 钵盘苗位置序号图
以图3 为例,补苗穴盘A 中待补苗空穴孔为-23、-27、-30、-35;供苗穴盘B 中1~10 号和17~20 号共14 个穴位孔为缺苗或劣质苗(穴盘孔涂黑),其余为健壮苗。由于钵苗穴盘大小规格为250 mm×500 mm,根据补苗自动移栽机的布局与运动要求,A 盘左下角的位置坐标为(30,30),B 盘左下角的位置坐标为(380,30)。根据以上A、B盘的位置坐标信息,建立钵苗位置坐标与钵苗序号的映射。
对于补苗穴盘A,当穴苗位置序号P(i,j)≠-10,-20,-30,-40,-50时,穴苗位置坐标与穴苗序号的映射关系可表示为公式(4);当穴苗位置序号P(i,j)=-10,-20,-30,-40,-50时,穴苗位置坐标与穴苗序号的映射关系可表示为公式(5)。
对于供苗穴盘B,当穴苗位置序号P(i,j)≠10,20,30,40,50时,穴苗位置坐标与穴苗序号的映射关系可表示为公式(6);当钵苗位置序号P(i,j)=10,20,30,40,50时,穴苗位置坐标与穴苗序号的映射关系可表示为公式(7)。
式(4)—(7)中:
X(i,j)——(i,j)位置处的横向坐标值;
Y(i,j)——(i,j)位置处的纵向坐标值;
P(i,j)——(i,j)位置处的穴苗位置序号;
i和j均为介于1~10 之间的整数,mod 为求余运算;floor 为向下取整运算。
3 穴盘苗补苗移栽路径优化的遗传算法设计
3.1 遗传算法的编码机制
前述已将钵盘穴苗位置映射为序号,A 盘符号为负数,B 盘序号为正数。根据补苗移栽路径行程顺序图可知,可将染色体定义为由坐标原点与穴苗位置序号构成的线性数字序列,如表1 所示。设k=4,l=36,则随机列出一条染色体编码(0,32,-27,16,-35,23,-30,24,-23,0)。由表1 可见,染色体长度为2k+2,即取决于待补苗的空穴数量。染色体对应的路径行程长度S由2k+1 段两点间距离的总和。

表1 染色体编码机制说明
3.2 构造适应度函数
适应度函数值是评价一条染色体好坏的依据,会对计算结果带来直接的影响。参照公式(3),S表示补苗移栽行程总长度(目标函数),在遗传算法中适应度值是越大越好。本文令染色体ζ的适应度函数为f(ζ),在任一个种群的所有路径中,必然存在最大值Smax与最小值Smin,考虑使总长度最短的路径适应性为1,而最长路径适应性为0,其他路径则介于0~1。适应度函数可表示为
式中:
f(ζ)—— 染色体ζ的适应度函数;
Sζ—— 染色体ζ的路径行程长度值;
Smax—— 所有染色体遍历后路径行程中的最大值;
Smin—— 所有染色体遍历后路径行程中的最小值。
3.3 遗传算子的改进机制
选择、交叉和变异等遗传算子的操作都会直接影响遗传算法的效率和收敛速度,而穴苗补苗自动移栽路径规划需要在进行算法设计时对遗传算子进行改进操作。
3.3.1 选择操作
采用轮盘赌法进行遗传算子的选择操作,适应度值越大的个体被选中的概率越大。每个个体的适应度除以总适应度值,以此作为每个个体的被选中的概率。以初始种群数为父代、个体选择概率为选择依据,计算适应度值并按照由大到小对相应个体进行排序。
3.3.2 交叉操作
对初始种群选择操作完后,进行交叉的遗传算子操作。因自动移栽路径编码分别对应于2 个穴盘内钵苗的不同基因位置标记且具有唯一性,因此,要求交叉后各基因位置的元素不能相同。基于此,以补苗穴盘有4 个待补苗空穴孔,供苗穴盘有36 个健康苗穴孔为例,其补苗移栽路径的交叉策略描述如下:
1)随机选择种群中的偶数条染色体,确保两两相互交叉操作。随机产生2 个2~7 之间的自然数i和j,确保从染色体基因位第3 位才开始交叉操作,若从第2 位开始交叉且步长等于9,则相当于种群中2 条染色体互换位置,起不到使种群多样化的目的。其中i为染色体基因位,j为交叉步长。如i+j≥9,则令i+j= 9,染色体基因最后1 位为原点,不需要参加交叉操作,既保证交叉不超出染色体长度,又减少了最后1 位的无效交叉,提高运算效率。
2)以i= 3,j= 4 为例,图4(a)中,染色体Ⅰ和Ⅱ交叉操作,染色体Ⅰ的第4~7 基因位片段(-35,23,-30,24)与染色体Ⅱ对应的第4~7 基因位片段(-30,35,-27,14)片段交换,形成新的染色体,如图4(b)所示。
3)检查同一染色体中基因位是否存在相同的序号,如有,则用100 代替。交叉后形成的新染色体Ⅰ不存在重复的序号,而交叉后形成的染色体Ⅱ第2与第8 个基因位元素相同(均为24)、第7 与第9 个基因位元素相同(均为-30),如图4(c)所示。将交叉后染色体Ⅱ的第2、7、8、9 四个基因位的元素替换为100,如图4(d)所示。
4)遍历染色体2~9 基因位,用有效元素代替100。如图4(e)所示,当100 所在基因位为奇数时,表示这些元素来自补苗穴盘A,即(-23,-27,-30,-35)。经遍历后发现(-23,-35)两个元素已使用,则第7 基因位随机从(-27,-30)中选1 个元素(如-30),剩余的另1 个元素放在第9 基因位(-27)。当100 所在基因位为偶数时,表示这些元素来自供苗穴盘B,即11~16 和21~50 等元素。经遍历后发现(30,35)两个元素已使用,则第2 基因位随机从11~16 与21~50(30,35 除外)中选1 个元素(如45),剩余的另1 个元素放在第8 基因位(-27)。最终得到交叉后新的染色体Ⅰ和Ⅱ,如图4(f)所示。

图4 交叉操作机制
3.3.3 变异操作
为了使种群保持多样性,避免陷入局部最优,采用遗传算子的变异操作。考虑到补苗自动移栽路径的双盘基因位的相异性,确保变异后个体的有效性,变异操作需要采取单点变异与元素替换相结合的策略,对变异算法描述如下:
1)随机选择种群中的数条染色体进行单点变异操作。随机产生1 个2~9 之间的数i,确定该染色体变异操作的基因位。判断该基因位的元素为正数或是负数,从而确定是奇数基因位还是偶数基因位。
2)若为奇数基因位,则需从补苗穴盘A 中选择元素。如图5(a)所示,随机数i=5,该基因位现有元素为-35,则可以变异为(-23,-27,-30)中的任一元素。假设该基因位元素-35 随机变异为-27,则遍历奇数基因位,将元素-35 替代原-27 元素所处的第9 基因位,从而得到变异以后的新染色体,如图5(b)所示。
3)若为偶数基因位,则需从供苗穴盘B 中选择元素。随机数i=6,该基因位现有元素为21。变异存在2 种情形,当该基因位元素21 变异为11~16 与21~50 的任一元素且不等于19,38 或16,此时得到新染色体I-1,此为变异情形1,如图5(c)所示。当该基因位元素21 变异为19,38 或16 中的任一元素时,如变异为19,那么该元素与第2 基因位元素值相同。此时,需要将原来变异前的元素21 替换第2 基因位的元素,得到新的染色体I-2,此为变异情形2,如图5(d)所示。
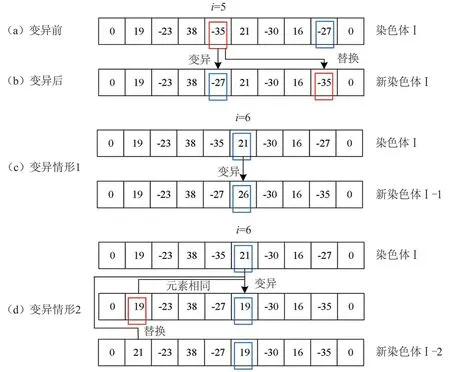
图5 变异操作机制
3.4 最优染色体保存与最差染色体替换策略
为有效防止遗传算法陷入“早熟收敛”,可采用最优染色体保存策略,如图6 所示:①生成种群后计算适应度值,找出最优染色体(最优个体)并保存。②找出经选择、交叉、变异操作后新种群中的最优个体。若本代最优个体优于上一代最优个体,则用本代最优个体代替上一代最优个体,同时,用次优个体代替本代的最差个体。若本代最优个体差于上一代最优个体,则保存上一代最优个体,同时,用本代最优个体代替最差个体。③继续循环迭代至迭代完成。最优的个体不参与交叉、变异操作,可以确保最优的个体可以遗传到下一代。利用每次迭代中新种群的次优或者最优个体代替最差个体,可以提高种群的多样化,不陷入局部收敛,提高运算速度。

图6 最优个体保存策略算法流程
4 仿真试验与结果分析
根据上述算法模型对穴盘苗补苗自动移栽路径进行规划优化,由于穴盘规格和空穴数量的不同对算法设计不会产生影响,分别设计有效性仿真试验和随机性对比仿真试验。仿真环境为MATLAB R2018a,该算法运行平台为Thinkpad 笔记本电脑,处理器为Intel(R)Core(TM)i7-10510U CPU,RAM 为16.0 GB。
4.1 有效性仿真试验与结果对比分析
以图1 补苗移栽作业要求为例进行优化计算[9,12]。交叉概率、变异概率分别取0.8 和0.3,种群规模为20,优化迭代次数为200。
通过改进的遗传算法求解,以钵苗移栽路径总长度为目标的函数曲线收敛很快,其中一次计算如图7 所示,经过72 次迭代,得到路径总长度最小值为2 913.892 009 983 26 mm,保留到个位数,记为2 914 mm,平均优化算法运行时间0.43 s。图8中箭头所示路径为经优化后的最优移钵路径解(0,13,-35,15,-30,16,-27,14,-23,0)。本文的算例初始参数设定参考童俊华[9]和徐守江[12]的研究,经算法运行后获得路径长度和最优路径,如表2 所示。本文算法Ⅰ经与童俊华[9]和徐守江[12]的研究对比后可以看出,算法Ⅰ与算法Ⅱ均可获得最优路径长度为2 914 mm,算法Ⅲ获得的最优路径长度为2 930 mm,说明算法Ⅲ获得的最优补苗移栽路径解(0,12,-35,15,-30,16,-27,14,-23,0)不是该问题的最优解,而是该问题的1 个次优解。本文设计的算法Ⅰ比算法Ⅲ获得的最优路径长度缩减了165 mm,缩减幅度为5.6%。对比3 种算法获得最优路径可以看出,算法Ⅲ路径中选择的第2 个基因位的元素为12,而算法Ⅰ与算法选择的第2 个基因位为13,其余基因位元素均相同。
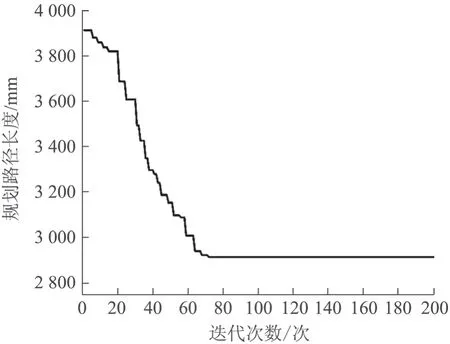
图7 路径长度收敛变化曲线
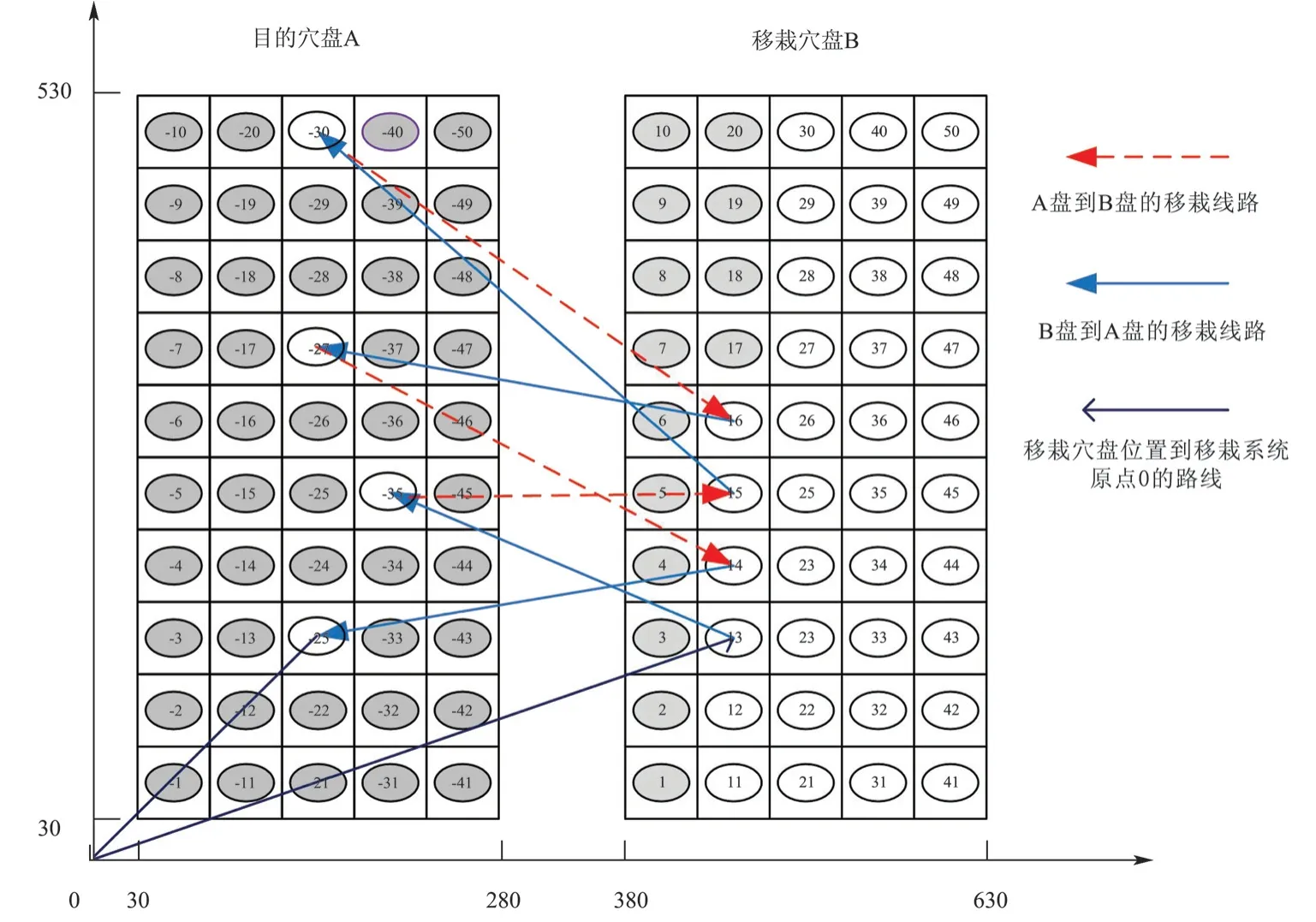
图8 经优化计算后获得的最优路径(总长度2 914 mm)

表2 不同算法效果对比
4.2 随机性仿真试验与结果分析
为了进一步分析本文算法模型的效率,选取规格为50 穴孔钵盘进行移栽路径规划仿真试验。补苗穴孔数量分别设为4、5、6、7、8,补苗穴孔位置随机确定。供苗穴孔数量对应分别设定为36、42、39、43、41,取苗穴孔的位置随机确定。每组做5 次试验,路程长度与运算时间均取5 次试验的均值。随机性仿真试验初始参数如表3 所示。

表3 随机性仿真试验
经仿真试验,按试验组别获得的路径规划长度均值分别为2 914、3 340、3 824、4 249、4 851 mm,如图9 所示。路径长度受补苗穴孔数量、取苗穴孔位置和补苗穴孔位置等因素的影响,整体趋势上看,随着补苗穴孔数量的增多,移栽路径长度均值也逐渐变大。按试验组别获得的运算时间分别为0.43、0.45、0.46、0.49 和0.49 s,从整体趋势上看,随着补苗穴孔数的增大,染色体基因位也增多,路径长度也变大,运算时间也逐渐变大,如图10 所示。

图9 多组试验下补苗穴孔数量与路径长度均值的关系
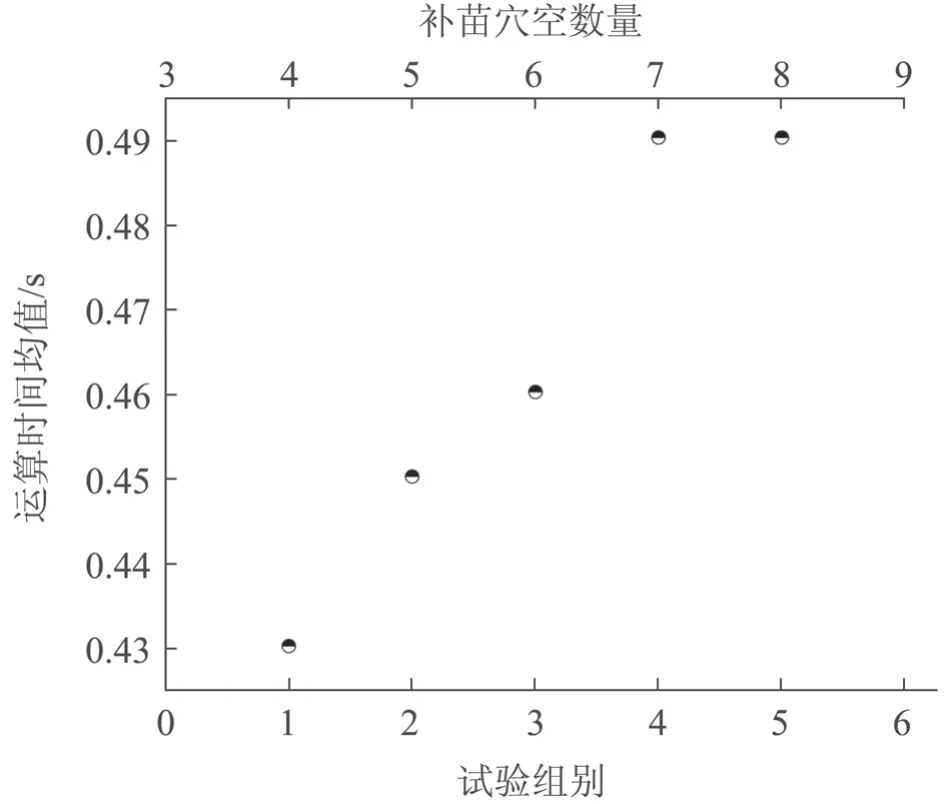
图10 多组试验下补苗穴孔数量与运算时间均值的关系
5 结语
1)构造的穴盘苗位置坐标和穴盘苗序号之间的映射关系公式为染色体的编码。补苗自动移栽遗传算法模型采取补苗穴盘与供苗穴盘序号交替布局的编码机制、最优个体保存与最差个体替换策略来避免算法陷入“局部早熟”。
2)针对规格为50 穴孔钵盘的补苗移栽仿真试验,补苗自动移栽遗传算法模型能快速获得最优的路径规划和最短的移栽路径长度,且对比标准遗传算法,获得的最优路径长度缩减了165 mm,缩减幅度为5.6%。
3)在规格为50 穴孔钵盘的补苗移栽仿真试验中,在补苗、取苗穴孔位置一定的情况下,补苗自动移栽遗传算法模型显示补苗穴孔数量与移栽路径长度均值、运算时间在趋势上均呈正比例关系。
