基于DTCWT的运动想象脑电特征提取
2023-05-08耿逸飞
汤 伟 耿逸飞
(陕西科技大学电气与控制工程学院 陕西 西安 710021) (陕西科技大学工业自动化研究所 陕西 西安 710021)
0 引 言
脑机接口(Brain-Computer Interface,BCI)是利用大脑所产生的信号来建立人脑与外部设备的信息控制的交互技术[1],在诸多方向有着显著的研究意义,如康复医疗[2]、游戏娱乐[3]等。运动想象是人对自身进行控制的意念活动。当人在想象单侧肢体运动时,对侧大脑皮层处于激活状态,相关的节律信号幅值会降低;而同侧处于阻滞状态,相关的节律信号幅值会升高。上述现象分别称为事件相关去同步(Event-Related Desynchronization,ERD)以及事件相关同步[4](Event-Related Synchronization,ERS)。因此,在ERS/ERD的基础上,我们能够实现对左右手运动想象任务的分类。由于大脑系统十分复杂,所产生的信号随机性强且不稳定,非线性特征显著,因此如何有效提取脑电特征成了一个难题。
目前,脑电信号常用的特征提取方法有:单一时域或频域方法、时频域结合方法和非线性分析方法等。其中前两种方法适用于分析平稳信号,应用于非平稳的脑电信号时效果不佳[4]。由于脑电信号具有显著的非线性特征,非线性分析方法十分适用于脑电信号,常用的方法有:香农熵、自回归(Auto Regressive,AR)模型参数、分形维数和Lempel-Ziv复杂度等[5]。孙会文等[6]提出的结合HHT与AR模型参数的脑电分类方法,分类识别率达81.08%,适应性良好。罗志增等[7]提出的基于多尺度Lempel-Ziv复杂度的特征提取方法,得到了较高的分类识别率,达87.87%。上述方法从非线性角度对脑电进行识别,都表现出了较高的识别率,但是特征选取考虑的都是单一角度,忽略了脑电信号在时频域所包含的有效信息[8]。因此本文提出一种时频域特征与非线性特征相融合的提取方法,从多个角度完备地描述脑电信号。
由于原始脑电中夹杂与运动想象无关的信号频段,本文引入双树复小波(Dual-tree Complex Wavelet Transform,DTCWT)对C3、C4通道的脑电信号进行最优频段选取,这样既去除了无关脑电频段,又进行频率分析,同时提高了分类准确率。在DTCWT分解基础上,选取Hilbert瞬时能量谱、边际能量谱和Lempel-Ziv复杂度作为脑电信号特征,最后采用线性判别分析对其实行分类。仿真实验表明,本文提出的基于DTCWT的多特征融合方法,相较于使用相同数据集的文献[9-10]方法,具有更大的最大互信息与更高的平均识别率。
1 实验数据与方法
1.1 实验数据
本文使用的数据为被测试者在进行左右手运动想象任务时采集的脑电信号,源自第三届国际脑-机接口(BCI Competition Ⅲ)的dataset Ⅲb。EEG信号按照国际10-20导联系统的C3、C4、Cz通道采集获得。该数据集包含3名受试者的实验结果,分别为O3VR、S4和X11。O3VR为400个试次,S4和X11皆为1 080个试次,每次实验时间为8 s,采样频率为125 Hz。单次实验过程如图1所示。

图1 单次实验过程
受试者安静坐在显示器前,根据屏幕提示进行左右手运动想象任务。0~2 s,屏幕空白,受试者进行放松;2~3 s,屏幕投放“+”,准备运动想象任务;3~9 s,屏幕显示左右方向箭头,受试者根据对应箭头进行运动想象任务。t=9 s时,实验结束。
1.2 实验原理
1.2.1 双树复小波变换
双树复小波不仅具有离散小波变换的多尺度分析的能力,同时有效解决了复小波变换中计算复杂的问题,相对于传统离散小波,可以较为精确地描述信号的细节信息,已成功应用于轴承故障分析和面部识别等领域[11]。
DTCWT采用实部树和虚部树对信号进行分解与重构,实部树和虚部树采用不同的实数滤波器组,从而得到实部系数与虚部系数,使得实部树与虚部树的信息互补,从而保证了信号分析的完备性。另外,DTCWT在多尺度分解中运用了二分法来降低冗余度,有效提高了算法的计算速度。
设脑电信号c(n)的采样频率为fs,用DTCWT将脑电信号分为L层,则能得到CAL、CDL、CDL-1、…、CD1等L+1子带的复系数。重构后得到的信号分量AL、DL、DL-1、…、D1所对应的频带范围分别为[0,fs/2L+1]、[fs/2L+1,fs/2L]、[fs/2L,fs/2L-1]、…、[fs/22,fs/2]。因此,DTCWT进行L层分解可得L+1个重构分量。
1.2.2 时频-非线性特征提取
在对脑电信号进行特征提取时,先进行DTCWT分解,得到一系列子频带,ERS/ERD现象主要发生在α(8~14 Hz)和β(14~30 Hz)节律,根据DTCWT的分解规则,分解尺度定为4层。子带和节律信号的关系如表1所示。

表1 子带信号和节律信号的对应关系
考虑到ERS/ERD现象,本实验只对D3与D2分量进行特征值求取,这样既能精确且完备地提取有效信息,又能降低特征向量维度。分别计算每个数据段的Hilbert瞬时能量谱(Instantaneous Energy Spectrum,IES)、边际能量谱(Marginal Energy Spectrum,MES)和Lempel-Ziv复杂度三个特征参数,从而构成时频域-非线性特征向量。对于单次实验数据,对C3和C4两个电极需要计算4个IES参数、4个MES参数、4个Lempel-Ziv复杂度参数,共计12个参数值组成12维特征向量。
3个特征参数的定义如下:
(1) 对于一个给定信号C(t),进行Hilbert变换[12]:
(1)
可得到解析信号:
Z(t)=C(t)+jY(t)=A(t)ejφ(t)
(2)
式中:A(t)和φ(t)分别为瞬时幅值和瞬时相位。
由A(t)和φ(t)求取瞬时频率ω(t):
(3)
则信号幅度在时-频域的分布情况,即Hilbert谱为:
(4)
式中:Re为取实部。
根据式(4)可求取IES和MES:
(5)
式中:[ω1,ω2]为频率范围;[t1,t2]为时间范围。
IES表现为时域能量特征,MES表现为频域能量特征。
(2) Lempel-Ziv复杂度描述了序列与随机序列的相似度,复杂度越大,序列新模式增加的速率越快,越接近随机序列[13]。设序列S(s1,s2,…,sn)的Lempel-Ziv复杂度为z(n),当n→∞时,z(n)会趋于定值n/logln,l为粗粒化段数(传统二值化时,l=2),则定义归一化Lempel-Ziv复杂度为:
(6)
为了验证上述三个特征能够较好地反映ERS/ERD现象,从流程的第1 s开始,采用滑动窗来提取特征,每次滑动1个采样点,直到最后1 s结束,从而获得单次实验任务的特征值时间序列。将同一运动想象任务的所有实验所得的特征值叠加平均,得到平均特征值时间序列。图2(a)为被试者O3VR左手运动想象的平均瞬时能量图,可以看出,在4~5 s的时间段内,被试者进行左手想象任务时,C3通道较C4通道具有更高的能量分布;图2(b)为被试者O3VR右手运动想象的平均瞬时能量图,进行右手想象任务时,C4通道较C3通道具有更高的能量分布,符合ERS/ERD原理。图3为左右手运动想象的平均边际谱幅值图,图3(a)为左手,图3(b)为右手。可以看出在8~15 Hz频段,两种不同动作的运动想象下,皆是C3通道具有较高能量,不符合ERS/ERD现象,但在15~30 Hz频段,信号的特征符合ERS/ERD现象。若从时域能量角度统一分析信号特征,低能高频信号所含有效信息会被高能低频信号覆盖,从而导致时域能量特征的敏感度下降、被试识别率差的结果。因此,本文利用DTCWT将信号拆分为成多个子频带分量,保证了有效信息的完整保留,提高了被试识别率。

(a)
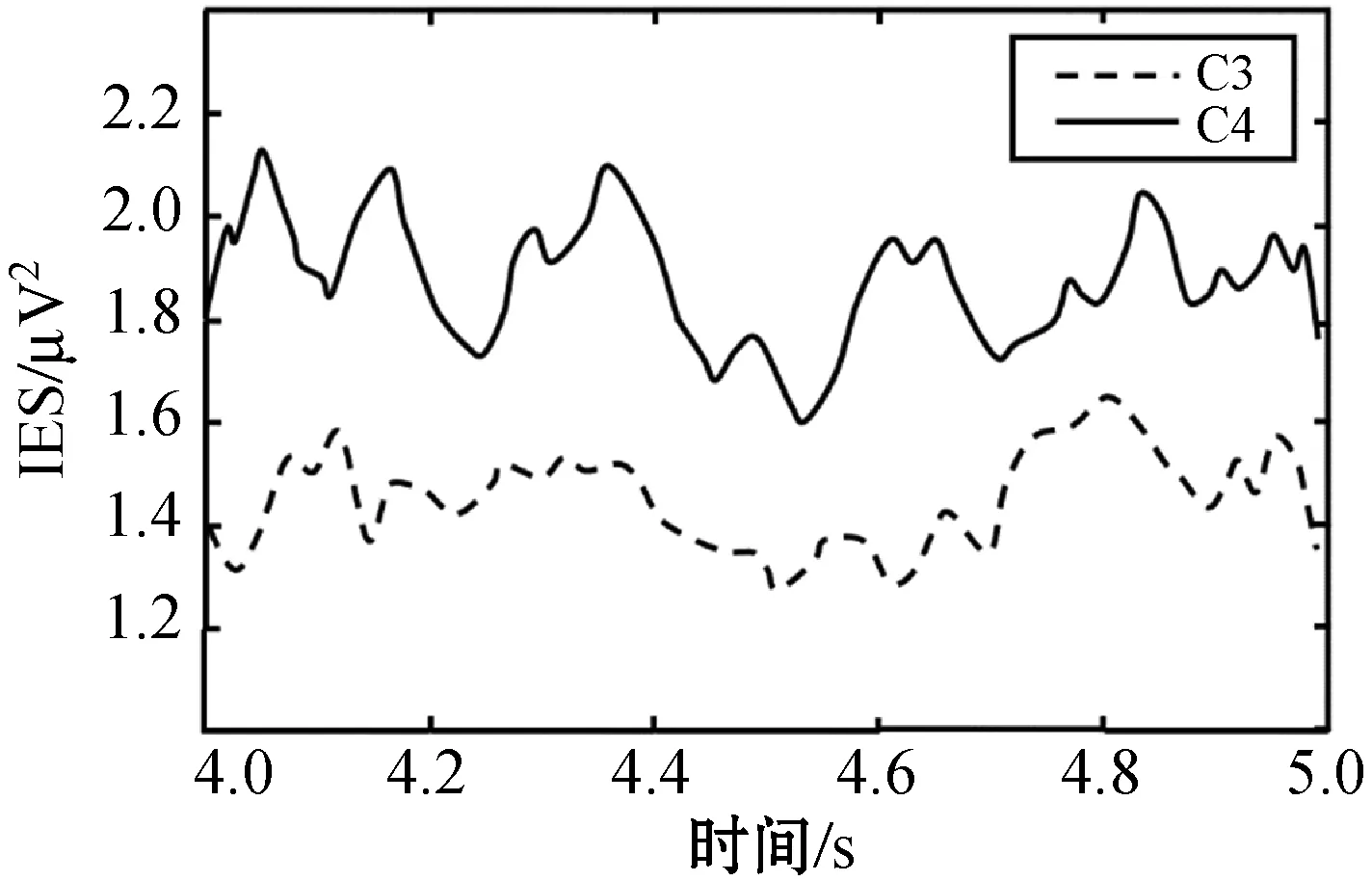
(b)图2 C3、C4的平均瞬时能量

(a)
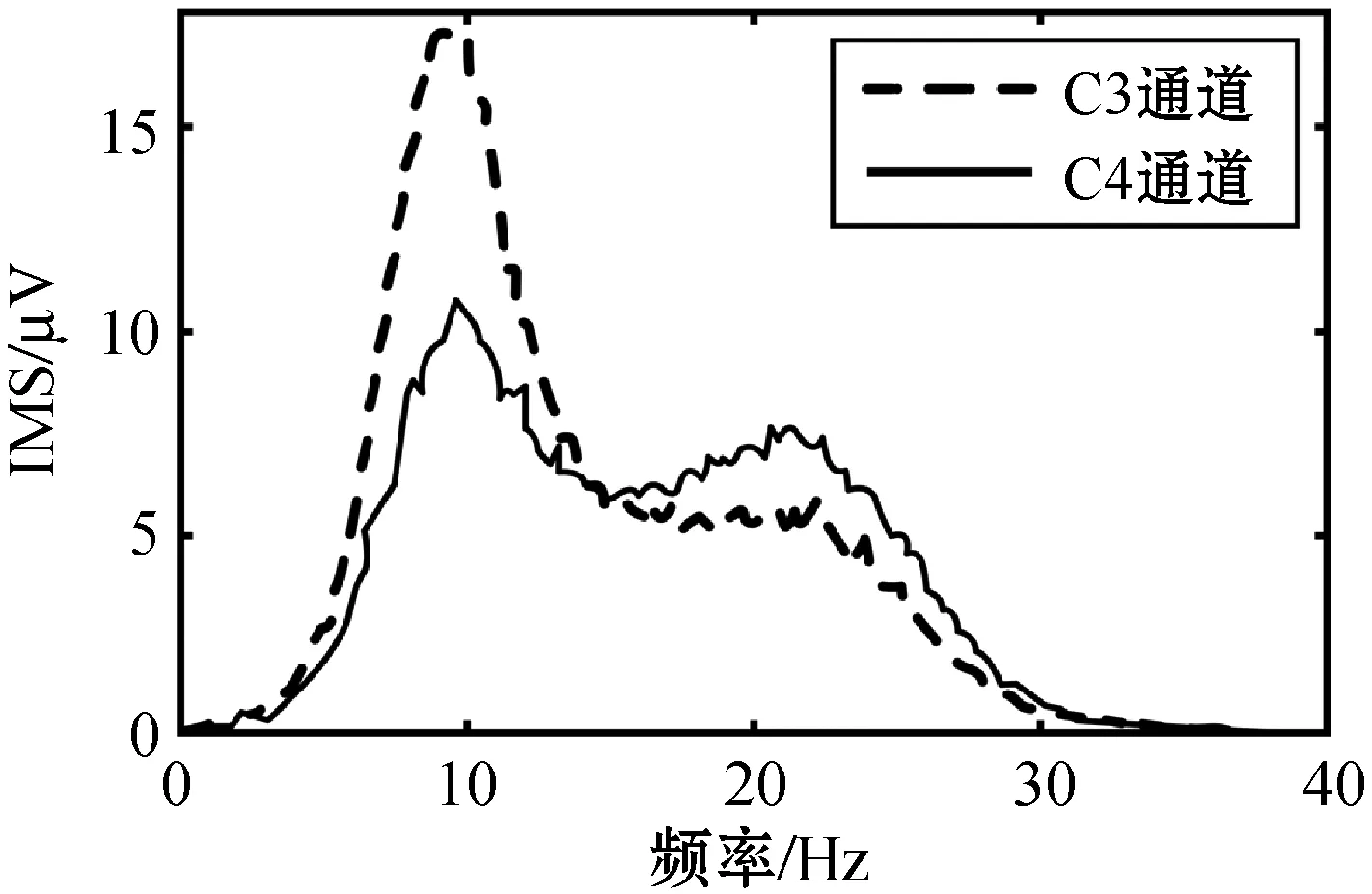
(b)图3 C3、C4的平均边际谱幅值
图4为左右手运动想象的平均Lempel-Ziv复杂度幅值图。图4(a)为想象左手运动,在3~5 s阶段,同侧C3电极复杂度减小,对侧C4电极复杂度增加;图4(b)为想象右手运动,亦出现了类似现象,故Lempel-Ziv复杂度符合ERS/ERD现象。
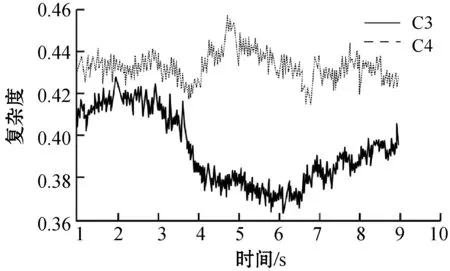
(a)

(b)图图4 C3、C4的平均Lempel-Ziv复杂度幅值
因此,综合上述分析,三种不同观测角度的特征都适合用来分析左右手想象运动。
脑电特征提取过程如图5所示。

图5 特征提取过程
1.2.3 分类方法及性能指标
线性判别分类器(Linear Discriminant Analysis,LDA)的基本思想是将训练样本投影后,使得类内方差最小,类间方差最大,即使同种类别数据的投影点尽量靠近,不同类别数据的类别中心间距离尽可能的大。
LDA实现步骤[14]如下:
(1) Fisher规则函数:
(7)
式中:向量Ω为投影方向;Sb是投影前两类别的类间;SΩ是类内离散度矩阵。
(2) 使用拉格朗日乘数法求解极值,约束条件为函数的分母为常数矩阵C:
L(Ω,λ)=ΩTSbΩ-λ(ΩTSΩΩ-C)
(8)
式中:λ为拉格朗日乘子。
(3) 将式(8)对Ω求偏导数,得到最佳投影方向:
(9)

本文引入分类准确率和互信息两个指标来评价本文方法的有效性[15]。
分类准确率定义如下:

(10)
互信息定义如下:
MI=0.5log2(RSN,t)+1
(11)
式中:RSN,t为信噪比。RSN,t表达式如下:
(12)

2 实验与结果分析
2.1 实验过程
实验环境为PC计算机:Windows 10 64位系统,8 GB内存,主频2.60 GHz。首先,依据运动想象所对应的大脑区域,选取C3和C4两个通道作为输入信号。对所选通道的脑电信号进行DTCWT变换得到不同频率范围的分量信号(见表1),根据ERS/ERD现象,D2与D3重构分量接近α和β节律,以便于精确地对EEG进行特征提取。
然后,对D2与D3分量计算瞬时能量谱IMS、边际能量谱MES和Lempel-Ziv复杂度三个特征参数,从而构成12维的时频域-非线性特征向量。
最后,采用分类器对脑电特征向量进行分类,LDA相较于支持向量机和神经网络,它不需要设置任何参数,不依赖隐含层节点的选择,在脑电识别方面具有良好的分类效果。因此选用LDA分类器来进行脑电想象运动的识别。本文采用4折交叉验证方式进行50次随机实验,将50次实验的平均识别率作为最终实验结果。由于实验时间的4~8 s为受试者的表现力最佳时期,因此选取该时间段进行实验验证。
2.2 多特征和单一特征的对比
为了方便,把瞬时能量谱IES记作特征F1,边际能量谱MES记作特征F2,Lempel-Ziv复杂度记作特征F3。受试者O3VR记作S1,受试者S4记作S2,受试者X11记作S3。采用不同特征进行分类,包括采用单一特征和采用多特征进行脑电分类,所得结果如表2所示。
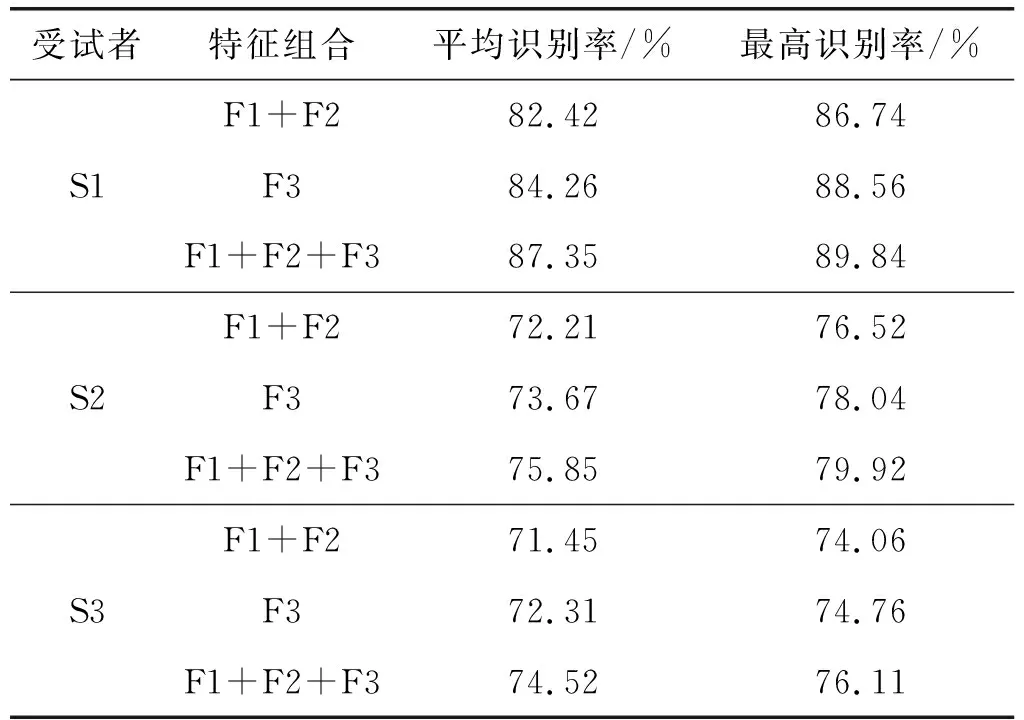
表2 不同被试者采用不同特征的脑电分类结果
可以看出,相同实验任务下,不同受试者的识别率不尽相同,是每个受试者对实验的敏感程度不同导致的。F1+F2为时频域特征,F3为非线性特征,同一受试者,采用时域特征进行运动想象分类的识别率没有采用非线性特征的识别率高,且三个受试者皆是如此,表明非线性特征能够更好地表征脑电信号中所蕴含的有效信息。本文提出的时频-非线性的组合特征(F1+F2+F3),相较于单一特征,识别率均得到了显著提升,这是由于组合特征对脑电信息进行了多角度的描述,完备地表征了脑电信号。表2实验数据表明,多种特征组合的分类效果明显优于单一特征。
2.3 多种识别方法结果比较
表3给出了本文方法与近期使用相同数据集的其他方法所取得的分类结果对比。文献[9]从非线性角度选取了相空间特征进行运动想象识别。文献[10]选用了小波特征并使用粒子群对分类器进行了优化。本文则是将时频域特征以及非线性特征结合组成时频域-非线性特征向量,从多个角度描述信号信息。由表3可知,本文方法的平均识别率均优于其他两种方法。

表3 不同方法所得到的最高识别率(%)
表4给出了不同方法下得到的最大互信息,其中包括BCI2003竞赛前三名获胜者以及文献[9-10]的实验结果。实验结果表明,本文方法相较于其他实验方法具有显著优势。

表4 不同方法的最大互信息
3 结 语
脑电信号是一种随机非线性信号,传统方法只采用单一特征或只考虑了时频域角度,而忽略了非线性这一特性,导致系统识别率较低。本文针对这一问题,提出一种基于DTCWT的运动想象脑电特征提取方法。首先,运用DTCWT近似平移不变性和有效的抗频谱混叠的特性,对脑电信号进行分解与重构,筛选得到与ERS/ERD现象更加匹配的信号分量。然后对筛选后的分量提取Hilbert瞬时能量谱IMS、边际能量谱MES和Lempel-Ziv复杂度三个特征,形成时频域-非线性特征向量。最后用LDA对特征进行分类识别。实验结果表明,引入非线性特征——Lempel-Ziv复杂度后,相对单一特征或时频域特征,识别率都得到了一定程度的提升,最高分类准确率为89.84%,平均识别率为82.12%,最大互信息值为0.88,表明了非线性分析结合时频域分析的优势。
