滑盖式节能日光温室结构静力分析及优化

刘艳华，王晓倩，王 聪，张 峰

（沈阳农业大学 水利学院，沈阳 110161）

节能日光温室是我国北方常用的温室类型，主要捕获和积聚白天的太阳能，并在夜间均匀释放热量[1-2]。日光温室不但使作物的生长季节得到了有效的延长[3]，而且解决了北方冬季蔬菜供应短缺的问题，也为农民增收提供了有效途径[4]。然而自然灾害对温室结构造成的破坏，使得经济损失极为严重。

滑盖式节能日光温室采用装配式结构，有效提高了日光温室的建造速度、土地利用率、蓄热保温能力等[5]，促进了我国日光温室现代化发展，获得良好的推广应用[6]。该温室骨架采用半弧形提高了稳定性，建造形式的改变也加强了抗风、雪的承载能力，解决了传统日光温室的缺点。但是其结构形式的改变，现仍缺乏对滑盖式节能日光温室结构力学性能的分析研究。

为提高温室的经济效益，国内外专家学者对日光温室的力学性能、结构稳定和结构优化进行了大量的研究[7-10]。王聪等[11]对雪荷载作用下几字型钢日光温室的钢截面进行优化分析；齐飞等[12-13]对不同跨度温室的杆件位置对温室结构稳定性的影响进行分析；丁敏等[14-18]通过ANSYS 有限元软件对不同荷载工况下的温室进行模拟，对传统日光温室的承载能力和结构进行分析与优化。目前对滑盖式节能日光温室主要侧重于温光性能方面的研究，TONG等[5-6]用辽沈Ⅲ型温室与滑盖式节能日光温室进行对照试验，对滑盖式节能日光温室温光性能进行研究。仅有王文武等[19]通过现场加载试验对滑盖式节能温室结构进行了力学分析，现依旧缺少对滑盖式节能日光温室整体稳定性，及骨架结构优化方面的研究。

本研究以滑盖式节能日光温室为研究对象，用ANSYS有限元分析软件模拟滑盖处于开、合状态时在风、雪荷载作用下结构的变形情况，分析滑盖式节能日光温室的力学性能，采用零阶优化的方法对温室骨架结构进行优化，以此得到最优解，从而达到提高经济效益的目的。

1 有限元模型及荷载组合

1.1 有限元模型

1.1.1 温室结构参数 本研究参考沈阳农业大学科研基地的滑盖式节能日光温室（图1），该温室采用半圆形的彩钢板滑动覆盖，温室总长60 m，跨度12 m，脊高4.6 m，屋面采光角41.5°，钢材选用Q235，前屋面选用0.1 mm厚的聚酯膜（PET）为透明覆盖材料。该温室屋面呈半圆结构，每榀骨架间隔2 m，共31榀骨架，依照农业温室结构设计标准[20]对骨架截面尺寸进行选取。每榀骨架之间由7根直径152 mm、壁厚3 mm的镀锌钢管作为横向系杆连接，单榀骨架屋顶处横向支撑与上弦杆选用直径140 mm、壁厚2.5 mm的镀锌钢管，屋顶处竖向支撑与下弦杆选用直径140 mm、壁厚3 mm的镀锌钢管，每间隔4榀桁架设直径140 mm、壁厚3.5 mm的镀锌钢管作为斜支撑，腹杆选用直径12 mm的螺纹钢筋。

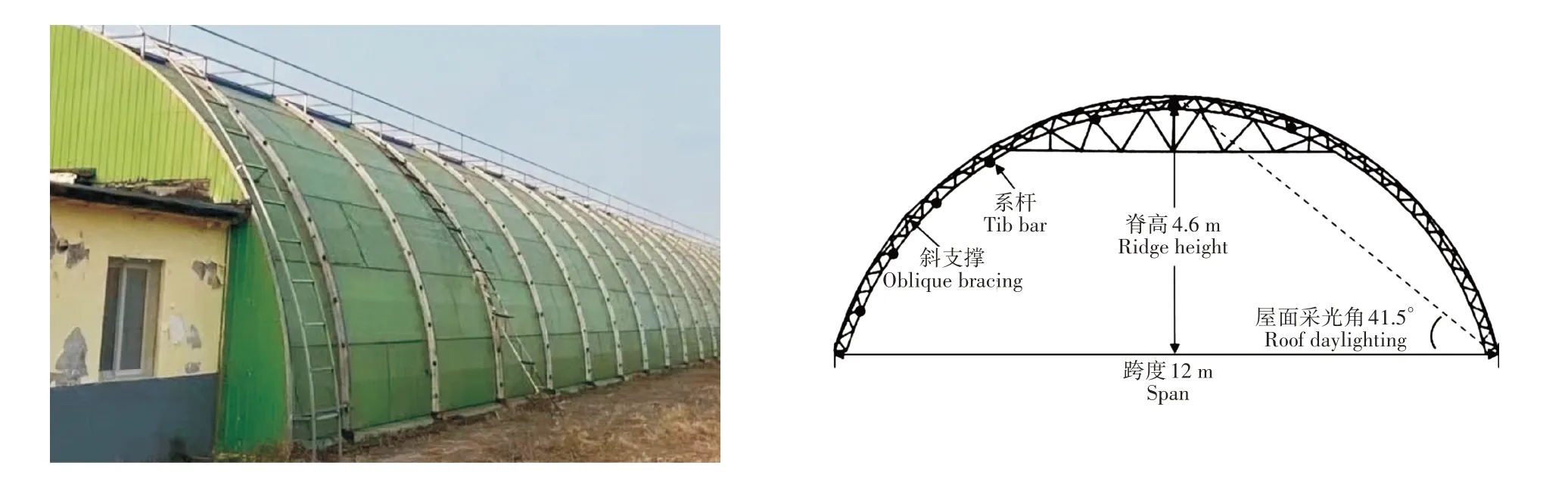
图1 滑盖式节能日光温室示意图Figure 1 Schematic diagrams of sliding cover solar greenhouse

1.1.2 单元类型的定义 有限元建模时，选取Beam188 和Shell181 单元来分别模拟滑盖式节能日光温室的骨架部分和滑盖部分。Beam188单元适用于分析细长和中等粗短的梁结构，该单元基于Timoshenko梁理论，考虑了剪切变形的影响，也适合线性、非线性以及大角度转动大应变问题。Shell181是一个4节点单元，每个节点有6个自由度（X、Y和Z方向的平移，以及围绕X、Y和Z轴的旋转）是一种适用于分析薄到中等厚的壳结构。

1.1.3 有限元模型的建立 建模过程中，因Beam188单元与Shell181单元自由度各不相同，为保证力和弯矩的正常传递，本研究采用耦合自由度的方法对滑盖式节能日光温室的桁架与滑盖两个不同单元之间各节点进行连接。日光温室骨架由焊接连接组成，桁架通过预埋件固定在基础上，建模过程中将其底部节点视为刚接。为了考虑整体空间效应，其有限元模型建立的滑盖式节能日光温室5榀桁架模型图如图2。

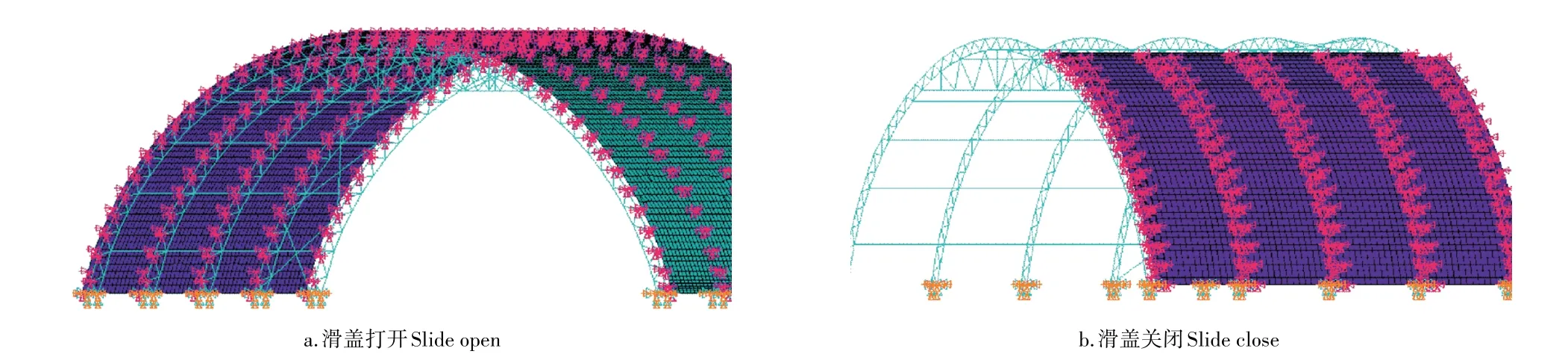
图2 滑盖式节能日光温室5榀桁架模型图Figure 2 Sliding cover solar greenhouse model drawing of 5 trusses

1.2 荷载计算和组合方法

日光温室荷载主要包括永久荷载和可变荷载，其中永久荷载为结构自重和安装在结构构件或围护构件上的固定设备自重等，可变荷载包括作物荷载、风荷载、雪荷载、屋面活荷载、安装在结构构件上的移动设备荷载、温度作用和地震作用等[21]。

1.2.1 永久荷载 滑盖式节能日光温室的覆盖材料选取0.15 mm 的聚乙烯膜（PE），因其自重产生的荷载小于1.5 N·m-2，故忽略不计。依据温室结构荷载规范[21]，温室内固定设备荷载尚未确定时，竖向均布荷载按700 N·m-2计算。

1.2.2 可变荷载

（1）风荷载。结合温室结构荷载规范，可知风荷载的计算公式为：

式中：ωk为风荷载标准值（kN·m-2）；μs为风荷载体型系数；μz为风压高度变化系数；ω0为基本风压（kN·m-2）；风荷载体型系数与屋面形状有直接关系。滑盖式节能日光温室的风荷载体形系数按图3 数值计算。温室所在地属B 类地区，温室离地高度4.6 m，则风压高度变化系数取值为μz=0.79。基本风压应按照规范取值为ω0=0.55 kN·m-2。

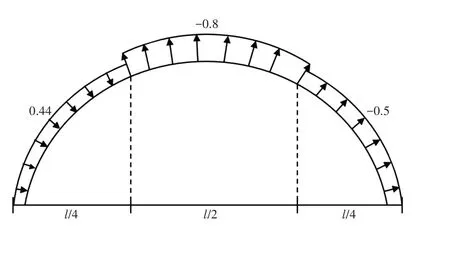
图3 滑盖式节能日光温室风荷载体形系数Figure 3 Wind load type coefficients of sliding cover solar greenhouse

（2）雪荷载。雪荷载标准值按荷载规范计算：

式中：sk为雪荷载标准值（kN·m-2）；μr为屋面积雪与分布系数；ct为加热影响系数；s0为基本雪压（kN·m-2）；屋面积雪分布系数与屋面形状有关，其雪荷载体型系数见图4。飘雪影响造成的非均匀雪荷载取值μr,m=2.0、均匀分布雪载取值μr=0.4。温室覆盖材料为单层塑料膜，不加温温室，按规范选取加热影响系数ct=1.0，基本雪压s0=0.38 kN·m-2。

图4 滑盖式节能日光温室雪荷载体形系数Figure 4 Distribution coefficients of snow load for the greenhouse

（3）作物荷载。作物荷载应包括吊挂在温室结构上的作物、栽培容器及容器内基质等的重量。由图5 可知，所种植物为番茄，该温室种植茄果类、西甜瓜类作物的单位面积荷载Ck=0.15 kN·m-2。

图5 温室作物Figure 5 Greenhouse crops

（4）施工活荷载。屋面构件计算时，施工检修集中荷载标准值可1.0 kN，且作用在结构最不利位置上[21]。日光温室中的屋面活荷载主要是操作前屋面保温被的操作人员的重量，因此按照规范取人工荷载Lk=1.0 kN。

1.2.3 荷载组合方法 结合GBT51183-2016，荷载基本组合的效应设计值Sd计算公式为：

式中：γG为永久荷载分项系数（kN·m-2）；γQi为第i个可变荷载分项系数，其中γQ1为主导可变荷载的分项系数；SGk为永久荷载标准计算值的荷载效应值（kN·m-2）；SQik为按第i个可变荷载标准值计算的荷载效应值（kN·m-2）；ψci为第i个可变荷载的组合系数；n为参与组合的可变荷载。荷载组合分析时，为探究每一种荷载类型对结构变形的敏感情况，选取4 种荷载工况。工况1、工况2和工况3分别为反考虑均布雪载作用、非均布雪载作用和风载作用对滑盖关闭状态下节能日光温室结构变形的影响。工况4 是仅施加风荷载对滑盖打开状态下节能日光温室结构变形的影响。4 种荷载工况中屋顶的作物荷载、雪荷载和施工荷载的系数均为1.2，而永久荷载和风荷载的系数为1.0，对于参与荷载组合的可变荷载组合的荷载组合系数均取0.7，而对于不参与荷载组合的永久荷载和主要可变荷载（风、雪荷载）的组合系数取1.0[16]。其荷载工况汇总如表1。

表1 荷载组合系数及分项系数Table 1 Load combination coefficient and component coefficient

2 结果与分析

2.1 有限元模型的验证

滑盖式节能日光温室较传统日光温室建模而言，主要区别就是需完成Shell181 与Beam188 单元的耦合。传统日光温室其结构在有限元分析过程中，荷载直接作用在梁单元上，且传统日光温室在结构分析的有限元建模仅由Beam188单元完成温室模型的建立。因此，本研究的模型验证，主要是对壳梁单元耦合模型施加荷载的验证。

结合王文武等[19]对滑盖式节能日光温室钢桁架进行对称加砖模拟均布荷载的现场试验，通过非电量电测技术得到桁架的应力应变值。本研究选用ANSYS有限元分析软件，对本研究的滑盖式节能日光温室进行有限元模型的验证。以焊接点作为关键点创建温室模型；为考虑整体空间效应，共建立3 榀桁架进行模拟，并对其底端进行固定，施加相应大小的荷载；滑盖与桁架之间通过耦合自由度的方法完成Beam188和Shell181不同单元之间的连接。对中ab段杆件进行静力学分析，将ab段杆件的模拟值与试验值进行比较验证（图6）。

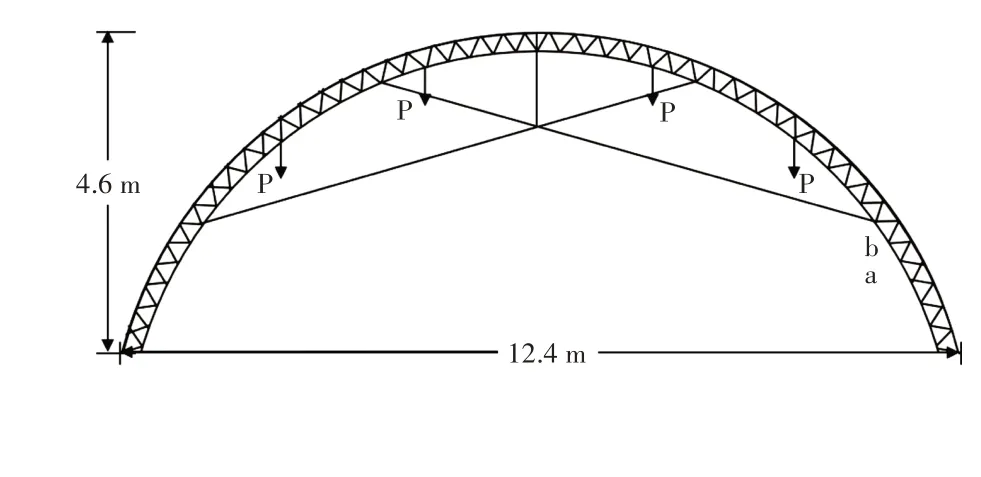
图6 试验模型单榀桁架简图Figure 6 Schematic diagram of a single truss for the test model

由图7可知，因现场试验过程中，仅对一榀桁架进行加载试验，未考虑相邻桁架的作用；且在进行现场试验之前，该试验温室已经使用运行两年时间，在使用过程中发生了一定变形，所以现场测试试验结果是在结构已经变形基础上，加砖模拟荷载的变形结果。而采用有限元模拟过程中，既考虑了相邻桁架间的作用，又考虑了在施加荷载是温室桁架处于未变形状态下，因此造成模拟与试验结果产生了误差。模拟结果与测试结果之间最大的相对误差在6%以内，其误差均小于10%，证明该有限元模型可以使用。

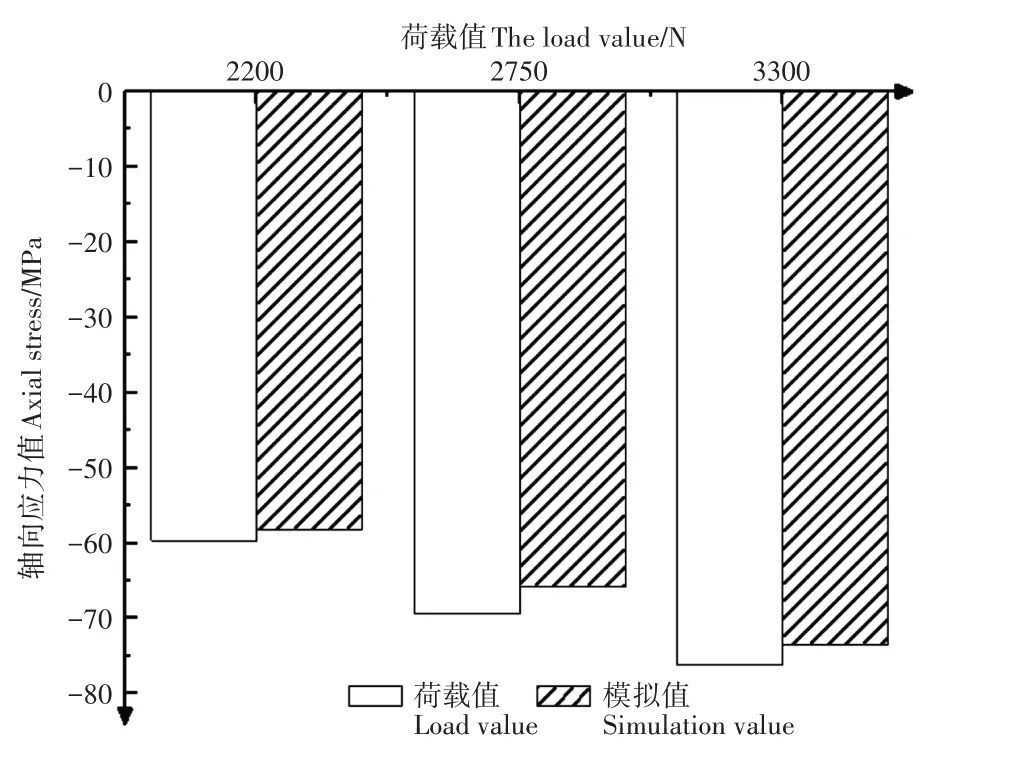
图7 应力值比较Figure 7 Comparison of stress values

2.1.1 静力学分析 本研究对4 种荷载工况下的温室模型进行应力和变形分析，以确定出最不利荷载组合，并对结构在最不利荷载组合下进行稳定性分析和结构优化。

（1）应力分析。滑盖式节能日光温室通过等效应力Von Mises stress 来描述其应力状态，不同荷载工况下的应力分析如表2。其中滑盖关闭状态下3 种不同工况下各杆件的等效应力布曲线如图8，不同荷载工况下的最大等效应力均出现在北墙固定端位置。温室两端刚接固定于混凝土，因此两端应力较大。前屋面角大于60°时，依据规范[21]，无雪荷载作用，所以工况1和工况2在屋顶部分的变化有较为明显的上升趋势，且温室顶部位置设有支撑杆件，增强结构稳定性。工况3 因风对温室顶部和北墙部分产生方向相反的吸力，屋顶及北墙处工况3 作用下产生的应力最小，前屋面处应力值均大于其他位置，前屋面工况1 作用下的上弦杆件等效应力为131 MPa、工况3 作用下前屋面上弦杆件的等效应力为95.9 MPa、其上弦杆最大等效应力为工况2作用下前屋面的应力值142 MPa。（2）变形分析。根据《农业温室结构设计标准》[20]，大跨度钢结构的位移变形应低于温室跨度的1/250，滑盖式节能日光温室即48 mm（12000/250），不同工况发生的位移变形如表3，皆满足位移设计要求。滑盖关闭状态下，风、雪荷载作用后，其最大位移均发生在同一位置，即第4 榀和第5 榀骨架之间的第3 个斜支撑上。由表3可知，滑盖关闭状态下施加非均匀雪荷载后的总位移值最大值为2.07 mm＜48 mm。滑盖打开状态下，因前屋面直接受到风荷载的作用，所以其位移变形也主要发生在前屋面，导致横向和纵向位移较大，且最大总位移发生在肩部位置的斜支撑上，其值为4.03 mm＜48 mm，同样满足位移设置的要求。

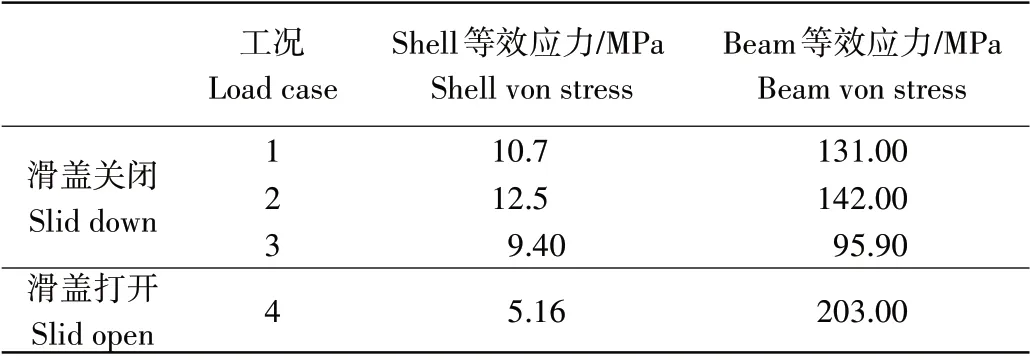
表2 荷载工况下实体单元应力最大值Table 2 Stress of solid element under different load conditions

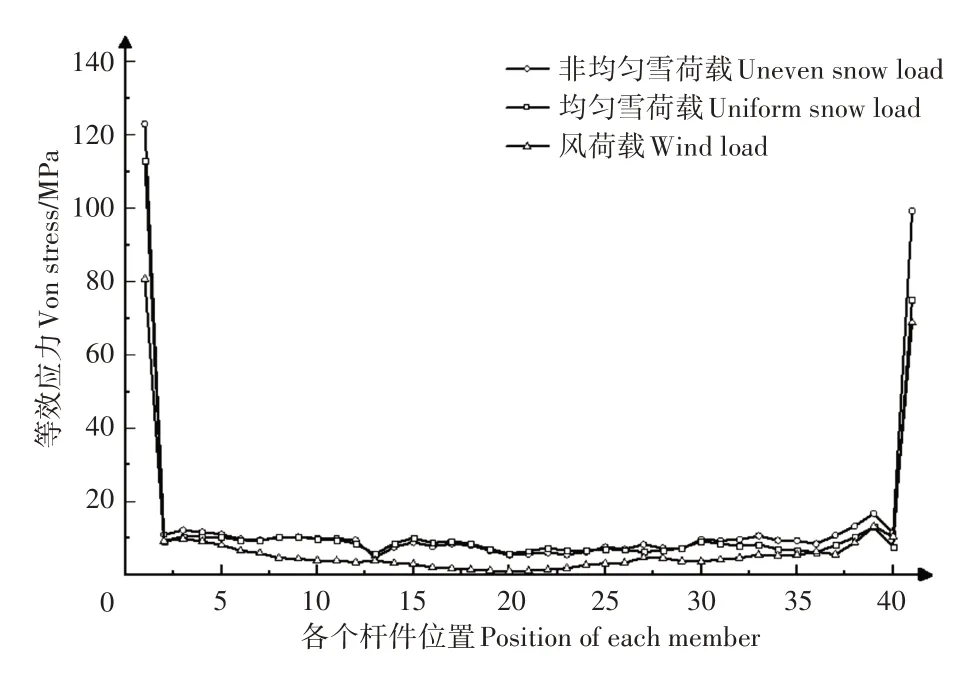
图8 滑盖关闭时各工况下杆件的等效应力分布曲线Figure 8 Equivalent stress distribution curve

由表2和表3可得到，4种荷载组合工况下的最大位移为4.04 mm，最大等效应力为203 MPa，综上可知最不利荷载组合为滑盖打开状态时施加风荷载（即荷载组合工况4）。

表3 荷载工况下实体单元位移最大值Table 3 Displacement of solid element under different load conditions

2.1.2 结构稳定性分析 滑盖式日光温室的结构稳定性分析，主要进行特征值屈曲分析，研究杆件的屈曲破坏。屈曲特征值可正可负，在ANSYS 有限元分析软件中有LANB 和SUBSP 两种计算方法。本研究采用LANB进行6次迭代，对滑盖关闭状态下最不利荷载和滑盖打开状态下进行的屈曲分析，其各阶模态系数如表4。表4中的数据均大于1，说明所施加的荷载均未超过屈曲荷载限值，该结构整体稳定性满足结构安全要求。

表4 滑盖不同位置下特征值屈曲模态系数Table 4 Eigenvalue buckling modal coefficients at different positions of slide cover

2.2 结构优化分析

结构优化是结构安全性和经济性的统一，常见的优化形式主要分为两种形式：一种是用有限元迭代优化，获取复合材料应力比和稳定性的构件最小截面尺寸；另一种则是对构件或结构的形状进行优化。采用ANSYS有限元分析软件中零阶优化的方法对滑盖式节能日光温室进行结构优化，获取杆件所在最优位置[16]。优化前先是通过特征值屈曲分析的方法对滑盖式节能日光温室的稳定性进行分析，并根据得出的稳定性控制系数进行变化范围的选取与确定。

2.2.1 目标函数的建立 将温室质量最小作为目标函数，桁架的总用钢量为：

式中：m为桁架总用钢量；ρ为桁架的刚材密度；Ai为第i根杆件的截面面积；li为第i根杆件的长度。

则目标函数f(x)计算公式为：

以最大位移、等效应力和特征值屈曲系数作为状态变量，把桁架的横截面积和滑盖的厚度作为设计变量，进行有限元模型的稳定性分析。滑盖式节能日光温室优化设计的一般数学模型为：

式中：D1为滑盖厚度；D2为上弦杆截面外圆半径；D3为下弦杆截面外圆半径；D4为斜支撑截面外圆半径；D5为钢筋的截面尺寸；D6为系杆截面外圆半径；Smax为等效应力；Umax为最大位移；Freq1为稳定控制系数。滑盖式节能日光温室桁架选用的是Q235 的钢，钢材密度为7850 kg·m-3。文中将总用钢量质量最轻作为目标函数进行结构优化。

2.2.2 优化过程 ANSYS有限元软件的优化步骤主要是：（1）用*CREAT命令完成分析文件的生成；（2）用/OPT命令进入优化模块对分析文件进行指定；（3）根据上述范围对设计变量、状态变量和目标函数进行指定；（4）选用零阶优化作为优化方法；（5）设置优化迭代次数，本研究设置允许迭代50 次，收敛精度为0.01 的非可行域内迭代20 次；（6）选用OPLIST 命令对优化迭代列表。优化计算可知，共迭代29 次后优化迭代完成，最优解为第24次迭代结果，优化前后各参数如表5。

由表5可知，优化后的目标函数减小，其等效应力和最大位移较优化前均有所提高，骨架利用更加充分，优化后的总用钢量较优化前降低1.63%，优化结果不显著。优化前后最大等效应力所在位置均在北墙固定端，其最大位移位置由屋顶处第10根系杆变为前屋面部分的第3根系杆处，提高了温室稳定性。因滑盖式节能日光温室桁架间隔以及位置选取，已是结合我国对传统日光温室结构优化基础上进行。但滑盖式节能日光温室不同于传统温室的建造形式，仅有王文武等[11]通过现场加载试验，对温室结构的研究。本研究通过有限元分析软件，用耦合的方法使滑盖与桁架之间完成力学传递，并对温室整体稳定性进行分析，对骨架截面尺寸进行优化。

表5 优化前后参数对照Table 5 Comparison of parameters before and after optimization

2.2.3 优化结果分析 目标函数的迭代曲线图如图9，梁单元截面的迭代曲线如图10。由图9 和图10 可知，所以参数均在25次迭代后趋于收敛，系杆是起到提高各榀桁架间稳定性的作用，因此上、下弦在优化过程中其杆件逐渐减小，系杆截面尺寸也随之改变。结构在符合安全范围的前提下，通过更充分地利用杆件使结构得到优化。

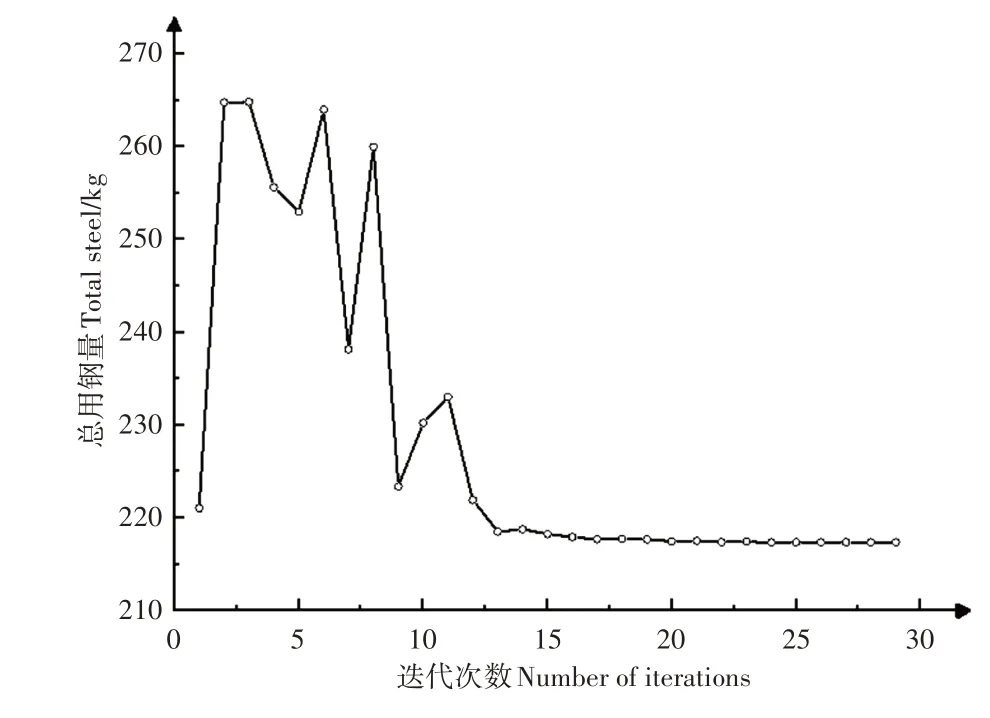
图9 目标函数迭代曲线Figure 9 Objective function iteration curve

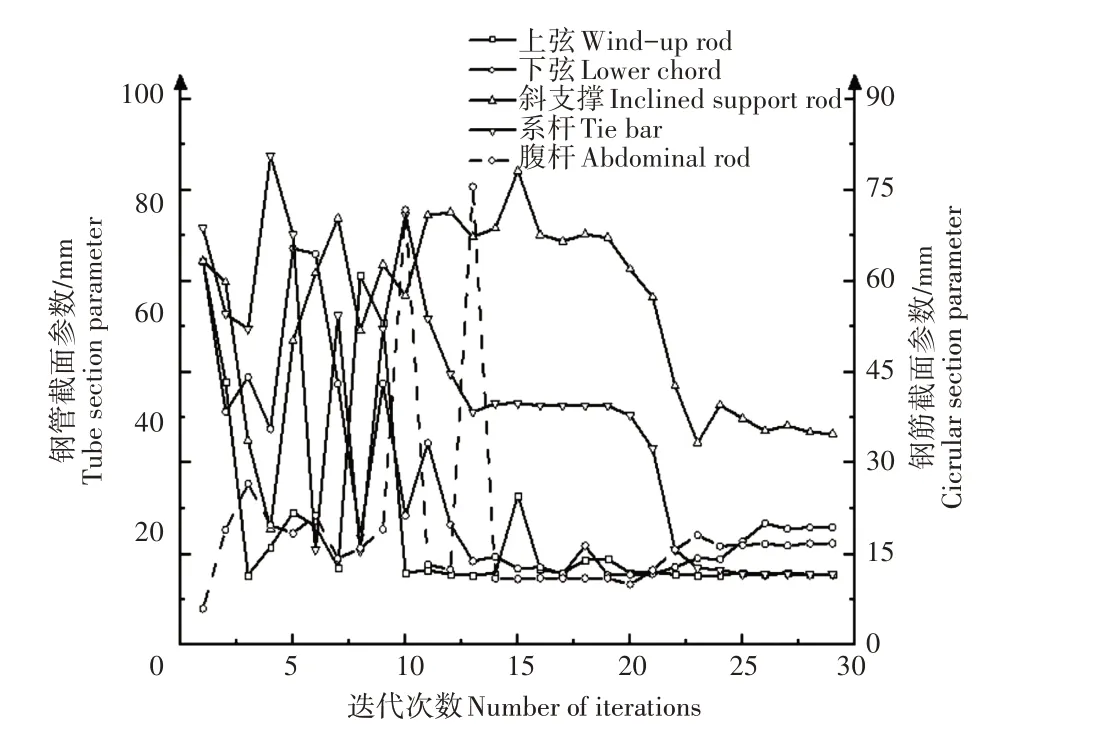
图10 梁单元截面尺寸迭代曲线Figure 10 Beam element section size iteration curve

现对优化后的各截面应力、最大位移等参数进行分析，其分析结果如表6。优化后的最大位移7.87 mm＜48 mm(12000/250)，优化后实体等效应力228 MPa＜235 MPa，其位移、轴向应力值均满足结构设计要求。

表6 优化后结果分析Table 6 Analysis table of optimized results

综上可知，滑盖式节能日光温室优化后其等效应力增加42.6%，杆件较优化前得到了更加充分的利用，且优化后总用钢量减少，达到了减低材耗提高经济效益的目的。

2.2.4 结构参数影响 分析优化后各个杆件的截面尺寸，发现上弦杆的变化最大。通过对上弦杆截面尺寸与应力进行分析，获得上弦杆长细比与等效应力变化曲线如图11。由此可得上弦杆长细比与等效应力表达式为y=8.9x+175.5，长细比越大等效应力越大。

图11 上弦杆长细比与等效应力迭代变化曲线Figure 11 Iterative curve of upper chord slenderness ratio and equivalent stress

温室下弦杆件与等效应力关系曲线如图12。由图12 可知，下弦杆长细比与等效应力的关系表达式为y=5.1x+205.7。

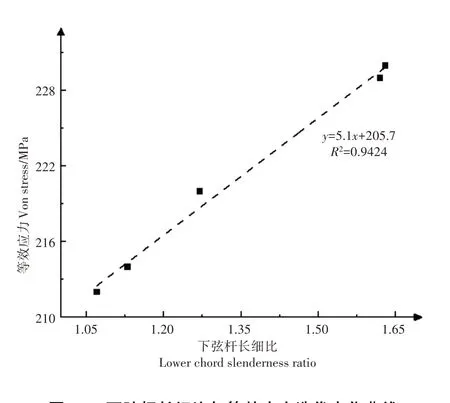
图12 下弦杆长细比与等效应力迭代变化曲线Figure 12 Iteration curve of slenderness ratio and equivalent stress of lower chord

3 讨论与结论

本研究对滑盖式节能日光温室进行力学分析及结构优化，优化后用钢量降低，有效提高了经济效益。力学分析结果表明，该温室结构对非均匀雪载更为敏感，该结果同REN 等[7]对20 m 塑料温室分析所得结果一致。滑盖在开、合两种状态下施加非均匀雪荷载的整体结构稳定性均符合结构安全要求。优化分析结果表明，可以根据所得关系式对温室骨架进行优化，从而降低温室的建造成本。但本研究仅考虑了静态荷载的施加与分析，今后可以考虑风荷载的震动、动力响应等动态荷载对滑盖式节能日光温室的作用，对滑盖式节能日光温室的力学分析更加完善。

本研究采用有限元模拟的方法，考虑滑盖在开合状态下，各荷载组合工况对温室结构的影响，探讨最不利荷载组合工况下的滑盖式节能日光温室整体稳定性和结构优化分析，结果表明，滑盖打开状态时风荷载作用下所得等效应力与位移最大，值分别为203 MPa和4.04 mm。对滑盖打开状态时施加风荷载作用进行结构优化分析，优化迭代28次得到最优解，优化后的钢材用量降低1.63%。优化后上弦杆截面尺寸变化最大，优化前后百分比为81.84%。分析上弦杆的截面参数与等效应力的关系，得出两者关系曲线为y=8.9x+175.5。分析下弦杆截面参数与等效应力的关系，可得两者的关系式为y=5.1x+205.7。