复杂道路智能汽车运动综合控制策略

2023-05-08秦国庆赵环宇江子旺

昆明理工大学学报(自然科学版) 2023年2期

冯樱,秦国庆,赵环宇,江子旺

(湖北汽车工业学院湖北省汽车动力传动与电子控制重点实验室,湖北十堰 442002)

0 引言

智能汽车是一个集环感、决策和运动控制于一体的综合系统,其中运动控制是实现智能驾驶的关键.随着研究的深入,人们希望车辆能够稳定、精确地跟踪期望路径的同时,还具备专业赛车手的驾驶技能,完成漂移过弯等极限运动.

目前,智能汽车路径跟踪控制方法主要有比例积分微分(Proportional-Integral-Differentive,PID)控制、模糊控制、LQR控制和MPC控制等.赵熙俊等[1]提出一种基于车辆道路动力学模型的鲁棒PID控制器,调整不同车速区间的PID参数,实现了车辆的路径跟踪.Silva等[2]以航向角误差和横向位移误差为控制输入,前轮转角为输出设计模糊控制器,获得较好的跟踪效果.胡杰等[3]设计出一种模糊LQR控制策略,车辆在不同车速下都具有较高的跟踪精度,却无法处理约束问题.MPC具有预测模型、滚动优化和反馈矫正的特点,可处理系统多约束问题,常用于路径跟踪控制器的设计[4].针对复杂道路环境,参考文献[5-6]设计了一种考虑系统多约束的MPC控制器,能在U形弯道和双移线工况下保持良好的跟踪效果和稳定性,改善了车辆对速度和路况的适应能力.在路径跟踪控制的基础上,考虑车辆避障功能,王翔昌等[7]提出一种改进人工势场算法,引入椭圆势场以调节障碍势场作用,在不同的障碍场景下具有较好的避障效果,却容易陷入局部最优问题.裴以建等[8]在快速扩展随机树(Rapidly-Exploring Random Tree,RRT)算法的基础上提出一种新的路径规划算法,采用人工势场法优化采样过程,提高计算效率.刘洋[9]基于MPC原理设计了一种带有重规划层的路径跟踪控制器,通过跟踪局部路径实现避障.

上述运动控制都处于车辆稳定域内,随着汽车控制技术的发展,学者开始关注车辆极限运动控制的研究[10].漂移是一种典型的极限运动,王鹏和Park等[11-12]根据参考路径和参考质心侧偏角,求解漂移平衡点并设计LQR漂移控制器,通过前馈加反馈的方式实现车辆的稳态漂移.在此基础上,Goh等[13]将参考轨迹视为一系列不稳定漂移平衡点,设计出一种能够在漂移平衡点处跟踪参考路径的漂移控制器.此外,纪奕沛[14]考虑漂移平衡点的切换,建立深度确定性策略梯度网络,分析训练损失值和最终训练回合的状态量,实现“8”字漂移.

车辆运动控制相关的研究主要针对路径跟踪或极限漂移运动作单独考虑,本文设计出一种集路径跟踪、避障和漂移于一体的车辆综合控制器.正常驾驶环境下,车辆路径跟踪行驶;若障碍物处于控制器预测范围内时,跟踪局部避障路径进行避障;过弯时,可在指定区域漂移过弯.设计复杂道路场景,并基于Matlab软件进行仿真实验,验证该控制器的有效性.

1 车辆模型

车辆操纵稳定性研究中,一般采用经典的二自由度车辆模型,仅考虑横向和横摆运动,而漂移过程中,需要调节车轮驱动力或制动力大小来维持漂移状态.因此,在二自由度模型的基础上,考虑车辆纵向作用力,建立后轮驱动的三自由度车辆动力学模型[15],如图1所示.

图1 三自由度车辆动力学模型Fig.1 Three degree of freedom vehicle dynamics model

图中,xoy为车辆坐标系;Ux、Uy分别为车辆质心纵向、侧向速度;αf、αr分别为前、后轮胎侧偏角;φ为横摆角.由车辆横向、纵向力平衡和横摆力矩平衡得到车辆动力学方程:

式中:m为整车质量,kg;a、b分别为质心o至前、后轴的距离,m;ax、ay分别为车辆质心纵向、侧向加速度;Fyf、Fyr分别为前、后轮侧向力;Fxr为后轮驱动力;δf为前轮转角;r为横摆角速度;Iz为车辆绕z轴的转动惯量.

同时,对质心侧偏角β做近似处理:

整理式(1)和(2),可简化得到:

式(3)中的轮胎侧向力由改进的Fiala轮胎模型得到:

式中:Cαi为轮胎侧偏刚度;αi为轮胎侧偏角;Fzi为轮胎垂直载荷;γi为衰减因子;αsl为侧偏角临界值;μ为路面附着系数;f和r分别表示前轮和后轮.

由于车辆是后轮驱动,前轮没有施加纵向力,前轮衰减因子γf为1;而后轮衰减因子γr随后轮驱动力变化而变化:

2 控制系统设计

为适应复杂的行驶环境,设计路径跟踪、避障和漂移控制器,实现车辆运动综合控制.

2.1 路径跟踪控制器

路径跟踪过程进行横、纵向单独控制:采用MPC控制算法设计横向控制器,采用比例积分(Proportional-Integral,PI)控制器调节纵向车速.车辆行驶过程中,实际路径用大地坐标系表示,车身坐标系和大地坐标系间的转换关系为:

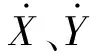
综合式(3)和式(7)～(8),得到非线性车辆系统:

式中:状态量χ=[Uy,Ux,φ,r,Y,X]Τ;控制量u=δf;X、Y为车辆在大地坐标系中横、纵向位置.

对式(9)进行离散化和线性化处理,得到线性方程:

χ(k+1)=Ak,0χ(k)+Bk,0u(k)-d(k)

(10)

d(k)=χ0(k+1)-Ak,0χ0(k)-Bk,0u0

(11)

为了对控制增量进行约束,定义新的状态量:

Δu(k|t)=u(k|t)-u(k-1|t)

(13)

新的状态空间表达式为:

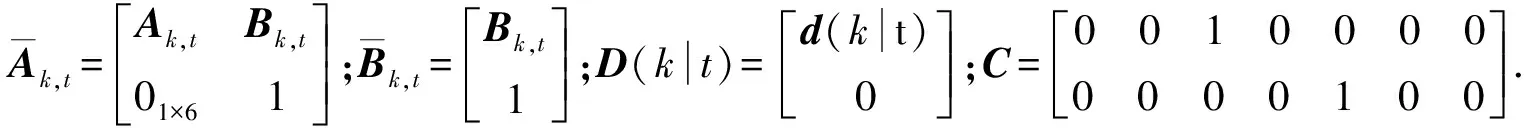
最终,预测时域Np输出方程为:

Yc(t)=ψtξ(t|t)+ΘtΔUc+ΓtΦt

(15)

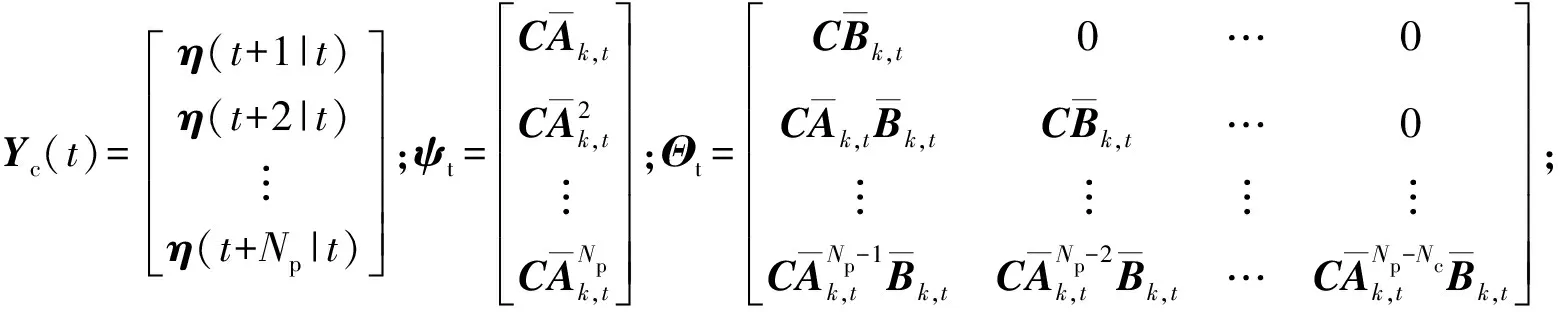
为了保证路径跟踪的精确性、稳定性,定义路径跟踪目标函数:

式中:ηref=[φref,Yref]T为输出量参考值;Np和Nc分别为预测时域和控制时域,ρ为权重系数,ε为松弛因子以防止无解,Q1和R1分别为输出量偏差权重矩阵和控制增量权重矩阵.

为方便求解,定义E=ψtξ(t|t)+ΓtΦt-Ycref,将式(16)转化为标准二次型求解问题:

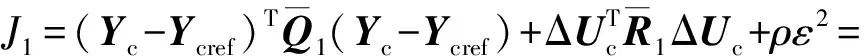
(17)

经过目标函数求解,得到当前时刻控制时域内控制增量序列,取首个解计算得到实际控制量,不断地滚动优化直至结束.为调节车辆行驶过程的纵向车速,采用PI控制器进行纵向控制,后轮驱动力为:

(18)

式中:kP、kI为比例系数;eUx为纵向车速误差.

2.2 避障控制器

为了确保车辆行驶安全性,且易于处理避障路径的运动学约束,采用MPC算法设计避障控制器.选择复杂度较低的点质量模型:

式(19)可以用下面非线性系统表示:

图2 障碍物模型Fig.2 Obstacle model

避障控制算法的推导过程与路径跟踪控制算法类似,在此不再赘述.障碍物信息以障碍物点的形式给出,并对尺寸较大的障碍物进行分割处理,如图2所示.(Xobs,i,Yobs,i)为障碍物点坐标(i=1,2,…,N).

避障路径规划算法的设计原则为:1)在能够安全躲避障碍物的前提下,尽量接近参考路径;2)规划出的局部避障路径要满足车辆运动学约束,以提高跟踪精度.定义避障目标函数:

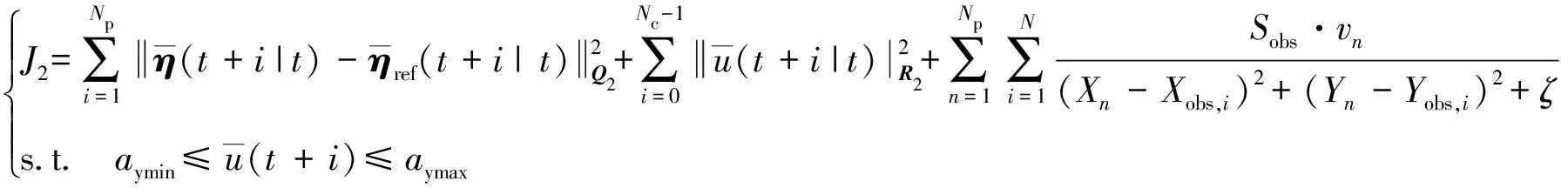
(21)

局部避障路径以离散点的形式给出,规划层和控制层步长不一致时,会降低跟踪精度.因此,采用5次多项式对离散路径点作拟合处理,且拟合曲线一、二阶连续,符合车辆运动学要求,曲线表达式为:

Y=n0X5+n1X4+n2X3+n3X2+n4X+n5

(22)

φ=m0X5+m1X4+m2X3+m3X2+m4X+m5

(23)

式中:mi和ni(i=0,1,…,5)为多项式系数.

2.3 漂移控制器

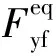
表1 车辆参数

由图3可知,车辆系统存在3种平衡状态:左转向漂移平衡态(红色三角形)、右转向漂移平衡态(蓝色圆形)和稳态转向平衡态(黑色星形).

(a)后轮驱动力 (b) 质心侧偏角 (c)横摆角速度

(d)前轮侧向力 (e)后轮侧向力图3 平衡态处状态参数随前轮转角变化曲线Fig.3 Change curve of state parameters at equilibrium with front wheel angle

图3(a)为后轮驱动力变化曲线,稳态转向过程中,后轮驱动力随前轮转角的增大而增大,但数值整体偏小;直至前轮转角达15°左右,轮胎达到附着极限(由图3(d)和图3(e)知,此处轮胎侧向力已接近饱和),前轮无法提供更大的侧向力,继续增大前轮转角会导致侧滑现象.此时,若减小前轮转角且反向增大,并控制后轮驱动力随前轮转角线性增大,车辆将进入漂移平衡态.由图3(b)和图3(c)可知,当车速恒定时,稳态转向下质心侧偏角变化范围较小,数值接近0;而横摆角速度随前轮转角的增大线性增长,车辆实际转向与前轮转向保持一致.漂移平衡点处质心侧偏角变大,说明此时车身姿态发生较大偏转.为了抑制车辆过度转向,前轮转角开始与横摆角速度反向来维持漂移状态,即方向盘反打现象.

由图3(d)和图3(e)可知,稳态转向过程中,前、后轮侧向力均处于饱和值内,符合车辆稳态运动特点.进入漂移状态后,由于后轮驱动力急剧增长,后轮完全饱和,前轮侧向力接近饱和状态,剩余侧向力用于调整车辆姿态.漂移平衡点的变化体现出漂移过程3大特点:大的质心侧偏角、方向盘反打和后轮饱和.

为保证车辆漂移过程中的安全性,要求车辆尽可能沿着参考路径漂移,即达到参考漂移半径R0:

图4 漂移半径有效区域Fig.4 Effective area of drift radius

在纵向车速为10 ～25 m/s 的范围内,求解前轮转向约束限制(-30°～30°)下的所有漂移平衡点,经过数据拟合可得到漂移平衡点与路径半径R0和纵向车速Ux的函数关系.此外,该车速范围内漂移半径有效区域如图4所示.(R0min,R0max)为当前纵向车速Ux下漂移半径有效区间,随着纵向车速的增大,漂移半径及漂移半径有效区间范围逐渐增大.

在漂移平衡点处,对车辆动力学方程式(3)作线性化处理,构建基于偏差的动力学方程:

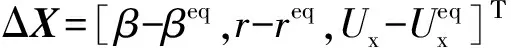
基于偏差动力学方程,定义漂移控制目标函数:

(27)

式中,Q3和R3分别为所设状态量偏差和控制量偏差的权重矩阵.

求解黎卡提方程,得到控制量ΔU:

PS+AΤP-PBR-1BΤP+Q3=0

(28)

前馈控制量Ueq和反馈控制量ΔU相结合生成控制量U:

车辆模型的实际输入量为前轮转角δf,由前轮侧向力Fyf通过式(4)映射得到.

2.4 车辆运动综合控制

控制系统结构如图5所示,包括车辆路径跟踪、局部避障和漂移.根据期望路径曲率k,判断当前道路是否处于漂移半径有效区间(R0min,R0max):

1)若不满足漂移条件,启动路径跟踪控制器,车辆沿期望路径行驶.行驶途中若遇到障碍物,在其进入控制器预测范围后,避障控制器规划出局部路径输给路径跟踪控制器,实现避障任务.

2)若具备漂移条件,即能够进行漂移过弯运动,则在指定漂移区域完成漂移.

图5 车辆控制系统结构Fig.5 Structure of vehicle control system

3 仿真实验与结果分析

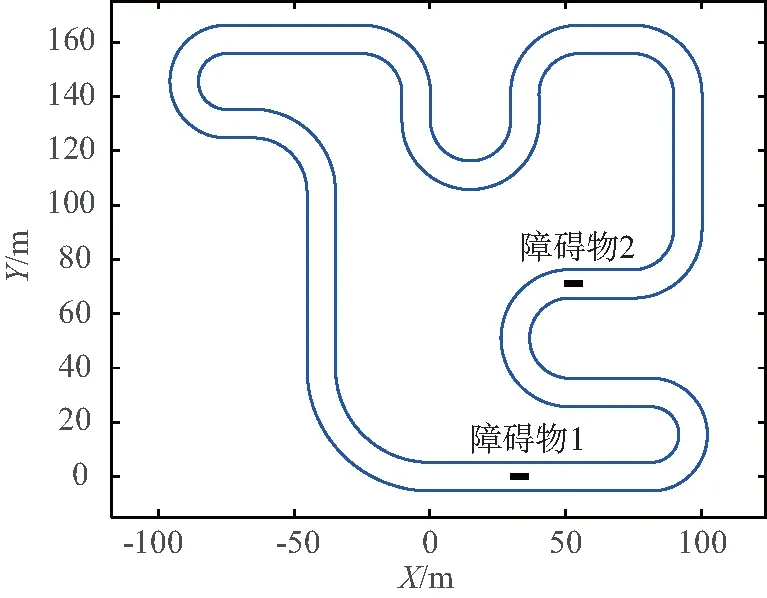
图6 封闭道路场景Fig.6 Closed road scenario

为验证所设计控制器的有效性,构建由多段直道、弯道衔接而成的复杂道路场景.考虑车辆避障时的变道空间,道路宽度设为 10.5 m(3车道宽度之和),路面附着系数μ为0.85.在道路中设置两处障碍物,大小均为 6 m×1.5 m 的矩形物,其质心位置分别为(33,0)和(53,71),场景如图6所示.

设置车辆初始位置为(0,-1.5),车辆质心侧偏角、横摆角速度和纵向车速的初始值分别为 0 deg、0 rad/s 和 10 m/s,并选择在道路左上角和右下角两处弯道进行漂移运动.基于Matlab软件对该控制器进行仿真验证,控制器参数如表2所示,仿真结果如图7～图9所示.

表2 控制器参数

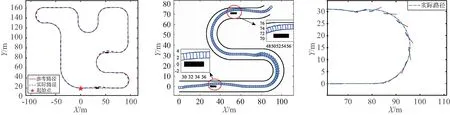
图7 参考路径和实际路径对比图8 行驶过程中车身轮廓包络线图9 漂移路段车辆位姿变化 Fig.7 Comparison between reference Fig.8 Body contour envelope Fig.9 Change of vehicle position path and actual path during driving and posture in drift section

车辆参考路径和实际行驶路径对比结果如图7所示.除避障运动外,车辆整体路径跟踪效果较好.车辆避障运动过程中的车身轮廓包络线如图8所示.在障碍物附近,车辆沿所规划的局部避障路径行驶,与障碍物和道路边界的间隙均大于安全阈值 0.2 m,两处均安全地完成避障任务,在避障结束后迅速回到参考路径上.所设计的两处漂移弯道相似,在此仅对第一个漂移过弯运动进行分析.图9为漂移路段车辆的位姿变化情况,蓝色点画线为实际行驶路径,矩形块表示前、后等效车轮,黑色表示轮胎受力未饱和,红色表示轮胎受力饱和.车辆路径跟踪过程中,前、后轮均未饱和,轮胎力处于稳定域范围内;车辆漂移过弯时,后轮会逐渐进入饱和状态,质心侧偏角出现较大偏转,前轮反方向转动,具备明显的漂移特征.

车辆运动过程中,控制量和状态量部分变化曲线如图10所示.图中仅显示车辆从初始位置出发至第一次漂移结束期间的参数变化.

图10(a)和图10(b)分别为前轮转角和后轮驱动力变化曲线.由于存在初始位置偏差和障碍物,在路径跟踪控制器的作用下,前轮转角产生小幅变化,实现避障并迅速接近参考路径;此时处于稳态转向,后轮驱动力较小.在 8 s 左右,开始第一次漂移过弯,后轮驱动力不断增大,迫使车辆进入极限漂移状态;在此期间,为保持左转弯行驶,前轮转角逐渐变大;当后轮驱动力接近漂移平衡态参考值时,后轮进入极限饱和状态,为了抑制车辆出现过度转向情况,前轮转角出现“反打”现象.

由图10(c)、图10(d)和图10(e)可知,稳态转向时,质心侧偏角和横摆角速度与前轮转角呈现一致的变化趋势,且质心侧偏角几乎为0,车速相对稳定,均符合稳态转向特点.在 8 s 左右,受后轮驱动力突然增大的影响,纵向车速和质心侧偏角均出现短暂增长,横摆角速度迅速增大.随着后轮逐渐饱和、方向盘反打程度的加深,质心侧偏角开始减小且反向增长,车身姿态发生较大偏转;纵向车速和横摆角速度小幅超调后,不断趋近于参考值;横摆角速度始终为正值(左转弯),与实际转向情况相一致.直至 12 s 左右,所有状态量均稳定在参考值附近,车辆完全进入稳态漂移,成功实现第一次漂移过弯;出弯后,继续进行路径跟踪,完成后续的行驶.