执行功能在不同年级儿童数学能力中的作用*

祝孝亮 赵 鑫

执行功能在不同年级儿童数学能力中的作用*

祝孝亮 赵 鑫

(甘肃省行为与心理健康重点实验室; 西北师范大学心理学院, 兰州 730070)

选取812名三～六年级的儿童, 采用相关分析和结构方程模型等方法考察了各执行功能成分在不同年级儿童三种数学能力中的作用。结果显示, 在低年级阶段, 工作记忆广度是数学运算能力、空间想象能力和逻辑思维能力最重要的预测因素; 在高年级阶段, 工作记忆广度对三种数学能力的预测作用下降, 而工作记忆刷新和认知灵活性对数学能力的预测作用提升。这表明, 各执行功能成分对不同数学能力的预测作用存在差异, 并将随儿童年级的增长而发生变化。

执行功能, 数学能力, 小学儿童, 结构方程模型

1 引言

数学能力是指个体顺利而有效的完成数学活动、解决数学问题的个性心理特征(文萍等, 2007), 主要受领域特异性因素(如近似数量系统)和领域一般性因素(如执行功能)的影响(Halberda et al., 2008; Yang et al., 2019)。近年来, 越来越多的研究者致力于揭示数学能力与数学学习的基本认知和感知机制, 尤其是执行功能在儿童数学学习中的作用(Espy et al., 2004; Spiegel et al., 2021)。这是因为在进行数学任务时个体需要忽视无关信息和抵制分心刺激, 在各种操作和解题策略间灵活转换以及存储与操纵数字相关的信息, 而这些认知过程与执行功能均存在密切联系(Bull & Lee, 2014; Duncan et al., 2017; Wang et al., 2019)。

作为一种高阶的认知功能, 执行功能是指对完成目标导向行为至关重要的一系列认知能力(Camerota et al., 2020; Diamond, 2013), 主要包括抑制控制、工作记忆和认知灵活性三个核心成分。横断与纵向研究的证据表明, 执行功能是数学能力显著的预测因子(Ahmed et al., 2019; Kahl et al., 2021; Magalhães et al., 2020), 具有良好执行功能的个体在学习环境中可以更好的计划、维持注意力、记忆, 从而获得更多的学习机会来提升数学技能(Rutherford et al., 2018), 这致使部分研究将执行功能作为提升儿童数学能力的潜在干预目标(Blakey et al., 2020; Wang et al., 2019)。然而, 以往研究所得出的执行功能子成分与儿童数学能力之间的联系并不一致。如研究发现, 抑制控制是数学能力最有力的预测因子, 是决定儿童数学能力高低的核心认知因素(Bull & Scerif, 2001; Espy et al., 2004; Peng et al., 2012), 但亦有研究表明, 抑制控制对数学能力影响较小或抑制控制无法有效预测儿童的数学能力(Georgiou et al., 2020; der Ven et al., 2012; Dekker et al., 2017)。同时, 工作记忆和认知灵活性与儿童数学能力的关系也显现出研究结论的不一致。部分学者发现, 工作记忆(Ahmed et al., 2019; Monette et al., 2011)或认知灵活性(Magalhães et al., 2020)是执行功能成分中预测儿童数学能力的唯一因子。然而, 也有研究表明, 相比于其他执行功能成分, 工作记忆或认知灵活性与数学能力之间的联系较小(Cantin et al., 2016; Ellefson et al., 2020; Zhang et al., 2018)。这说明, 执行功能与儿童数学能力间的实质联系仍需进一步探究。

1.1 执行功能子成分与不同数学能力之间的关系

在以往研究中, 对于执行功能和儿童数学能力关系的考察要么将执行功能当作一个整体(Fung et al., 2020), 要么分别考察了执行功能的三个成分(抑制控制、工作记忆和认知灵活性)与数学能力的关系(Nguyen & Duncan, 2019), 多数研究由于并未系统考虑到执行功能子成分的可再分性, 从而导致执行功能与数学能力关系的研究结论显现出不一致。对于抑制控制而言, 一般可将其划分为反应抑制和干扰抑制(Diamond, 2013), 其分别侧重于抑制不恰当的行为与保持良好的注意力控制(赵鑫等, 2016; Diamond, 2013)。如研究发现, 学龄儿童干扰抑制与数学能力之间的相关程度较低或学龄儿童的干扰抑制无法有效预测其数学能力(Cragg et al., 2017; Lee et al., 2018), 而反应抑制可以显著预测学龄儿童的数学能力(St Clair-Thompson & Gathercole, 2006; Sulik & Obradović, 2018)。针对工作记忆, 尽管已有研究发现工作记忆广度和工作记忆刷新密切相关(Friso-den Bos et al., 2013), 但二者又彼此独立, 代表着工作记忆的不同方面(Cirino et al., 2018; Himi et al., 2021; McKenna et al., 2017), 其在加工数学任务的过程中扮演着不同的角色(Friso-den Bos et al., 2013)。如工作记忆广度侧重于对任务相关信息的存储和加工, 尤其在计算任务上(Cragg et al., 2017); 而工作记忆刷新则更强调对数学任务中部分信息的更新或替换(Archambeau & Gevers, 2018), 在解决逻辑推理问题时发挥的作用更大(Holmes et al., 2009)。因此, 在考察执行功能与儿童数学能力的关系时, 若缺少对抑制控制与工作记忆不同方面的考虑, 将更易产生研究结论不一致的争议。

同时, 多数研究在考察不同执行功能成分与儿童数学能力的关系时缺乏考虑数学能力的多维性。如研究发现, 抑制控制对儿童数学代数不起独立的预测作用(Lee et al., 2018), 但可以显著预测儿童在计数任务上的表现(Cueli et al., 2020); 工作记忆与算术运算间的联系较低, 而与应用问题解决之间的关系更为紧密(Spiegel et al., 2021); 相比于数学运算, 认知灵活性和数学推理间的联系更加密切(Georgiou et al., 2020)。可见, 不同执行功能成分与不同数学技能间的联系存在差异, 对执行功能与数学能力间关系的探讨应考虑数学能力的多维性。迄今为止, 关于数学能力的组成部分, 研究者们的观点仍未统一。如国外研究者指出, 学龄儿童的数学能力主要包括运算、代数、几何与测量(Spiegel et al., 2021), 或运算、代数和几何(Gilmore et al., 2015)。而国内研究者及小学数学教学大纲通常将学龄儿童的数学能力划分为：数学运算能力、逻辑思维能力和空间想象能力(杜文平, 2013; 林崇德, 2011; 吴汉荣, 李丽, 2005)。基于此, 本研究继续沿用国内学者对学龄儿童数学能力的分类, 将小学儿童的数学能力分为：数学运算能力、逻辑思维能力与空间想象能力, 以期探究执行功能各子成分在不同数学能力中的作用。

研究发现, 工作记忆广度是数学认知发展最有力的预测因子(Viterbori et al., 2017; Hilbert et al., 2019), 尤其在计算和空间等数学任务上(Friso-den Bos et al., 2013)。语音表征假说认为, 解决计算问题需要在短时记忆中编码和维持语音表征, 并从长时记忆中提取语音编码(Holmes et al., 2021), 存在计算障碍的儿童由于其工作记忆广度较小, 导致工作记忆中信息的衰竭速度较快, 提取数学事实的错误率较高(Toll et al., 2011), 从而影响儿童计算问题的解决。相关研究也表明, 工作记忆广度是影响儿童解决简单和复杂计算问题最重要的因素(Chen & Bailey, 2021; Cragg et al., 2017)。同时, 工作记忆广度还有助于儿童解决空间几何问题(Passolunghi et al., 2008), 这是因为空间几何问题的加工不仅需要在大脑中对几何体的直观形象做出表征, 还需要对表征的结果进行维持, 直到问题完全解决(Friso- den Bos et al., 2013)。这些发现为工作记忆广度直接影响运算和空间等数学问题的解决提供了有力支持。研究发现, 工作记忆刷新对于更加复杂和不熟悉的数学任务具有最大的预测力(Clements et al., 2016; Jenks et al., 2012)。如在解决逻辑推理问题时, 儿童需要在工作记忆中对所呈现的文本信息进行加工、编码, 从而形成有关问题结构的心理图示, 在解题过程中, 需要不断对可能的答案进行比较和更新, 使原有的心理图示加强或改变, 而这则与工作记忆刷新能力有关(Holmes et al., 2009; Peng et al., 2018; Spiegel et al., 2021)。此外, 研究表明, 抑制控制(干扰抑制与反应抑制)与计数和周长比较(几何)等数学问题更为有关(Jiang et al., 2019; Lan et al., 2011), 在运算和逻辑推理等数学任务中有较少的参与(Harvey & Miller, 2017; Yang et al., 2019)。还有研究表明, 认知灵活性对需要多步骤运算的复杂数学问题存在较大影响(Bull & Lee, 2014; Bull & Scerif, 2001), 而在加、减法等简单算术中发挥的作用有限(Cantin et al., 2016; Georgiou et al., 2020)。这说明, 不同执行功能成分在不同数学能力的发展过程中所起的作用存在差异。

1.2 执行功能子成分与数学能力关系的变化

此外, 已有研究较少考虑年龄对执行功能与儿童数学能力关系的影响。研究发现, 随着儿童年龄的增长, 所使用的数学策略和掌握的数学技能更加熟练与自动化, 支持数学加工的特定脑区日益凸显,这将导致儿童在加工数学任务时降低对于低阶执行功能资源的需求(Cragg & Gilmore, 2014; Peng et al., 2018; Stipek & Valentino, 2015)。例如, Geary (2004)发现, 对基本数学事实的自动检索将致使工作记忆广度较少参与大龄儿童解决简单的运算问题; Cantlon等人(2009)使用功能性磁共振成像(fMRI)考察了儿童与成人在进行计算任务时脑皮层激活的差异, 结果显示, 儿童主要激活额叶区域, 而成人在后顶叶区域表现出更大程度的激活; Bryce等人(2015)的横断研究表明, 抑制控制与数学推理能力之间的联系在低龄儿童中更为紧密。这说明随着年龄的增长, 个体在进行数学任务时将减少对工作记忆广度和抑制控制的需求。对此, “淡出”假说(“Fade-out” Hypothesis)指出, 随着年龄的增长, 大龄儿童在进行数学任务时对工作记忆广度和抑制控制的依赖下降, 即更加基础的认知能力在数学任务中发挥的作用会更低(Stipek & Valentino, 2015)。然而, 在小学高年级阶段, 高阶的执行功能(如, 认知灵活性和工作记忆刷新)会得到较大发展(王晓芳等, 2011; Fisk & Sharp, 2004; Magalhães et al., 2020; Wang & Zhou, 2019), 其将取代抑制控制和工作记忆广度等更为基础的执行成分, 成为支持儿童数学能力发展的主要认知因素(Clements et al., 2016; Ellefson et al., 2020; der Ven et al., 2012)。如Magalhães等人(2020)发现在控制了流体智力、注意、抑制控制、工作记忆和计划后, 认知灵活性是预测小学高年级儿童数学能力的唯一因子。研究还发现, 相比于工作记忆广度, 工作记忆刷新更能预测高年级儿童是否存在数学学习困难(St Clair- Thompson & Gathercole, 2006)。可见, 不同执行功能成分与儿童数学能力的关系会随儿童年龄的增长而发生改变, 低阶执行功能成分是支持低龄儿童数学能力发展的重要因子, 而高阶执行功能成分则是预测大龄儿童数学能力的核心认知因素。

1.3 研究假设与内容

如前所述, 执行功能在支持儿童数学能力发展的过程中发挥着重要作用。但目前较少有研究系统探究各执行功能成分在儿童不同数学能力(数学运算能力、逻辑思维能力与空间想象能力)中的作用, 以及这种影响模式是否会随儿童年级阶段的不同而显现出差异。基于上述分析, 我们假设不同执行功能成分在不同数学能力中起到的作用存在差异, 具体来说, 工作记忆广度是数学运算能力和空间想象能力的重要预测因素; 而工作记忆刷新则更能预测儿童的逻辑思维能力; 干扰抑制、反应抑制和认知灵活性在数学运算能力、空间想象能力和逻辑思维能力中的作用相对较低。同时, 鉴于年龄在执行功能与数学能力关系中的作用, 我们假设不同执行功能成分对不同数学能力的预测会随儿童年级的升高而发生改变。具体而言, 随着年级水平的升高, 低阶执行功能成分(干扰抑制、反应抑制、工作记忆广度)在数学能力中的作用会逐渐降低, 而高阶执行功能成分(工作记忆刷新、认知灵活性)对数学能力的预测作用将逐渐增大。

与前人研究相反, 本研究主要关注于小学中高年级的儿童, 其原因主要分以下三点：第一, 选取学龄中高年级的儿童将降低由于缺乏数学指导而导致数学成绩较差的风险。第二, 这些儿童在数学能力的发展上已经超越了简单计算, 其逻辑思维和空间想象等数学能力获得了较大发展, 因而兼具了不同的数学能力。第三, 儿童各执行功能子成分已获得了进一步发展(Lehto et al., 2003)。基于于萍和左梦兰(1996)的研究, 三～六年级儿童的数学能力会随年级的增长而逐渐提高, 即三、四年级儿童处于具体运算阶段, 对数学问题的加工是一种双重协调的过程; 而五、六年级儿童的抽象推理能力获得较大发展, 对数学问题的加工则转向精致协调。由此, 对学龄中高年级儿童进行考察将更清晰的刻画出各执行功能成分与不同数学能力间的实质联系。因此, 本研究将通过一系列任务考察三至六年级儿童在各执行功能子成分和不同数学能力上的表现, 通过对各任务间关系的分析来验证本研究的假设。在控制了年龄和性别的影响后, 我们构建了本研究的假设理论模型, 如图1所示。

2 方法

2.1 被试

本研究以4所小学的825名三～六年级小学生为研究对象, 由于13名学生未完成所有的测验, 在数据分析阶段予以剔除, 最终有效人数共812人, 其中, 男生390人, 女生422人, 年龄范围为8～14岁, 平均年龄为10.46岁(= 1.22), 各年级被试基本情况详见表1。4所小学在校园环境水平(教师教学水平、学校基础设施)上大致相同。所有被试均为健康儿童, 排除存在发展障碍的儿童(如, 听障、ADHD和智力发育迟滞), 儿童参与实验均得到了家长和班主任老师的知情同意, 在实验结束后给予了一定的报酬。

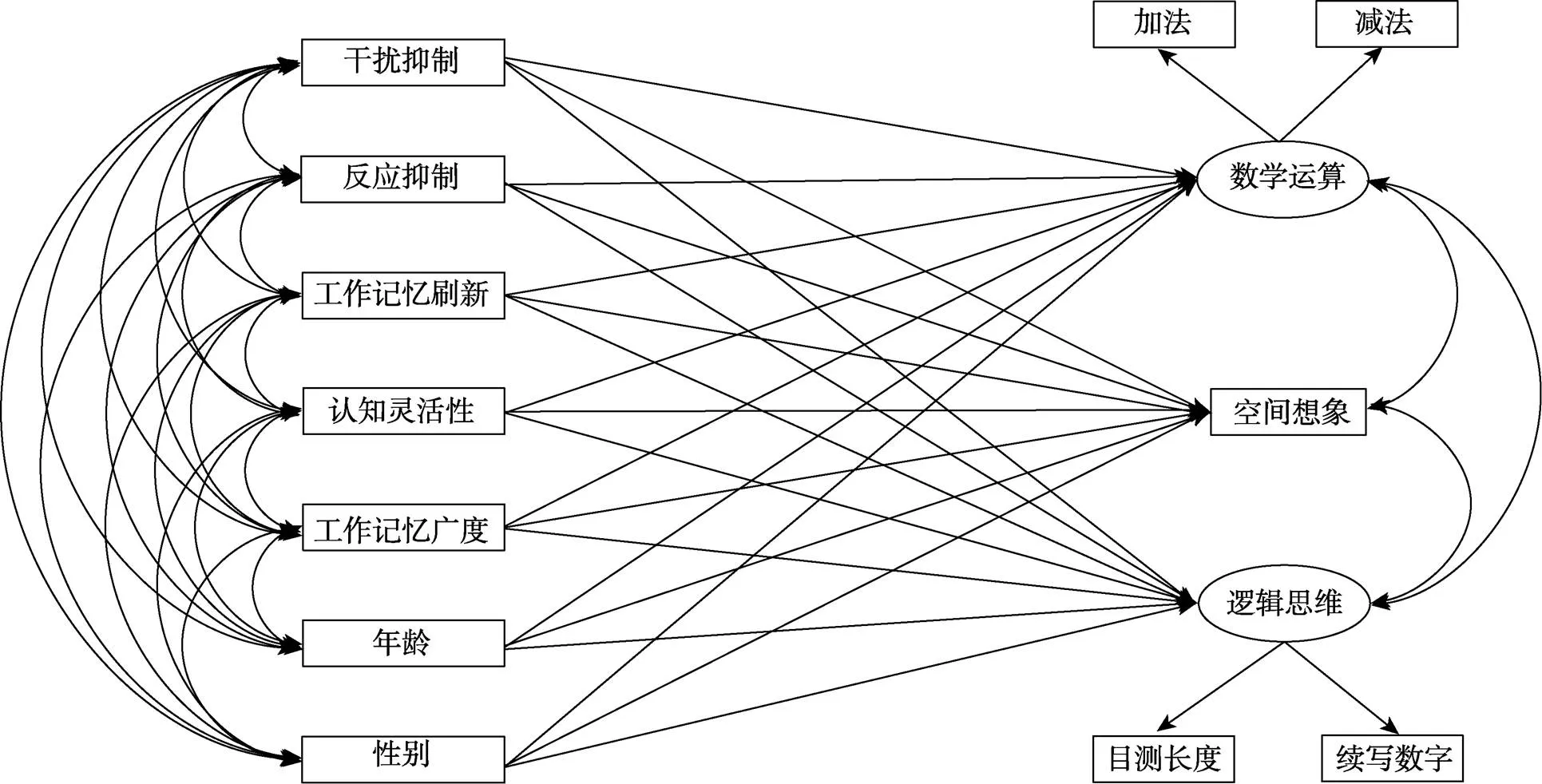
图1 各执行功能成分与不同数学能力关系的假设理论模型

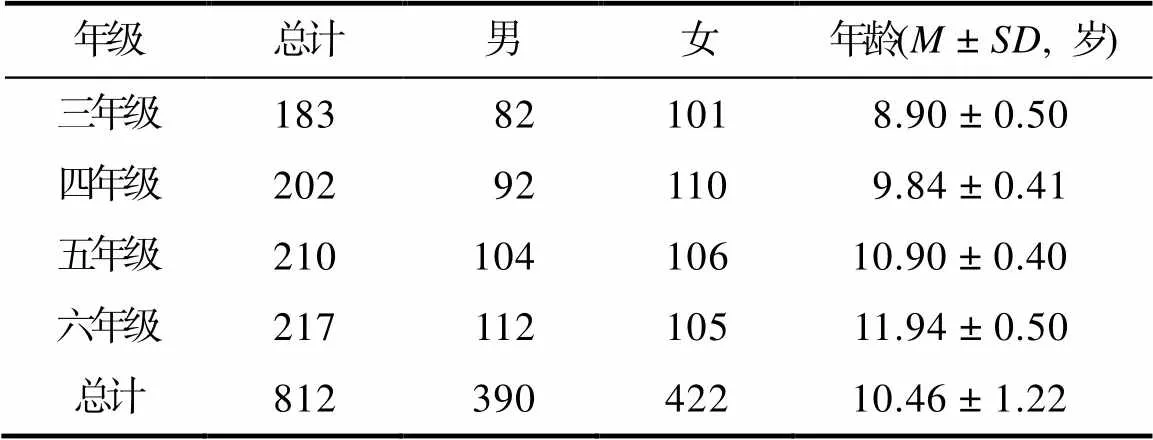
表1 被试人口学变量

2.2 测验工具

2.2.1 数学能力

本研究选用德国海德堡大学编制的小学生数学基本能力测试量表的中国修订版(吴汉荣, 李丽, 2005)中的6个分测验来考察儿童的数学能力。该量表原始共包含两个分量表, 共12个分测验。其中, 数字抄写为热身任务, 目的是让学生掌握测试方式与测试环境, 不计入量表分值计算; 数学运算分量表由加法、减法、乘法、除法、比较大小和填空等分测验组成, 用以评估学生的数学概念、运算速度及计算准确性; 逻辑思维与空间−视觉功能分量表由续写数字、目测长度、方块计数、图形计数和数字连接等分测验组成, 用以衡量学生的数学逻辑思维、规律识别、空间立体思维和视觉跟踪能力。如前文所述, 学龄儿童的数学能力主要包括数学运算能力、逻辑思维能力及空间想象能力。基于儿童实际掌握的数学知识和准确评估所考察的数学能力, 我们选取了该量表中的6个分测验用以评估儿童数学能力的三个方面。在本研究中, 数字抄写任务用于儿童了解测验形式, 为热身任务。在正式测验中, 使用该量表中的加法和减法分测验来衡量儿童的数学运算能力; 使用续写数字与目测长度分测验来评估儿童的逻辑思维能力; 使用方块计数分测验来考察儿童的空间想象能力。该量表原始的内部一致性信度系数为0.7以上, 分半信度为0.83, 矫正信度为0.90, 效度指标也均达到统计学标准。各测验的计分方式为每对1题, 记为1分, 总分越高, 代表被试相应的数学能力越高(吴汉荣, 李丽, 2005)。具体分测验如下。

(1)数学运算能力

加法分测验与减法分测验各包含40个题项, 用于考察儿童数学运算的速度及准确性。在每个分测试中, 要求儿童在1分钟之内尽力做出最多的题项, 题目难度从个位数的加减法(如, 7 ± 3 = ?)到百位数的加减法(如, 452 ± 113 = ?)逐渐递增, 做对1题记1分, 分数越高, 表示儿童的运算能力越好。

(2)逻辑思维能力

使用续写数字与目测长度分测验来评估儿童的逻辑思维能力。其中, 续写数字分测验共含有20个题项, 该测验要求儿童根据每个题项中已知的6个数字去推论随后应出现的3个数字, 做对一题记1分; 目测长度分测验共包含24个题项, 要求儿童根据本测验起始部分给出的3条带长度的线段来判断每个正式题项中线段的长度, 做对1题记1分。两个测验正式施测的时间均为3分钟, 题目难度逐步提升, 分数越高, 代表儿童的逻辑思维能力越好。

(3)空间想象能力

使用方块计数分测验来考察儿童的空间想象能力。该测验共包含28个项目, 要求儿童判断每个题项所示的空间立体图形由多少个小正方体构成, 每做对1题记作1分。整个测验限时3分钟。题目难度逐渐递增, 分数越高, 代表儿童的空间想象能力越好。

2.2.2 中央执行功能测验

(1) Stroop任务

采用Stroop任务来考察被试的干扰抑制能力(Zhao et al., 2018), 在该任务中, 实验材料由两个表示颜色的汉字(“红”和“绿”)和一个无意义字符串(“####”)所组成, 要求被试根据所呈现汉字或字符串的颜色做出相应的按键反应, 红色按“F”键, 绿色按“J”键。该任务总共包括三种条件：一致条件(红色的“红”字和绿色的“绿”字)、不一致条件(红色的“绿”字和绿色的“红”字)和中性条件(红色的“####”和绿色的“####”)。在每个block开始时, 屏幕中央会呈现一个持续500 ms的注视点“＋”, 随后是1000 ms的空屏, 接下来呈现1500 ms的刺激, 刺激之后空屏, 进入下一个试次。该任务共包括1个练习block和3个正式实验的block, 其中练习block是为了让被试熟悉实验流程, 共包含18个试次, 当被试的正确率达到85%以上方可进入正式实验。在正式实验的3个block中, 每个block都包括一致、不一致和中性三种条件, 每种条件包括12个试次, 每个block下总共36个试次, 整个正式实验包括108个试次。该任务主要记录的数据指标为不一致条件、一致条件、中性条件下的平均反应时及干扰效应, 其中干扰效应等于不一致条件下的平均反应时减去中性条件下的平均反应时。整个实验大约需要15分钟, 被试可以在每个block间进行休息。

(2) GO/NOGO任务

采用GO/NOGO任务来考察被试的反应抑制能力(Zhao et al., 2018)。在该任务中, 被试需要对呈现的GO刺激进行按键反应, 对NOGO刺激不做反应, GO刺激和NOGO刺激呈现的比率各占50%。该任务共包含2个练习block (每个block包含10个GO试次和10个NOGO试次)和4个正式实验block (每个block包含50个GO试次和50个NOGO试次)。在每个block开始时, 屏幕中央会呈现一个持续1000ms的注视点“＋”, 随后呈现600 ms的刺激, 刺激之后空屏, 进入下一个试次。在正式实验的4个block中, 其中两个block是出现字母X按“J”键(GO试次), 出现字母Y不反应(NOGO试次), 另外两个block则与之相反(出现字母Y按“J”键)。这两种情况下都包括一个让被试熟悉实验流程的练习block, 当被试的正确率达到85%以上方可进行正式实验, 整个实验时间大约需要15分钟。

(3) 数字刷新任务

采用数字刷新任务对被试工作记忆中刷新信息的能力进行考察(Zhao et al., 2018)。数字刷新任务包括简单任务和困难任务两种, 简单任务中每个数字呈现的时间是1750 ms, 困难任务中每个数字呈现的时间是750 ms。被试先完成简单任务, 再完成困难任务。在整个任务中, 首先给被试随机呈现0～9的一系列数字, 数字的系列包括 5、7、9和11四个长度。每个系列的数字都是一个一个呈现, 要求被试不断的复述出现的数字并且按顺序记住最后出现的3个数字。例如, 屏幕上会依次出现6、8、5、4、7、2, 被试需要不断记忆6～68～685～854～ 547～472, 被试需要记住最后3个数字, 并把它们输入屏幕的黑色框内然后按空格键进入下一个系列。简单任务中总共包括1个练习block和两个正式实验的block, 练习block包括8个试次, 每种长度随机出现2次, 正式实验的每个block包括12个试次, 每个数字长度随机出现3次。在困难任务中, 总共包括2个block, 每个block包括12个试次, 每个数字长度随机出现3次。简单刷新任务和困难刷新任务的平均正确率作为刷新能力的指标。完成整个任务大约需要20分钟, 被试可以在每个block间进行休息。

(4) 数字正背和数字倒背

参照维克斯勒智力测验中的数字广度测验, 我们采用数字正背和数字倒背任务来评估被试的工作记忆广度能力。在数字正背任务中, 首先给被试随机呈现0～9的一系列数字(每个数字呈现1000 ms), 被试需要按照看到的顺序将数字依次输入屏幕中央的方框, 如被试看到1-2-3, 则需要输入1-2-3。实验任务难度从记忆3个数字开始, 每个难度有3次机会, 若被试回答正确两个试次及以上, 记忆项目增加1; 否则, 任务结束。在倒背任务中, 仍是给被试随机呈现0～9的一系列数字(每个数字呈现1000 ms), 被试需要将看到的数字按相反的顺序依次输入屏幕中央的方框, 如被试看到1-2-3, 则需要输入3-2-1。实验任务难度从记忆3个数字开始, 每个难度有3次机会, 若被试回答正确两个试次及以上, 记忆项目增加1; 否则, 任务结束。这两个任务的指标均为被试的最大记忆广度。

(5) 数字转换任务

采用数字转换任务来考察被试的认知灵活性(Zhao et al., 2018)。在该任务中, 被试将看到1～9的数字(不包括5), 当数字是红色时, 需要判断数字是大于5还是小于5 (任务A); 当数字是蓝色时, 需要判断数字是奇数还是偶数(任务B)。该实验共包含两种条件, 分别为执行单一任务(只执行任务A或任务B)和执行混合任务(同时执行任务A和任务B)。在任务A中, 被试需要将依次呈现的1～9 (除了5)的红色数字与5作比较, 大于5时按“A”键, 小于5的按“L”键; 在任务B中, 被试需要对依次呈现的1～9(除了5)的蓝色数字做出奇偶性判断, 奇数数字按“A”键, 偶数数字按“L”键。在正式实验开始前, 有两个单一任务的练习block用于被试熟悉实验流程, 当被试的正确率达到75%以上方可进入正式实验。正式实验由20个block组成, 包含10个单一任务block和10个混合任务block, 单一任务和混合任务随机呈现, 其中, 每个单一任务的block含有8个试次, 每个混合任务的block含有17个试次, 整个正式实验过程总共包括250个试次。整个实验过程大约需要20分钟, 被试可在每个block间休息。该任务的统计指标为单一试次、非转换试次和转换试次的平均反应时, 以及转换代价和混合代价, 转换代价等于转换试次的平均反应时减去非转换试次的平均反应时; 混合代价等于混合任务中非转换试次的平均反应时减去单一任务条件下的平均反应时。

2.3 研究程序

以班级为单位对儿童的数学能力进行考察, 对812名三～六年级的儿童分别进行加法、减法、续写数字、目测长度和方块计数等数学能力测验, 所有测试均为集体施测, 每班均由两名主试负责, 一名主试负责讲解各测验的任务要求, 另一名主试负责计时, 这些测验均在学生各自的教室内完成。随后, 以班级为单位, 分连续两天共3次在学校安静的微机室完成所有测量执行功能的任务。本研究数据收集、筛查和整理录入均来自于心理学专业的研究生, 所有人员在测验前均接受了专业的培训, 熟悉整个测验的流程和规则。

2.4 数据分析

使用SPSS 25.0对数据进行描述统计和相关分析, 通过Amos 23.0做结构方程模型的路径分析。

3 结果

3.1 描述统计与差异检验

表2显示的是各年级儿童在数学运算、逻辑思维、空间想象等数学能力及中央执行功能各任务上的平均数与标准差。同时, 对不同年级被试在各测验上的成绩进行了差异检验。由表2可知, 4个年级的儿童在衡量3个数学能力的各测验上均存在显著差异(s > 7;s < 0.001)。在中央执行功能方面, Stroop干扰效应在不同年级间存在显著差异,(3, 808) = 2.79,< 0.05, ηp2= 0.01, 四年级儿童的成绩显著高于三年级儿童的成绩(< 0.05)。NOGO正确率在年级上差异显著,(3, 808) = 5.55,< 0.01, ηp2= 0.02, 事后比较结果显示, 四至六年级儿童在NOGO正确率上的成绩显著高于三年级儿童。在衡量工作记忆刷新、工作记忆广度和认知灵活性的各任务上, 4个年级之间均存在显著差异(s > 19;< 0.001)。事后比较结果显示, 高年级儿童在各任务上的表现显著优于低年级儿童(s< 0.05)。

3.2 各执行功能成分与不同数学能力的相关分析

对所有被试性别、年龄、不同数学能力、各执行功能任务的成绩进行了相关分析(表3)。结果显示, 性别与运算成绩、空间想象成绩、反应抑制和工作记忆刷新均存在显著相关关系(s< 0.05)。除与干扰抑制之外, 年龄与其他变量均呈现显著相关关系(s< 0.05)。干扰抑制只与逻辑思维成绩呈显著正相关,(812) = 0.09,< 0.01, 反应抑制与三个数学能力均无显著相关关系(s> 0.05)。工作记忆刷新、工作记忆广度和认知灵活性与运算成绩、逻辑思维成绩和空间想象成绩之间均呈现显著正相关(s< 0.01)。

3.3 各执行功能成分与不同数学能力之间的结构方程模型

在描述统计及相关分析的基础上, 依据本研究的假设理论模型对结果进行检验。结果显示, 三～六年级阶段模型的各拟合指标良好：χ2/= 4.784, GFI = 0.983, CFI = 0.970, AGFI = 0.925, RMSEA = 0.068。标准化路径分析结果如图2所示, 在将年龄和性别作为控制变量后, 工作记忆刷新、工作记忆广度和认知灵活性与数学运算的路径系数均达到了显著性水平(γ = 0.22,< 0.001; γ = 0.24,< 0.001; γ = 0.08,< 0.05)。这表明, 相比于认知灵活性, 工作记忆刷新和工作记忆广度是预测数学运算最有力的因子。工作记忆刷新、工作记忆广度和认知灵活性与空间想象能力的路径系数均达到了显著性水平(γ = 0.18,< 0.001; γ = 0.17,< 0.001; γ = 0.10,< 0.01), 这说明工作记忆刷新、工作记忆广度和认知灵活性显著预测了儿童在空间想象成绩上的表现。工作记忆刷新、工作记忆广度和认知灵活性与逻辑思维成绩的路径系数均达到了显著性水平(γ = 0.35,< 0.001; γ = 0.25,< 0.001; γ =0.13,< 0.01), 这表明工作记忆刷新、工作记忆广度和认知灵活性是预测逻辑思维能力的重要认知因素。

表2 不同年级执行功能、数学能力各任务的平均值和标准差及方差分析结果

注：***< 0.001, **< 0.01, *< 0.05, 下同。

表3 三至六年级被试各执行功能成分与不同数学能力之间的相关分析(N = 812)

注：性别进行了哑变量处理, 0 = 女, 1 = 男, 下同。

图2 三～六年级阶段各执行功能成分与不同数学能力关系的结构方程模型

注：所有路径系数均为标准化系数, 单箭头直线代表预测关系, 双箭头曲线代表相关关系。实线代表显著的回归路径, 虚线代表不显著的回归路径, 图中只呈现了自变量相关系数达到显著水平的路径。下同。

3.4 不同年级阶段儿童的各执行功能成分与不同数学能力的相关分析

为进一步具体了解不同年级阶段儿童的各执行功能成分与不同数学能力的关系, 分别以三、四年级为一个年级阶段, 五、六年级为一个年级阶段, 对各任务的成绩做相关分析。结果如表4和表5所示。

表4是三、四年级阶段各执行功能成分与不同数学能力之间的相关分析结果。结果显示, 性别与运算成绩、空间想象成绩和反应抑制均存在显著相关关系(s < 0.05)。年龄与干扰抑制、工作记忆广度和认知灵活性均呈现显著相关关系(s < 0.05)。干扰抑制与逻辑思维成绩呈显著正相关,(385) = 0.14,< 0.01, 反应抑制与三个数学能力均无显著相关关系(s> 0.05)。工作记忆刷新、工作记忆广度与三个数学能力之间均存在显著正相关(s < 0.01)。认知灵活性只与逻辑思维成绩和空间想象成绩之间呈显著相关关系(s < 0.01)。

表5表示的是五、六年级阶段各执行功能成分与不同数学能力之间的相关分析结果。结果显示, 性别与反应抑制和工作记忆刷新存在显著相关关系(s< 0.05)。干扰抑制和反应抑制与三个数学能力均无显著相关关系(s> 0.05)。工作记忆刷新、工作记忆广度和认知灵活性与运算成绩、逻辑思维成绩和空间想象成绩之间均呈现显著正相关(s< 0.01)。

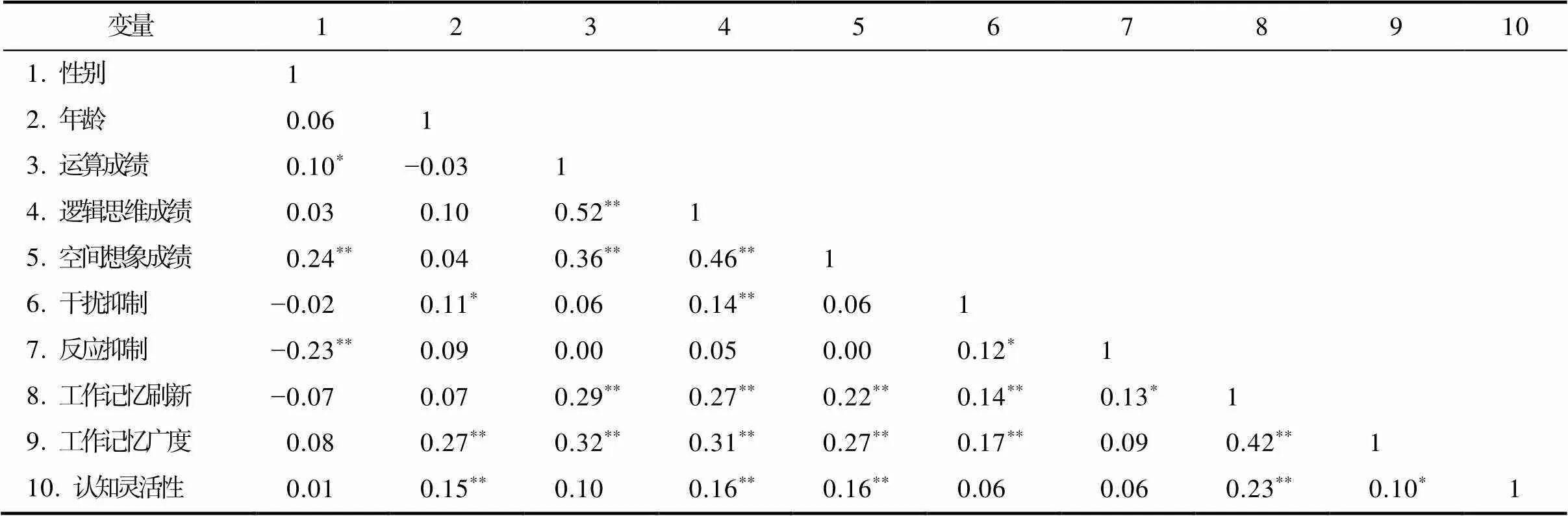
表4 三、四年级被试各执行功能成分与不同数学能力之间的相关分析(n = 385)

表5 五、六年级被试各执行功能成分与不同数学能力之间的相关分析(n = 427)

3.5 不同年级阶段儿童的各执行功能成分与不同数学能力关系的结构方程模型

为了进一步考察不同年龄阶段各执行功能成分对不同数学能力的影响, 依据本研究的假设理论模型对不同年级阶段被试的结果进行了检验。

在三～四年级阶段的结构方程模型中, 各拟合指标良好：χ2/= 2.716, GFI = 0.980, CFI = 0.965, AGFI = 0.913, RMSEA = 0.067。标准化路径分析结果如图3所示, 在将年龄和性别作为控制变量后, 工作记忆刷新和工作记忆广度与数学运算成绩的路径系数达到了显著性水平(γ = 0.21,< 0.001; γ = 0.28,< 0.001), 这表明工作记忆刷新和工作记忆广度对数学运算能力具有显著的预测作用。工作记忆刷新、工作记忆广度和认知灵活性与空间想象成绩的路径系数均达到了显著性水平(γ = 0.13,< 0.05; γ = 0.19,< 0.001; γ = 0.11,< 0.05), 这说明工作记忆刷新、工作记忆广度和认知灵活性可以显著预测儿童的空间想象能力。工作记忆刷新、工作记忆广度与逻辑思维成绩的路径系数达到了显著性水平(γ = 0.27,< 0.01; γ = 0.33,< 0.001), 这表明, 工作记忆刷新和工作记忆广度是预测儿童逻辑思维能力的有效认知因素。

在五～六年级阶段的结构方程模型中, 各拟合指标良好：χ2/= 1.547, GFI = 0.989, CFI = 0.988, AGFI = 0.954, RMSEA = 0.036。标准化路径分析结果如图4所示, 在将年龄和性别作为控制变量后, 工作记忆刷新、工作记忆广度和认知灵活性与数学运算的路径系数均达到了显著性水平(γ = 0.20,< 0.001; γ = 0.22,< 0.001; γ = 0.11,< 0.05)。这表明, 工作记忆刷新、工作记忆广度和认知灵活性是预测高年级儿童数学运算最有力的因子。工作记忆刷新、工作记忆广度和认知灵活性与空间想象成绩的路径系数均达到了显著性水平(γ = 0.20,< 0.001; γ = 0.15,< 0.01; γ = 0.10,< 0.05), 这说明工作记忆刷新、工作记忆广度和认知灵活性显著预测了儿童在空间想象能力上的表现。工作记忆刷新、工作记忆广度和认知灵活性与逻辑思维成绩的路径系数均达到了显著性水平(γ = 0.38,< 0.001; γ = 0.19,< 0.01; γ = 0.20,< 0.01)。这表明工作记忆刷新、工作记忆广度和认知灵活性是预测逻辑思维能力的重要认知因素。

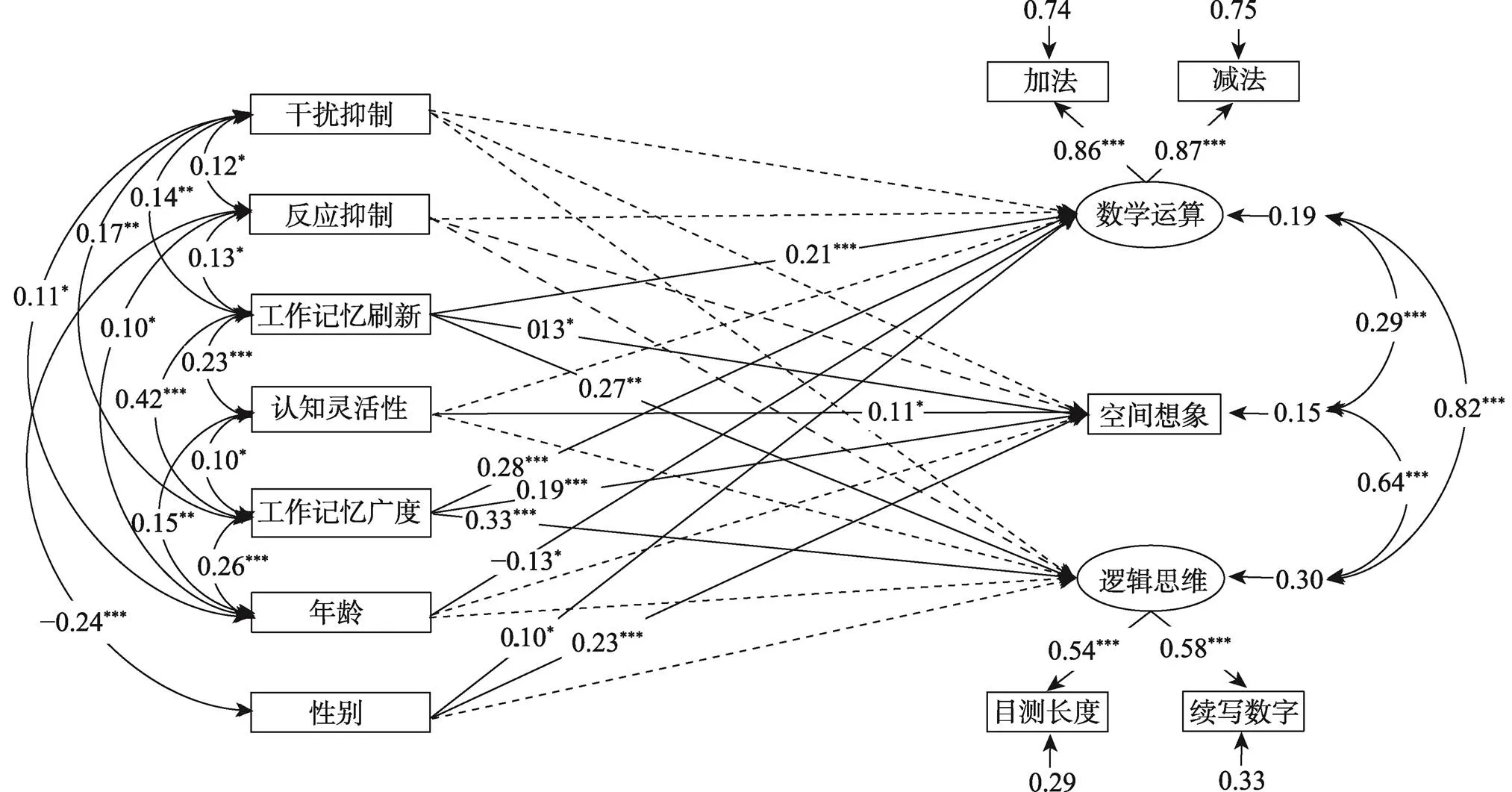
图3 三～四年级阶段各执行功能成分与不同数学能力关系的结构方程模型

图4 五～六年级阶段各执行功能成分与不同数学能力关系的结构方程模型

4 讨论

4.1 执行功能各成分在不同数学能力中的作用

本研究主要考察了各执行功能成分对学龄儿童不同数学能力的预测作用, 并进一步探讨了这种预测模式在不同的年级阶段是否存在差异。结果发现, 在控制了年龄和性别因素后, 各执行功能成分在数学能力中的作用会随数学能力的类型而发生变化。具体而言, 工作记忆广度是数学运算和空间想象显著的预测因子, 而工作记忆刷新则更能预测儿童的逻辑思维能力。

首先, 本研究证明, 工作记忆广度是预测儿童数学运算能力和空间想象能力的重要因子。在数学运算中, 简单计算往往与数学事实相对应, 其正确答案源于从长时记忆的联想网络中提取而非通过运算(Archambeau & Gevers, 2018)。当儿童从长时记忆中检索到相应的数学事实时, 工作记忆广度较大的儿童能更好的抵制无关干扰并选取正确信息(Miller-Cotto & Byrnes, 2020)。而在复杂的数学运算中(如, 258 + 386), 工作记忆广度主要参与多步骤问题中数字元素的临时存储与操作, 个体需要对该问题进行编码、执行大量的计算, 并将部分先得结果暂时存储(Raghubar et al., 2010), 因此, 执行复杂的计算问题严重依赖于个体的工作记忆广度。此外, 本研究还证实了工作记忆广度是预测空间想象能力的重要因素。在空间想象任务中, 儿童需要大量的工作记忆资源对空间几何体进行观察、分析, 并在大脑中生成相应的直观图, 而工作记忆广度对于这种心理表征显得非常重要。研究发现, 工作记忆广度更大的个体可以更为有效和清晰的表征任务材料(Miller-Cotto & Byrnes, 2020)。

其次, 研究发现, 工作记忆刷新在解决逻辑思维问题中发挥了更重要的作用。这或许是因为成功的解决逻辑思维问题不仅需要在工作记忆中暂时存储任务相关的背景信息, 还需要根据当前的任务要求对存储的信息不断进行更新, 以形成解决问题的新表征和心理图示, 因而需要更多的认知资源(Swanson, 2011)。如, 在解决逻辑推理问题(1, 3, 5, 7, 9, 11, )时, 儿童首先需要将已给出的数字维持在工作记忆中, 通过对其进行比较, 进而生成假设(奇数序列), 使问题得以正确解决。此外, 基于训练的研究结果也证实了工作记忆刷新与逻辑思维能力之间的关系。如, Holmes等人(2009)对10岁儿童进行了为期20天的工作记忆刷新训练, 发现6个月后儿童的数学推理能力具有显著的提升。

最后, 本研究结果显示, 认知灵活性对于儿童数学能力的预测力较小, 而抑制控制则不具有预测作用。在认知灵活性方面, 尽管大量研究考察了认知灵活性与儿童数学能力之间的联系, 但结论仍存在争议。如研究者发现, 认知灵活性对儿童完成简单的代数、数学运算及数学应用问题没有贡献(Georgiou et al., 2020; Lee et al., 2018; Toll et al., 2011)。而其他研究者则证明认知灵活性在儿童完成复杂的多步骤问题中发挥重要作用(Yang et al., 2019; Yeniad et al., 2013)。然而, 本研究所使用的数学任务较少涉及多任务、操作和思维模式之间的切换, 因而降低了认知灵活性在问题解决中的参与度。此外, 本研究还发现抑制控制(干扰抑制、反应抑制)与儿童数学能力的三个方面均没有关系, 这与以往部分研究的结果相一致(Toll et al., 2011; Yang et al., 2019)。如Toll等人(2011)考察了执行功能与数学学习困难之间的关系, 发现与工作记忆相比, 抑制控制对于准确的将数学学习困难个体分类出来没有贡献。从发展的视角来看, 抑制控制是个体执行功能成分中最早开始发展的认知能力(Best et al., 2009), 将随着儿童年龄的增长而逐渐成熟并自动化, 继而降低对数学能力的直接影响(Cantlon et al., 2009)。同时, 当儿童面临更加熟悉和自动化的数学任务时也将降低对于抑制控制能力的需求。如Yang等人(2019)的研究以5～6岁的中国香港儿童为被试, 对执行功能与数学技能之间的关系进行了为期一年的追踪, 发现抑制控制和计算、简单应用问题之间的联系从幼儿园的正相关变为一年级时不存在相关关系。这说明儿童从幼儿园过渡到一年级时出现了更加熟练化的基本数学技能(如, 计算), 使得执行功能在解决数学问题中的作用下降。而在本研究中, 研究对象为小学三～六年级的儿童, 此年龄段儿童的数学能力已经获得了一个较大的发展, 在进行数学任务时无需再调用大量的控制资源去抵制分心刺激和抑制与任务无关的反应, 因此, 抑制控制在完成数学任务中的作用将大大减小。

4.2 执行功能各成分与不同年级儿童数学能力间的关系

本研究从横向的视角考察了不同年级阶段儿童各执行功能成分在不同数学能力中的作用。研究结果表明, 除抑制控制外, 其余各执行功能成分对不同数学能力的预测作用将随儿童年级的增长而发生变化。从趋势上来看, 工作记忆广度是预测低年级阶段儿童三种数学能力的核心执行功能成分, 而工作记忆刷新和认知灵活性等高阶执行功能成分将在小学高年级儿童数学能力的发展中起重要作用。这说明年龄是影响各执行功能成分和儿童不同数学能力关系的重要因素。

基于横向研究的结果, 本研究发现工作记忆广度对三种数学能力的预测作用在高、低年级阶段呈现出不同的模式。具体而言, 相比于高年级阶段儿童, 工作记忆广度对低年级阶段儿童数学能力的预测作用更大。对于低年级儿童而言, 由于儿童数学技能的水平较低, 致使在加工这些数学任务时需要使用较大的工作记忆容量去存储与任务有关的背景信息, 同时还需要从长时记忆中检索数学事实和提取有利于解决问题的策略(Miller-Cotto & Byrnes, 2020)。因此, 工作记忆广度成为低年级儿童顺利解决数学问题的重要前提。然而, 对于高年级儿童来讲, 由于儿童对数学技能和数学策略的掌握更加熟悉与自动化, 在解决数学问题时趋向于使用事实检索和分解策略, 通过将问题划分为更小和更易解决的子步骤来使问题得以解决(Cragg et al., 2017), 从而降低了对工作记忆容量的需求(Bailey et al., 2012)。现有的相关研究也证实了这一观点, 如Chen和Bailey (2021)使用元分析的方法考察了工作记忆和计算能力之间的关系, 发现两者之间的联系将随儿童年龄的不同而发生变化。具体来讲, 低龄儿童在完成简单算术问题时往往速度更慢以及采用不成熟的策略, 而年龄较大的儿童则倾向于使用更为有效的解题策略, 并降低对于工作记忆容量的需求。此外, 本研究还发现工作记忆刷新是预测高年级阶段儿童空间想象能力的重要因素, 其预测作用超过了工作记忆广度。研究显示, 作为一种更为高阶的认知能力, 工作记忆刷新会在更加复杂和不熟悉的任务中发挥更大的作用(Clements et al., 2016)。高年级儿童由于其刷新能力的进一步发展, 在对几何问题的表征和解题策略的运用上更为清晰和灵活, 从而可以更为积极的更改关于问题的心理图示, 使问题得以解决。

与假设相一致, 本研究发现认知灵活性更能预测小学高年级儿童的数学能力。已有研究表明, 作为执行功能成分中更为高阶的认知能力, 认知灵活性在学前阶段快速发展, 并在10岁左右出现较大的成熟(Dick, 2014), 这致使高年级儿童利用这一复杂认知能力来解决数学问题成为可能。对于高年级儿童来说, 认知灵活性有助于儿童从不同的角度审视问题, 使儿童可以习得致使犯错的经验并选择替代策略来最优化的解决数学问题(Yang et al., 2019; Yeniad et al., 2013)。

本研究是对以往有关执行功能与数学能力关系研究的验证和补充。结果表明, 学龄儿童不同的执行功能成分与数学能力的不同方面存在联系差异, 并且这种联系会因儿童年级水平的不同而发生变化。本横断研究在一定程度上解答了前人研究中的争议, 同时深化和拓展了相应的理论。首先, 与以往研究相一致, 本研究显示不同执行功能成分影响不同的数学能力, 工作记忆(工作记忆广度和工作记忆刷新)是影响儿童数学能力的核心执行成分(Cragg et al., 2017; Spiegel et al., 2021; der Ven et al., 2012), 而抑制控制(干扰抑制和反应抑制)则与学龄儿童的数学能力无关(Ellefson et al., 2020; Wang et al., 2019)。其次, 研究结果显示, 工作记忆广度对三种数学能力的影响将随着儿童年级水平的增高而降低, 而工作记忆刷新和认知灵活性则在小学高年级儿童数学加工中发挥更大的作用。这部分支持了“淡出”假说(Stipek & Valentino, 2015), 即随着年龄的增长, 工作记忆广度和抑制控制对于个体的发展将变得不太重要。但本研究的结果进一步说明, 在考察执行功能和数学能力的关系时, 还应考虑不同执行功能成分发展的特异性, 如随着更高阶执行功能成分(认知灵活性)的逐渐成熟, 这些认知成分是否将取代更为基础的能力(抑制控制), 从而在解决数学任务的过程中起更大的作用。因此, 全面了解各执行功能成分与不同数学能力之间关系的发展模式, 可以更好的揭示两者之间的实质联系。

4.3 研究不足与展望

本研究使用了横断研究的方法, 对不同年级阶段儿童各执行功能成分与不同数学能力的关系进行了探讨, 进一步明晰了执行功能和数学能力随发展的深层次关系。但仍旧存在一些不足之处。首先, 本研究作为一项短期的横断调查, 所得出的结论在一定程度上回答了以往研究的争议并对相应的理论做出了拓展, 但仍旧无法证实执行功能和数学能力之间的因果关系, 未来还需要更多的追踪和实证研究来评估两者之间的因果关系和影响机制。其次, 本研究较少考虑到影响儿童执行功能和数学能力关系的因素, 如加工速度、非言语智力和家庭社会经济地位等(Georgiou et al., 2020; Yang et al., 2019), 未来还需研究者在控制这些额外变量的基础上进一步对两者间的关系进行考察。最后, 已有研究发现, 执行功能对数困儿童的数学能力会有更大影响(Cragg et al., 2017), 未来研究还需进一步探讨数困儿童执行功能和数学能力之间的关系是否也符合这一发展模式, 从而为数困儿童进行相应的执行功能训练做出指引。

5 结论

本文通过考察三～六年级儿童各执行功能成分与不同数学能力的关系, 发现工作记忆广度是儿童数学运算能力和空间想象能力的重要预测因素, 而工作记忆刷新则更能预测儿童的逻辑思维能力。同时, 各执行功能成分对不同数学能力的预测作用会在高、低年级阶段呈现出不同的影响模式。在低年级阶段, 工作记忆广度是预测儿童三种数学能力的核心执行功能成分; 在高年级阶段, 工作记忆广度的预测力下降, 而工作记忆刷新和认知灵活性对数学能力的影响逐渐提升。这一发现在一定程度上揭示了各执行功能成分与不同数学能力的联系可能存在差异, 并且这种关系会随着年级的增高而发生变化。

Ahmed, S. F., Tang, S., Waters, N. E., & Davis-Kean, P. (2019). Executive function and academic achievement: Longitudinal relations from early childhood to adolescence.(3), 446–458.

Archambeau, K., & Gevers, W. (2018). (How) are executive functions actually related to arithmetic abilities?., 337– 357.

Bailey, D. H., Littlefield, A., & Geary, D. C. (2012). The codevelopment of skill at and preference for use of retrieval-based processes for solving addition problems: Individual and sex differences from first to sixth grades.(1), 78–92.

Best, J. R., Miller, P. H., & Jones, L. L. (2009). Executive functions after age 5: Changes and correlates.(3), 180–200.

Blakey, E., Matthews, D., Cragg, L., Buck, J., Cameron, D., Higgins, B., ... Carroll, D. J. (2020). The role of executive functions in socioeconomic attainment gaps: Results from a randomized controlled trial.(5), 1594–1614.

Bryce, D., Whitebread, D., & Szűcs, D. (2015). The relationships among executive functions, metacognitive skills and educational achievement in 5 and 7 year-old children.(2), 181–198.

Bull, R., & Lee, K. (2014). Executive functioning and mathematics achievement.(1), 36–41.

Bull, R., & Scerif, G. (2001). Executive functioning as a predictor of children's mathematics ability: Inhibition, switching, and working memory.(3), 273–293.

Camerota, M., Willoughby, M. T., & Blair, C. B. (2020). Measurement models for studying child executive functioning: Questioning the status quo.(12), 2236–2245.

Cantin, R. H., Gnaedinger, E. K., Gallaway, K. C., Hesson-McInnis, M. S., & Hund, A. M. (2016). Executive functioning predicts reading, mathematics, and theory of mind during the elementary years., 66–78.

Cantlon, J. F., Libertus, M. E., Pinel, P., Dehaene, S., Brannon, E. M., & Pelphrey, K. A. (2009). The neural development of an abstract concept of number.(11), 2217–2229.

Chen, E. H., & Bailey, D. H. (2021). Dual-task studies of working memory and arithmetic performance: A meta-analysis.(2), 220–233.

Cirino, P. T., Ahmed, Y., Miciak, J., Taylor, W. P., Gerst, E. H., & Barnes, M. A. (2018). A framework for executive function in the late elementary years.(2), 176–189.

Clements, D. H., Sarama, J., & Germeroth, C. (2016). Learning executive function and early mathematics: Directions of causal relations., 79–90.

Cragg, L., & Gilmore, C. (2014). Skills underlying mathematics: The role of executive function in the development of mathematics proficiency.(2), 63–68.

Cragg, L., Keeble, S., Richardson, S., Roome, H. E., & Gilmore, C. (2017). Direct and indirect influences of executive functions on mathematics achievement., 12–26.

Cueli, M., Areces, D., García, T., Alves, R. A., & González- Castro, P. (2020). Attention, inhibitory control and early mathematical skills in preschool students.(2), 237–244.

Dekker, M. C., Ziermans, T. B., Spruijt, A. M., & Swaab, H. (2017). Cognitive, parent and teacher rating measures of executive functioning: Shared and unique influences on school achievement., 48.

Diamond, A. (2013). Executive functions., 135–168.

Dick, A. S. (2014). The development of cognitive flexibility beyond the preschool period: An investigation using a modified Flexible Item Selection Task., 13–34.

Du, W. P. (2013). The evolution of the connotation of mathematical competence in elementary school mathematics syllabus or curriculum standards., 43–45.

[杜文平. (2013). 小学数学教学大纲或课程标准中数学能力内涵的演变., 43–45.]

Duncan, R. J., McClelland, M. M., & Acock, A. C. (2017). Relations between executive function, behavioral regulation, and achievement: Moderation by family income., 21–30.

Ellefson, M. R., Zachariou, A., Ng, F. F-Y., Wang, Q., & Hughes, C. (2020). Do executive functions mediate the link between socioeconomic status and numeracy skills? A cross-site comparison of Hong Kong and the United Kingdom., 104734.

Espy, K. A., McDiarmid, M. M., Cwik, M. F., Stalets, M. M., Hamby, A., & Senn, T. E. (2004). The contribution of executive functions to emergent mathematic skills in preschool children.(1), 465–486.

Fisk, J. E., & Sharp, C. A. (2004). Age-related impairment in executive functioning: Updating, inhibition, shifting, and access.(7), 874–890.

Friso-den Bos, I., der Ven, S. H., Kroesbergen, E. H., & Luit, J. E. (2013). Working memory and mathematics in primary school children: A meta-analysis., 29–44.

Fung, W. K., Chung, K. K. H., & Lam, C. B. (2020). Mathematics, executive functioning, and visual–spatial skills in Chinese kindergarten children: Examining the bidirectionality., 1–10.

Geary, D. C. (2004). Mathematics and learning disabilities.(1), 4–15.

Georgiou, G. K., Wei, W., Inoue, T., Das, J. P., & Deng, C. (2020). Cultural influences on the relation between executive functions and academic achievement.(4), 991–1013.

Gilmore, C., Keeble, S., Richardson, S., & Cragg, L. (2015). The role of cognitive inhibition in different components of arithmetic., 771–782.

Halberda, J., Mazzocco, M. M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlate with maths achievement.(7213), 665–668.

Harvey, H. A., & Miller, G. E. (2017). Executive function skills, early mathematics, and vocabulary in head start preschool children.(3), 290–307.

Hilbert, S., Bruckmaier, G., Binder, K., Krauss, S., & Bühner, M. (2019). Prediction of elementary mathematics grades by cognitive abilities.(3), 665–683.

Himi, S. A., Bühner, M., & Hilbert, S. (2021). Advancing the understanding of the factor structure of executive functioning.(1), 16.

Holmes, J., Gathercole, S. E., & Dunning, D. L. (2009). Adaptive training leads to sustained enhancement of poor working memory in children.(4), F9–F15.

Holmes, J., Guy, J., Kievit, R. A., Bryant, A., Mareva, S., & Gathercole, S. E. (2021). Cognitive dimensions of learning in children with problems in attention, learning, and memory.(7), 1454–1480.

Jenks, K. M., van Lieshout, E. C., & de Moor, J. M. (2012). Cognitive correlates of mathematical achievement in children with cerebral palsy and typically developing children.(1), 120–135.

Jiang, R., Li, X., Xu, P., & Chen, Y. (2019). Inhibiting intuitive rules in a geometry comparison task: Do age level and math achievement matter?., 1–16.

Kahl, T., Grob, A., Segerer, R., & Möhring, W. (2021). Executive functions and visual-spatial skills predict mathematical achievement: Asymmetrical associations across age.(1), 36–46.

Lan, X., Legare, C. H., Ponitz, C. C., Li, S., & Morrison, F. J. (2011). Investigating the links between the subcomponents of executive function and academic achievement: A cross- cultural analysis of Chinese and American preschoolers.(3), 677–692.

Lee, K., Ng, S. F., & Bull, R. (2018). Learning and solving algebra word problems: The roles of relational skills, arithmetic, and executive functioning.(9), 1758–1772.

Lehto, J. E., Juujärvi, P., Kooistra, L., & Pulkkinen, L. (2003). Dimensions of executive functioning: Evidence from children.(1), 59–80.

Lin, C. D. (2011).(4th ed.). Beijing: China Light Industry Press.

[林崇德. (2011).(第4版). 北京: 中国轻工业出版社.]

Magalhães, S., Carneiro, L., Limpo, T., & Filipe, M. (2020). Executive functions predict literacy and mathematics achievements: The unique contribution of cognitive flexibility in grades 2, 4, and 6.(7), 934–952.

McKenna, R., Rushe, T., & Woodcock, K. A. (2017). Informing the structure of executive function in children: meta-analysis of functional neuroimaging data., 154.

Miller-Cotto, D., & Byrnes, J. P. (2020). What’s the best way to characterize the relationship between working memory and achievement?: An initial examination of competing theories.(5), 1074–1084.

Monette, S., Bigras, M., & Guay, M-C. (2011). The role of the executive functions in school achievement at the end of Grade 1.(2), 158–173.

Nguyen, T., & Duncan, G. J. (2019). Kindergarten components of executive function and third grade achievement: A national study., 49–61.

Passolunghi, M. C., Mammarella, I. C., & Altoè, G. (2008). Cognitive abilities as precursors of the early acquisition of mathematical skills during first through second grades.(3), 229–250.

Peng, P., Congying, S., Beilei, L., & Sha, T. (2012). Phonological storage and executive function deficits in children with mathematics difficulties.(4), 452–466.

Peng, P., Wang, C., &mkung, J. (2018). Understanding the cognition related to mathematics difficulties: A meta-analysis on the cognitive deficit profiles and the bottleneck theory.(3), 434–476.

Raghubar, K. P., Barnes, M. A., & Hecht, S. A. (2010). Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches.(2), 110–122.

Rutherford, T., Buschkuehl, M., Jaeggi, S. M., & Farkas, G. (2018). Links between achievement, executive functions, and self‐regulated learning.(6), 763–774.

Spiegel, J. A., Goodrich, J. M., Morris, B. M., Osborne, C. M., & Lonigan, C. J. (2021). Relations between executive functions and academic outcomes in elementary school children: A meta-analysis.(4), 329–351.

St Clair-Thompson, H. L., & Gathercole, S. E. (2006). Executive functions and achievements in school: Shifting, updating, inhibition, and working memory.(4), 745–759.

Stipek, D., & Valentino, R. A. (2015). Early childhood memory and attention as predictors of academic growth trajectories.(3), 771–788.

Sulik, M. J., & Obradović, J. (2018). Teachers’ rankings of children’s executive functions: Validating a methodology for school-based data collection., 136–154.

Swanson, H. L. (2011). Working memory, attention, and mathematical problem solving: A longitudinal study of elementary school children.(4), 821–837.

Toll, S. W., van der Ven, S. H., Kroesbergen, E. H., & Luit, J. E. (2011). Executive functions as predictors of math learning disabilities.(6), 521–532.

der Ven, S. H., Kroesbergen, E. H., Boom, J., & Leseman, P. P. (2012). The development of executive functions and early mathematics: A dynamic relationship.(1), 100–119.

Viterbori, P., Traverso, L., & Usai, M. C. (2017). The role of executive function in arithmetic problem-solving processes: A study of third graders.(5), 595–616.

Wang, C., Jaeggi, S. M., Yang, L., Zhang, T., He, X., Buschkuehl, M., & Zhang, Q. (2019). Narrowing the achievement gap in low-achieving children by targeted executive function training., 87–95.

Wang, X. F., Liu, X. N., Zhao. X., & Zhou, R. L. (2011). The developmental research on the updating ability of primary school children with mathematics learning disabilities.(2), 47–57.

[王晓芳, 刘潇楠, 赵鑫, 周仁来. (2011). 小学数学学习障碍儿童刷新能力的发展性研究.(2), 47–57.]

Wang, Y., & Zhou, X. (2019). Longitudinal relations between executive function and internalizing problems in grade school: The role of peer difficulty and academic performance.(10), 2147–2158.

Wen. P., Zhang. L., Li. H., Liu. L. X-J., & Zhang. X-Y. (2007). Model of executive functioning as predictor of children’s mathematical ability.(3), 13–18.

[文萍, 张莉, 李红, 刘莉湘君, 张雪怡. (2007). 儿童执行功能对数学能力的预测模型.(3), 13–18.]

Wu, H. R., & Li. L. (2005). Development of chinese rating scale of pupil’s mathematic abilities and study on its reliability and validity.(4), 473–475.

[吴汉荣, 李丽. (2005). 小学生数学能力测试量表的编制及信效度检验.(4), 473–475.]

Yang, X., Chung, K. K. H., & McBride, C. (2019). Longitudinal contributions of executive functioning and visual-spatial skills to mathematics learning in young Chinese children.(5), 678–704.

Yeniad, N., Malda, M., Mesman, J., IJzendoorn, M. H., & Pieper, S. (2013). Shifting ability predicts math and reading performance in children: A meta-analytical study., 1–9.

Yu, P., & Zuo, M. L. (1996). The development of mathematical ability and cognitive structure of elementary school students in grades 3 to 6., 30–36.

[于萍, 左梦兰. (1996). 三～六年级小学生数学能力及认知结构的发展., 30–36.]

Zhang, J., Cheung, S. K., Wu, C., & Meng, Y. (2018). Cognitive and affective correlates of Chinese children’s mathematical word problem solving., 2357.

Zhao, X., Chen, L., & Maes, J. H. (2018). Training and transfer effects of response inhibition training in children and adults.(1), e12511.

Zhao, X., Jia, L. N., & Zan, X. Y. (2016). Interference control training: Effect and mechanism.(6), 900–908.

[赵鑫, 贾丽娜, 昝香怡. (2016). 干扰控制的训练: 内容、效果与机制.(6), 900–908.]

Role of executive function in mathematical ability of children in different grades

ZHU Xiaoliang, ZHAO Xin

(Key Laboratory of Behavioral and Mental Health of Gansu province, Northwest Normal University, Lanzhou 730070, China)(School of Psychology, Northwest Normal University, Lanzhou 730070, China)

Mathematical ability is an important component of children'sacademic achievement and critical to individual development. Executive function, as an essential cognitive ability, is a core cognitive element that supports children’s mathematical processing. However, there have only been a few studies focusing on the effects of each component of executive function on different mathematical abilities (mathematical operation, spatial imagination, and logical thinking). Primary school is the key period during which children acquire basic mathematical ability. However, limited studies have examined the developmental relationships between the various components of executive function and the different mathematical abilities of children at different grade levels. Consequently, the purpose of this study was to examine the role of each component of executive function in the different mathematical abilities of children at different grade levels.

A total of 812 children in grades 3, 4, 5, and 6 completed tests covering mathematical operations, spatial imagination, and logical thinking to measure their basic mathematical ability. The Stroop task and the GO/NOGO task were used to measure interference inhibition and response inhibition. Children’s working memory span was assessed using forward and backward digit span tasks. Children’s working memory updating was investigated using simple and difficult digital updating tasks. Children’s cognitive flexibility was examined using digit shifting tasks. Finally, a correlation analysis and a structural equation model (SEM) were used to investigate the impact of each component of executive function on children’s mathematical abilities at different grade levels.

The results revealed that working memory was the most important factor affecting children’s mathematical skills, over inhibitory control and cognitive flexibility. Specifically, working memory span was the most statistically significant predictor of ability with respect to mathematical operations, while working memory updating was a stronger predictor of spatial imagination and logical thinking abilityfrom grade 3 to grade 6. In a further analysis of the data, we divided the four grades into two stages, with grades 3 and 4 set as the younger group and grades 5 and 6 set as the older group. The results showed working memory span to be the most important predictor of mathematical operation ability, spatial imagination ability, and logical thinking ability in the junior grades. In the older students, the predictive effect of working memory span on basic math ability dropped, and the effects of working memory updating and cognitive flexibility on basic math ability increased.

These results indicate that different components of executive function play various roles in different mathematical abilities in school-age children, and that this pattern of influence appears to change as children progress through the grades. Specifically, the lower-order components of executive function components, specifically working memory span, were found to play an important role in the development of three mathematical abilities in younger students, while the higher-order executive function components, specifically working memory updating and cognitive flexibility, were found to play a more important role in processing mathematical tasks in older students.

executive function, mathematical abilities, primary school student, structural equation modeling

B844

2022-06-08

*国家自然科学基金项目(32260207), 教育部人文社会科学研究项目(21XJA190005), 西北师范大学研究生科研资助项目(2021KYZZ02031)资助。

赵鑫, E-mail: psyzhaoxin@nwnu.edu.cn