简化软信息迭代的遥测TPC译码算法

沈俞园,孙发鱼,2,艾冬生

(1.西安机电信息技术研究所,陕西 西安 710065;2.机电动态控制重点实验室,陕西 西安 710065)

0 引言

随着兵器靶场弹箭试验任务复杂程度的提高,对遥测系统的数据传输速率、通信距离和频带利用率提出了更高的要求。在高码速率和远距离无线遥测传输中,大气和地面等环境会对遥测信号产生干扰和多径等影响,因此需要对遥测发射的数字信号进行差错控制。信道编码是对数字信号进行差错控制的有效方法,可以提高传输质量,降低数据传输误码率。常用的信道编码包括TPC编码、RS编码、卷积编码、Turbo码等[1]。TPC编码是一种逼近香农极限的差错控制编码技术,比RS编码、卷积编码的编码增益更高,与Turbo码相比,编码增益不会随着码速率的提升而迅速下降。TPC编译码使用简便,码长灵活,不仅能够纠正由随机信道引起的错误,而且能够纠正由突发信道引起的错误,可适用于弹箭高码速率遥测数据的传输。

Chase2算法是一种TPC译码中使用较广泛的算法,但在实时性要求高的遥测系统中,存在译码过程繁琐、处理延时较大等问题。如何在译码性能与复杂度这两者间找到最佳平衡点是必须要解决的实际问题,对原始算法的改进势在必行[2]。

本文在探究TPC Chase2迭代译码算法的基础上,提出了软信息迭代简化算法,可以减少迭代译码次数,减少FPGA实现时的资源消耗。

1 TPC编译码原理

1.1 TPC编码方式

TPC码是一种将线性分组码进行串行级联,达到长码纠错的编码方式。常用子码类型有(扩展)汉明码、BCH码等。下面讨论最为常用的二维TPC码编码过程。

编码过程如图1所示。图1中,将待编码信息组成k2×k1的矩阵;用分组码C1(n1,k1),对各行进行编码;用分组码C2(n2,k2),对各列进行编码;结果得到二维n2×n1的数据矩阵,其中右下角为校验位的校验,且先行后列的编码方式与先列后行的编码方式是等效的。实际应用中,大多优先选择C1与C2相同的分组码。

图1 TPC编码过程Fig.1 TPC encoding process

1.2 TPC译码方式

TPC 译码主要包括硬判决和软判决两种。硬判决译码是利用解调器判决输出的单比特信息1或0进行译码的过程,而软判决译码则能利用传输信道产生的软信息进行译码。

TPC 软判决译码算法通常比硬判决译码有更好的差错控制表现。研究表明,采用软判决的似然译码比硬判决译码高出2～3 dB的编码增益。软判决译码的优势是充分利用了解调软信息,并因此获得了较高的增益和较低的误码率[3]。

软判决译码通常是SISO译码,有别于硬判决译码的单比特信息码字输入,软判决译码的输入信息是解调后的多个比特表示的数值,习惯上称其为软信息。如图2(a)所示,解调输出的多比特信息经硬判决处理后转为单比特数据,再送入硬判决译码模块中;图2(b)给出了软判决译码的输入示意图,解调模块输出的软信息直接送入到软判决译码模块中。软判决译码充分利用了前级解调模块输出的软信息,因此避免了多比特数据判决成单比特数据所造成的信息损失,相对于硬判决译码而言具有更好的译码性能。

1.3 Chase2译码算法

TPC 译码原理主要使用软判决译码,在软判决译码算法中Chase2算法是一种很经典的算法。该算法是一种针对线性分组码的软入硬出译码算法,译出的码字为硬输出。

图2 硬判决与软判决输入示意图Fig.2 Schematic diagram of hard decision and soft decision input

Chase2 算法的译码性能接近最大似然译码,是一种次优译码算法,复杂度比较低,可以使得译码的误码率降到很低。Chase 算法分为 Chase1、Chase2 和 Chase3 三类算法,它们的主要区别是测试序列产生的方式不同。Chase2是 Chase1 和 Chase3 算法的折中,它的译码复杂度和译码性能介于 Chase1和 Chase3之间,适用范围也比较广泛[4]。因此实际应用中,我们针对 Chase2软判决译码进行改进。

Chase2算法的工作原理:将未同步输出的软信息(判决前的信息)向量作为TPC解码输入,根据信息幅值,选取最不可靠的n位,形成错误样本集合;从错误样本集合中找出与接收向量欧式距离最小的子码为候选子码,同时利用外信息向量记录各位的软判决可靠度,进行迭代,经过多轮次迭代后完成解码。Chase2译码算法实现步骤如图3所示。

图3 Chase2译码算法步骤Fig.3 Chase2 decoding algorithm steps

1) 对接收序列R(即软信息)进行硬件判决(当软信息大于0时,令其对应试探序列为1,否则为0),得到码字Y。

2) 确定可靠性最低的p个码元(计算接收信息的绝对值|rj|即可,|rj|的绝对值越大可信度越高);

计算R与Y的欧氏距离,得到Y中p个可靠性最差的码元,并产生q=2p个测试图样Tq,p=2时错误图样如图4所示,其中A、B即为选出的低可靠度码元。

3) 产生测试序列Zi=xor(Y,Ti)。

4) 确定候选码字集合

对序列Zq采用硬判决译码方式进行处理,所得结果形成一个集合,叫做候选码字集合,可用Ω表示。

5) 寻找似然码字

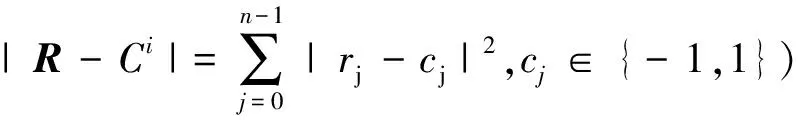
6) 计算软输出信息和外信息

译码得到r′j,必须要找到两个码字C+1(j)和C-1(j),似然码字D必是其中之一,需要找到另一个码字。具体方法是,在Ω中寻找与D第j位不同的候选码字搜索完成后,比较这些码字与R间的欧氏距离,此时距离最近的码字被称作竞争码字,记为C。

TPC译码就是将上述译码过程,经过多次行译码迭代和列译码迭代,最终得到译码结果[4]。

图4 错误图样p=2Fig.4 Error pattern p=2

传统的Chase2软判决译码算法是一种软输入硬输出(SIHO)算法,纠错能力不能得到保证[5]。为了提高TPC译码性能,需要采用迭代方法。自TPC码提出后,一直采用迭代译码的方法。

由此,可考虑对软信息更新方式的简化。

2 简化软信息迭代译码算法

由式(1)和式(2)分析可知,软信息的更新会极大地占用硬件空间,不利于硬件的实现。另外,原Chase2算法迭代方式确实会使精度增加,但是同时会极大地增加译码复杂度[6]。本文对软信息更新方式及译码迭代次数两个方面进行Chase2算法的简化,达到降低算法复杂度及硬件实现的目的。

2.1 简化软信息更新方式

软判决译码时需要从信道获得软信息,一般通过解调同步等步骤后产生软判决译码的输入信息。译码过程中,软信息的更新方式为

R(m)=R+α(m)·W(m),

(3)

式(3)中,m为行/列译码时数据序列的编号,R是TPC译码器接收到的原始信息比特,R(m)是输入行/列译码器的软信息,α(m)是基于经验值的缩放因子,W(m)是外信息矩阵。下一次输入行/列译码器的软信息,可由上一次软信息与外信息矩阵元素相加来获得。

需要指出的是,由于在历次迭代时,均需要使用R矩阵,故其需要从译码开始保存至译码结束[7-8]。在FPGA实现时,需要开辟一个固定的RAM空间,大小为n2×n1×L(L为量化位宽)。同时,每次更新得到的R(m)也需要存储,大小亦为n2×n1×L[9]。

考虑到随着迭代次数的增加,R(m)逐渐收敛到正确的软信息矩阵,可以用一次迭代生成的软信息矩阵R(m-1)替代R矩阵,进行软件信息更新。

由此,软信息的更新方式可改写为

R(m)=R(m-1)+α(m)·W(m),且有R(0)=R。

(4)

在硬件实现时,R(m)与R(m-1)可以共用同一块RAM,节省的RAM资源为n2×n1×L比特[10]。

2.2 简化译码迭代次数

在对k2行进行译码时,对k2×k1信息位进行纠错;在k1列进行译码时,k2×k1信息位进行二次纠错,保证了信息位的纠错能力。对(n2-k2)行和(n1-k1)列进行译码,是对校验位进行纠错,进一步提升了纠错能力。

因此,在信噪比较高的情况下,可以省略(n2-k2)行和(n1-k1)列的译码,只进行前k2和k1列的译码。由此,每次完整迭代需要进行的译码由(n2+n1)减少至(k2+k1),则译码完成减少的总迭代次数为(n2+n1-k2-k1)×N,其中N为TPC译码需要的总的迭代次数[11]。

结合上述对于TPC译码Chase2译码算法的简化方法,提出一种同时采用减少译码迭代次数和优化软信息更新方式的简化Chase2译码算法。

2.3 软信息迭代简化法

对原算法进行软信息更新方式与迭代次数的双重简化,公式R(m)=R+α(m)·W(m)可变为R(m)=R(m-1)+α(m)·W(m),且有R(0)=R;另外,省略行校验列与列校验行的译码,只进行k2和k1的译码,译码完成减少的总迭代次数为(n2+n1-k2-k1)×N。

软信息迭代简化法弥补了原算法步骤复杂、硬件复杂度高的问题,虽然会使软信息矩阵精度变差,但是可以使迭代次数减少,减少译码算法运算量、降低存储要求 ,即只付出了一点代价就可以极大地提高译码性能。

3 仿真验证

3.1 算法复杂度分析

表1列出了未经改进的原算法、简化软信息更新法、简化迭代次数法及软信息迭代简化法各自减少的迭代次数。简化软信息更新法用一次迭代生成的软信息矩阵R(m-1)替代R矩阵,进行软件信息更新,所减少的迭代次数为N-1;简化迭代次数法减少了行校验与列校验的重复迭代,从而减少了(n2+n1-k2-k1)×N次迭代;软信息迭代简化法迭代次数减少了(n2+n1-k2-k1)×N+N-1次。与简化软信息更新法相比,软信息迭代简化法更容易硬件实现,与简化迭代次数法相比,降低算法复杂度的同时,误码率降低,提高了译码性能。

表1 四种算法复杂度比较Tab.1 Four algorithms complexity comparison

3.2 误码率仿真分析

本文在高斯白噪声条件下,对QPSK调制和二维TPC译码器进行仿真,分量码选择为(64,57)的扩展汉明码,简记为TPC(64,57)×(64,57)。仿真涉及到的具体参数有:缩放因子α=[0, 0.2, 0.3, 0.5, 0.7,0.9,1,1];可靠因子β=[0.2, 0.4, 0.6, 0.8,1, 1,1,1];不可靠码元个数p=4;完整译码迭代次数N=4(行列各进行4次迭代译码);信息位个数为2×107;信噪比Eb/N0取值范围为2～6 dB,步进0.2 dB。

算法性能对比如图5所示,no FEC曲线为不使用信道编码时QPSK的误码率曲线,TPC曲线为原始TPC译码算法的误码率曲线,TPC_Modified1是简化软信息更新方式后译码算法的误码率曲线,TPC_Modified1是简化译码次数后的译码算法误码率曲线,TPC_Modified_both是同时使用两种简化方法后的译码算法误码率曲线。

图5 Chase算法以及简化算法性能对比图Fig.5 Performance comparison chart of Chase algorithm and simplified algorithm

由图5可知,使用TPC编译码后,在误码率10-5处,有5.5 dB左右的编码增益。相较于Chase2算法,TPC_Modified1约有0.2 dB的性能损失,TPC_Modified2约有0.4 dB的性能损失,TPC_Modified_both约有0.6 dB的性能损失。各改进算法的性能损失,分别相当于原始算法编码增益的3.6%、7.3%和10.9%。因此,从数据上看,简化算法对译码性能影响不大。

从仿真结果上看,简化软信息更新方式的影响更小,这是因为,随着迭代次数的增加,软信息矩阵逐渐收敛,更加趋近于真实值,与接收到的原始信息矩阵也更为接近。而改进次数的算法中,每次迭代省略了2·(N-K)(此处为2·(64-57)=14)次迭代,且没有利用信息矩阵右下角部分(校验位的校验),因此性能损失更大。当同时利用两种简化算法时,软信息矩阵精度变差,同时迭代次数减少,导致性能损失最大。

由此,本文改进算法在减少译码算法运算量、降低存储要求的同时,性能损失小于1 dB。因此,两种改进算法均实现了译码性能与运算量、资源消耗量的折中平衡,降低了硬件实现的复杂度。本文改进算法复杂度更低,而译码性能只是略有下降。

4 结论

本文针对TPC译码中经典的Chase2算法,结合了软信息更新与译码迭代次数的改进办法,提出一种软信息迭代简化法。仿真结果表明,软信息迭代简化法可以在适度降低译码性能的条件下,降低译码算法的复杂度、运算量和硬件资源消耗。