基于刚体外弹道学仿真的中大口径旋转炮弹引信力学环境

彭启蒙,王雨时,项 帆,闻 泉,王光宇

(南京理工大学机械工程学院,江苏 南京 210094)

0 引言

引信多数位于弹头,少数位于弹尾,个别位于弹身,因而绝大多数引信远离弹丸质心。弹丸的绕质心运动对引信及其零部件影响很大。引信的精细设计特别是预防弹道炸,要求精准研究弹丸外弹道上的绕质心运动,用常用的欧拉角系统来描述,就是章动、进动和自转。

尽管近年来伴随着引信计转数定距技术的发展,已有一些弹丸外弹道自转角速度衰减规律研究,并取得了较大的进展[1-3],但仍有必要探讨通过弹丸刚体外弹道模型求解的方法得出外弹道自转角速度衰减规律。目前外弹道起始段的章动规律是采用测试方法得到的,试验误差和数据处理方式不当都有可能导致所得章动规律有误[4-6]。另外,也未见有文献披露弹丸全弹道的章动运动规律。

为准确预知中大口径旋转弹丸在外弹道上的运动规律特别是章动规律,以美军155 mm口径火炮M107榴弹和俄军76 mm口径舰炮榴弹为例,用刚体外弹道模型对旋转弹丸外弹道阶段的运动进行仿真,即利用Matlab软件解算弹丸六自由度外弹道微分方程组,得出中大口径火炮旋转弹丸外弹道上极端爬行过载、章动规律、进动规律和转速衰减规律,供旋转炮弹引信及其零部件在外弹道上力学环境分析参考。

1 弹丸刚体外弹道仿真

弹丸刚体外弹道模型的建立同参考文献[7],弹丸章动、进动规律的计算公式同参考文献[8]。解算弹丸六自由度外弹道微分方程组需要一定的初始条件,即弹丸结构特征数、气动力参数、发射初始条件和气象条件。

1.1 弹丸刚体外弹道仿真初始条件

解算弹丸六自由度刚体外弹道模型的气象条件包括气温t0N、空气密度ρ0N、气压p0N、地面虚温τ0N、声速cs0N,忽略风的影响。气象条件的数值如表1所示。

表1 解算弹丸刚体外弹道模型的气象条件数值Tab.1 Numerical values of meteorological conditions for solving the rigid external ballistic model of the projectile

M107榴弹与76 mm口径舰炮榴弹的结构特征数与初始发射条件分别如表2和表3所示。解算弹丸六自由度刚体外弹道模型时,忽略弹丸径向偏心和动不平衡角,即将弹丸的偏心距和动不平衡角设为0。

表2 76 mm口径舰炮榴弹与M107榴弹外弹道仿真结构特征数Tab.2 The number of structural features of the 76 mm caliber grenade andthe M107 grenade’s external ballistic simulation

表3 76 mm口径舰炮榴弹与M107榴弹外弹道仿真发射初始条件Tab.3 The initial conditions of the 76 mm caliber grenade andthe M107 grenade’s external ballistic simulation launch

弹丸在运动过程中,由于受到各种干扰,弹丸轴线与质心速度方向不能保持一致,因此形成了攻角,对于高速旋转弹,又称为章动角。由于攻角的存在,又会产生与之相应的空气动力和力矩[7]。弹丸的空气动力和力矩参数可通过Fluent软件仿真得到,文献[10]将通过商业软件Fluent仿真得到的3°攻角下155 mm口径弹丸空气动力和力矩系数与试验值进行对比,误差在10%以内,表明Fluent软件仿真结果的可信性。由于文献[10]所用的155 mm榴弹外形结构与M107榴弹大致相同,所以用同样方法仿真得到的M107榴弹的气动力参数是可信的。

应用Fluent软件,仿真得3°攻角时M107榴弹与76 mm口径舰炮榴弹弹丸的阻力系数、升力系数、马格努斯力系数、马格努斯力矩系数、翻转力矩系数和极阻尼力矩系数,分别如表4和表5所列。

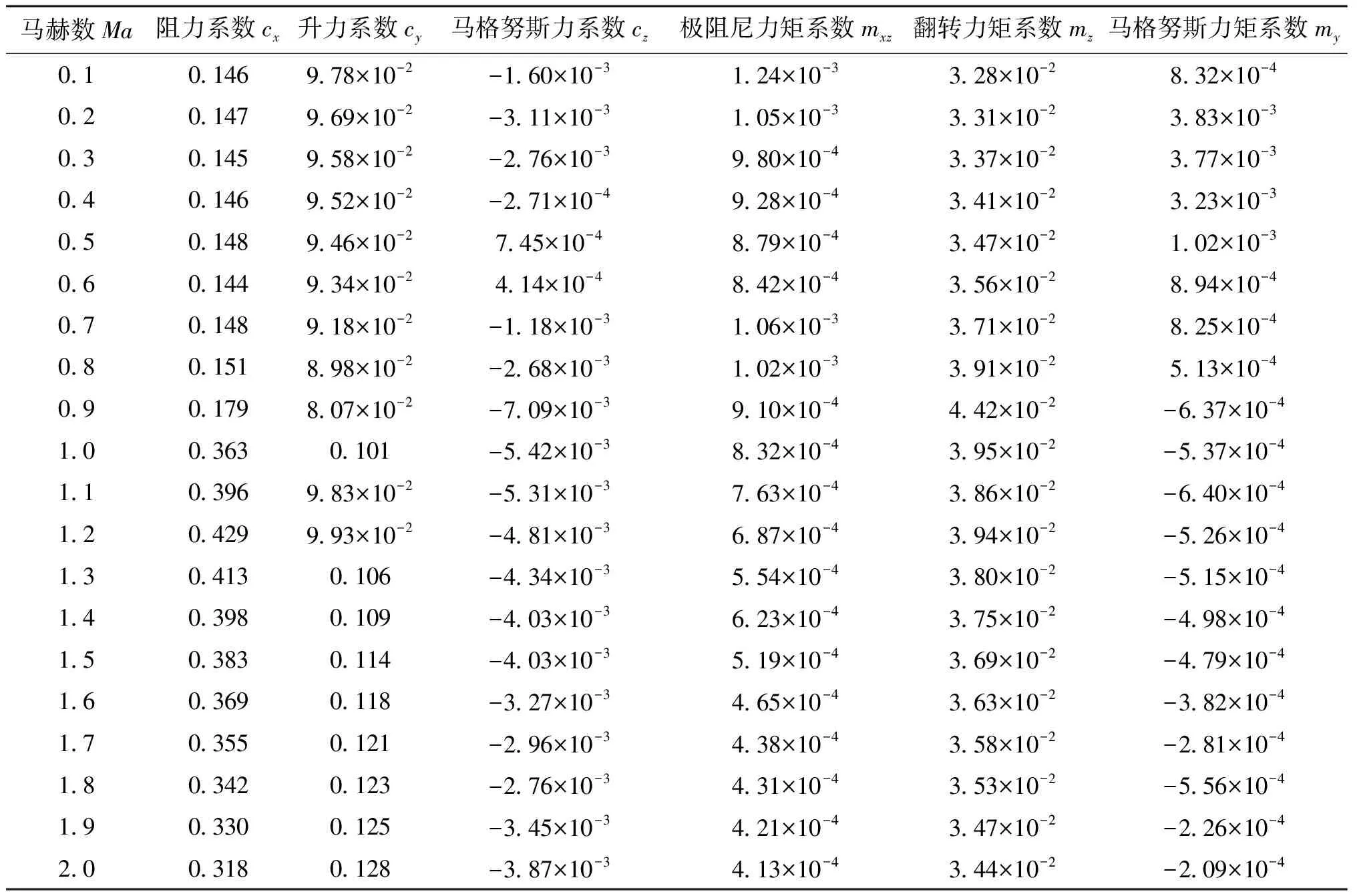
表4 3°攻角条件下Fluent仿真得到的155 mm加榴炮M107榴弹弹丸空气动力和力矩系数Tab.4 Aerodynamic and moment coefficients of the M107 grenade projectileobtained by Fluent simulation under the condition of 3° angle of attack

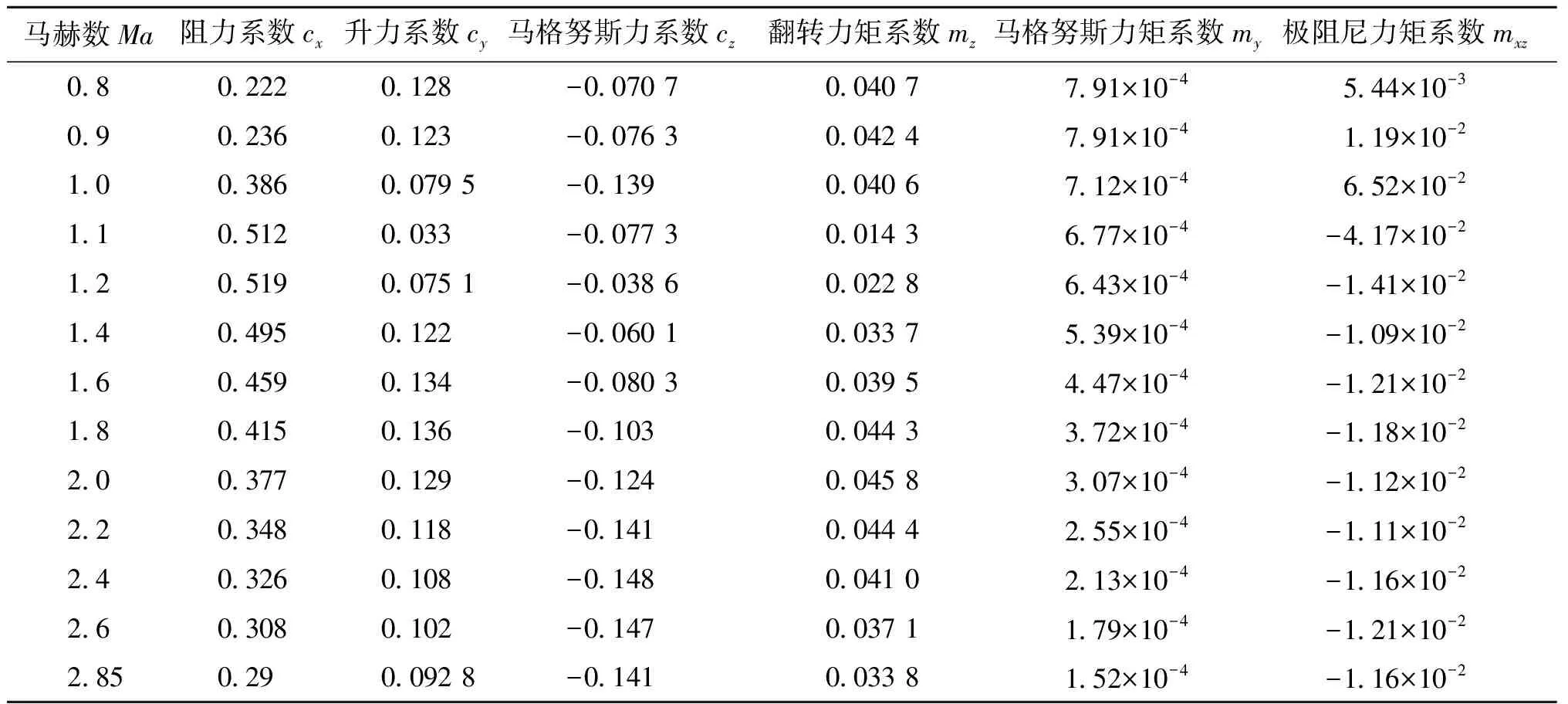
表5 3°攻角条件下Fluent仿真得到的76 mm口径舰炮榴弹弹丸空气动力和力矩系数Tab.5 Aerodynamic and moment coefficients of 76 mm caliber grenade projectilesobtained by Fluent simulation under the condition of 3° angle of attack

应用Fluent软件分别仿真76 mm口径舰炮榴弹与155 mm加榴炮M107榴弹在1°、2°、3°和4°攻角下的空气动力系数和空气动力力矩系数。利用Matlab软件中的四阶龙格-库塔法解算六自由度外弹道微分方程组,采用二维插值函数interp2和三次样条插值函数spline对马赫数和攻角插值,从而获取弹丸在整个飞行过程中连续的空气动力系数和空气动力力矩系数。

1.2 155 mm口径火炮M107榴弹刚体外弹道仿真

通过弹丸刚体外弹道模型与质点弹道方程解算不同射角下M107榴弹弹丸弹道曲线和速度随时间变化曲线分别如图1和图2所示。表6为45°射角下弹丸刚体外弹道模型与质点弹道方程解算M107榴弹弹丸外弹道飞行参数。

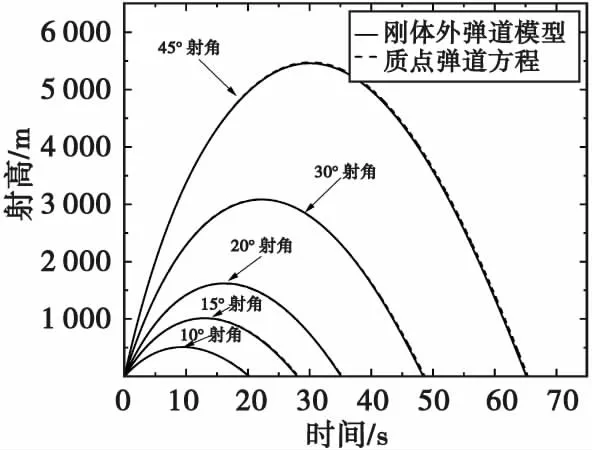
图1 解算不同射角下刚体外弹道模型与质点外弹道模型得到的M107榴弹飞行高度随时间变化曲线Fig.1 The time-varying curves of the flight height of the M107 grenade obtained by solving the rigid external ballistic model and the particle external ballistic model under different firing angles

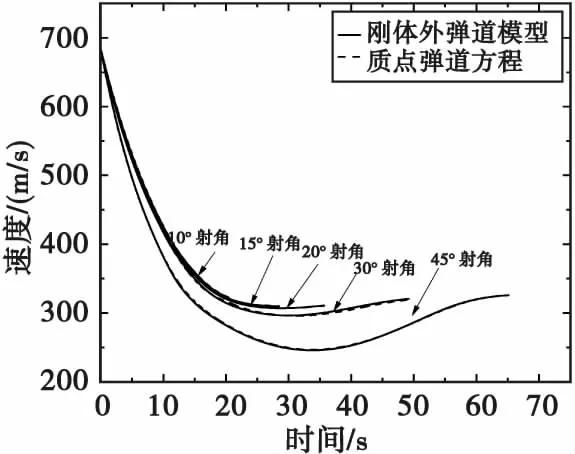
图2 解算不同射角下刚体外弹道模型与质点外弹道模型得到的M107榴弹速度随时间变化曲线Fig.2 The curves of M107 grenade velocity versus time obtained by solving the rigid external ballistic model and particle external ballistic model under different firing angles

由表6可知,弹丸刚体外弹道模型解算结果与质点外弹道模型解算结果相差最大不超过1%,且两种模型得到的弹丸飞行速度规律以及弹道曲线相似,说明弹丸刚体外弹道模型解算结果较为可信。相比于质点外弹道模型,刚体外弹道模型还能解算出弹丸的转速变化规律与偏流。

1.3 76 mm口径舰炮榴弹刚体外弹道仿真

通过弹丸刚体外弹道模型解算得到的76 mm口径舰炮榴弹弹道曲线和速度随时间变化曲线如图3所示。表7为21.5°射角下76 mm榴弹落地转速实测值与仿真值,图4为通过刚体外弹道模型、转速衰减模型、柔格里经验公式、幂函数经验公式和指数函数经验公式得到的不同射角下的76 mm口径舰炮榴弹的转速衰减规律对比。

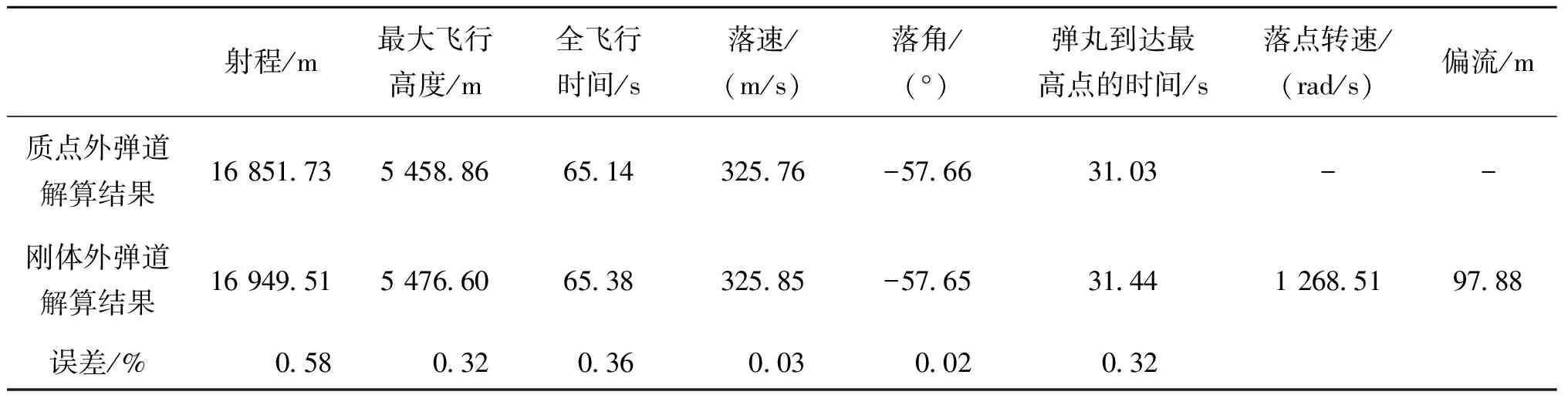
表6 45°射角下155 mm口径火炮M107榴弹弹丸刚体外弹道模型解算结果与质点外弹道解算结果对比Tab.6 Comparison of the calculation results of the rigid external trajectory of the 155 mm caliber artillery M107 grenade projectile and the calculation results of the particle external trajectory at a shooting angle of 45°

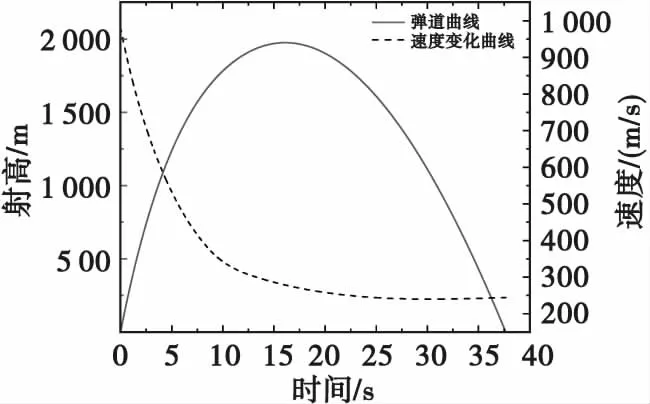
图3 刚体外弹道模型解算得21.5°射角下76 mm口径舰炮榴弹弹道曲线与速度变化曲线Fig.3 The ballistic curve and velocity change curve of the 76 mm caliber naval gun howitzer at a firing angle of 21.5° obtained from the solution of the rigid external ballistic model

表7 21.5°射角下76 mm口径舰炮榴弹落点转速实测值与仿真值对比Tab.7 Comparison of the measured and simulated values of the rotational speed of the 76 mm caliber grenade at the shooting angle of 21.5°

由图4和表7可见,由刚体外弹道模型得到的转速衰减曲线与由幂函数经验公式得到的曲线基本一致,而由修正后的柔格里经验公式和由指数函数经验公式得到的转速衰减曲线结果偏大。由刚体外弹道模型解算出的弹丸落点转速比实测值偏大,原因可能是在对弹丸进行Fluent气动特性仿真建模时,对弹带被火炮阳线切槽和弹头引信上的扳手孔等特征进行了简化,所得极阻尼力矩系数系统偏小。

表8列出了21.5°射角下76 mm口径舰炮弹丸刚体外弹道模型解算结果与质点外弹道模型解算结果,两相比较,最大误差1.19%,说明刚体外弹道模型解算过程和结果可信。

2 引信外弹道力学环境

弹丸刚体外弹道模型,在第1章用于155 mm和76 mm口径榴弹的外弹道仿真,已经证明其结果是可信的。本章以此为基础,进一步研究155 mm和76 mm口径榴弹引信外弹道上的爬行过载环境、章动环境、自转环境和进动环境,其结果也应该是可信的。

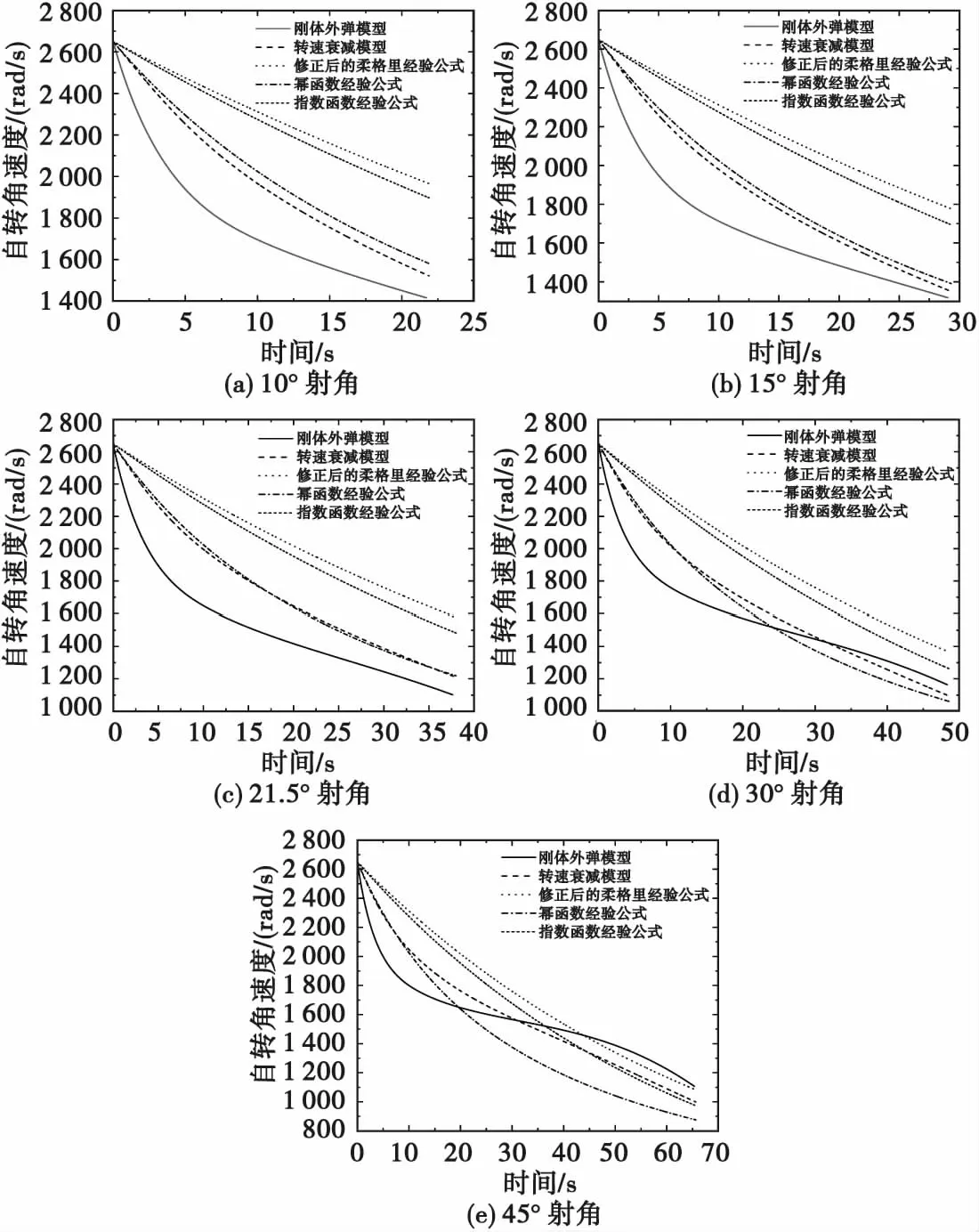
图4 不同射角下各方法得到的76 mm弹丸转速变化曲线Fig.4 Curves of the rotational speed of the 76 mm projectile obtained by each methodunder different shooting angles

2.1 爬行过载

弹丸在飞过后效期后,所受的轴向惯性力可分为爬行力和章动力。弹丸所受的爬行过载对弹丸弹道炸可能会有影响。

求解弹丸刚体外弹道模型得21.5°射角下76 mm口径舰炮榴弹和在45°射角下M107榴弹爬行过载分别是14.56g和4.87g,而质点外弹道模型求得的过载分别是13.51g和4.69g,两者分别相差7.21%和3.70%,比较接近。

2.2 章动规律

由弹丸刚体外弹道模型分别求得76 mm口径舰炮榴弹在射角为21.5°、初始章动角为3°和M107榴弹在射角为45°、初始章动角为3°时的章动角变化规律,如图5所示。

以M107榴弹为研究对象,分析其在初始章动角为3°时不同射角下章动角变化情况,如图6所示。

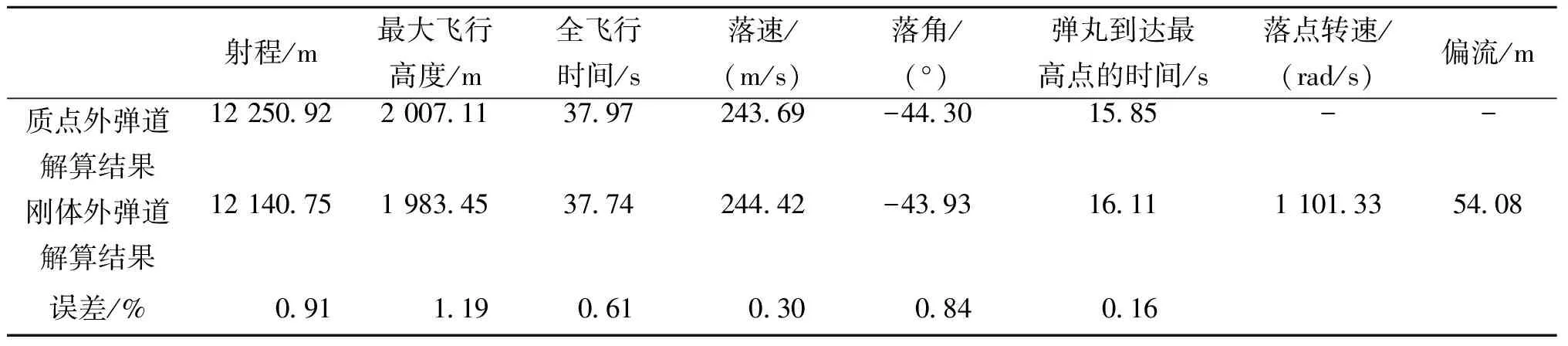
表8 21.5°射角下76 mm口径舰炮弹丸刚体外弹道模型解算结果与质点外弹道模型解算结果对比Tab.8 Comparison of the solution results of the 76 mm caliber grenade rigid external ballistic model and the particle external ballistic model at a shooting angle of 21.5°

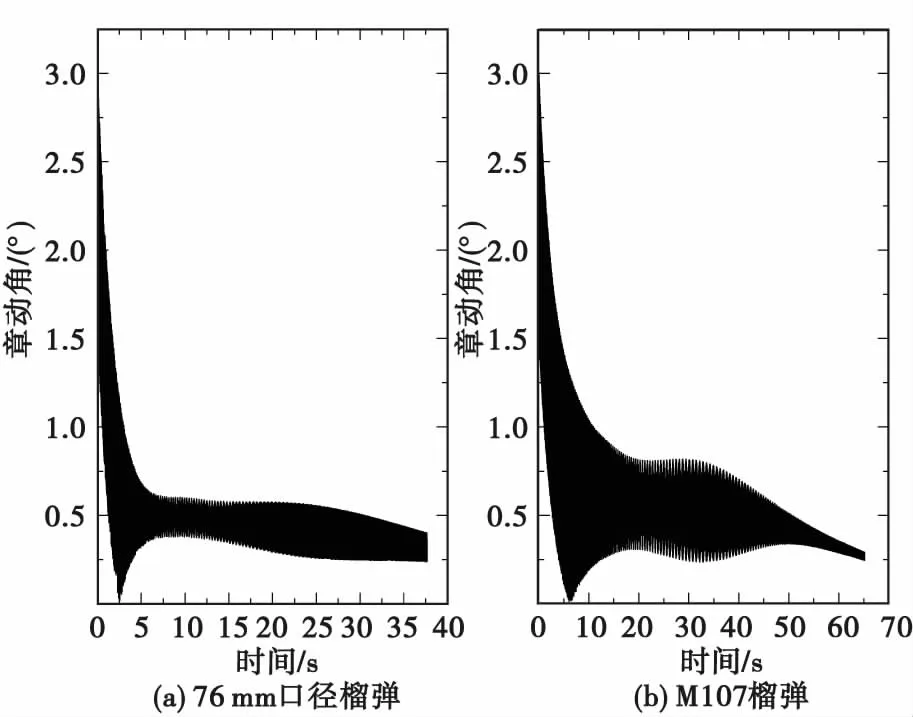
图5 弹丸章动角随时间的变化规律Fig.5 Variation of projectile nutation angle with time

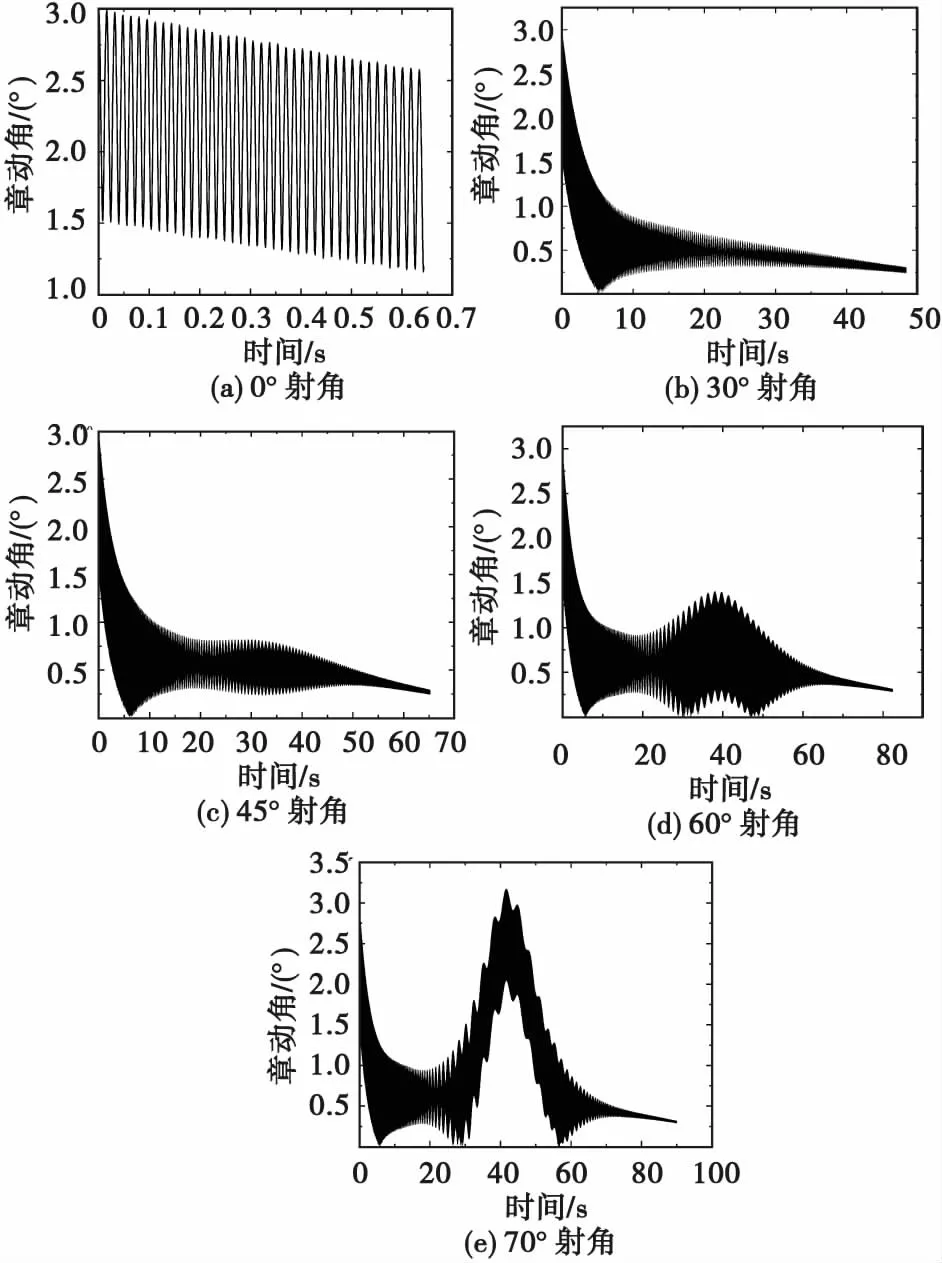
图6 不同射角下M107榴弹章动角随时间变化规律Fig.6 Variation of the nutation angle of the M107 grenade with time under different shooting angles

与图6类似,76 mm口径舰炮榴弹在初始章动角为3°时不同射角下章动角随时间变化曲线如图7所示。

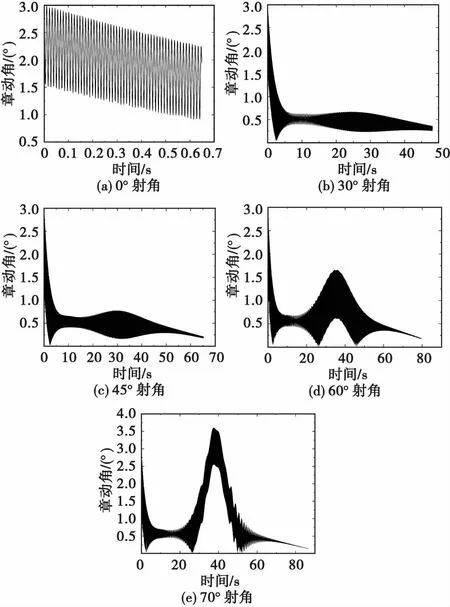
图7 不同射角下76 mm口径榴弹章动角随时间变化规律Fig.7 Variation of nutation angle of 76 mm caliber grenade with time under different firing angles

从图5可看出章动角变化规律是一条震荡曲线,在出炮口时刻最大,随后不断减小,直到趋于稳定。从图6和图7可看出:弹丸以45°以下射角射击时,最大章动角在全弹道上逐渐衰减;而以45°以上射角射击时,最大章动角总体上也是在全弹道上逐渐衰减,但在弹道顶点附近会略有增大。未见有文献给出的结果或结论与本节结果或结论相悖。

2.3 转速衰减规律

对于旋转弹而言,受极阻尼力矩影响,出炮口后转速在不断衰减,由刚体外弹道模型解算出的不同射角下76 mm口径舰炮榴弹和M107榴弹的自转角速度曲线分别如图8和图9所示。

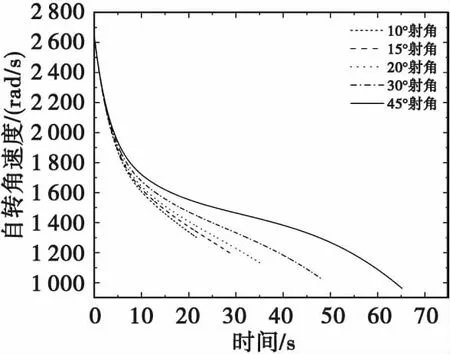
图8 不同射角下76 mm口径舰炮榴弹自转角速度变化曲线Fig.8 Variation curves of rotation angular velocity of 76 mm caliber grenades under different shooting angles

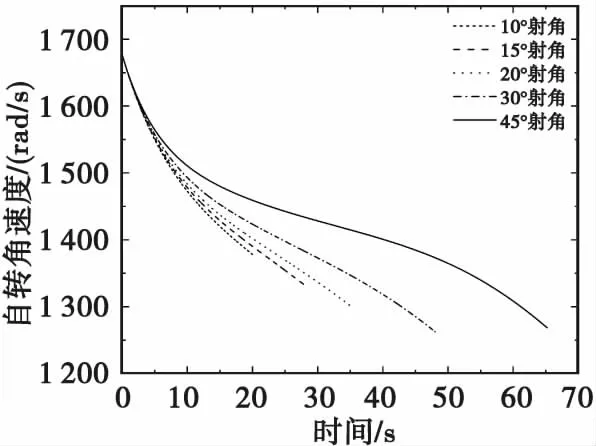
图9 不同射角下M107榴弹自转角速度变化曲线Fig.9 Variation curves of M107 grenade rotation angular velocity under different shooting angles

从图8和图9可看出,弹丸自转角速度大小在飞行期间持续衰减,且随着射角增大,自转角速度衰减有所减慢。

2.4 进动规律

式中,A为弹丸极转动惯量,C为赤道转动惯量,ω0为弹丸炮口转速。

用传统绕心运动方程求解弹丸进动规律,只适用于弹丸外弹道初始段。传统绕心运动方程假设在弹丸外弹道初始段,弹道呈直线,弹道倾角变化不明显,只考虑翻转力矩对弹丸的作用,弹丸速度和转速不衰减。

基于弹丸刚体外弹道模型求解76 mm口径榴弹在射角为0°、初始章动角为3°和M107榴弹在射角为0°、初始章动角为3°时外弹道得进动角速度变化规律,如图10和图11所示。

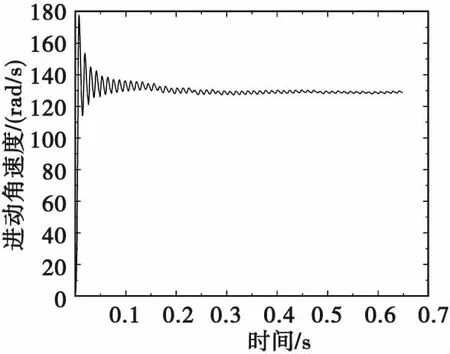
图10 76 mm口径榴弹在0°射角下进动角速度变化规律Fig.10 Variation law of precession angular velocity of 76 mm caliber grenade at 0° firing angle

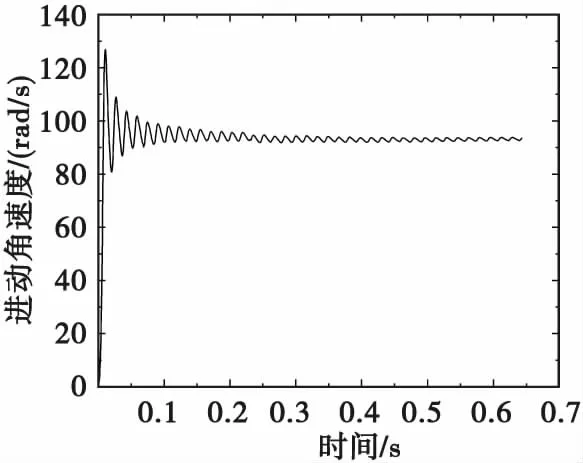
图11 M107榴弹在0°射角下进动角速度变化规律Fig.11 Variation law of precession angular velocity of M107 grenade at 0° shooting angle

从图10和图11可看出,以0°射角射击时,76 mm口径榴弹和M107榴弹的进动角速度在炮口附近波动均较大,随后分别逐渐稳定于130 rad/s和93 rad/s。通过传统绕心运动方程计算得到的76 mm口径榴弹和M107榴弹外弹道初始阶段进动角速度分别为142.7 rad/s和99 rad/s。应用刚体外弹道模型求解弹丸外弹道进动角变化规律时,在弹丸外弹道初始阶段,章动角变化呈简谐曲线且衰减不大,弹丸速度和转速衰减较小,与传统绕心运动方程假设吻合。将传统绕心运动方程求解结果与刚体外弹道模型求解结果对比,相对误差分别为8.90%和6.06%,表明应用刚体外弹道模型解算弹丸进动角速度可信。

以M107榴弹和76 mm口径榴弹为研究对象,分析不同射角下弹丸的进动角速度变化规律,如图12所示。

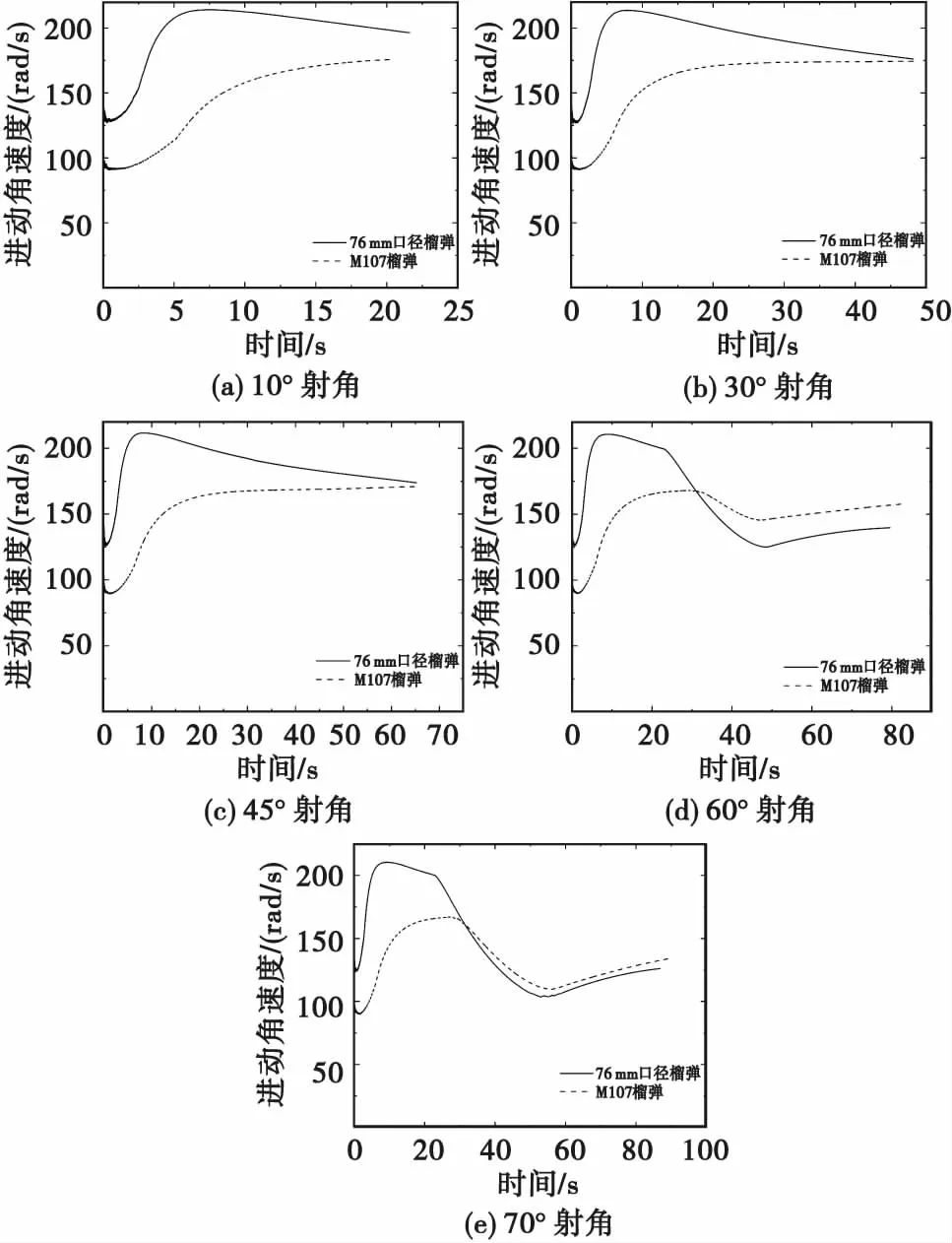
图12 不同射角下76 mm口径榴弹和M107榴弹进动角速度随时间变化规律Fig.12 The precession angular velocity of the 76 mm caliber grenadeand M107 grenade at different firing angles versus time

从图12可看出:弹丸以45°以下射角射击时,进动角速度持续增大或先增大后持续减小;而以45°以上射角射击时,进动角速度在弹道顶点之前先增大后减小,靠近弹道顶点附近有较大的衰减趋势,在弹道顶点之后略有增大。

将解算弹丸六自由度刚体外弹道模型得到的弹丸射程、转速衰减规律和偏流等规律与公认的经验公式、弹丸质心运动方程解算得到的外弹道规律对比,验证了弹丸六自由度刚体外弹道模型的可信性。上述规律是由微分方程组求解的结果,所有诸元与变量都是相互关联的。若射程和转速规律没有异常,则可以说明其他诸元与变量应该也没有异常。如果其他诸元与变量有异常,不可信,那么所得到的射程、转速、偏流和射高也不可能正常。因此,可认为通过解算弹丸六自由刚体外弹道模型得到的引信力学环境是可信的。

3 结论

本文以155 mm口径加榴炮M107榴弹和76 mm口径舰炮榴弹为例,在弹丸六自由度刚体外弹道模型的基础上进一步得到了155 mm口径加榴炮M107榴弹和76 mm口径舰炮榴弹的爬行过载、章动变化规律、进动变化规律和自转角速度衰减规律。结果表明:中大口径火炮旋转弹丸以45°以下射角射击时,最大章动角在全弹道上逐渐衰减;而以45°以上射角射击时,最大章动角总体上也是在全弹道上逐渐衰减,但在弹道顶点附近会略有增大。由弹丸刚体外弹道模型解算得出的中大口径火炮旋转弹丸外弹道自转角速度衰减规律,与幂函数经验公式估算结果以及少有的落点测试结果较为接近。