一种低功耗架构下毫米波信道估计算法研究

王 刚,邓诗蕾,陈顺利,向黎藜,邹 波,李心安

(1.国家电网有限公司 重庆市电力公司,重庆 400000;2.重庆邮电大学 通信与信息工程学院,重庆 400065)

0 引 言

随着智能终端和无线设备的普及,无线通信技术正面临频谱危机,目前在低于6 GHz频率下运行的无线网络将无法满足不断增长的带宽要求[1]。毫米波频段(30～300 GHz)提供了大数量级的物理频谱,是下一代移动通信的首要选择[2]。但是,毫米波具有极高的路径损耗、严重的大气衰减和雨衰[3]。为了降低毫米波的固有特性对通信系统性能的影响,大规模多输入多输出(multiple-input multiple-output, MIMO)系统通过在基站侧配置大量天线(多达数百根)生成定向波束,能够有效地克服路径损耗。与此同时,毫米波极短的波长使得同样大小的阵列能够配备更多的天线[4]。

毫米波技术与大规模MIMO系统的结合带来以下问题:①大规模MIMO系统增大了信道矩阵维度,成倍地增大了信道估计算法的计算复杂度,无法满足实际工程的实现需求;②天线数量增多意味着射频链路的增加,同时毫米波频段的模数转换器(analog-to-digital converter,ADC)以及低噪放大器等导致器件功耗较大[5]。研究表明,ADC的功耗与系统带宽呈线性正相关,与分辨率呈指数正相关[6]。因此,为了降低系统功耗,一种自然的想法是降低ADC的分辨率。但是,低分辨率ADC带来较大的量化误差,从而影响信道估计的精度。如何根据低分辨率量化后的观测值估计高维毫米波信道矩阵,是亟待解决的问题。

为了解决以上问题,国内外学者相继提出了许多方法降低量化噪声对信道估计准确性的影响,主要包括3类。第1类方法将非线性量化模型转化为线性模型,如文献[7]利用Bussgang分解将非线性量化噪声等效为具有相同一阶和二阶统计特性的线性量化噪声模型,设计了一种基于该线性模型的最小均方误差(minimum mean square Error, MMSE)意义下最优的信道估计算法,并给出了系统容量的闭合表达式。第2类方法模拟量化过程,同时利用毫米波信道的稀疏性,如文献[8]将观测到的量化测量值作为不可获得的非量化测量值的模约束条件,利用毫米波信道的稀疏性作为目标函数,根据其追踪(basis pursuit, BP)算法思想求解该优化问题。第3类方法旨在通过量化后的观测值估计非量化观测值,如文献[9]利用毫米波信道在角度域和延迟域的联合稀疏性,将信道估计问题转化为含噪量化稀疏信号重构问题,结合最大化期望算法(expectation maximization,EM)和向量化近似消息传递算法(vector approximately message passing,VAMP),提出EM-VAMP算法求解该重构问题。上述算法中,第1类算法涉及大量高维矩阵的伪逆运算,难以实际应用;第2类算法优化问题中通常包含单位模约束,无法确保收敛于全局最优解,数值不稳定;第3类算法具有可接受的时间复杂度与估计准确性,但当ADC分辨率提高时,由于VAMP算法无法直接利用量化观测值,系统性能提升有限。本文充分考虑第2类算法和第3类算法的优点,结合梯度下降(gradient descent,GD)算法和EM算法,提出一种两阶段信道估计算法。首先,利用量化过程构造优化问题,采用归一化梯度下降(normalized gradient descent,NGD)算法估计支撑集;然后,根据估计的支撑集将信道估计问题降维;最后,采用EM算法降低量化误差,估计信道复增益。

1 系统模型

低分辨率ADC下MIMO系统模型如图1所示。

图1 低分辨率ADC下MIMO系统模型Fig.1 System model under low-resolution ADC

图1中,发送天线接收天线分别为Nt、Nr个阵元的均匀线阵,阵元间隔均为波长的一半。接收端每个射频链路配备两个低分辨率ADC,分别用于量化接收信号的同相分量和正交分量。窄带平坦衰落毫米波物理信道可表示为[10]

(1)

(2)

(2)式中,(·)T表示转置运算。

毫米波信道矩阵的稀疏网格化可表示为[11]

(3)

(3)式中:UR∈Nr×Nr表示接收端字典矩阵;HS∈Nr×Nt表示稀疏等效信道矩阵;UT∈Nt×Nt表示发送端字典矩阵。

等效信道矩阵HS元素所在的行对应到达角的值、列对应离开角的值,元素值对应毫米波信道复增益。信道矩阵的稀疏网格化表示将信道估计问题转化为等效信道矩阵支撑集和支撑集对应元素值的估计。

发送端发送训练矩阵X∈Nt×P,P表示训练长度,接收端根据观测到的量化接收信号估计毫米波信道,表示为

(4)

(4)式中:Q(·)表示量化操作;R∈Nr×P表示量化后接收矩阵;Y∈Nr×P表示量化前接收矩阵;FR∈Nr×Nr表示接收端预编码码本;FT∈Nt×Nt表示发送端预编码码本;N∈Nr×P表示信道噪声矩阵。将接收矩阵列向量化可得

vec(R)=vec(Q(Y))=

(5)

(5)式中:vec(·)表示列向量化;(·)*表示取共轭。为了表达方便,将(5)式记为

r=Q(y)=Q(Φh+n)

(6)

(6)式中:r∈NrP×1表示量化后观测向量;y∈NrP×1表示量化前接收信号;Φ∈NrP×NtNr表示感知矩阵;h∈NtNr×1表示稀疏等效信道向量;n∈NrP×1表示噪声向量,每个元素服从均值为0方差为的复高斯分布且元素之间相互独立。

由(6)式可知,毫米波信道估计问题转化为含噪量化稀疏信号重构问题:已知r和Φ,求解h。

2 两阶段信道估计算法

毫米波信道在角度域具有稀疏性,本文算法利用该特性将信道估计问题分为2个阶段。第1阶段将毫米波信道支撑集估计问题构造为优化问题,并提出NGD算法求解;第2阶段利用估计的支撑集,将信道估计问题降维,利用改进的EM算法得到非量化接收信号y的最大似然估计(maximum likelihood,ML),最后计算毫米波信道的最小二乘估计。

2.1 支撑集估计

量化后接收信号r实际上反映了Φh的取值范围,利用毫米波信道在角度域的稀疏性作为约束条件,即在满足约束条件的所有可行解中寻找最稀疏解,优化问题为

min‖h‖1

s.t.Φh-l≥0

-Φh+u≥0

‖h‖2=1

(7)

(7)式中,l和u分别表示接收信号的下界和上界。等式约束条件可避免优化问题收敛于平凡解,与此同时,等式约束条件缩小了优化问题的可行解集,不等式约束可看作超平面分割出的半空间,可行解集由半空间之间的并集缩小为单位球内半空间之间的并集。模约束条件会影响信道向量的准确性,由于该阶段只需要确定支撑集,模约束条件引入的信道向量估计误差不影响支撑集的判断[12]。

(7)式所示优化问题的松弛优化问题为

s.t. ‖h‖2=1

(8)

(8)式中:(·)i表示取向量的第i个元素;f(x)≜x2μ(-x)/2为单边二次罚函数,μ(x)为阶跃函数;λ为松弛因子,若松弛因子趋于无穷大,优化问题与其松弛优化问题收敛于相同的最优解。

定义代价函数为松弛优化问题的目标函数,表示为

(9)

对代价函数求一阶偏导数可得

(10)

(10)式中,(‖h‖1)′、f′(x)满足

值得注意的是,hi=0时导数(‖h‖1)′不存在。本文使用收缩函数S(x)近似l1范数的导数,收缩函数定义为

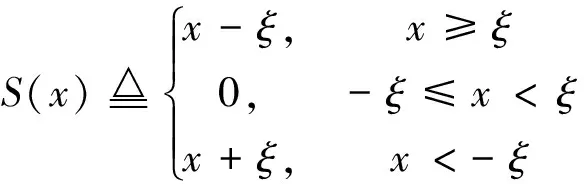
(11)

(10)式中,ξ为一较小正实数。

本文提出NGD算法求解(8)式所示松弛优化问题,算法伪代码如算法1所示。算法1中,步骤1选取任意单位模向量初始化信道向量,若选取h0=Φ†r,算法收敛速度较快,但伪逆运算复杂度较高;步骤4计算代价函数J(h)中罚因子项的梯度;步骤5执行罚因子项梯度下降;步骤6执行代价函数J(h)中l1范数项梯度下降;步骤7归一化局部最优解。

算法1NGD算法

输入:感知矩阵Φ,下界l,上界u,梯度下降步长δ,门限值ε,最大迭代次数kmax

输出:信道向量支撑集

1.选取任意单位模向量h0

2.初始化迭代变量k=0

while ‖hk-hk-1‖2>εandk

3.更新迭代变量k=k+1

end while

8.计算hk的支撑集

2.2 信道复增益估计

文献[13]基于迭代思想提出了最大化期望算法,降低了1比特ADC量化误差对毫米波信道估计准确性的影响。1比特ADC只保留观测值的符号信息,仍旧会引起较大的量化误差,本文做了两点改进:①利用估计出的支撑集将信道估计问题降维,降低其时间复杂度;②将1比特量化拓展到多比特量化情况。

第1阶段估计的支撑集可将问题模型(6)降维为

rsupp=Q(ysupp)=Q(Φsupphsupp+nsupp)

(12)

(12)式中,下标supp表示抽取对应元素,组成子向量或子矩阵。

采样后接收信号的ML估计为[9]

(13)

(14)

(14)式中:p(·)表示对应随机变量的概率密度函数;Pr{·}表示所包含事件的概率。(14)式的分母可展开为

(15)

(15)式中,erfc(·)表示互补误差函数,(14)式的分子通过分部积分化简为

(16)

将展开的分子分母代入(14)式可得

(17)

在前面的分析中,假设信道向量已知,但实际信道向量的值未知。EM算法通过迭代逼近,伪代码如算法2所示。算法2中,步骤1初始化信道向量,不同于NGD算法,降维后的信道估计问题维度为毫米波信道路径数,伪逆运算复杂度较低;步骤4执行EM算法中的期望步骤;步骤5对降维的信道向量做最小二乘估计。

算法2EM算法

输入:感知矩阵Φ,下界l,上界u,门限值ε,最大迭代次数kmax,量化后观测值r

2.初始化迭代变量k=0

while ‖hsupp,k-hsupp,k-1‖2>εandk

3.更新迭代变量k=k+1

4.取期望yEM=E[y|r]

end while

2.3 算法复杂度分析

本文NGD-EM算法的两个阶段串行实现,可分别计算它们的复杂度。第1阶段的算法复杂度集中在矩阵运算,因此为O(NrP)[9]。第2阶段求出了条件期望的闭合解,算法复杂度最高的运算为矩阵乘法和互补误差函数。互补误差函数可采用查表法,其算法复杂度为线性,矩阵乘法的算法复杂度也为O(NrP)。因此,所提算法的时间复杂度为O(NrP)。表1给出了对比算法的时间复杂度。

表1 计算复杂度对比

3 仿真分析

本节验证NGD-EM算法在32×8窄带毫米波MIMO系统的性能。毫米波信道在角度域具有稀疏性且其元素服从伯努利-高斯混合分布。训练矩阵为Hadamard矩阵的列,训练长度为16。选取性能指标为归一化均方误差(normalized mean square error,NMSE),定义为

(18)

图2 LoS信道模型下性能对比Fig.2 NMSE comparison between NGD-EM and EM-VAMP under LoS

图3 2径NLoS信道模型下性能对比Fig.3 NMSE comparison between NGD-EM and EM-VAMP under 2-rays NLoS

首先,NGD-EM算法比EM-VAMP算法具有更高的准确性,尤其在更高ADC分辨率情况下。这是因为本文算法的第2阶段计算了采样后接收信号的ML估计,同时得到了毫米波信道向量的LS估计,这在范数意义下是最优的。除此之外,NGD-EM算法比EM-VAMP算法计算复杂度更低。

其次,接收端采用1比特ADC时,随着SNR升高,NMSE也会提高。这是因为1比特ADC只保留接收信号符号信息,原始值过大或过小都会造成较大的量化误差,这种现象被称为随机共振[9,12-13]。

最后,NGD-EM随ADC分辨率的提高显著提升,尤其是在2比特到3比特之间时。而3比特到4比特之间时,本文算法准确性也有相似特性,这也验证了文献[6]中,ADC分辨率为3比特或4比特时实现系统能量-效率最大化的结论。因此,可以得出结论,在接收端使用3比特ADC既能保证信道估计的准确性,又能满足较低功耗的要求。

4 结束语

本文利用毫米波信道在角度域的稀疏性,提出了一种低功耗架构下窄带毫米波MIMO系统的信道估计算法。首先,利用量化过程构造优化问题,采用梯度下降算法估计支撑集;然后,根据估计的支撑集将信道估计问题降维;最后,采用最大化期望算法降低量化误差并估计信道复增益。仿真结果表明,所提算法在估计精度和时间复杂度上均优于已有算法,具有十分重要的现实意义。