基于排队论的OLTP模型研究

柳晶晶

摘要：联机交易（OLTP）系统是一种典型的计算机应用系统，虽然使用数量众多，但其系统设计一般停留在感性阶段，多是通过试验和测试手段考查其设计的有效性，性能调优基本依靠技术人员的经验，缺乏系统性的理论指导。为了提高OLTP系统设计的可靠性和稳定性，从排队理论的角度进行了抽象和分析，并以大额支付系统为例给出了OLTP系统的处理模型，形成理解和讨论OLTP系统内部处理机制的基础，有助于实现从知道怎么做到知道为什么这么做的转变。

关键词：联机交易系统；排队论；随机过程

一、前言

排队论[1]是一门专门研究排队问题的运筹学分支。排队论的起源可以追溯到1909年爱尔朗（A. K. Erlang）的论文，该论文的发表为后来排队论的发展奠定了坚实的基础。在绝大多数的排队系统中，顾客到达和服务时间都是随机的。排队过程通常是一个随机过程，排队论又称“随机服务系统理论”。排队论在计算机性能分析和通信网的定量分析方面占有极重要的地位。一个计算机或网络实际可看成一个复杂的排队系统[2]。

二、OLTP系统的排队模型

排队模型需要确定排队系统的各项特征，如平均等待时间、平均队长等，或是构建某个服务系统以满足特定的顾客服务水平。

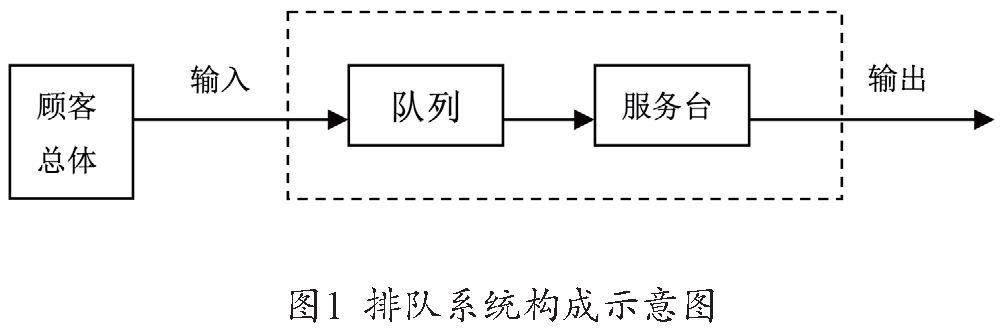
（一）排队系统的基本构成

排队系统通常由输入、队列、服务台和输出四部分构成，可以用图1来加以描述。

（二）排队系统的分类描述

肯达尔（Kendall）通过由斜线分割开的6项代码来表示排队模型。前两项为字符码，分别表示到达过程和服务过程的分布形式。第三、四、五项是数字，分别代表服务台数目、系统的容量和顾客总量。最后一项表示排队规则。

（三）单服务器排队系统模型

泊松到达过程、负指数服务时间分布、只有一个服务员的排队系统模型为M/G/1。其中，M代表泊松输入或服务时间服从负指数分布，G代表一般的服务时间。对于M/G/1模型，服务时间 的分布是一般的（但要求期望值E[T]和方差Var[T]都存在）。为了达到稳态，ρ<1这一条件是必要的，其中ρ=μ/λ。对于M/G/1排队系统，系统中逗留的平均顾客数和平均逗留时间仅与顾客平均到达率λ、平均服务时间1/μ及服务时间的方差Var[T]有关，而不需知道服务时间的分布情况。

（四）多服务器排队系统模型

1.M/M/c/∞/∞模型

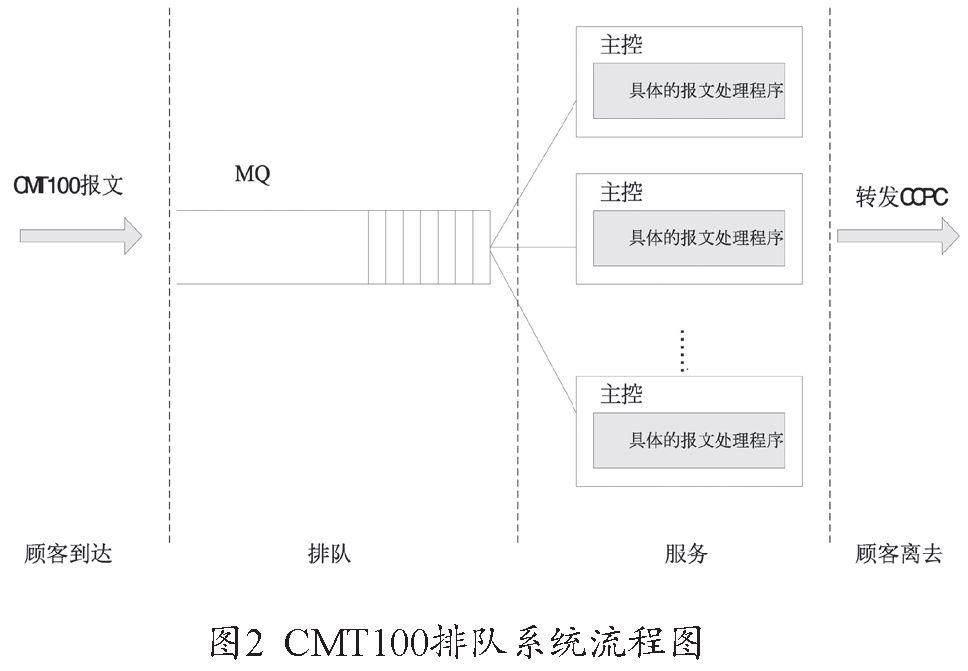
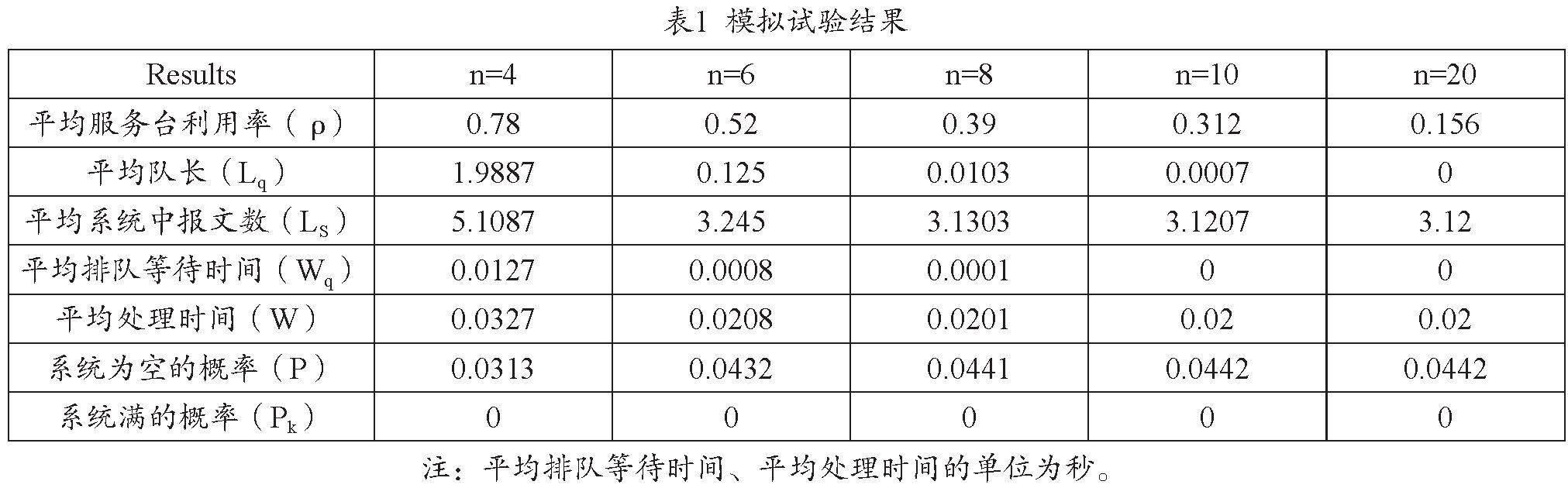
M/M/c（c≥2）是多服务台的等待制排队系统，它的各种特征的规定和假设与M/M/1模型基本相同。假定c个服务台并联排列，各服务台独立工作，其平均服务率相同，即μ1=μ2=…=μc=μ。因此，当n≥c时（n为系统中的顾客数量），该系统的平均服务率为cμ；当n

2.M/M/c/N/∞模型

该系统的容量最大限制为N（≥c），当系统中顾客数n已经达到N时，再来的顾客将被拒绝，其他条件与标准的M/M/c相同。

三、OLTP系统的排队模型实例

从OLTP系统的角度看，大额支付系统是典型的OLTP系统。下面将以大额支付系统在国家处理中心（NPC）节点的处理为例，在分析现有处理流程的基础上，整理并抽象其排队模型。

（一）大额支付系统的处理流程

大额支付系统NPC使用CICS交易中间件保证交易的完整性；使用MQ传输中间件实现报文的传输；在开放和主机平台上分别使用ORACLE和DB2，负责数据的存储和管理。MCTL是大额支付系统应用的主控程序。当CICS启动时同时启动MCTL。在CICS活动期间MCTL一直处于活动状态。大额支付系统城市处理中心（CCPC）向NPC的MQ网关（MQGW）发送报文。MQGW收到CCPC发来的报文，进行报文分配，并将报文转发给大额应用服务器。大额应用服务器MQ本地队列收到CCPC发来的CMT100报文，触发MCTL。MCTL根据报文的种类，调用相应交易服务程序。大额支付系统一般大额业务（CMT100）报文的并发主要处理体现在以下几个方面（忽略了应用服务器的并发处理）：

1.主控程序的并发

主控程序的最大并发数：主控程序MAINSVR是CMT100报文处理的入口。MAINSVR服务程序在CICS中的交易名是MCTL。MCTL采用MQ触发机制，其基本功能是读取NPC本地队列里的报文，并调用相应的程序进行处理。在大额CICS REGION中，通过RD中的MINSERFER和MAXSERVER定义了总的程序并发处理能力。MCTL作为CICS REGION中由TCLASS定义的其中一类交易，在RD中进一步定义了MCTL可以并发的最大个数（由ClassMaxTasks参数确定）。在大额支付系统中，MCTL的最大并发数为20。主控程序实际的并发数：主控程序由MQ触发。大额支付系统采用的是MQ First（trigdpth 1，trigint 500）触发方式。在该交易调用机制下，MQ队列触发器类型设置为First，当队列中满足条件的消息从0变到非0时会产生一条触发消息，MQ 队列的Monitor会调起主控处理程序处理队列中的消息，直到队列为空为止。在某些情况下，当队列不为空时，MQ系统隔trigint时间后也会产生一条新的触发消息。每一个触发消息都会触发一个主控，由于CMT100报文达到的随机性，可能会启动多个主控，但实际并发的主控个数小于等于主控的最大并发数。

2.消息服务的并发

一个主控触发后，主控依次读取本地队列中的所有消息，直到队列中没有消息为止。因为主控是同步调用消息处理程序（HNSV1000），所以在一个主控范围内，消息处理程序是串行的，没有并发问题。

（二）排队系统表述

如果将CMT100报文视为排队系统中的顾客，将NPC节点本地队列视为排队系统中的队列，将主控视为排队系统中的服务台，CMT100的排队系统流程图见图2。

（三）模型假设

按照排队理论和以上的分析，做出如下假设：

1.顾客的特性

（1）由于OLTP系统一般处理的交易是巨量的，因此可以近似认为顾客总体是无限的。

（2）在同一时点上只能有一个顾客到达。

（3）顾客到达是相互独立的。

（4）顾客到达的时间间隔是随机的。

2.队列的特性

（1）CMT100排队系统中，只有一个队列。

（2）如果所有服务台都正在被占用，顾客不会选择随即离去，而是排队等待。

（3）生产系统中队列的深度是固定的，因此是有限队列。

3.服务台的特性

（1）主控程序可以并发。排队系统中可以有一个或多个服务台。如果是多服务台，各服务台可以串联、并联或混联。实际并发的主控个数具有一定的随机性。

（2）主控服务一次只能处理一个报文。

（3）主控服务的处理时间是随机的。

（4）如果主控服务的服务时间分布和特征参数不随时间的变化而变化，即是平稳的。

（5）CMT100的服务规则是先到先服务（FIFO）。

4.输出的特性

CMT100处理完成后，即刻转发CCPC，因此以上排队系统是一个开环系统。

（四）排队模型

要建立排队模型，除了以上的假设，还需明确以下三个问题：

1.顾客到达的规则

顾客到达是随机的，因此需要确定单位时间的顾客到达数或相继到达时间间隔的概率分布。假设顾客到达是符合泊松分布的随机过程，（严格意义上，应根据实际生产数据，进行x2假设检验）。

2.服务台的个数

服务台数即为MCTL最大并发个数，实际上可以得出此OLTP系统业务处理的最高效率，包括吞吐量、平均等待时间、平均队列长度等技术指标。

3.服务的规则

最简单的服务时间分布是负指数分布（严格意义上应根据实际生产数据，进行x2假设检验），这种情况下，平均服务率一个参数就完全描述了整个服务过程。平均服务率μ可以用测试的方法确定，即单个主控的处理速率。

因此，以上OLTP系统的排队模型可以确定为M/M/c/N/∞/FIFO，其中c为MCTL的最大并发个数，N为本地队列的最大长度与c之和。

（五）排队模型的模拟试验分析

除了以上给出的解析方法，下面以模拟试验的方法对其进行分析。假设在λ＝156笔/秒，μ=50笔/秒的情况下，当n<4时，由于nμ<λ，即ρ>1，因此队列长度会不断增大，以至于造成队列满的情况。在模拟时，仅模拟n=4，6，8，10，20的情况，此时ρ<1，不会形成无限队列，由此得出排队系统的统计平均指标如表1所示。

在n=4时系统状态（pn）的概率分布见图3。

在n=20时系统状态（pn）的概率分布见图4。

在假定CMT100报文平均到达率λ＝156笔/秒以及NPC服务器平均服务率μ＝50笔/秒不变的情况下，随着并发服务台的个数增加，有如下结论：

1.大额支付系统平均队长近似为零。也就是说，在假定的业务量和系统设计处理容量的条件下，业务一旦到达，可即刻处理，几乎不需排队等待。由于几乎不存在业务排队，因此业务排队撤销也是没有必要的。大额支付系统的这种设计，实际上是通过增加系统处理容量，以较低的设备使用效率代价换取了业务处理的最大实时性。

2.当并发服务台的个数n≧4后，系统的平均排队等待时间几乎可以忽略，平均处理时间也基本相同，不会随着并发服务台的个数增加而明显增加。因此在不考虑资源瓶颈（如CPU、内存、CICS并发进程、清算账户等）的限制和并发服务台之间同步和冲突开销的前提下，大额支付系统理想的吞吐量峰值（吞吐量峰值＝n×1/W）会随着并发服务台的个数增加而近似线性的增加。

3.n≧4时，大额支付系统的系统状态趋于稳定，不会随并发服务台个数的增加而有明显的改善。

4.由于CCPC的处理逻辑不涉及清算账户资源瓶颈，因此其处理模型可以用无冲突的M/M/c/N/∞/FIFO模型很好地刻画，此时实际并发的主控进程数就可以近似认为是n，提高CCPC处理容量的有效方法之一就是提高并发主控进程数量，从排队系统的角度，也很容易解释为什么CCPC的处理性能可能远远大于NPC的原因。

四、结语

排队模型是目前计算机系统性能评价中应用最广的一种分析模型。基于经典随机过程假设的排队理论通常被称为“马尔可夫排队网络”。尽管这些假设有时是不成立的，例如参数是随时间变化的、作业是相关的等，但是Buzen[3]和Denning[4]研究证明，马尔可夫排队模型的结果可以从一组完全不同的假设推导出来，这些假设能够直接检验，而且实际系统多半满足这些假定。因此也就解释了即便经典排队理论的大部分假设与实际情况不符，但排队模型刻画的实际系统还可以得到比较满意的结果的原因。

本文通过引入排队理论，以大额支付系统为例给出了联机交易系统的处理模型。排队模型给出了一种排队系统的解析方法，特别是那些符合马尔可夫排队网络假设的排队系统，其关键性统计指标是能够解析得出的，这些指标比较全面地、量化地描述了排队系统的特征，也给出了可能影响系统性能的关键要素。

参考文献

[1]《运筹学教材》编写组.运筹学[M].北京：清华大学出版社，1990.

[2]林生.计算机通信网原理[M].西安：西安电子科技大学出版社，1997.

[3]Buzen， Jeffrey P .Computational algorithms for closed queueing networks with exponential servers[J].Communications of the ACM， 1973， 16（9）：527-531.

[4] Denning P J ， Buzen J P .The Operational Analysis of Queueing Network Models[J].Acm Computing Surveys， 1978， 10（3）：225-261.