乘性色噪声激励下广义分数阶van der Pol-Duffing振子的随机分岔分析
2023-04-29王媛张建刚盛正大
王媛 张建刚 盛正大
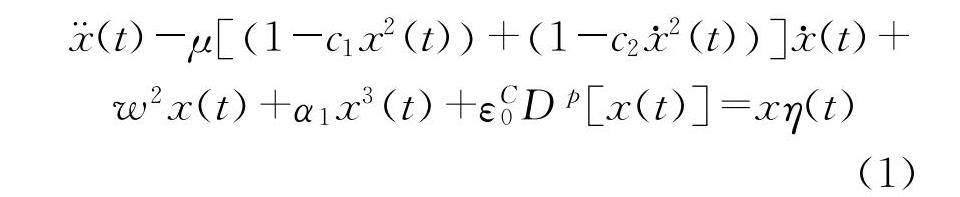
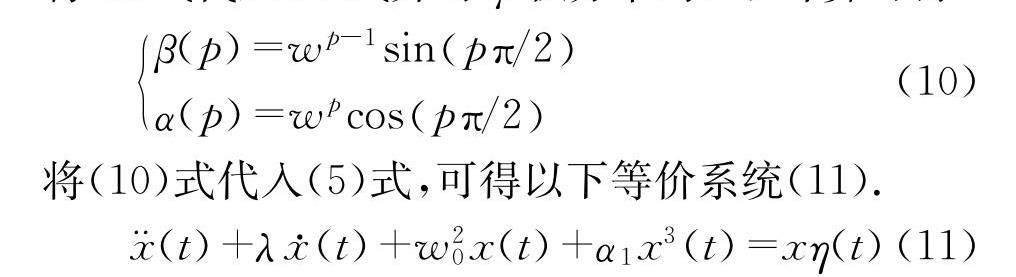
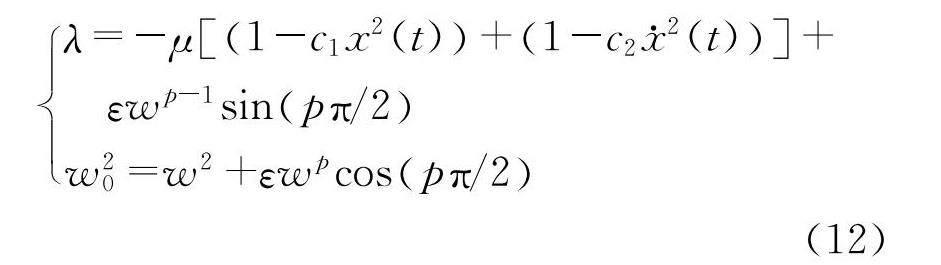
摘要:本文研究了在乘性色噪声激励下含分数阶导数项的广义Duffing振子的随机分岔. 首先, 利用一种回复力和阻尼力的线性组合等效替换系统中的分数阶导数项; 其次, 对系统中的三次项进行线性化处理,利用最小均方误差原理,将系统转变成整数阶系统,由随机平均法求得系统的稳态概率密度函数; 最后, 通过拟不可积Hamilton系统随机平均法得到系统不变测度的最大Lyapunov指数,并对系统进行随机D-分岔和P-分岔分析. 研究发现,分数阶导数阶数、噪声的自相关时间等参数的改变可以诱发系统发生随机P-分岔.
关键词:乘性色噪声; 分数阶; 广义Duffing振子; 随机分岔
收稿日期: 2023-05-08
基金项目: 国家自然科学基金 (61863022); 甘肃省自然科学基金重点项目(23JRRA882)
作者简介: 王媛(1999-), 女, 山西运城人, 硕士研究生, 主要研究方向为非线性动力学. E-mail: 1244468171@qq.com
通讯作者: 张建刚. E-mail: zhangjg7715776@126.com
Stochastic bifurcation analysis of generalized fractional order
van der Pol-Duffing oscillators under multiplicative color noise excitation
WANG Yuan, ZHANG Jian-Gang, SHENG Zheng-Da
(School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou 730070, China)
This article investigates the stochastic bifurcation of a generalized Duffing oscillator with fractional derivative term under multiplicative colored noise excitation. Firstly, a linear combination of restoring force and damping force is used to equivalently replace the fractional order derivative term in the system. Secondly, the cubic term in the system is linearized, the system is transformed into an integer order system by using the principle of minimum mean square error, the steady-state probability density function of the system is obtained by the stochastic averaging method. Finally, the maximum Lyapunov exponent of the invariant measure of the system is obtained by the stochastic averaging method of quasi-non-integrable Hamilton system, and the stochastic D-bifurcation and P-bifurcation of the system are analyzed. It is found that the changes of fractional derivative order, autocorrelation time of noise and noise intensity can induce stochastic P-bifurcation of the system.
Multiplicative colored noise; Fractional order; Generalized Duffing oscillator; Stochastic bifurcation
1 引 言
随机分岔是在噪声作用下非线性系统产生的一种独特的随机动力学行为, 当非线性系统在随机参数发生改变时, 系统形态会发生如平衡态、平衡运动、以及其他的相关渐近运动的变化. 随机分岔有两种分岔类型, 分别是P-分岔和D-分岔. P-分岔指的是随着参数的变化,系统不变测度的概率密度函数的峰值个数、位置以及形状发生改变, 例如从无峰变成单峰或者从单峰变成双峰等[1]; D-分岔指的是从一组参考测度中可以分岔出新的不变测度, 一般是用最大Lyapunov指数的正负号变化来判定.
对随机分岔的相关研究可以追溯到上世纪八十年代, 如Arnold[2]从数学的角度对随机分岔进行了论述. 随机分岔在神经网络[3]、结构工程[4]以及生物医学[5]等领域也有了一定的研究. 近年来, 人们对随机系统的分岔问题进行了研究. 如,Hu等[6]研究了含有分数阶导数阻尼项的非线性系统在窄带噪声激励下的随机分岔问题;吴志强等[7]利用奇异性理论,研究了噪声强度等对三稳态van der Pol-Duffing系统的随机P-分岔的影响;Yang等[8]利用预测校正法, 研究了一种双稳态分数阶系统在白噪声激励下的随机P-分岔问题.
分数阶微积分具有时间记忆性, 并且可以很好地描述黏弹性材料的特征, 因而被广泛应用于工程领域. 以经典的Duffing振子为例, 该系统在外部激励的作用下会产生混沌、共振、分岔等动力学行为, 在加入分数阶项后该系统将更贴近现实系统的描述, 因此研究分数阶系统具有一定的意义. 近年来学者们对分数阶Duffing振子进行了一系列研究. 如,王军等[9]利用Melnikov方法, 研究了分数阶分段Duffing振子在谐波激励下的混沌运动;Yan等[10]从理论和数值上研究了具有分布延迟的Duffing振子在任意分数阶谐波共振下的振动机理;唐建花等[11]研究了广义分数阶van der Pol-Duffing振子的隔振效果和力传递率, 研究发现不同参数对系统的隔振效果影响也不同.
可见学者们对随机激励下分数阶Duffing振子的研究较多, 而对广义分数阶Duffing振子在乘性噪声激励下关于随机分岔的研究还未见报道. 因此, 本文提出一种具有非线性阻尼项的广义分数阶van der Pol-Duffing振子, 研究其在特殊乘性色噪声激励下的随机D-分岔和P-分岔, 并利用随机平均法对该系统的概率密度函数曲线图进行分析. 研究表明, 参数的变化可以影响系统的分岔行为.
2 具有分数阶导数阻尼项的广义van der Pol-Duffing振子
广义分数阶van der Pol-Duffing振子可用以下形式表示.
其中,μ,c1,c2为上述系统中的非线性阻尼系数;w为系统的自然角频率;ε为分数阶导数项的系数;α1为非线性刚度;η(t)是高斯色噪声,且η(t)的均值和方差满足(2)式,其功率谱密度满足(3)式(其中w=1).
其中,D为噪声强度;τ为色噪声的自相关时间;C0Dp[x(t)]为在Caputo意义下的x(t)关于t的p(0≤p≤1)阶分数阶导数, 其定义[12]如式(4)所示.
这里, n-1
为方便计算, 由文献[13-15]可知, 可以将分数阶导数项转换为阻尼力和回复力的线性组合, 进而得到以下的等效系统.
其中, β(p),α(p)分别是等效阻尼力和回复力的系数.
系统(1)和系统(5)之间的误差e为
由最小均方误差的必要条件[16]可知
将(6)式代入(7)式可得
将(1)式的解设为以下形式.
将(9)式代入(8)式并对φ积分平均, 经计算可得
将(10)式代入(5)式,可得以下等价系统(11).
其中,
将上述系统中的三次刚度项通过线性化进行处理,则等效系统(11)又可变为以下形式[17].
系统(11)和系统(13)之间的误差为
为确定系统(13)中的两个系数βa和αa,可将式(13)的解设为以下形式.
其中, w20=w2+εwpcospπ/2. 为使式(14)的误差最小,利用广义的谐和平均法,来确定两个系数βa和αa.
将(16)式代入(13)式,可得以下等价系统(17).
其中,
为进一步确定系统(17)的解, 引入如下变换[18].
其中, a(t),θ(t)分别为系统的幅值过程和相位过程;f为系统的频率. 根据广义van der Pol变换, 将(19)式代入(17)式, 由确定性平均法可得以下随机微分方程.
其中,
运用随机平均法[19],可将(20)式转化为如下的平均It随机微分方程.
其中, W(t)是标准的维纳过程,且漂移系数和扩散系数分别为
由(22)式及(23)式可知, 方程中的da的表达与θ(t)是相互独立的, 因此系统对应幅值的Fokker-Planck-Kolmogorov(FPK)方程如下.
若系统满足边界条件
则可得系统幅值的稳态Probability Density Function (PDF).
其中, C为归一化常数, 且满足
3 随机分岔
3.1 D-分岔
将(23)式代入(22)式中,可得一维的Markov过程用以下方程表示.
这一节主要通过观察系统的稳态PDF曲线图的峰值个数来判断系统是否发生了随机P-分岔. 选取一组基本参数[20]: μ=0.01, c1=3, c2=2, w=1, ε=0.2, α1=1,重点讨论分数阶导数阶数、噪声时滞以及噪声强度这几个参数对该系统发生随机P-分岔的影响.
固定参数D=0.22, τ=0.3. 根据式(42)画出在不同分数阶导数阶数p下系统的模态分布(见图1~图3). 如图1所示, 当p=0.1时, 系统的稳态概率密度函数图呈单峰状态, 随着参数p的增大, 稳态PDF曲线图又由一峰一谷状变成无峰状. 如图2所示, 与之相对应的联合PDF图也出现了由火山口型状向无峰状的跃迁. 观察图3中暗红色处所对应的振幅分别为0.4、1.4和6.8, 最终将趋于一个极限值. 如图3所示, 当p=0.1时, 系统中存在一个较为稳定的极限环; 当p=0.2时, 系统中同时出现了平衡点与极限环; 当p=0.24时, 系统中仅出现平衡点; 可见系统的稳态响应发生了明显变化. 这说明随着阶数p的变化, 系统会发生随机P-分岔行为.
固定参数D=0.22,p=0.18. 根据式(42)画出在不同自相关时间τ下系统的模态分布(见图4~图6). 如图4所示, 当τ=0.26时, 系统的稳态概率密度函数图仅在约a=0.65处出现一个峰值; 当τ=0.33时, 相应的稳态概率密度函数图在离原点较远处有一峰值, 并在原点附近呈Dirac函数形式; 当τ=0.51时, 相应的稳态概率密度函数图呈Dirac函数形式. 相对应各个图的联合概率密度函数图, 观察图5a与图6a, 当τ=0.26时, 图中呈单峰状态, 此时系统中将存在一个较为稳定的极限环; 观察图5b与图6b, 当τ=0.33时, 图中呈一峰一谷状态, 系统中将同时出现平衡点与极限环; 观察图5c与图6c, 当τ=0.51时, 图中呈无峰状态, 系统中将只出现平衡点, 此变化说明系统经历了随机P-分岔. 这说明在色噪声的自相关时间τ变化时会使系统发生随机P-分岔行为.
固定参数τ=0.3,p=0.2. 根据式(42)画出在不同噪声强度D下系统的模态分布(见图7~图9). 如图7所示, 当D=0.9时, 系统的稳态概率密度函数图在约a=1.2处出现峰值, 系统呈单峰状态, 此时系统中只存在大幅度振动; 当D=0.26时, 系统的稳态概率密度函数图在离原点较远处有一峰值, 并在原点附近呈Dirac函数形式; 当D=0.2时, 系统的稳态概率密度函数图呈无峰状, 即系统经历了由单峰到无峰的跃迁. 如图8所示, 随着参数D的增大, 相对应的联合PDF曲线图所呈火山口的形状随之增大, 此时系统中将同时出现平衡点与极限环; 对应于图9, 可以清楚地发现当D=0.26时, 系统的平稳联合PDF曲线图出现两个较小的峰值变化, 当D=0.28和D=0.9时, 系统的平稳联合PDF曲线图仅出现一个峰值变化. 这说明噪声强度D的变化会使系统发生随机P-分岔行为.
4 结 论
本文主要研究了含分数阶导数项的广义Duffing振子在乘性色噪声激励下的随机分岔问题. 应用随机平均法, 通过替换其中的分数阶导数项, 并对方程中的三次项进行线性化处理, 利用均方误差最小原则和广义谐和平均法, 将原系统转换为整数阶系统, 最终求得系统幅值的稳态PDF. 通过分析系统发生D-分岔的临界条件, 以及用Matlab模拟系统的稳态概率密度函数p(a)、联合概率密度函数p(x,y)图, 详细分析了不同参数的改变对系统发生随机分岔的影响. 研究结果显示, 分数阶导数阶数p、噪声的自相关时间τ以及噪声强度D的改变均会使系统发生随机P-分岔. 利用这一结论, 可以更好地利用广义分数阶Duffing振子的动力学特性, 并将其应用到工程领域中, 以减少随机分岔造成的影响.
参考文献:
[1]朱位秋, 黄志龙, 应祖光. 非线性随机动力学与控制的哈密顿理论框架[J]. 力学与实践, 2002(3): 1.
[2]Arnold L. Random dynamical system [M]. Berlin: Springer-Verlag, 1988.
[3]Huang Z T, Yang Q G, Gao J F. Stochastic stability and bifurcation analysis on Hopfield neural networks with noise [J]. Expert Syst Appl, 2011, 38: 10437.
[4]Kumar P, Narayanan S, Gupta S. Bifurcation analysis of a stochastically excited vibro- impact Duffing-van der Pol oscillator with bilateral rigid barriers [J]. Int J Mech Sci, 2017, 127: 103.
[5]Huang Z T, Yang Q G, Cao J F. Stochastic stability and bifurcation for the chronic state in Marchuks model with noise [J]. Appl Math Model, 2011, 35: 5842.
[6]Hu F, Chen L, Zhu W. Stationary response of strongly non-linear oscillator with fractional derivative damping under bounded noise excitation [J]. Int J Nonlin Mech, 2012, 47: 1081.
[7]吴志强, 郝颖. 随机激励van der Pol-Duffing方程三峰P-分岔[J]. 中国科学: 物理学 力学 天文学, 2013, 43: 524.
[8]Yang J H, Miguel A F S, Liu H G, et al. Stochastic P-bifurcation and stochastic resonance in a noisy bistable fractional-order system [J]. Commun Nonlinear Sci, 2016, 41: 104.
[9]王军, 申永军, 张建超, 等. 一类分数阶分段Duffing振子的混沌研究[J]. 振动与冲击, 2022, 41: 8.
[10]Yan Z, Liu X. Fractional-order harmonic resonance in a multi-frequency excited fractional Duffing oscillator with distributed time delay [J]. Commun Nonlinear Sci, 2021, 97: 105754.
[11]唐建花, 李向红, 王敏, 等. 广义分数阶van der Pol-Duffing振子的动力学响应与隔振效果研究[J]. 振动与冲击, 2022, 41: 10.
[12]夏伟, 任芮彬, 罗懋康, 等. 具有质量涨落的双分数阶耦合谐振子系统的随机共振[J]. 四川大学学报: 自然科学版, 2023, 60: 021002.
[13]Shen Y, Yang S, Xing H, et al. Primary resonance of Duffing oscillator with fractional-order derivative [J]. Commun Nonlinear Sci, 2012, 17: 3092.
[14]Yang Y, Xu W, Gu X, et al. Stochastic response of a class of self-excited systems with Caputo-type fractional derivative driven by Gaussian white noise [J]. Chaos Soliton Fract, 2015, 77: 190.
[15]Xu Y, Li Y, Liu D, et al. Responses of Duffing oscillator with fractional damping and random phase [J]. Nonlinear Dynam, 2013, 74: 745.
[16]Liu W, Zhu W, Chen L. Stochastic stability of Duffing oscillator with fractional derivative damping under combined harmonic and Poisson white noise parametric excitations [J]. Probabilist Eng Mech, 2018, 53: 109.
[17]孙春艳, 徐伟. 含分数阶导数项的随机Duffing振子的稳态响应分析[J]. 振动工程学报, 2015, 28: 374.
[18]Liu T, Xu W, Xu Y, et al. Long-Term Dynamics of Autonomous Fractional Differential Equations [J]. Int J Bifurcat Chaos, 2016, 26: 1650055.
[19]Sun J, Huan R, Deng M, et al. A novel method for evaluating the averaged drift and diffusion coefficients of high DOF quasi-non-integrable Hamiltonian systems [J]. Nonlinear Dynam, 2021, 106: 2975.
[20]Li Y, Wu Z, Lan Q, et al. Stochastic bifurcation analysis of a bistable Duffing oscillator with fractional damping under multiplicative noise excitation[J]. Therm Sci, 2021, 25: 1401.
引用本文格式:
中 文: 王媛, 张建刚, 盛正大. 乘性色噪声激励下广义分数阶van der Pol-Duffing振子的随机分岔分析[J]. 四川大学学报: 自然科学版, 2023, 60: 064004.
英 文: Wang Y, Zhang J G, Sheng Z D. Stochastic bifurcation analysis of generalized fractional order van der Pol-Duffing oscillators under multiplicative color noise excitation [J]. J Sichuan Univ: Nat Sci Ed, 2023, 60: 064004.
