基于碳化硼慢化体和涂硼微结构中子探测器的通用中子能谱仪设计和解谱方法研究

颜筱宇 韩纪锋 黄宇 宋瑞强 徐子虚 刘星泉 曲国峰 张艺蓉 冷强钟 任飞旭 张鑫 陈蕾 刘吉珍

本文提出了一种基于碳化硼慢化体和涂硼微结构中子探测器的通用中子能谱仪设计方法，获得了计算最优慢化体厚度和探测器响应函数的通用公式，并用蒙特卡罗方法进行了验证和修正，可实现对中子能谱仪的快速设计. 该类能谱仪可实现各中子响应函数之间的解耦，使每个探测器对各个分立能量区间的中子最为敏感，具有较强适用性和灵活性. 基于该方法，我们设计了一个用于硼中子俘获治疗（BNCT）超热中子能谱测量的能谱仪，通过Gravel算法实现了中子能谱解析，并提出了一种具有良好普适性的基于响应函数的预置谱设置方法. 结果表明，该能谱仪对单能中子的峰位解析精度约为1%，对BNCT连续谱的解析均方差约为0.76%，具有较大技术优势和可行性.

中子谱仪；蒙特卡罗方法；少道解谱算法；硼中子俘获治疗

TL816+.3A2023.024003

收稿日期： 2022-10-17

基金项目： 四川省科技计划（2022NSFSC0831，2020YJ0313）; 中央高校基本科研业务费

作者简介： 颜筱宇（1996-）， 男， 山东曲阜人， 硕士研究生， 研究领域为中子探测.

通讯作者： 韩纪锋. E-mail： hanjf@scu.edu.cn

A general neutron spectrometer design method based on boron moderator and boron-coated micro-structure neutron detectors

YAN Xiao-Yu1， HAN Ji-Feng1， HUANG Yu1， SONG Rui-Qiang1， XU Zi-Xu2， LIU Xing-Quan1， QU Guo-Feng1， 3， ZHANG Yi-Rong1， LENG Qiang-Zhong1， REN Fei-Xu1， ZHANG Xin1， CHEN Lei1， LIU Ji-Zhen4

（1. Key Laboratory of Radiation Physics and Technology of the Ministry of Education， Institute of Nuclear Science and Technology， Sichuan University， Chengdu 610064， China;

2. Graduate School of Engineering， Osaka University， Osaka 565-0871， Japan;

3. Helmholtz Institute， Johannes Gutenberg-Universitt Mainz， Mainz 55099， Germany;

4. Nuclear Power Institute of China， Chengdu 610041， China）

In this paper， a general neutron spectrometer design method based on boron carbide moderators and boron-coated micro-structure neutron detectors is proposed. The formula for calculating the optimal moderator thickness and detector response function according to the neutron energy is obtained， which is verified and modified by the Monte Carlo simulation. The formula is able to realize the rapid design of the neutron spectrometer effectively. This kind of energy spectrometer can realize the decoupling of neutron response functions， so that each detector is most sensitive to neutrons in each discrete energy range， and has strong applicability and flexibility. An epithermal neutron spectrometer for boron neutron capture therapy （BNCT） is designed based on the proposed method， the response function of the spectrometer is calculated and the neutron spectrum unfolding is achieved by the Gravel algorithm. The results show that the resolution accuracy of the energy spectrometer to the peak position of monoenergetic neutrons is about 1%， and the analytical mean square error of the BNCT continuous spectrum is about 0.76%， which has great technical advantage and feasibility.

Neutron spectrometer; Monte Carlo method; Less channel spectrum unfolding algorithm; Boron neutron capture therapy

1 引 言

中子能谱的准确测量，在核医学、核物理基础研究、核工程、辐射防护和空间探测等领域有重要意义［1， 2］，也是反应堆、加速器等中子辐射场的关键参数［3］. 因此针对中子能谱仪的研发与中子能谱的测量等工作一直是该领域的研究重点和难点. 基于核反应法的Bonner多球谱仪具有灵敏度较高以及γ排除能力较好等优点，在中子能谱测量领域应用较为广泛［4-8］. 而中子响应函数是实现能谱测量的关键. 现有多球谱仪内各个探测器均对很宽能量区间内的中子有响应，响应曲线的能量区间重合度较高，仅在响应灵敏度上有所差异. 即， 各响应函数存在耦合，难以解耦，导致能谱解析困难、能量分辨率不高等问题. 南华大学的邹益晟等人［9］基于多球谱仪设计出一款解谱性能较好的基于闪烁体探测器的单球谱仪. 此仪器具有结构紧凑和操作简便的优点，但由于其响应函数能量区间重合度较高等问题导致能谱解析困难，其性能的进一步提升也受限于响应函数的固有特征. 目前，针对多球/单球中子谱仪的改进主要集中在提高热中子的探测效率和提高测量中子能量探测上限等方面［10-12］. 能量分辨率的进一步提高则存在较大困难，而且解谱的准确度受预制谱的影响较大. 尤其在硼中子俘获治疗（BNCT）领域——主要使用超热中子和含硼靶向药物用于肿瘤的定向治疗，超热中子能谱的准确探测对能谱仪提出了新的要求. 日本国家防卫大学的Takada等人［13］提出使用碳化硼（B4C）对中子进行慢化与吸收、利用LiF探测器进行中子计数测量的方法，能够较好地使各个探测器响应曲线的峰分开，使得探测器的分辨率有所提高，并显著提升了热中子和超热中子区域的探测效率，验证了该方法具有较大技术优势.

在中子能谱解析算法方面，国内外相关团队发展了类似SAND-Ⅱ算法、Gravel算法、遗传算法（GA）和极大似然算法（MLEM），以及基于神经网络的多种解谱算法，用于对中子能谱进行解析［14-17］，已较为成熟. 其中， Gravel算法由SAND-Ⅱ算法改进而来，是1996年由德国 PTB 实验室提出的一种交互式迭代算法. 它具有低噪声和解为非负等优点，自诞生以来在少道算法方面应用广泛，不仅可以对于多球谱仪的响应进行中子能谱解析［8，12，17］，而且对反冲质子法和活化法测量中子能谱［18，19］的解谱精度也很高. 该算法同样适用于γ能谱解析［20］. 中国辐射防护研究院的李建伟等人［21］利用MCNP模拟获得了几种辐射防护领域的常见中子能谱，而后使用迭代算法进行解谱研究. 其结果表明， 基于迭代法的解谱算法精度较高，但同时对预置谱精度的要求也较高. 而各种场景下的中子能谱可能非常复杂且具有显著差异，通常难以获得高精度的预置谱.这制约了解谱精度的进一步提升.

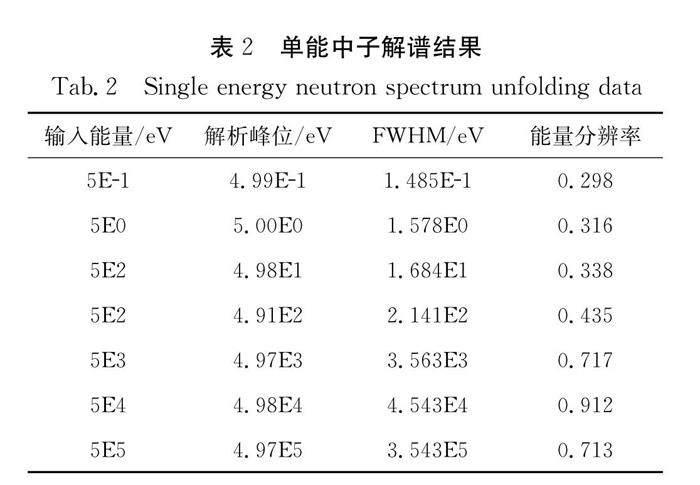
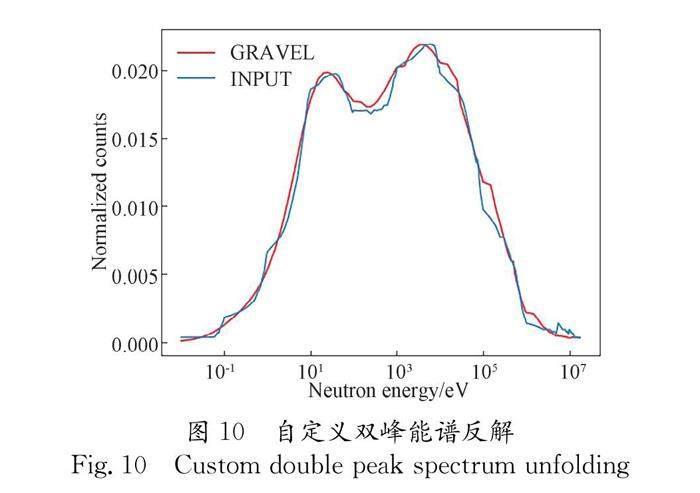
本文针对硼、锂元素的中子反应截面规律，提出了一种使用硼、锂作为慢化体和灵敏探测器的通用中子能谱仪设计方法，并使用碳化硼作为慢化体、涂硼微结构中子探测器作为灵敏体进行了设计验证. 该方法可实现各个灵敏中子探测器响应函数之间的解耦，在通用中子能谱设计上具有较大技术优势. 基于该方法，我们设计了一个用于BNCT超热中子能谱探测的中子能谱仪，用碳化硼作为慢化体，包括15个灵敏体探测器. 利用MCNP模拟我们获得了该能谱仪在各种中子输入下的探测器响应，验证了设计方法的准确性. 最后，本文提出了基于响应函数的预置谱设置方法，并利用Gravel算法实现了能谱解析，可反解得到相应的中子能谱. 我们用标准BNCT能谱进行了测试和验证［22］ ，结果表明该设计方法具有较好的适用性和技术优势.

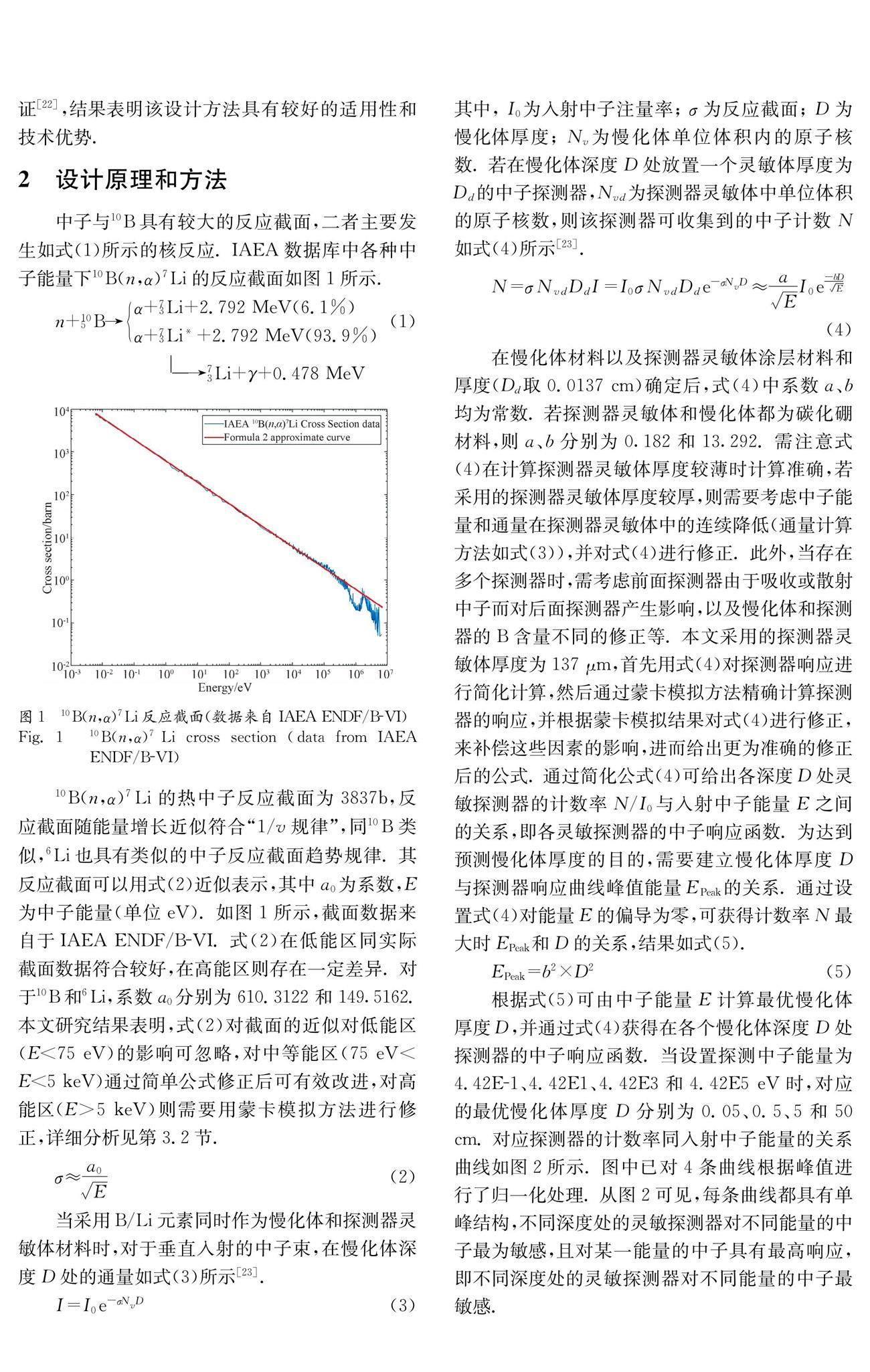
10B（n，α）7Li的热中子反应截面为3837b，反应截面随能量增长近似符合“1/v规律”，同10B类似，6Li也具有类似的中子反应截面趋势规律. 其反应截面可以用式（2）近似表示，其中a0为系数，E为中子能量（单位eV）. 如图1所示，截面数据来自于IAEA ENDF/B-VI. 式（2）在低能区同实际截面数据符合较好，在高能区则存在一定差异. 对于10B和6Li，系数a0分别为610.3122和149.5162.本文研究结果表明，式（2）对截面的近似对低能区（E＜75 eV）的影响可忽略，对中等能区（75 eV

σ≈a0 E（2）

当采用B/Li元素同时作为慢化体和探测器灵敏体材料时，对于垂直入射的中子束，在慢化体深度D处的通量如式（3）所示［23］.

I=I0e-σNvD（3）

其中， I0为入射中子注量率; σ为反应截面; D为慢化体厚度; Nv为慢化体单位体积内的原子核数. 若在慢化体深度D处放置一个灵敏体厚度为Dd的中子探测器，Nvd为探测器灵敏体中单位体积的原子核数，则该探测器可收集到的中子计数N如式（4）所示［23］.

N=σNv dDdI=I0σNv dDde-σNvD≈a EI0e-bD E（4）

在慢化体材料以及探测器灵敏体涂层材料和厚度（Dd 取0.0137 cm）确定后，式（4）中系数a、b均为常数. 若探测器灵敏体和慢化体都为碳化硼材料，则a、b分别为0.182和13.292. 需注意式（4）在计算探测器灵敏体厚度较薄时计算准确，若采用的探测器灵敏体厚度较厚，则需要考虑中子能量和通量在探测器灵敏体中的连续降低（通量计算方法如式（3）），并对式（4）进行修正. 此外，当存在多个探测器时，需考虑前面探测器由于吸收或散射中子而对后面探测器产生影响，以及慢化体和探测器的B含量不同的修正等. 本文采用的探测器灵敏体厚度为137 μm，首先用式（4）对探测器响应进行简化计算，然后通过蒙卡模拟方法精确计算探测器的响应，并根据蒙卡模拟结果对式（4）进行修正，来补偿这些因素的影响，进而给出更为准确的修正后的公式. 通过简化公式（4）可给出各深度D处灵敏探测器的计数率N/I0与入射中子能量E之间的关系，即各灵敏探测器的中子响应函数. 为达到预测慢化体厚度的目的，需要建立慢化体厚度D与探测器响应曲线峰值能量EPeak的关系. 通过设置式（4）对能量E的偏导为零，可获得计数率N最大时EPeak和D的关系，结果如式（5）.

EPeak=b2×D2（5）

根据式（5）可由中子能量E计算最优慢化体厚度D，并通过式（4）获得在各个慢化体深度D处探测器的中子响应函数. 当设置探测中子能量为4.42E-1、4.42E1、4.42E3和4.42E5 eV时，对应的最优慢化体厚度D分别为0.05、0.5、5和50 cm. 对应探测器的计数率同入射中子能量的关系曲线如图2所示. 图中已对4条曲线根据峰值进行了归一化处理. 从图2可见，每条曲线都具有单峰结构，不同深度处的灵敏探测器对不同能量的中子最为敏感，且对某一能量的中子具有最高响应，即不同深度处的灵敏探测器对不同能量的中子最敏感.

随后我们进一步研究了各响应曲线的峰位能量（EPeak）、慢化体厚度、峰值计数率、半高宽（FWHM）和相对宽度（FWHM/EPeak）随慢化体厚度的变化规律，结果如表1所示. 结果表明，随着慢化体厚度的增加，响应曲线的峰值计数率逐渐降低，峰位能量和半高宽都逐渐增加，相对宽度保持不变，约为18.45.

3 用于BNCT中子能谱测量的能谱仪

3.1 能谱仪设计

基于上述设计方法，针对BNCT超热中子能谱的测量需求，使用天然丰度的碳化硼作为慢化体，使用涂硼硅基微结构中子探测器设计了一个超热中子能谱仪，共包括15个灵敏探测器. 由于BNCT主要关注在0.1 eV～10 keV的超热能区，因此将15个探测器可测量的中子峰位能量设计为近似均匀分布在0.1 eV～10 keV范围内，并通过公式（5）获得了每个探测器对应的慢化体厚度，得到能谱仪的结构示意图如图3所示. 图中每个探测器对应的可测量中子峰值能量依次为：0.40、0.80、1.60、3.30、6.20、13.00、24.00、46.00、90.00、175.00、340.00、1300.00、2500.00、5000.00和10 000.00 eV. 在计算过程中，已考虑了前端探测器和慢化体对后端探测器响应的影响.

15个探测器的响应函数波形可通过式（4）计算，结果如图4a所示. 图中将所有区间的峰值进行了归一化以便于对比，每条响应曲线的峰值计数率和半高全宽（FWHM）值如图4b所示. 图中可见，15条响应曲线具有类似的形状，其峰值随慢化体厚度增大而逐渐增加，均匀分布在0.1 eV～10 keV范围内，达到了设计预期要求. 由于碳化硼具有较大的中子吸收截面，因此峰值计数率随慢化体厚度的增加而快速衰减. 同截面曲线类似，峰值计数率随能量按1/sqrt（E）规律变化，第1个探测器（峰位0.40 eV）的峰值计数率为0.121，而第15个探测器（峰位10 keV）的峰值计数率为6.91E-4，降低了约175倍. 响应曲线的FWHM随探测峰位的增大而增大，但相对宽度固定不变. 相对宽度为R=FWHM/E，其中FWHM为中心能量为E的探测器所对应响应函数的半高宽. 此处的相对宽度为中子谱仪对单能中子响应函数的半高宽除以峰值能量，是15个计数型探测器综合获得的结果，同模拟中的能谱展宽等因素无关. 同时相对宽度同中子谱仪的中子探测能量分辨率不同，虽然响应函数的相对宽度较大，但通过15个计数型探测器联合解谱，可显著提高最终的中子能量分辨率，具体见第4节. 3.2 蒙卡模拟验证

针对设计的能谱仪，通过MCNP模拟对响应函数进行了验证，检查设计方法的可行性. 此外，在能谱仪外围用厚度1 cm的聚乙烯进行包裹，以减弱周围环境中散射中子的干扰，结构如图3所示. 此部分包裹结构以及探测器材料与空气的影响难以通过公式直接计算，需要通过蒙卡模拟方法进行修正. 公式（4）中对于探测器计数的简化计算也可以通过蒙卡模拟的结果进行修正.

MNCP5采用美国国家核数据中心（NNDC）维护的ENDF/B-Ⅵ子截面数据库，针对B/Li截面，该数据库与IAEA推荐的截面数据相吻合. 使用MCNP程序的F4卡对15个灵敏探测器栅元的中子平均体通量进行统计，与FM4乘子卡结合来获得相应栅元内发生核反应的计数［24］. 为尽可能准确地模拟得到15个探测器的中子响应函数，采用能量为0.1 eV～20 MeV范围内共计177个单能中子束垂直入射能谱仪.每个能量点模拟1E9个事例，相对误差大多低于0.1%，仅在低能中子入射时会导致个别位于中子射程截止处的探测器误差较大，约为1%～10%. 利用FM4卡进行计数，得到15个中子响应函数结果如图5a所示，图中已对峰值计数率进行了归一化处理以便于对比.在低能区时，响应函数同式（4）给出的曲线形状较为一致，但高能区的差异则较大，这是由于反应截面在高能区存在多个峰结构（见图1），导致高能区探测器的响应曲线存在多个峰结构. 各区间的峰值计数率和FWHM如图5b所示，峰值计数率与能量近似按1/sqrt（E）规律变化. 对比图4b可以得到，在低能区（小于100 eV）峰值计数率和FWHM与计算值符合得较好；在中高能区（100 eV～0.1 MeV）峰值计数率逐渐偏低，FWHM逐渐变宽；在0.1 MeV左右时，由于截面吸收峰的影响导致FWHM变窄. MCNP模拟结果与式（4）和式（5）计算得到的峰值计数率和FWHM之间的平均偏差约为26.7%和57.8%，结果与预期偏差较大，详细分析如下.

图6中展示了公式（4）计算得到的相对宽度与MCNP模拟得到的相对宽度曲线.相对宽度R=FWHM/E，其中FWHM为中心能量为E的探测器所对应响应函数的半高宽. 二者在低能区基本一致;在中能区模拟结果则远大于计算结果，表明式（4）对反应截面的近似较大低估了相对宽度；而在高能区相对宽度又迅速降低，此为模拟的半高宽在高能端趋于稳定所致（见图5b）. 说明截面公式对于高能区的近似以及能谱仪外增加的1 cm包裹层的贡献，即公式（4）更适用于75 eV以下能区的计算. 在高能时响应函数展宽较大.如对于峰值能量为90 eV的探测器，其响应曲线中峰值高度一半对应的能量分别为8.25 eV和5200 eV. 因此，虽然公式（2）在100 keV以下都可较好地描述截面，但响应曲线对应半高宽的误差依然较大. 由于误差随慢化体厚度的增加而增大，导致二者偏差随慢化体厚度增加而增大. 图6中在高能时二者趋于接近，是由于高能区下的响应曲线从单峰结果演化为多峰结果，导致FWHM计算出现偏差所致. 为了更准确地描述响应曲线，在中高能区需用蒙卡模拟结果进行修正，修正方法和结果见下一节.

3.3 探测器响应曲线修正与拟合

对比图4和图5的响应曲线，可以发现二者在低能区可较好符合，在中高能区则存在显著差异.因此需要用蒙卡模拟结果对式（4）和式（5）进行修正，提高计算得到响应曲线的准确性.

计算设定的15个探测器的实际峰位能量和MCNP模拟计算得到的实际峰位能量结果如图7所示. 图中可见，二者结果在低能区较为一致，在高能区时式（5）高估了所需的慢化体厚度.这是由于式（2）的截面公式高估了高能区的中子截面. 通过拟合MCNP结果可获得修正后的中子能量和慢化体厚度的计算公式，使之更适合用于中子能谱仪的设计. 为更好拟合MCNP模拟结果，对图7数据进行分段拟合.拟合公式如式（6）所示. 拟合相关系数R2值为0.9999和0.9998，表明拟合效果较好. 基于式（6），可根据设定的探测器峰位能量来实现对慢化体厚度的快速设计.

EPeak=207.670D2.649+0.100，D<0.714 cm

265.852D3.529+4.206，D≥0.714 cm（6）

由于模拟和计算的响应曲线间存在一定差异，需要对公式（4）进行修正.同样的，仅需要对中高能区结果进行修正. 在能量E低于75 eV时，不需要进行修正；在能量E高于75 eV时，需要进行修正. 修正方法为：在公式（4）的基础上增加一个高斯函数，高斯函数的系数为p， 平均值位于0.01 MeV， 标准差为1 MeV. 针对不同慢化体厚度D，修正参数有2个，分别为系数m，p. 修正后的响应函数计算方法如式（7）所示，修正系数m， p以及4个典型响应函数如图8所示.

N=0.182 Ee-13.292D E，E≤75 eVm*0.182 Ee-13.292D E+Gauss（p，1E4，1E6），

E>75 eV（7）

图8c～8f展示了其中4个探测器进行修正后的响应函数和MCNP模拟结果的对比图.对于能量低于75 eV的部分未进行修正；能量高于75 eV的部分在修正后，蒙卡模拟数据同式（7）拟合结果更为一致. 对于峰位能量在75 eV以下的探测器，拟合R2值均在0.95以上；峰位能量在75～5000 eV之间的探测器，拟合R2值从不修正时的低于0.9，提高到修正后的0.95以上；而峰位能量高于5 keV的探测器在修正后拟合效果依然较差，但拟合R2值仍较修正前有所提高.

图8 （a， b）拟合参数m、p拟合曲线;（c～f）探测器响应曲线拟合举例

Fig.8 （a， b） Fitting curves of parameters m and p; （c～f） examples of detector response curve fitting

式（7）中设置75 eV的截断是为了消除叠加的高斯函数修正项在低能端的贡献. 在不加截断时，高斯修正项将导致低能端曲线异常偏高.通过设置75 eV的截断可降低其对低能端曲线的影响，有助于改善拟合效果.但该截断将导致修正项在75 eV处不连续. 对于低能区探测器，式（7）中针对第一项的修正系数m可补偿该截断的影响，使截断可忽略不计. 但对于高能区探测器，式（7）的第一项修正无法补偿该截断的影响，导致在75 eV存在明显的截断，使修正效果较差. 即式（7）更适合用于计算低能区（5 keV以下）探测器的响应函数，对于高能区探测器则存在误差，需要借助蒙卡模拟程序来提高精度.

图8a和图8b展示了15个探测器修正参数m、p的数值，并对修正系数数据进行了拟合，拟合公式见式8. 两个修正参数均可用幂函数进行拟合，拟合的R2值分别为0.9100和0.8977.

m=11.32E0.45-2.8p=0.000202E-0.123（8）

综上，可根据公式（6）（7）（8）进行中子能谱仪的快速设计. 通过设定探测器可探测的能量中心值，利用公式（6）获得其对应的慢化体厚度，利用公式（7）（8）获得其响应函数. 基于该方法可实现对中子能谱仪的快速初步设计，可快速获得一个接近最优方案的探测器结构，有效避免需要大量蒙卡模拟计算才可进行中子能谱仪设计的缺点. 但该方法给出的响应函数存在一定的误差，适合用于低能区探测器的响应函数计算，尤其是中心能量在5 keV以下的探测器响应函数计算.在计算高能区探测器的响应函数时则存在一定的误差，需通过蒙卡方法进行修正. 由于本文设计的中子能谱仪针对BNCT超热中子，不关注快中子能区，因此是否对5 keV以上能区探测器响应矩阵进行修正并不影响超热中子能区的解谱结果. 研究结果表明，在直接使用公式（7）（8）计算的响应函数且不用蒙卡结果进行修正时，在超热中子能区，二者解谱结果没有差异.

4 中子能谱解析

在获得探测器阵列的响应矩阵R后，针对探测器阵列的输出计数率向量N，可解谱得到入射中子能谱φ，三者关系可以用式（9）表示［25］.

N1N2Nn=R11R12…R1mR21R12…R2mRn1Rn2…Rnm×φ1φ2φm （9）

式（9）中N的每一行为单个探测器的输出计数率，计算方法见式（10）.

Ni=∑mk=1Rikφk i=1，2，…，n.（10）

其中，n为能谱仪中探测器的数量; m为待求解能谱的分区数量. 解谱过程是针对每一组探测器计数率输出向量N，通过响应矩阵R求解入射中子能谱φ的过程.

对于本文设计的BNCT能谱仪，其响应矩阵可通过修正后的公式（7）获得，并对5 keV以上的高能区探测器使用蒙卡模拟得到的响应函数进行代替. 其中n=15，m=177，表示通过15个中子探测器进行能谱测量和解析，可获得0.1 eV～20 MeV能量范围内共计177个能量区间内的中子强度. 因此，响应矩阵R为15×177的矩阵.

由于各探测器响应函数的峰值计数率存在显著差异，尤其是高能端探测器的峰值计数率较低，导致其响应灵敏度较差，从而可能较大延长能谱探测所需要的时间. 提高高能端探测器的响应灵敏度，缩短能谱探测所需要的时间，可通过提高高能端探测器的权重来解决. 本文将探测器权重设置为各探测器响应函数峰值的倒数，将各个探测器的响应灵敏度调整为基本一致. 将修正后的响应函数同时用于能谱探测和能谱解析，则对解谱结果无影响.

响应矩阵R通常存在n<

φ（k+1）j=φ（k）jexp ∑ni=1Wkijln Ni∑ml=1Rilφkl∑ni=1Wkij ， i=1， 2，…， n；j=1， 2，…， m（11）

其中，φj为第j个能区的迭代能谱注量率；Ni为第i个探测器的实测计数率；W称作权重因子，其计算公式见式（12）［26］.

W（k）ij=NiRijφkj∑ml=1Rilφkl（12）

Gravel的收敛条件如式（13）～（15）所示.

J（k）=∑ni=1（Ni-qki）2∑ni=1qki（13）

J（k+1）=J（k）-J（k+1）（14）

ΔJ（k+1）=J（k）-J（k+1）（15）

当ΔJ（k+1）小于某一自定义的值时，即判断为收敛. 其中，式（13）中q（k）i的计算公式如式（16）所示.

q（k）i=∑mj=1Rijφ（k）j（16）

对于类似Gravel之类的迭代算法，迭代精度受预置谱影响较大，而在实际应用中的大多数情况下很难得到较为准确的预置谱. 因此，本文将探测器输出计数率向量N（1×n）与探测器阵列响应矩阵的转置RT（n×m）点乘得到对应预置谱φ0（1×m） ，如式（17）所示. 结果表明，由于能谱仪各探测器的响应函数实现了解耦，通过该方法设置的预置谱具有良好的普适性，可用于各种类型中子能谱的解析. 主要原因是各探测器的响应函数之间实现了基本解耦.

φ0=N×RT （17）

4.1 单能中子能量解谱

通过蒙卡模拟获得了能谱仪对单能中子输入时的响应情况，输入单能中子能量分别为5E-1、5E0、5E1、5E2、5E3、5E4和5E5 eV，基本覆盖了所有热中子、超热中子和快中子能区. 用MCNP计算得到能谱仪的15个探测器在各种单能中子输入时的输出计数率向量，输入Gravel算法进行能谱解析，结果如图9所示. 本文所有解谱输出均为Gravel算法的直接输出结果，未进行进一步处理，设置Gravel算法收敛条件为两次迭代间的相对偏差小于1E-10.

解谱得到的单能中子峰与输入谱的峰位一致程度较好，峰位偏差小于1%. 随着输入单能中子能量的增加，解谱带来的展宽逐渐增加，即相对分辨率逐渐变差，从低能端的约30%逐渐增加到高能端的约90%. 在0.5 MeV单能中子输入时，解谱结果中出现了两个峰.在0.5 MeV的真实中子峰左侧，出现了峰位在0.23 MeV的假峰. 其原因是此处响应函数存在多个峰结构，如图5所示，尤其是对此能区中子最为灵敏的几个探测器的响应函数都存在假峰，导致能谱解析时出现假峰. 将最敏感的最后两个探测器的响应函数进行平滑处理，再利用平滑后的响应函数进行解谱，可以避免产生此假峰. 确认假峰的出现是响应函数中的多峰结构所致，解谱结果如图9所示. 解谱中使用探测器响应灵敏度一致的响应矩阵，可有助于提高解谱效率和准确度. 解析得到能谱的峰位、半高宽和能量分辨率如表2所示.

4.2 连续中子能谱解谱

设置了一个拥有复杂双峰结构的中子能谱作为输入， 通过响应矩阵快速获得中子能谱仪的输出向量，用Gravel算法进行能谱解析，来验证解谱算法精度，输入能谱和解谱能谱结果如图10所示.

由图10可得，反解能谱与输入双峰能谱符合程度较好，两个能峰的峰位基本重合，但受探测器分辨率的限制，导致双峰之间波谷部分的符合程度较差，同时在高能端细节结构上存在一定误差. 为了准确评价解谱的精确程度，分别利用输入能谱与解析能谱之间的均方差值（MSE）表征解析谱和真实中子谱之间的差异程度， 用平均相对偏差值（ARD）表示解析谱与真实中子能谱之间的偏差程度，用中子能谱质量值（Qs）表示解析谱与真实中子谱的接近程度.理想状态下上述三个指标应接近于0［8］. 图10中的MSE为0.896%、ARD为7.54%、Qs为7.35%，表明解谱符合程度较好，从而验证算法的可行性.

为反解得到BNCT能谱，采用中国科学院上海应用物理研究所的朱益楠等人［22］基于氘氚中子源经BSA慢化整形后的BNCT中子能谱作为MCNP的输入. 该中子能谱符合IAEA推荐的BNCT治疗用中子束指标［27］. 模拟获得了能谱仪探测器阵列的输出计数率向量，通过GRAVEL算法进行解谱，结果如图11所示.

图中可见，GRAVEL算法给出的能谱和输入能谱符合较好，可较好的重现BNCT能谱结构. 仅在0.1～20 MeV的高能范围内存在差异，原因是该能谱仪的15个中子探测器均是针对超热中子能区的，对快中子响应灵敏度较差，限制了在该区域的灵敏度. 此外，10B（n，α）7Li反应截面在该范围内存在多个峰结构，也导致解析难度的增加. 增加一个对快中子响应敏感的探测器可有效提高在快中子能区的测量精度. 由于BNCT能谱主要位于超热中子能区，快中子影响相对较小，因此本文设计的能谱仪主要采用对超热中子能区敏感的探测器，其体积更小，具有便携性和较好的灵敏度.

图11中的MSE为0.76%、ARD为8.11%、Qs为6.67%，说明解谱的精度较高. 结果表明，GRAVEL算法反解得到的中子能谱与输入谱符合度较高，说明该能谱仪适用于BNCT的能谱测量和解析. 对比中国原子能科学研究院的陈军等人［28］利用多球谱仪求解的BNCT能谱，本文的中子能谱仪反解得到的能谱精度更高，峰的展宽更小，从而验证了本结构的优越性.

5 结 论

本文提出了一种使用B/Li作为慢化体和灵敏探测器的通用中子能谱仪快速设计方法.此方法可通过公式快速实现能谱仪最优慢化体厚度和中子探测器响应函数的计算， 结果同蒙特卡罗模拟结果较为一致. 该类能谱仪各个探测器的响应函数可实现解耦，在预置谱设置、解谱精度等方面具有较大的优势. 利用B4C作为中子探测器的慢化吸收体，设计了一个针对BNCT超热中子探测的能谱仪，利用少道解谱算法GRAVEL算法实现了能谱解析. 解谱结果表明， 该能谱仪具有较高的中子能谱测量精度，可以用于BNCT超热中子的能谱探测，验证了该方法的可行性.

参考文献：

［1］ 蒋世伦， 祁建敏， 王立宗， 等. 反冲质子磁分析技术用于氘氚中子能谱测量研究［J］. 物理学报，2011， 61： 072902.

［2］ 祁建敏， 周林， 蒋世伦， 等.聚变中子能谱测量系统脉冲中子灵敏度的实验研究［J］. 物理学报， 2013，62： 245203.

［3］ 陈永浩. 反冲质子法快中子能谱测量及解谱技术研究［D］. 兰州： 兰州大学， 2013.

［4］ Esposito A， Bedogni R， Domingo C， et al. Measurements of leakage neutron spectra from a high-energy accumulation ring using extended range bonner sphere spectrometers ［J］. Radiat Meas， 2010， 45： 1522.

［5］ Goldhagen P， Reginatto M， Kniss T， et al. Measurement of the energy spectrum of cosmic-ray induced neutrons aboard an ER-2 high-altitude airplane ［J］. Nucl Instrum Meth A， 2002， 476： 42.

［6］ Vega-Carrillo H R， Manzanares-Acua E. Background neutron spectrum at 2420 m above sea level ［J］. Nucl Instrum Meth A， 2004， 524： 146.

［7］ Wiegel B， Agosteo S， Bedogni R， et al. Intercomparison of radiation protection devices in a high-energy stray neutron field， Part II： bonner sphere spectrometry ［J］. Radiat Meas， 2009， 44： 660.

［8］ 程凯， 魏鑫， 曾德凯， 等. 基于微结构气体探测器对单能和连续谱快中子的模拟解谱［J］.物理学报， 2021， 70： 112901.

［9］ 邹益晟， 肖德涛， 张伟华， 等. 基于单球中子谱仪的能量响应模拟及解谱方法研究［J］.辐射防护， 2019， 39：  280.

［10］ Birattari C， Esposito A， Ferrari A， et al. Calibration of the neutron rem counter LINUS in the energy range from thermal to 19 MeV ［J］. Nucl Instrum Meth A， 1993， 324： 232.

［11］ Birattari C， Ferrari A， Nuccetelli C， et al. An extended range neutron rem counter ［J］. Nucl Instrum Meth A， 1990， 29： 250.

［12］ Tolymkhan Y， 王忠海， 陈秀莲， 等. 以水作为慢化体的多球中子谱仪模拟与解谱研究［J］. 四川大学学报： 自然科学版， 2020， 57： 735.

［13］ Takada M， Abe Y， Nakamura S， et al. Spectrometer design of low energy neutrons for boron neutron capture therapy ［J］. Nucl Instrum Meth A， 2021， 1020： 165848.

［14］ Hosseini S A， Alvarez-Galvan M C. Study of physical-chemical properties and catalytic activities of ZnCr2O4 spinel nano oxides obtained from different methods—modeling the synthesis process by response surface methodology and optimization by genetic algorithm ［J］. J Taiwan Inst Chem E， 2016， 61： 261.

［15］ 莫双荣， 刘钰， 幸浩洋， 等. Elman 神经网络在中子解谱中的应用［J］. 四川大学学报： 自然科学版，2020， 57： 531.

［16］ Pehlivanovic B， Avdic S， Marinkovic P， et al. Comparison of unfolding approaches for monoenergetic and continuous fast-neutron energy spectra ［J］. Radiat Meas， 2013， 49： 109.

［17］ 王松林， 王琦， 徐小三， 等. 阈探测器法测量 Am-Be 中子源屏蔽辐照腔内的中子能谱 ［J］. 原子能科学技术， 2009， 43： 16.

［18］ Suman V， Tripathy S P， Sunil C， et al. Measurement of neutron energy distributions from p+Be reaction at 20 MeV using threshold activation foils ［J］. IEEE T Nucl Sci， 2016， 63： 2283.

［19］ Wang G Y， Han R， Liu J L. Comparison and research on the GRAVEL and PRIP algorithms of neutron energy spectrum unfolding ［J］. Radiat Detect Techno， 2017， 1： 5.

［20］ 张驰， 王玉东， 周荣， 等. G（E）法与Gravel法处理能谱剂量转换效果研究［J］. 核电子学与探测技术，2017， 37： 268.

［21］ 李建伟， 李德源， 刘建忠， 等. 三种解谱算法求解中子能谱的解谱效果比较［J］. 核电子学与探测技术， 2017， 37： 147.

［22］ 朱益楠，林作康，卢林远，等. 基于氘氚中子源硼中子俘获治疗的中子慢化整形研究［J］.核技术， 2022， 45： 010202.

［23］ 卢希庭. 原子核物理（修订版）［M］. 北京：原子能出版社， 2000： 242.

［24］ 燕奕宏， 谭新建， 翁秀峰， 等. 三氟化硼Bonner多球谱仪的中子源能谱测量方法［J］. 西安交通大学学报， 2020， 54： 136.

［25］ Banerjee K， Ghosh T K， Kundu S， et al. Variation of neutron detection characteristics with a dimension of BC501A neutron detector ［J］. Nucl Instrum Meth A， 2009， 608： 440.

［26］ Liu B， Lv H， Li L， et al. Study on iterative regularization method and application to neutron spectrum unfolding of multi-sphere spectrometer measurement ［J］. Nucl Instrum Meth A， 2021， 992： 165027.

［27］ Levin V A P， Dodd B. Current status of neutron capture therapy ［R］. Vienna， Austria： IAEA， 2001.

［28］ 陈军， 李春娟， 李玮， 等. 多球谱仪测量BNCT医院中子照射器中子束能谱［J］. 原子能科学技术，2014， 48： 2127.

引用本文格式：