一种基于SwinTransformer神经网络的低截获概率雷达信号调制类型的识别方法
2023-04-29董章华赵士杰赖莉
董章华 赵士杰 赖莉


本文针对低截获概率(Low Probability of Intercept, LPI)雷达信号调制类型的识别问题提出了一种基于Swin Transformer神经网络的识别方法. 该方法首先用平滑伪Wigner-Ville分布对信号进行时频变换,将一维时域信号转换为二维时频图像,然后使用Swin Transformer神经网络对时频图像进行特征提取和调制类型识别. 仿真结果显示该方法具有较强的抗噪声能力,在低信噪比条件下识别准确率高,且具有较强的小样本适应能力.
低截获概率雷达; Swin Transformer神经网络; 平滑伪Wigner-Ville分布; 调制类型识别
O29A2023.021004
收稿日期: 2022-05-11
基金项目: 国家重点研发计划(2020YFA0714000)
作者简介: 董章华(1996-), 男, 四川成都人, 硕士研究生, 主要研究方向为智能系统和数学信息技术. E-mail: mathpix01@163.com
通讯作者: 赖莉. laili@scu.edu.cn
A radar signal modulation type recognition method based on Swin Transformer neural network
DONG Zhang-Hua, ZHAO Shi-Jie, LAI Li
(School of Mathematics, Sichuan University, Chengdu 610064, China)
In this paper, based on the Swin Transformer neural network we propose a method for the recognition of modulation type of Low Probability of Intercept (LPI) radar signal. We firstly perform the time-frequency transformation, say, transform the one-dimensional time-domain radar signal into a two-dimensional time-frequency image by using the smooth pseudo Wigner-Ville Distribution (WVD). We then use the Swin Transformer network to extract the desired feature from the image and identify the modulation type. Numerical simulation shows that this method possesses strong anti-noise ability and high recognition accuracy even under the condition of low signal-to-noise ratio. Meanwhile, it is also shown that this method has strong adaptability to small samples.
LPI radar; Swin Transformer neural network; Smooth pseudo WVD; Radar signal modulation type recognition
1 引 言
近年来,随着低截获概率(Low Probability of Intercept, LPI)雷达技术的发展,传统的雷达辐射源识别方法的识别准确率大大降低. 鉴于LPI雷达辐射源的有效识别基于雷达信号的调制类型的识别,如何提高LPI雷达信号的调制类型的识别率就成为提高对于LPI雷达的侦察能力的关键问题. 对此问题,国内外学者开展了大量研究,取得了丰硕成果, 如张等提出的基于熵特征和信息维数等的调制类型识别算法[1-3]及文献[4-9]基于时频分析方法进行的信号调制类型的识别,等. 在中等信噪比条件下(高于4 dB),这些算法有较好的识别效果. 同时,在信噪比高于0 dB的条件下,这些算法也能在小样本(训练集大小为200)条件下取得较好的识别效果.
近年来,随着深度学习方法在图像处理中的广泛应用, 将时频变换后获得的LPI雷达时频图像(Time-Frequency Image,TFI)与深度学习算法相结合的研究成果越来越多. 例如,基于卷积神经网络(CNN)的深层次自动特征提取能力[10],文献[11]将其应用于信号的时频图像,在信噪比为-2 dB时识别率接近94%. 文献[12]将去噪后的雷达信号的时频图像输入Alex Net卷积神经网络进行调制类型识别,在信噪比为-6 dB时识别率达到90%以上. 文献[13]则提出了一种基于Choi-Williams分布(CWD)和深度卷积神经网络迁移学习的调制类型识别方法. 此外,文献[14]通过两个独立网络(卷积神经网络(CNN)和Elman神经网络(ENN))来处理时频图像的特征提取问题. 文献[15]通过卷积神经网络完成去噪,用Inception-V4网络进行特征提取,在数据量为200时识别率接近90%,未去噪时识别率则约为75%. 文献[16]评估了AlexNet和GoogleNet在不同数据集上的识别精度. 文献[17]采用ResNet解决了CNN中梯度消失的问题. 文献[18]提出了一种基于CNN的分层调制类型分类器,其中的两个CNN分别基于低阶特征和高阶特征进行识别. 以上这些方法多基于卷积神经网络,需要对雷达时频图像进行较为繁琐的预处理. 在低信噪比条件下,这些方法必须进行去噪预处理,效率低、识别率不高.
不同于常见的卷积神经网络,本文将时频分析与深度学习相结合,用一种基于Swim Transformer的神经网络来提取时频图像的特征,然后用Softmax分类器来完成LPI雷达信号调制类型的识别. 对5种LPI雷达信号调制类型(BFSK、BPSK、Costas、LFM、QPSK)的仿真识别结果显示,在不同噪声条件、不同训练集大小条件下,该方法都具有较强的抗噪声能力和小样本适应性.
2 雷达信号转换
雷达信号x(t)=Aejφ(t)+n(t)是一种非平稳信号.单一的时域分析或频率分析并不能有效表征信号频率的时间变化.这里的n(t)为噪声. 另一方面,时频联合分析方法作为处理非平稳信号的基本方法, 可以直观地刻画信号的时域与频域的联合特征.典型的非线性时频分析方法主要有Wigner-Ville分布,Cohen类分布,Affine类分布等. 其中,Wigner-Ville分布(WVD)是信号瞬时自相关函数的傅立叶变换,具有许多优良性能,如对称性、时移性、组合性、复共轭关系等,且不会损失信号的幅值与相位信息,对瞬时频率和群延时敏感.
尽管WVD在信号可视化和波形识别[19]等领域有诸多应用, 但其抑制交叉项干扰的效果却较差. 为解决这个问题,我们引入如下的平滑伪Wigner-Ville分布.
SPWx(t,v)=∫+∞-∞∫+∞-∞x(t-u+τ/2)x*·
(t+u-τ/2)g(u)h(τ)e-j2πvtdτdu(1)
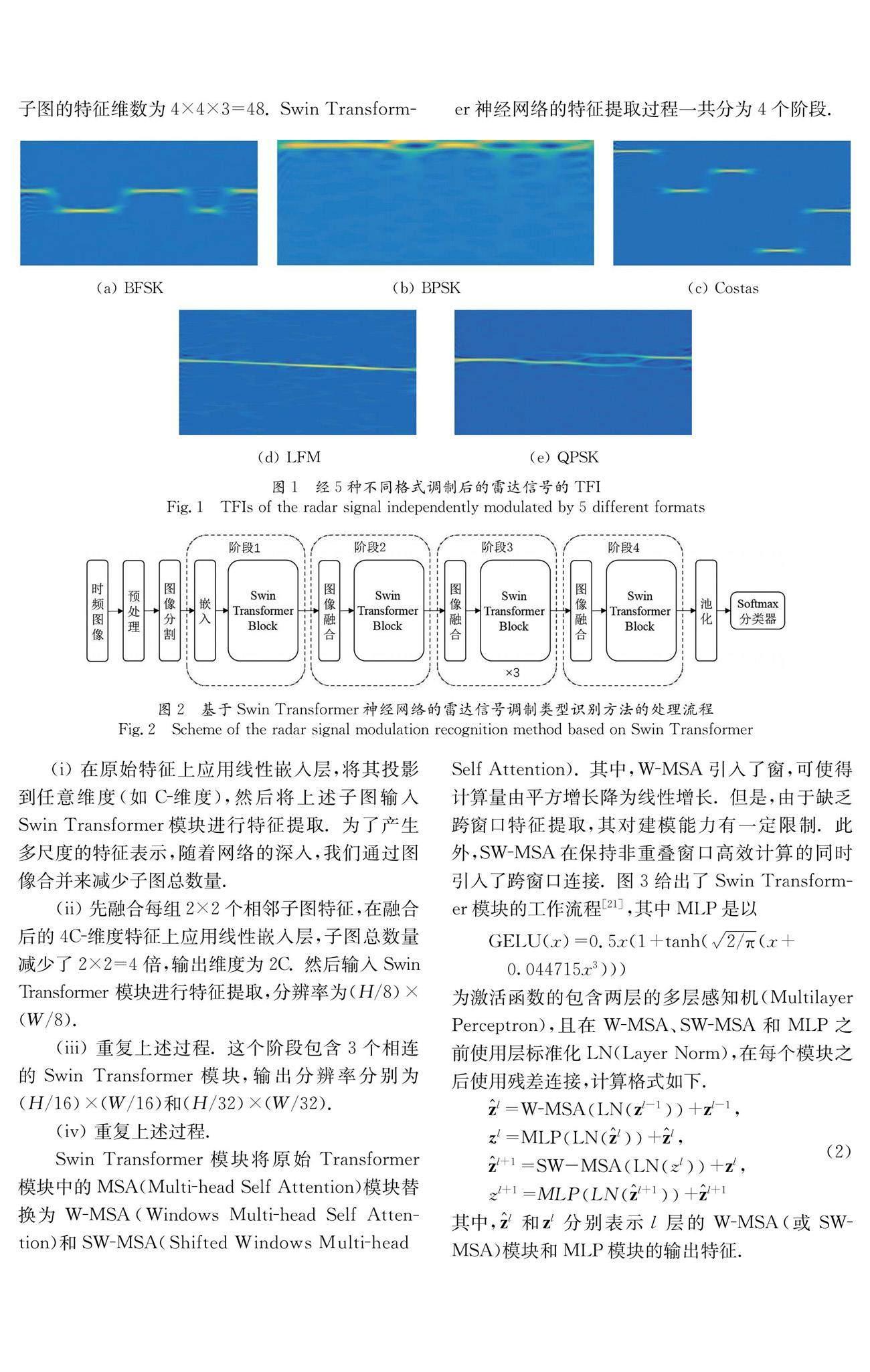
其中,g(u),h(τ)为窗函数,用于分别实现时域和频域的平滑滤波. 图1给出了分别经BFSK、BPSK、Costas、LFM和QPSK这5种调制方式处理之后的雷达信号经平滑伪Wigner-Ville分布变换后得到的TFI图像. 可以看到,经过平滑伪Wigner-Ville分布变换,TFI图像展示了信号调制周期与带宽特征. 后续我们将通过对TFI图像的特征提取来识别雷达信号的调制类型.
3 基于Swin Transformer神经网络的雷达信号调制类型识别
基于注意力机制的Transformer方法是自然语言处理领域的主流[20]. 在图像处理领域,Transformer方法可以通过注意力机制来捕获全局信息,对目标建立远距离依赖,进而提取出更强有力的特征. 进一步,Swin Transformer神经网络结合了CNN的层次化结构和Transformer模型的注意力机制优势[21],可以更好地识别雷达信号的调制类型. 图2给出了基于Swin Transformer神经网络的信号调制类型识别方法. 该方法主要由4个部分构成:图像预处理与分割,Swin Transformer模块,池化层及Softmax分类器.
首先,我们通过图像分割模块将输入的时频图像(宽度为W,高度为H)分割为非重叠的小尺寸子图,其特征被设置为原始时频图像像素RGB值. 在Swin Transformer中,我们使用4×4的子图大小,原始图像分割为(H/4)×(W/4)个子图,每个子图的特征维数为4×4×3=48. Swin Transformer神经网络的特征提取过程一共分为4个阶段.
(i) 在原始特征上应用线性嵌入层,将其投影到任意维度(如C-维度),然后将上述子图输入Swin Transformer模块进行特征提取. 为了产生多尺度的特征表示,随着网络的深入,我们通过图像合并来减少子图总数量.
(ii) 先融合每组2×2个相邻子图特征,在融合后的4C-维度特征上应用线性嵌入层,子图总数量减少了2×2=4倍,输出维度为2C. 然后输入Swin Transformer模块进行特征提取,分辨率为(H/8)×(W/8).
(iii) 重复上述过程. 这个阶段包含3个相连的Swin Transformer模块,输出分辨率分别为(H/16)×(W/16)和(H/32)×(W/32).
(iv) 重复上述过程.
Swin Transformer模块将原始Transformer模块中的MSA(Multi-head Self Attention)模块替换为W-MSA(Windows Multi-head Self Attention)和SW-MSA(Shifted Windows Multi-head Self Attention). 其中,W-MSA引入了窗,可使得计算量由平方增长降为线性增长. 但是,由于缺乏跨窗口特征提取,其对建模能力有一定限制. 此外,SW-MSA在保持非重叠窗口高效计算的同时引入了跨窗口连接. 图3给出了Swin Transformer模块的工作流程[21],其中MLP是以
GELU(x)=0.5x(1+tanh(2/π(x+ 0.044715x3)))
为激活函数的包含两层的多层感知机(Multilayer Perceptron),且在W-MSA、SW-MSA和MLP之前使用层标准化LN(Layer Norm),在每个模块之后使用残差连接,计算格式如下.
l=W-MSALNzl-1+zl-1,zl=MLPLNl+l,l+1=SW-MSALNzl+zl,zl+1=MLPLNl+1+l+1 (2)
其中,l和zl分别表示l层的W-MSA(或SW-MSA)模块和MLP模块的输出特征.
图4给出了W-MSA和SW-MSA工作原理[21]. 如图4a所示,在第l层,W-MSA从左上角像素开始进行常规窗口分割,将8×8特征图均匀地分割为大小为4×4(M=4)的2×2个窗口,并在每个窗口应用注意力机制. 在接下来的第l+1层,W-MSA则改变窗口分割方式,如图4b所示. SW-MSA按图4c所示方法置换(M/2,M/2)像素生成新的特征图,再将置换过的8×8特征图均匀地分割为大小为4×4(M=4)的2×2个窗口,并在新窗口应用注意力机制. 通过窗口的置换与重新分割,SW-MSA在保持非重叠窗口高效计算的同时引入了跨窗口连接.
在经过4个阶段的Swin Transformer模块的计算后,我们在输出特征上使用全局平均池化层,最后使用Softmax分类器实现雷达信号调制方式分类.
4 仿真与分析
4.1 数据集生成
针对前述5种调制方式,我们将信号参数的采用范围随机化,具体参数值如表1所示. 我们在雷达信号中加入高斯白噪声,在-12~8 dB的信噪比范围内以2 dB为步长,每一信噪比、每一调制方式生成600组数据(共计33 000组数据),其中80%用于训练,20%用于测试.
4.2 识别效果分析
为了验证Swin Transformer识别方法的有效性,我们将其与KNN、SVM、朴素贝叶斯和决策树等4种算法的识别结果进行比较. KNN可解释性强,不需要训练模型,可以直接使用数据进行分类,但预测速度慢、准确性差. 朴素贝叶斯同样可解释性强,可以高效处理高维数据,但其缺点是可能忽略雷达信号特征间的依赖关系. 决策树可读性强、
训练速度快,但易出现过拟合问题. SVM的训练速度快、泛化错误率低,但对参数和核函数的敏感性强. SVM和决策树都是具有坚实理论基础且具有较好鲁棒性的算法,因此具有较高的可比性.
混淆矩阵常用于在机器学习中总结分类模型预测结果. 我们以矩阵形式将数据集中的记录按照真实类别与分类模型预测类别判断这两个标准进行汇总. 图5展示了信号在信噪比为-10 dB时采用Swin Transformer神经网络的识别混淆矩阵及其他4种机器学习算法的识别混淆矩阵(图中识别准确率均保留两位小数). 其中,矩阵的行表示真实标签,列表示预测标签,矩阵的元素则表示对应真实标签的各预测标签所占比例,对角线上的值即为识别准确率. 可以看到,针对5种LPI雷达信号调制类型,使用Swin Transformer进行特征提取并分类的效果均明显优于其他4种算法. 例如,从图5a可以看到,Swin Transformer神经网络对BFSK、BPSK、Costas、QPSK 这4种调制类型识别准确率不低于93%,对LFM虽有一定的识别错误概率,但仍明显优于其它4种识别算法,在-10 dB信噪比下整体识别率可以达到90%以上.
4.3 抗噪声效果分析
图6展示了5种识别方法在不同信噪比下对5种LPI雷达信号调制类型的识别准确率. 可以看到,基于Swin Transformer方法在信噪比较低时仍有较为理想的识别准确率,整体上优于其他4种方法. 值得注意的是,不同的信噪比也会对结果产生影响,如LFM信号当信噪比较低时(-12 dB,-10 dB)Swin Transformer方法和其他4个识别算法一样准确率较低. 但是,随着信噪比的提高,前者的识别准确率快速提升. 在信噪比为-8~2 dB范围内,其识别的准确率显著高于其他4种方法.
4.4 鲁棒性分析
为了进一步验证不同识别方法的鲁棒性,我们选择信噪比为-10 dB的样本进行测试,训练集数量分别为200,400,600. 图7给出了5种方法在不同训练集大小下的识别准确率. 可以看到,随数据量的增加,所有方法的识别率都呈上升趋势,而Swin Transformer神经网络方法在不同数据量下的识别率均为最优,说明该方法对小样本具有较强的适应性. 当训练集每类数据量仅为200时,Swin Transformer方法的识别率约为83.5%,而当训练集大小为600时,其识别率则增至92.8%.
5 结 论
本文针对低截获概率雷达信号调制类型的识别问题提出一种基于Swin Transformer神经网络的识别方法. 该方法采用平滑伪Wigner-Ville分布对信号进行时频变换,得到一个二维时频图像,然后通过Swin Transformer神经网络对时频图像进行特征提取,最后再通过Softmax分类器实现调制类型识别. 通过仿真实验,我们对比分析了该方法与其它4种常见算法的识别率差异. 结果显示,基于Swin Transformer神经网络的识别方法具有较强的抗噪声能力,在低信噪比条件下对5种雷达信号(BFSK、BPSK、Costas、LFM、QPSK)有整体上不低于90%的识别准确率. 此外,该方法还具有较强的小样本适应能力,在训练样本数量较少的情况下仍可实现较高的识别准确率.
本文提出的方法有效地实现了LPI雷达信号的调制类型的识别,可以为有效检测、跟踪和定位雷达信号源提供基础,因而具有重要的潜在应用价值.
参考文献:
[1] 张葛祥, 胡来招, 金炜东. 雷达辐射源信号脉内特征分析[J]. 红外与毫米波学报, 2004, 23: 477.
[2] 张葛祥, 胡来招, 金炜东. 基于熵特征的雷达辐射源信号识别[J]. 电波科学学报, 2005, 20: 440.
[3] Zhang G, Rong H, Jin W, et al. Radar emitter signal recognition based on resemblance coefficient features [C]//International Conference on Rough Sets and Current Trends in Computing. Berlin/ Heidelberg: Springer, 2004.
[4] Cohen L. Time-frequency analysis theory and applications [M]. New Jersey: Prentice Hall, 1995.
[5] 朱振波, 王玉生, 何明浩. 基于近似小波变换的信号脉内特征分析[J]. 空军雷达学院学报, 2002, 16: 8.
[6] Gao J, Dong X, Wang W B, et al. Instantaneous parameters extraction via wavelet transform [J]. IEEE T Geosci Remot, 1999, 37: 867.
[7] 郁春来, 万建伟, 徐如海, 等. 改进小波脊线法算法分析和仿真[J]. 现代雷达, 2005, 27: 46.
[8] Lopez-Risueno G, Grajal J, Yeste-Ojeda O. Atomic decomposition-based radar complex signal interception [J]. IEEE P-Radar Son Nav, 2003, 150: 323.
[9] 柳征, 姜文利, 周一宇. 基于小波包变换的辐射源信号识别[J]. 信号处理, 2005, 21: 460.
[10] 彭朝霞, 蒲亦非. 基于分数阶微分的卷积神经网络的人脸识别[J]. 四川大学学报: 自然科学版, 2022, 59: 012001.
[11] Zhang M, Diao M, Guo L. Convolutional neural networks for automatic cognitive radio waveform recognition [J]. IEEE Access, 2017, 5: 11074.
[12] 郭立民, 陈鑫, 陈涛. 基于AlexNet模型的雷达信号调制类型识别[J]. 吉林大学学报: 工学版, 2019, 49: 1000.
[13] Guo Q, Yu X, Ruan G. LPI radar waveform recognition based on deep convolutional neural network transfer learning [J]. Symmetry, 2019, 11: 540.
[14] Zhang M, Diao M, Gao L, et al. Neural networks for radar waveform recognition [J]. Symmetry, 2017, 9: 75.
[15] 肖易寒, 王亮, 郭玉霞. 基于去噪卷积神经网络的雷达信号调制类型识别[J]. 电子与信息学报, 2021, 43: 8.
[16] Peng S, Jiang H, Wang H, et al. Modulation classification based on signal constellation diagrams and deep learning [J]. IEEE T Neur Net Lear, 2018, 30: 718.
[17] Qin X, Zha X, Huang J, et al. Radar waveform recognition based on deep residual network [C]//2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC). Piscataway: IEEE, 2019.
[18] Wang Y, Liu M, Yang J, et al. Data-driven deep learning for automatic modulation recognition in cognitive radios [J]. IEEE T Veh Tech, 2019, 68: 4074.
[19] Wu Y, Li X, Wang Y. Extraction and classification of acoustic scattering from underwater target based on Wigner-Ville distribution [J]. Appl Acous, 2018, 138: 52.
[20] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need [J]. Proc Adv Neur Inf Process Syst, 2017, 2017: 30.
[21] Liu Z, Lin Y, Cao Y, et al. Swin Transformer: hierarchical vision transformer using shifted windows [C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Piscataway: IEEE, 2021.
