基于高斯混合变分自编码器的协同过滤

2023-04-29罗彪周激流张卫华

四川大学学报（自然科学版） 2023年6期

罗彪周激流张卫华

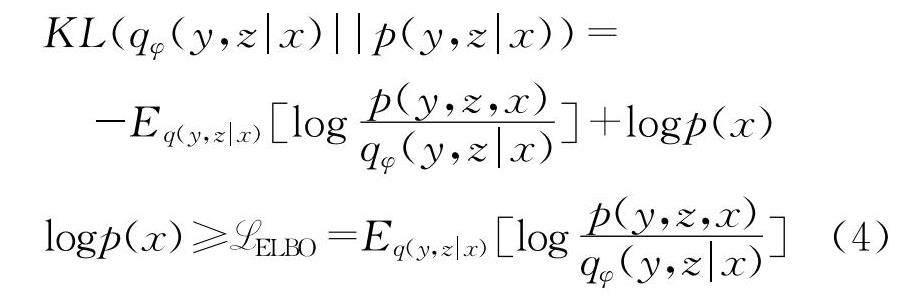
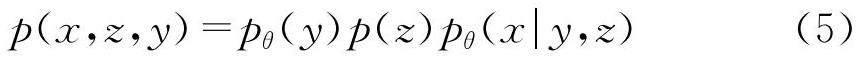
摘要：基于变分自编码器的协同推荐算法可以帮助解决推荐算法中的稀疏性问题，但是由于变分自编码器模型先验是单一的高斯分布，使得表达趋向简单和平均，存在拟合不足的问题.高斯混合变分自编码器模型拥有更加复杂的先验，相对于原本的变分自编码器模型，它对于非线性的任务有着更强的适应性和效果，已被广泛应用于无监督聚类和半监督学习.受此启发，本文研究基于高斯混合变分自编码器模型的协同过滤算法.本文基于Cornac推荐系统比较框架设计实验，将高斯混合变分自编码器改进后用于协同推荐任务中，利用生成模型重新生成的用户-物品矩阵进行推荐.在推理模型和生成模型中分别用一层隐藏层提取深层特征增加模型鲁棒性，并且使用提前停止的训练策略以减少过拟合.本文在多组公开数据集上进行实验，与其他推荐算法在NDCG和召回率指标上进行对比.实验证明，改进的基于高斯混合变分自编码器模型的协同过滤算法在推荐任务中表现优异.

关键词：协同过滤；变分自编码器；高斯混合；神经网络

收稿日期： 2022-04-24

基金项目：四川省自然科学基金（2022YFQ0047）

作者简介：罗彪（1998-），男，四川绵阳人，硕士研究生，主要研究方向为推荐系统.E-mail： 1726483356@qq.com

通讯作者：张卫华.E-mail： zhangweihua@scu.edu.cn

Gaussian mixture variational autoencoder for collaborative filtering

LUO Biao，ZHOU Ji-Liu， ZHANG Wei-Hua

（College of Computer Science， Sichuan University， Chengdu 610065， China）

The collaborative recommendation algorithm based on the Variational Autoencoder （VAE）can help solve the sparsity problem in the recommendation algorithm， but the VAE models prior is a single Gaussian distribution， which makes the expression tends to be simple and average， and suffers from the problem of underfitting. The Gaussian Mixture Variational Autoencoder （GMVAE）model has a more complex prior， which is more adaptable and effective for nonlinear tasks compared to the original VAE model， and has been widely used for unsupervised clustering and semi-supervised learning. Inspired by this， this paper investigates a collaborative filtering algorithm based on the GMVAE model. In this paper， the authors design experiments based on the Cornac recommender system comparison framework， and use the improved GMVAE for the collaborative recommendation task， the user-item matrix regenerated by the generative model is used for recommendation task. Deep features are extracted with one hidden layer in the inference model and one layer in the generation model to increase model robustness， and an early stop strategy is used to reduce overfitting. In this paper， experiments are conducted on multiple public datasets to compare with other recommendation algorithms in terms of NDCG and recall metrics. The experiments demonstrate that the improved collaborative filtering algorithm based on a GMVAE model performs well in the recommendation task.

Collaborative filtering; Variational autoencoder; Gaussian mixture; Neural network

1 引言

随着互联网的发展，往往有太多无用的冗余信息被展示在用户面前，用户在海量的数据信息中寻找真正需要的信息变得越来越困难.在这种情况下，推荐系统变得越来越重要，一个好的推荐算法可帮助用户有效地找到他所需要的部分数据.协同过滤算法是一种被广泛使用的推荐系统算法，协同过滤算法通过用户的历史数据计算用户或物品之间的相似性来进行推荐^[1].隐性的偏好数据往往可以表达成用户-物品评分矩阵，一些矩阵分解模型被用于协同过滤中，该方法相对简单^[²^，3].然而，因为只能捕获数据中的线性模式，这些早期的方法能力大多是有限的，这使得要适应更大的稀疏矩阵成为挑战.

许多情况下，在所有可能的用户与物品的互动中，只有不到1%的相互作用实际发生，也就是说用户-物品评分矩阵是一个巨大的稀疏矩阵，这被称为稀疏性问题，是协同过滤的一个重要的限制因素^[¹^，4].稀疏性问题不仅给矩阵分解方法带来了麻烦，而且给一些非线性神经网络方法也带来了很大的挑战和困难.这些神经网络方法的复杂性和确定性使其难以处理海量的稀疏数据.

变分自编码器（Variational Autoencoder，VAE）模型可以帮助解决稀疏性问题，且已经被应用于协同过滤推荐算法，体现出非常优越的性能^[5].变分自编码器是一种可通过神经网络构建非线性概率潜在模型的贝叶斯方法，它作为一种非线性神经网络方法，其性能优于矩阵分解等线性方法.与一般的神经网络不同，变分自编码器并不尝试学习特定的数据点，而是学习这些点上的潜在分布，从而让它具有解释潜在空间中的不确定性的能力^[6].

现有文献已报道各种变分自编码器模型及其改进模型^[^7].例如，Liang等人^[5]在生成模型中使用多项似然以及在参数估计方面使用贝叶斯推理，将变分自编码器用于隐性偏好数据的协同推荐.Li等人^[8]提出了一种考虑内容信息的协同变分自编码器，利用评分信息和内容信息，克服了协同推荐中的稀疏性和冷启动等困难.考虑到用户-物品评分矩阵是一种两路数据，Truong等人^[9]使用了一个生成模型和两个分别基于用户的和基于物品的推断模型，提出了双边变分自编码器.

变分自编码器利用神经网络捕捉数据的潜在特征，假设潜变量服从简单的高斯分布，而后对数据进行重构.在这样的前提假设下，变分自编码器存在的问题之一是使用单一的高斯分布作为模型的先验.这只是一种对大多数问题的折中近似，并没有捕捉数据的完整特征.有研究表明，这个简单的假设将鼓励变分自编码器适应尽可能扩散^[10]，这会导致模型对真实分布的拟合不足，更加倾向于一个接近平均的分布.

面对这样的情况，将简单单一的高斯分布扩展成为多个高斯的混合分布，就成了一个自然而然的想法.高斯混合变分自编码器（GMVAE）作为变分自编码器的一种变体，已经被广泛应用于半监督学习和无监督聚类中.高斯混合变分自编码器的主要思想是使用多重高斯分布取代传统变分自编码器的单一高斯先验.这种方式可以使得潜变量对于数据潜在分布的捕捉更加复杂，更加接近数据的真实分布，具有更强的学习能力.Kingma等人^[11]提供了高斯混合变分自编码器的概率模型并证明了生成方法可以有效地进行半监督学习. Dilokthanakul等人^[12]分析了一种使用混合高斯作为先验分布的变分自编码器，以便使用深度生成模型进行无监督聚类.Rao等人^[13]提出了一种方法（CURL）来解决一个他们称之为无监督持续学习的问题.CURL使用了一种潜在的混合高斯，这与高斯混合变分自编码器中使用的图模型类似. Collier等人^[14]表明，使用连续松弛法能在保持可接受的聚类质量的同时，大大减少训练时间.张显炀等人^[15]的研究中，利用高斯混合的变分自编码器实现了对海面舰船的轨迹预测，相比于传统的预测算法，取得了更好的预测结果.

现在已经有研究将高斯混合变分自编码用于协同过滤中，Charbonneau使用了这一模型应用于Tou.TV和MovieLens-20M数据集并且测试了他的模型效果^[16].文献[6]中模型在实现多重高斯时使用了多个不同的中间变量，有着更大的模型复杂度.与文献[6]不同，本文的模型只有一个中间变量，通过增加了一个网络结构实现了混合高斯，并且对模型进行了性能测试，在经典数据集上取得了优异的效果.

2 背景知识

在一个原始的变分自编码器中，潜变量的先验是一个固定的单一各向同性高斯分布.先验是一种对潜在分布进行的合理假设，它将作为一种潜在结构去影响变分自编码对于数据的学习和重构.如果数据的重新表达中包含单一高斯的先验，将使得表达趋向于简单和分散，对复杂的数据将拟合不足.这就需要选择更加合适的先验代替原先的简单高斯分布，来捕获更多结构层次的数据特征.从这个角度出发，已经有多种变分自编码的变体被发明，使其可以学习更复杂的潜在表征.在本研究中，选择高斯混合变分自编码器，通过假设数据可以被多个混合的高斯生成，可以对多层次的结构化人群分布特点进行建模并且捕获他们的潜在特征.

常规变分自编码器以x|w～N（μ_w，diag（σ²_w））作为先验分布，它常常面临拟合坍塌的问题，使得模型不能充分表达生成数据.将单一高斯变为多重高斯时，首先要面对的问题是：将无法计算Kullback-Leibler （KL）项，然而这个项是原来模型的学习优化算法中必须的.当变分后验分布遵循混合高斯^[17]时，变分自编码器中使用的积分^[^6]是不解析的.为了解决这个问题，引入了一种被用在无监督集群任务^[12]中的方法，如图 1所示.在基本的变分自编码器框架下，增加了一个过程来引入不同类别的标签y，分别参与生成模型和变分模型.与无监督或者半监督学习有所不同，无监督或者半监督学习中引入这个分类过程最主要的目的是对数据进行聚类任务，这个变量作为学习的主要目标来输出聚类的类别标签.在模型中，这个分类变量并不作为标签输出而是作为一个新增的潜变量对人群进行建模，通过已知数据学习数据的潜在表达，重构生成数据，最后利用重构生成的数据对用户进行推荐.

除了直接对个体和产品上的潜在分布进行变分自编码器学习外，本方法还包括了一个将人群聚集成更加具体的群体的过程.因此，可以将潜在空间划分为不同的类别，用混合高斯先验作为一种更加合适建模数据的结构，这对于推荐任务中的海量用户和物品，以及不同用户的潜在关联有着更好的适应性和拟合能力.这个模型中的推断模型是一个关键的问题，然而这个问题通过多种方法已经解决，并且可以通过标准反向传播进行优化.

3 基于高斯混合变分自编码器的协同过滤算法

3.1 生成模型

用u∈{1，…，U}表示所有用户编号，i∈{1，…，I}表示所有物品编号.矩阵X∈N^U^×I表示用户与物品的评分矩阵.在协同推荐任务中，通过生成模型来生成服从原始数据潜在分布的数据，利用生成的数据进行推荐.首先是生成模型p_θ（y，x，z）=p（y）p（z）p_θ（x|y，z）.x_u=[x_u1，…，x_uI]表示一个用户的用户向量，z表示了用户和物品的关系的潜在变量，y表示一个标识属于不同组的用户分布的先验变量.生成模型中描述重新生成的数据X由连续的潜在变量z和潜在的分类变量y生成，如下.

p（y）=Cat（y|π），p（z）=N（z|0，I），p_θ（x|y，z）=f（x;y，z，θ）. （1）

式中，将y看成一个额外的潜变量，y服从多项分布，通过对原始数据的后验分布p_θ（y|x）来得到，表示每个用户所属的个体组.z是一个潜变量，f（x;y，z，θ）是一个合适的似然函数，例如伯努利分布或者高斯分布，是一个有关潜变量的非线性变化，表示经过变分自编码器重构后的数据.在实验中是由深度神经网络来表示这个非线性函数的.

3.2 变分模型

q_φ（z|y，x）=N（z|μ_φ（y;x），diag（σ²_φ（y;x））），q_φ（y|x）=Cat（y|π_φ（x）），（2）

式中，q_φ（z|x，y）项服从受到y和x约束的高斯分布；μ_φ（y;x）是一个表示均值的向量；σ_φ（y;x）是一个表示标准差的向量；q_φ（y|x）服从一个受到x约束的多项式分布；而π_φ（x）是一个概率向量.函数μ_φ（y;x），σ_φ（y;x）以及π_φ（x）用深度神经网络表示.目标是找到一个q满足

q^*_φ（y，z|x）=argmin_q_∈QKL（q_φ（y，z|x）||p（y，z|x））（3）

要最小化q_φ（y，z|x）和真实分布p（y，z|x）在KL尺度上面的差异.可以通过下面的方式获得变分下界.

如图 1所示，将真实后验和估计分解如下.

最后得到了变分下界：

由于实际训练中没有关于y的标签，和 Kingma 等人^[11]不同的是本研究将y直接作为一个潜在变量，而不是输出作为一个标签.由此可见，混合高斯的作用主要是增加模型容量，使其适应更复杂的数据，而不是将其用于分类任务.

本研究使用了和Kingma 等人相同的方法，使用通过蒙特卡罗采样估算损失.可以使用下界来优化θ和φ，下界主要部分的梯度如下所示.

使用adaGrad优化器优化参数θ和φ，通过（θ_n+1，φ_n+1）=（θ_n，φ_n）+Γ（g_θ，g_φ），其中Γ（g_θ，g_φ）是一个梯度对角矩阵.训练过程如下所示.

4 实验与分析

本节开展了在公开的数据集上对GMVAE模型的实验，并分析了模型有效的原因.实验基于Cornac^[18^，19]，一个用于多模式推荐系统的比较框架.本实验用到的数据集、基线模型和指标都来自该框架.

4.1 实验设计

4.1.1 数据集

数据集如表1所示，对于所有的数据集，实验判断是否存在用户和物品的交互，并且将存在交互视为一种正反馈对数值评分数据进行二值化.

ML-100K， ML-1M， ML-10M以及 ML-20M是一组大小不同且常在推荐系统领域作为评价标准的数据集，它包含了用户对不同电影的评分，其中，每一个用户至少对20个电影进行评分.

Amazon clothing， Amazon office和 Amazon toy是一组由亚马逊提供的相对稀疏的数据集，包含了用户对物品的评分.另一个数据集epinions也包含了用户对产品的评分数据.

4.1.2 基线

将本模型与两个变分自编码器变体模型和另外两个基于协同过滤的模型进行比较.

（1）双边变分自编码器（BiVAECF）：BiVAE（Bilateral Variational Autoencoder）是一个变分自编码器系列模型，它以相似的方式对待用户和物品，并且更适合两路数据.此外，约束自适应先验（Constrained Adaptive Priors，CAP）提高了BiVAE的性能，增强模型的性能优于传统的VAE模型和其他几个类似的滤波模型^[9].

（2）变分自编码器（VAECF）：该模型是变分自编码器的扩展.与线性因子模型相比，它有更加优越的模型容量，同时它在一些真实的数据集上的表现优于不少最先进的基线^[5].

（3）层次化的泊松分解（HPF）：HPF（Hierarchical Poisson Factorization）是一种将用户和商品与两个潜在向量关联起来的概率模型.经证实，HPF的性能优于其他竞争方法，包括MF（Matrix Factorization）模型^[2].

（4）广义矩阵分解（GMF）：GMF（Generalized Matrix Factorization）由矩阵分解模型演变而来，并与神经网络相结合.利用神经网络取代内积的方式，改进了在推荐系统中被广泛使用的矩阵分解方法.与其他基于分解的方法相比，GMF有显著的提升^[20].

4.1.3 评价指标

选择了标准化折现累积增益（Normalized Discounted Cumulative Gain，NDCG）和召回率作为评价模型的两个标准措施.选择M=50作为top-M推荐.

4.1.4 实验设置

打乱数据集，将其分为训练集、验证集和测试集，分别占80%、10%和10%.在保留的验证集上，用NDCG作为基准调整了模型.表示人群类型数量的潜变量y的维度和表示用户物品关系的潜变量z的维度分别被设定为10和100.然而，这些参数的改变对实验结果并没有明显的影响.对于推理和生成模型，分别使用具有一个隐藏层的MLPs，使用整流线性单元（ReLU）函数作为每个隐藏层的激活函数.对于隐藏层，将其宽度设置为256，本研究发现使用更深或更宽的隐藏层结构没有让实验结果有明显的改善.在重建损失方面，当使用交叉熵而不是平均平方误差（MSE）时，取得了显著的改善.从{1e^-5，…，1e^-2}中选择1e^-4作为学习率，从{100，…，500}中选择100作为每轮的步数.对于使用Adam优化，批次大小被设定为128.与此同时，本研究还使用了早期停止策略来缓解模型的过度拟合.对于基线模型，使用Cornac中设置的默认参数.

4.2 实验分析

高斯混合变分自编码器与BiVAECF、VAECF、

HPF和GMF进行比较.如表2所示，模型在某些数据集上表现良好，但在其他数据集上则不然.模型在ML-10M和ML-20M数据集上取得了最好的效果，NDCG和Recall值同时较高，则表明模型有精准的推荐顺序且没有遗漏潜在的推荐物品，但在epinions数据集上则不然.

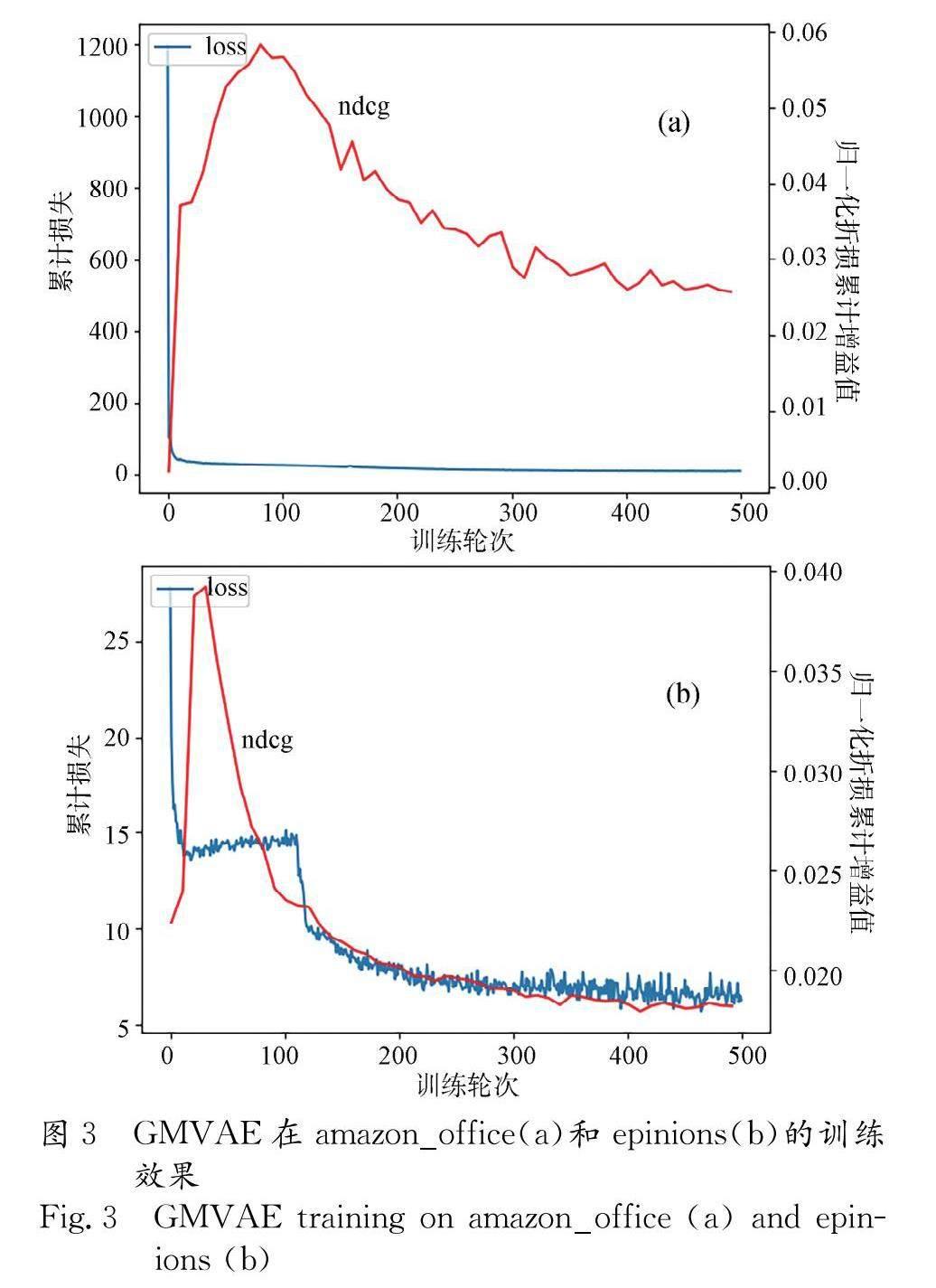
模型在更完整的数据集上表现得更好，这归功于混合高斯先验使得模型有更大的模型容量.混合高斯适用于预先对种群进行不同分类的假设，当用户数据量越来越密集时，这种假设更为合理.当用户数据较少时，由于很难对用户进行更清晰的分类，使得模型性能较弱.为了解释这一现象，本研究绘制了在不同的数据集上训练模型时的损失和NDCG.

在相对密集的数据集上，高斯混合变分自编码器的效果良好，而在稀疏的数据集上，它的效果不佳.模型在ML-100K上训练时，性能较早达到峰值，然而随着loss的不断下降性能开始变差，如图2所示.这一迹象表明，模型可能在过于稀疏的数据集上陷入过拟合.然而当模型在ML-20M上进行训练时，随着训练的进行，性能逐渐稳定在一个较高的水平上.如图 3所示，在相对稀疏的数据集amazon_office和epinions上，模型都受到了过拟合带来的不良影响.然而，可以简单地使用早停策略来获得一个不错的最终结果.

与传统的VAE模型相比，本文提出的模型假设人们可以被分配到不同的组中，同一组中用户行为相似.当用户群体规模较大时，这个假设是相对合理的，简单的单一高斯先验并不是一个好的选择.

从模型的复杂性来看，增加了模型的容量，使模型的先验假设能适应更大的数据集.对用户进行分类，使用对应的参数theta和phi，将原始的单高斯先验转化为混合高斯先验.在一个相对完整的数据集上，本研究所用方法取得了很好的结果，这说明混合高斯先验于真实场景是有效的，并且在实际应用中可以避免其过拟合时带来的副作用.

5 结论

协同推荐任务中的数据具有稀疏性，同时包括海量的物品和用户，而变分自编码器的单一高斯先验导致模型对数据拟合不足使模型趋向于分散和简单，难以适应协同过滤任务中的特征.本文构建了一个用于协同过滤任务的GMVAE模型.与一般VAE相比，该模型是一种对原有模型的自然拓展，通过假设数据可以从多个不同的高斯分布生成，增加潜变量推测数据从其中一个高斯分布生成，学习数据的潜在特征和结构，达到比原模型更好的适应性和拟合效果.相比于初始的变分自编码器模型，增加了潜变量让模型可以学习到更多潜在表达，更复杂的先验使模型具有更大的模型容量.在多个经典的公开数据集上测试本文模型时，在NDCG和Recall指标上取得了不错的效果.实验结果表明，GMVAE算法可以应用于推荐任务中.然而，在稀疏的数据集上进行推荐依然是一项非常具有挑战性的任务，未来的工作可能包括改进GMVAE存在的过拟合问题.

参考文献：

[1]Adomavicius G， Tuzhilin A. Toward the next generation of recommender systems： a survey of the state-of-the-art and possible extensions [J]. IEEE T Knowl Data En， 2005， 17： 734.

[2]Gopalan P， Hofman J M， Blei D M. Scalable recommendation with hierarchical Poisson factorization[C]//Proceedings of 31 th Conference on Uncertainty in Artificial Intelligence. Arlington： AUAI， 2015： 326.

[3]Koren Y， Bell R， Volinsky C. Matrix factorization techniques for recommender systems [EB/OL]. [2023-09-20]. https：//arxiv.org/pdf/1312.6114 v10.pdf.

[4]Sarwar B， Karypis G， Konstan J， et al. Item-based collaborative filtering recommendation algorithms[C]//Proceedings of the 10th International Conference on World Wide Web. New York： ACM， 2001： 285.

[5]Liang D， Krishnan R G， Hoffman M D， et al. Variational autoencoders for collaborative filtering [C]//Proceedings of the 2018 World Wide Web Conference. New York： ACM， 2018： 689.

[6]Kingma D P， Welling M. Auto-encoding variational bayes [EB/OL]. [2022-02-01]. https：//arxiv.org/pdf/1312.6114 v10.pdf.

[7]Girin L， Leglaive S， Bie X， et al. Dynamical variational autoencoders： a comprehensive review[J]. Found Trends Mach Learn， 2021， 15： 1.

[8]Li X， She J. Collaborative variational autoencoder for recommender systems[C]//Proceedings of the 23 th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2017： 305.

[9]Truong Q T， Salah A， Lauw H W. Bilateral variational autoencoder for collaborative filtering[C]//Proceedings of the 14th ACM International Conference on Web Search and Data Mining. New York： ACM， 2021： 292.

[10]Mi L， Shen M， Zhang J. A probe towards understanding gan and vae models[EB/OL]. [2022-02-01].https：//arxiv.org/abs/1812.05676.

[11]Kingma D P， Rezende D J， Mohamed S， et al. Semi-supervised learning with deep generative models [EB/OL]. [2022-02-01]. https：//arxiv.org/abs/1406.5298v2.

[12]Dilokthanakul N， Mediano P A M， Garnelo M， et al. Deep unsupervised clustering with gaussian mixture variational autoencoders[EB/OL]. [2022-02-01].https：//blog.csdn.net/weixin_44441131/article/details/106746139.

[13]Rao D， Visin F， Rusu A， et al. Continual unsupervised representation learning [EB/OL]. [2022-02-01]. https：//arxiv.org/pdf/1611.02648.pdf.

[14]Collier M， Urdiales H. Scalable deep unsupervised clustering with concrete GMVAEs [EB/OL].[2022-02-01].https：//arxiv.labs.arxiv.org/html/1909.08994.

[15]张显炀，朱晓宇，林浩申，等. 基于高斯混合-变分自编码器的轨迹预测算法[J].计算机工程， 2020， 46： 50.

[16]Charbonneau K B. Variational autoencoders with Gaussian mixture prior for recommender systems[D]. Montréal： ?cole De Technologie Supérieure， 2020.

[17]Hershey J R， Olsen P A. Approximating the kullback leibler divergence between Gaussian mixture models [C]//Proceedings of the 2007 IEEE International Conference on Acoustics， Speech and Signal Processing-ICASSP'07. Piscataway： IEEE， 2007.

[18]Salah A， Truong Q T， Lauw H W. Cornac： a comparative framework for multimodal recommender systems [J]. J Mach Learn Res， 2020， 21： 3803.

[19]Truong Q T， Salah A， Tran T B， et al. Exploring cross-modality utilization in recommender systems[J]. IEEE Internet Comput， 2021， 25： 50.

[20]He X， Liao L， Zhang H， et al. Neural collaborative filtering [C]//Proceedings of the 26th international Conference on World Wide Web. New York： ACM， 2017： 173.

引用本文格式：

中文：罗彪，周激流，张卫华. 基于高斯混合变分自编码器的协同过滤[J].四川大学学报：自然科学版， 2023， 60： 062002.

英文： Luo B，Zhou J L， Zhang W H. Gaussian mixture variational autoencoder for collaborative filtering [J]. J Sichuan Univ： Nat Sci Ed， 2023， 60： 062002.