青海省2000 重力基本网的精度分析

李延龙, 刘海红, 李小刚, 省天琛, 张永荥, 杨海鹏

（1. 青海省基础测绘院, 西宁 810001;2. 青海省地理空间信息技术与应用重点实验室, 西宁 810001）

0 引言

青海省是中国重要的资源大省, 重力框架是青海省测绘基准的重要组成部分, 在资源勘查、生态环境监测和地球动力学研究等方面具有重要作用。 我国重力基准随着时间的推移, 点位破坏、重力信息变化对国家重力基准的现势性和应发挥的作用都有一定的影响, 对于一些基础研究和实际工程的现势性需要还有相当程度的不适应性［1］。

我国现行的重力基准是2000 国家重力基本网［2］, 建设过程中由于当时仪器数量的限制, 总体布设的控制点尤其是重力基准点较少。 国家现代测绘基准体系基础设施建设（一期工程）完成后, 原国家测绘地理信息局在青海省6 个国家站完成了绝对重力测量, 初步建立了青海省2000 国家重力基本网。 青海省面积72 万平方千米, 6 个重力基准点难以满足工程和研究需求, 加密青海省2000 重力基本网可有效提高青海省大地水准面的现势性,为全省高精度、 动态、 统一的测绘基准保障提供重力基准服务［3］, 并在似大地水准面精化、 地震预报研究、 资源勘探、 防震减灾及经济建设中发挥重要作用［1］。

为了进行青海省2000 重力基本网的精度分析,本文研究了重力基本网的布设过程, 采用四台CG-5 型和两台CG-6 型相对重力仪进行静态试验和动态及一致性试验、 相对重力联测和数据处理, 本文所提及的所有数据与《测绘与空间地理信息》期刊第45 卷第12 期《青海省2000 重力基本网的构建》 中的数据为同一数据, 均为共同观测计算所得, 但本文通过研究相关数据对基本网的精度进行了分析, 发现各项精度指标均优于规范要求。

1 重力基本网的布设

青海省最早的西宁重力基本点建于1957 年,由原国家测绘局组建的第一支重力测量队施测,是国家重力网的组成部分, 当时全国施测重力基本点22 个, 一等重力点80 个。 1963 年～1965 年,原国家测绘总局第二大地测量队沿甘森至格尔木、格尔木至诺木洪、 诺木洪至茶卡、 茶卡至西宁等一等三角锁段、 祁连山测区, 在西宁基本重力点和塔尔丁一等重力点之间控制布设二等重力点,并在测区布设了加密重力点。 1975 年～1978 年,总参测绘局第一大地测量队在青藏高原地区施测了63 个二等重力点［4］。

1.1 勘选

青海省2000 重力基本网由26 个点组成, 充分利用省内已有的重力基准点, 在全省范围内均匀埋设了18 个基本点, 联测8 个已知点（基准点、 基本点、 引点）, 均匀分布在各州市, 优化了网形结构, 空间分布均匀［5］。 测段总数35 个, 包含祁连县至托勒段的支线、 10 个闭合环（环最大测段数5个）、 1 个附合路线, 具体位置如图1 所示。

图1 联测路线Fig.1 Diagram of joint survey route

在满足所勘选点位符合相关规范的基础上,综合考虑以下因素, 将所有重力观测墩均埋设在了当地气象局院内并委托给该气象局:

1）青海省部分区域人烟稀少, 缺水缺电, 对重力观测墩施工有一定难度;

2）气象观测场宽敞, 观测环境良好, 便于重力联测和重力观测墩维护。

1.2 埋石

建设重力观测墩要求严格, 为便于长期保存和方便观测, 防止受振动和季节温度变化带来的影响, 按以下六点要求施工埋设:

1）重力观测墩的混凝土一次性浇筑完成, 墩体内无钢筋, 混凝土强度规格不低于C25, 水泥规格至少是P·O32.5 以上;

2）观测墩采用钢质模板, 模板内径100 cm ×100 cm, 高度大于100 cm;

3）混凝土现场浇灌, 观测墩表面光洁, 四周表面无再修饰, 采用水平尺保证整个墩体表面水平;

4）重力观测墩顶面安装重力标志, 观测墩顶面与标志面齐平, 标志字头朝北;

5）重力观测墩置于原生土上, 观测墩墩体规格（长宽深）为100 cm×100 cm×100 cm;

6）重力观测墩四周需要做宽度为10 cm 且与观测墩同深的隔振槽, 隔震槽内充填粗砂, 在隔震槽之外用土回填并夯实。

2 重力仪检验与标定

青海省2000 重力基本网建设采用的四台CG-5型和两台CG-6 型相对重力仪重复测量精度为5 μGal, 读数分辨率为1 μGal 和0.1 μGal, 长期残余漂移小于20 μGal/天。 CG-5 型和CG-6 型相对重力仪熔凝石英弹性系统具有相对稳定性, 漂移的线性度很好, 能够精确测定其静态零漂, 从而有效改正零漂影响［6］。

为了确保观测数据的可用性及准确性, 在联测前需要对重力仪进行静态试验、 动态及一致性试验和比例因子标定。

2.1 静态试验

试验在西宁市南山基准点上进行, 室内温度变化小, 周围无振动干扰且地基稳定。 待仪器稳定后每半小时读数1 次, 连续观测48 h, 整个测试过程中仪器处于开摆状态, 经过固体潮改正后,结合读数的观测时间绘制仪器的静态零漂曲线［7］。如图2 所示, 以CG-6（C262） 和CG-5（C284） 为例,展示了静态零漂曲线呈线性关系及48 h 观测中静态零漂残余振幅在10 μGal 左右波动, 未超出相关要求的20 μGal。

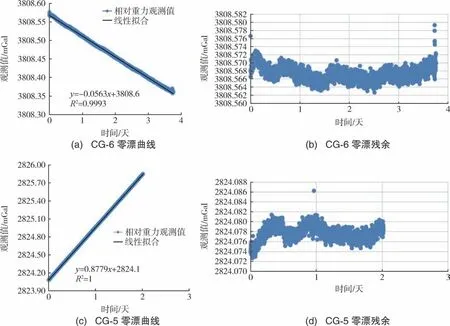
图2 静态零漂及零漂残余Fig.2 Curves of static zero drift and residual zero drift

2.2 动态及一致性试验

动态试验场位于西宁市湟中区满帐山, 共10个联测点, 点间最大段差约为90 mGal, 六台重力仪同时工作, 采用往返对称观测法完成3 个往返观测, 每个往返观测时间均超过8 h, 分别获得18 个观测数据, 经过固体潮和零漂改正, 得到每台重力仪的动态精度, 如表1 所示。 此次联测所有数据记录均采用天津天维科技开发有限公司的相对重力测量数据采集与处理系统, 该系统可实时计算出动态及一致性精度, 计算公式如下

表1 重力仪的动态精度计算结果Table 1 Calculation results of dynamic accuracy for gravimeters

式（1）中,mdy为一台仪器的动态观测精度, 单位为μGal;v为该仪器在同一相邻点间的各个段差观测值与平均值之差, 单位为μGal;l为该仪器所有测段段差观测值的个数;n为试验场地测段的个数。

六台仪器的一致性测试与动态测试一并进行,仪器间一致性中误差计算公式为

式（2） 中,mc为仪器一致性中误差, 单位为μGal;v为同一测段上六台重力仪段差观测值与平均值之差, 单位为μGal;m为六台仪器所有测段段差观测值的个数;n为试验场地测段的个数。 经过计算获得六台相对重力仪的一致性中误差为5.1 μGal,满足联测中误差限差2 倍的要求。

2.3 比例因子标定及联测

本项目比例因子标定采用重力差法, 该方法直观简便, 可快速检测格值系数变化带来的误差［8］。 标定区域位于共和（B070）至花石峡（B071）两重力基本点之间, 基线范围覆盖了实际基本重力测线分布范围的大部分, 采用往返对称观测, 每台仪器测定两个往返的结果, 两个结果之差小于40 μGal 时, 取其算术平均数作为该仪器的最终测定段差［5］。

因青海省内机场较少, 共和（B070） 与花石峡（B071）两基本点相距较远, 且都位于国道附近, 本次比例因子标定采用汽车联测方式。 比例因子标定需24 h 内完成联测, 为防止司机疲劳驾驶, 车辆配备了两位司机轮换。

相对重力联测路线布设时主要考虑了: 1）基准点与基本点整体联测成网; 2）每个直接联测路线闭合环边数不超过5 个［9］, 且联测时采用对称观测,即Ⅰ-Ⅱ-Ⅲ…Ⅲ-Ⅱ-Ⅰ, 对每个点位进行观测;3）在待测点上进行重力测量时, 每个点读数3 组,频率为1 s/个, 每组持续55 s, 取平均值作为该次读数的最终值, 每组读数间隔30 s, 相邻两组观测值互差未超过5 μGal［3］。

3 数据处理

3.1 相对重力测量数据预处理

（1）比例因子计算

本文使用的相对重力仪久置未用已超过两年,为保证观测数据精确有效, 重力观测数据处理之前, 对本项目重力联测所使用的CG-5 型和CG-6型相对重力仪进行比例因子计算。 通过式（3）可得六台重力仪的比例因子, 具体数值如表2 所示。

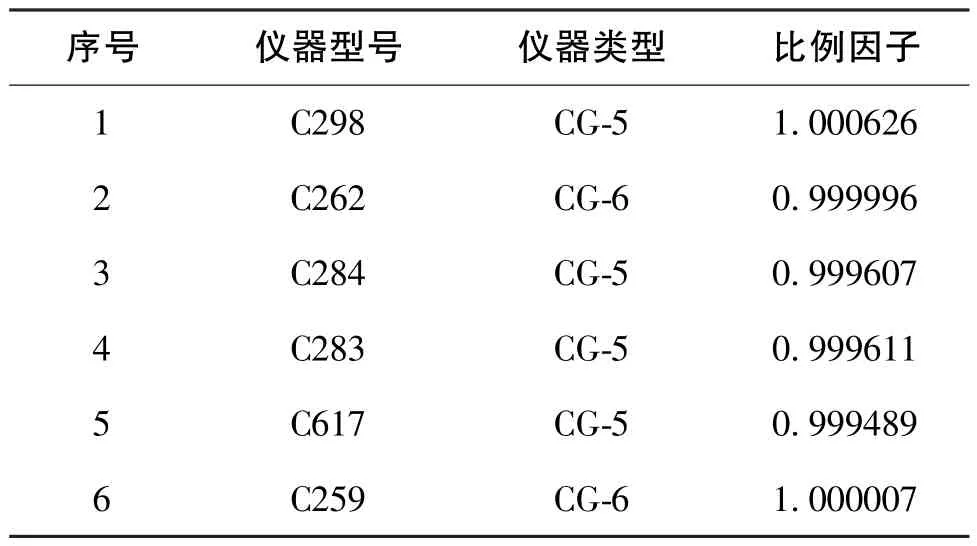
表2 重力仪的比例因子计算结果Table 2 Calculation results of scaling factor for gravimeters

式（3）中,C为重力仪的比例因子; ΔG12为两个标定点之间的已知段差, 单位为μGal; Δg12为两个标定点之间的实测段差, 单位为μGal。

（2）测线数据预处理

测线数据预处理包括仪器读数的格值转换、固体潮改正、 仪高改正、 气压改正、 零漂改正等各改正项计算及重力段差计算、 成果质量评定等内容, 测线数据经过预处理后获得平差数据, 对平差数据进一步平差计算, 最终获得各重力点的重力值。

固体潮改正采用零潮汐系统［10］, 计算公式为

式（4）中,δgt为固体潮改正值, 单位为μGal;δth为不同维度处各波群的理论潮汐值按振幅的加权平均值, 作为测站的平均潮汐因子;G（t）为理论重力体潮值;δfc为永久性潮汐对重力的直接影响。式（5） ～式（7）中,φ为测站大地纬度,ψ为测站地心纬度,F（φ） 为地球上不同维度处的影响因子,和cosZ为关于月亮的参数,和cosZs为关于太阳的参数, 以上几个变量的求解和推导见文献［10］附录部分。

仪器高改正的计算公式为

式（8）中,δgh为仪器高改正值, 单位为μGal;θ为重力垂直梯度, 单位为μGal;h为测站点的仪器高, 单位为m。

气压改正的计算公式为

式（9）、 式（10）中,δga为气压改正值, 单位为μGal;P为测点实测气压值, 单位为hPa;Pn为测点标准气压值, 单位为hPa;H为海拔高程, 单位为m。

将经过固体潮改正、 仪器高改正、 气压改正后所得的观测值称为初步观测值, 其表达式为

式（11） 中,gRC为初步观测值, 单位为μGal;gR为仪器读数, 单位为μGal。

零漂改正的计算公式为

式（12）中,δgk为零漂改正值, 单位为μGal;k为零漂率; Δt为测点的观测时间与起始点的观测时间之差。

零漂率计算公式为［11］

式（13） 中,g、g′、t、t′分别为测段起始点往返观测值和观测时刻,gi、g′i、ti、t′i分别为第i个静态观测点到达和离开时的观测值及相应的观测时刻。

经零漂改正后, 最后观测值的计算公式如下

式（14）中,gRZ为最后观测值, 单位为μGal。

利用35 个测段进行重力段差计算, 得到35 个段差成果, 计算公式如下:

段差最后观测值Δgij为

（3）数据质量统计

①段差联测中误差

同一测段的段差最后观测值中误差为

式（18）中,v为段差最后观测值的平均值与各段差观测值之差,n为段差最后观测值的个数。

经数据预处理共获得208 个观测量和35 个段差成果, 段差联测中误差最大值为7.2 μGal［12］,小于规范要求的10 μGal。

②环闭合差

由乘以格值一次项系数后的各仪器段差平均值（Δgm）为元素, 以最小环为原则进行拼环, 共构成10 个闭合环。 其中, 4 边环5 个, 5 边环5 个,具体如表3 所示。 环闭合差计算公式为

表3 环闭合差统计结果Table 3 Statistical results of loop closure error

式（19）中,ω为环闭合差, 单位为μGal; Δgi为第i个测段的最后观测段差, 单位为μGal;n为闭合环中的测段数。

环闭合差允许限差的计算公式为

式（20） 中,W0为环闭合差允许限差, 单位为μGal;m0为段差中误差的允许值, 单位为μGal。

3.2 平差计算

（1）平差方法

平差计算时, 相对重力观测量初始权值按等权1 赋值; 平差过程中, 相对重力观测量采用抗差估计重新定权, 抗差估计等价权模型参数:k0取为1.5,k1取为4.5,ε取为2 μGal; 平差同时顾及了6 台相对重力仪格值一次项误差的影响。 本项目的平差过程中, 采用抗差估计法对问题数据进行抗差和粗差剔除［13］。

将任一观测值的误差方程写为一般式［14］

式（21）中,vi为残差向量,ai为系数矩阵,X^为未知量向量,Li为观测量向量。 相对重力测量的权和绝对重力测量的权组成权阵Pi, 其等价权为［14］

解算采用迭代法, 第k+1 次解式为

基本点网是重力测量的基本控制, 要求有很高的精度, 因此必须顾及日月潮汐对重力的影响,对不同时间、 不同地点的重力观测值加以改正。如果要求精度很高, 还要顾及该地区的重力潮汐因子, 考虑到该地区的地球弹性影响［15］。

以经过固体潮改正、 仪高改正、 气压改正、零漂改正后的相邻两点的段差观测值作为观测量,则一台仪器在i点和j点之间的段差观测值的误差方程为［13］

式（26）中,gi、gj为测站i、j点平差后的重力值;gRZi、gRZj为测站i、j点经过四项改正的相对联测最后观测值;Ri、Rj为重力仪在i、j点的观测读数;CK为重力仪的K次多项式格值函数的K次格值改正因子, 一般情况K=1, 仅少数仪器K=2;Xn、Yn为仪器周期误差参数。

（2）平差策略

本项目以我国最新重力基准成果为起算进行整网平差计算, 共计采用8 个起算点, 点位信息如表4 所示。

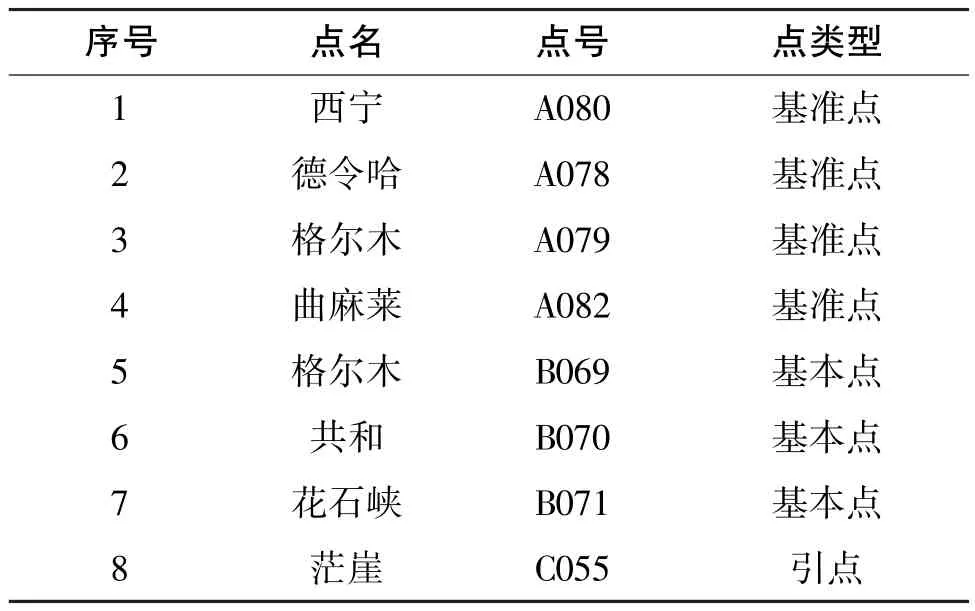
表4 起算点信息Table 4 Information of starting points

平差计算时, 以测线数据预处理获取的208 个观测量为输入数据, 经平差计算共获得18 个未知点重力值和6 台相对重力仪格值一次项成果［12］。

（3）精度评定

①内部精度评定

单位权中误差的计算公式为

式（27）中,m0为单位权中误差,V为段差最后观测值的平均值与各段差观测值之差,n为段差最后观测值的个数。

重力点点位中误差的计算公式为

式（28）中,Mi为待定点的点位中误差,m0为单位权中误差,Qii为待定点的协因数。

重力点平均值中误差的计算公式为

式（29）中,T为待定点的个数。

经平差计算, 单位权中误差为12.2 μGal, 重力点平均值中误差为4.3 μGal, 重力点值平均精度均优于15 μGal。

②偶然误差特性检验

残差共208 个, 其中正负号总统计为: 负号97 个、 正号111 个;

正负残差分布统计如表5、 图3 所示;

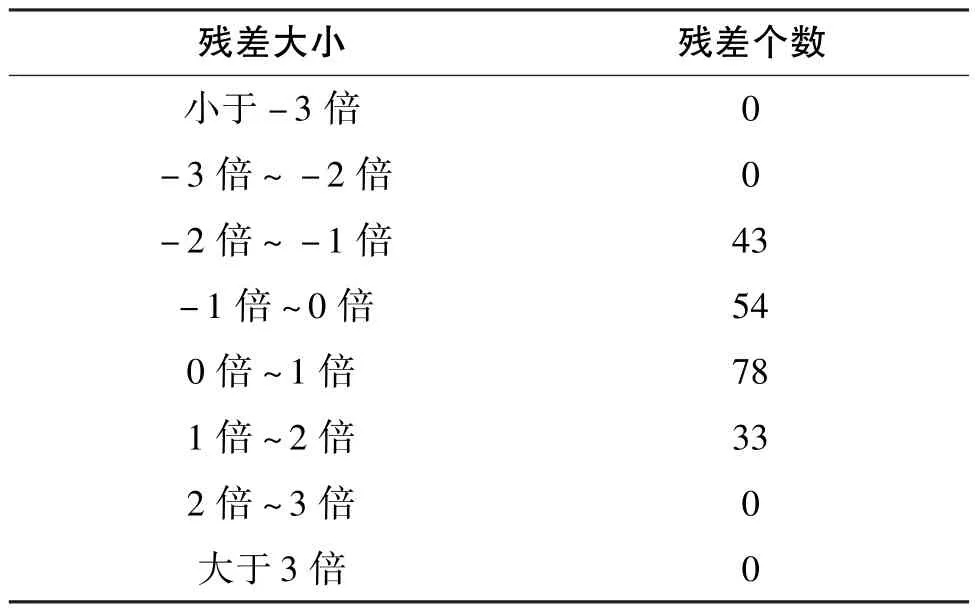
表5 正负残差分布Table 5 Distribution of positive and negative residuals

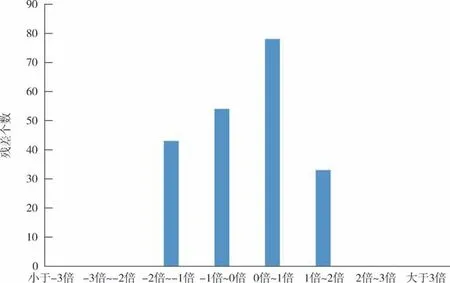
图3 正负残差分布柱状图Fig.3 Bar chart of positive and negative residual distribution

残差的数值和为: -101.281 μGal。

上述几项偶然误差特性检验结果表明: 平差误差分布符合正态分布［12］。

4 结论

本文在严格勘选、 埋设重力点位的基础上,利用四台CG-5 型和两台CG-6 型相对重力仪对26个点位采用对称观测法进行联测获得相关数据,并对测线数据进行预处理平差计算, 获得208 个观测量和35 个段差成果及18 个重力点成果, 具体结论如下:

1）青海省2000 重力基本网经数据处理获得35个重力段差成果, 联测中误差最大值为7.2 μGal;经平差计算获得18 个重力点成果, 平差后单位权中误差为12.2 μGal, 重力点平均值中误差为4.3 μGal。

2）青海省2000 重力基本网成果精度高, 实现了一二等水准测量, 与最新的国家重力基准和成果有效对接, 保持了与国家重力基准的一致性,完善了青海省测绘基准建设, 有效地满足了服务省级发展的需要, 在似大地水准面精化方面和地质矿产勘查方面具有广泛的应用前景［16］。

3）青海省2000 重力基本网的建设不仅有效改善了青海省此前 “2000 网” 基准点少的现实问题, 且青海省2000 重力基本网建设的整体思路、关键技术对于其他区域重力基准建设具有参考意义。

4）重力测量是大地单元划分、 深大断裂确定、结晶基底研究、 局部盆地圈定、 基底起伏研究的地球物理依据, 在青海省早期油气勘查、 煤炭勘查、 基础设施建设选址等方面起到了重要作用。当前, 青海省小比例尺区域重力工作程度相对较高, 1 ∶100 万重力全省覆盖, 1 ∶20 万～1 ∶25 万重力完成81 幅、 50 多万平方千米; 但大比例尺1 ∶5万重力测量仅仅在重点矿集区开展了示范性工作,完成面积约3000 平方千米, 工作程度极低, 需进一步加强。

目前, 中国计量院利用自主研制的激光干涉型和原子干涉型绝对重力仪, 通过主办国际比对和超导重力观测技术, 建立了不同技术体制相互旁证的国家重力加速度计量基准, 其测量不确定度优于1 μGal［17］。 在未来的重力测量中, 若能采用该类型绝对重力仪, 将有效提高工作效率和数据精度。