核电非能动安全壳冷却系统分离式热管上升管结构优化

摘 要 对应用于核电安全壳非能动冷却系统的分离式热管上升管进行结构优化，探讨同时改变上升管夹角和管径比（分支管与主管管径之比）或单独改变管径比两种方案对管内流动阻力损失的影响。结果表明：上升管夹角越小，管内阻力损失越少，夹角为20°时管内阻力损失降低了7.48%；两种优化方案中管径比分别为1∶1.55和1∶1.95的上升管阻力损失比改进前的小，管径比的不同对减少阻力损失的影响较大，最大降低了89.09%。

关键词 分离式热管换热器 核电非能动安全壳 上升管 结构优化 管内流动损失

中图分类号 TQ051.5   文献标识码 A   文章编号 0254?6094（2023）02?0232?12

分离式热管换热器因具有不需要外界动力就可以运行的特点而广泛应用于核电安全壳非能动冷却系统中［1～5］。分离式热管蒸发段的一排管束对应着冷却水箱中冷凝段的一排管束，两者用绝热管道连接，有多少组这样的管束就有多少根外接管道，外接管道的数量决定了核电安全壳上的开孔数量，而开孔数量越多，越容易削弱核电安全壳的强度，增加安全壳内放射性物质泄漏的风险。

为更好地发挥分离式热管换热器在核电安全壳发生事故后的导热能力，保证核电安全壳的安全性［6～8］，笔者以分离式热管为研究对象，对其蒸发段与冷凝段的连接管道进行结构上的优化改造，从而达到整合分离式热管的外接管路、减少开孔数量提高核电安全壳的可靠性和降低管内阻力损失的目的。

1 计算模型

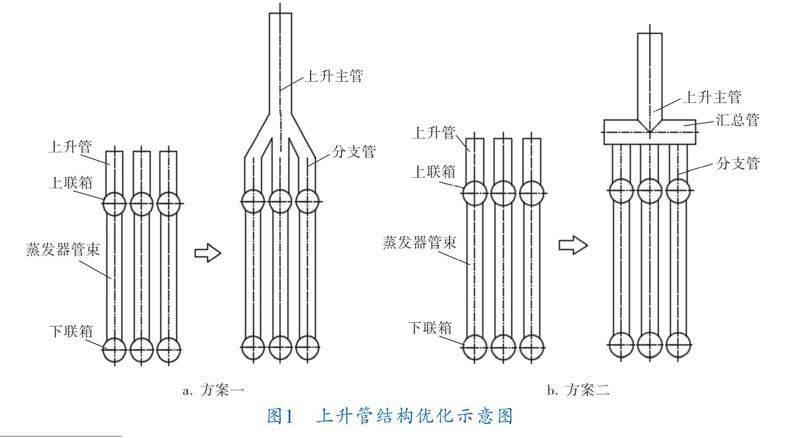
笔者提出了两种改进方案以减少管道数量，上升管结构优化示意图如图1所示。

方案一。直接将3根分支管与1根主管相连，形成斜四通管，在交汇处形成局部阻力，蒸汽通过上升主管流至冷凝段。

方案二。先将蒸发器3个独立的上升管与1根汇总管相连，此处由于管道突然扩大产生了局部阻力；蒸汽汇集后再流入1根上升主管（此处存在类似于三通接头的局部阻力），上升主管再穿至安全壳外到达冷凝段。

在达到减少阻力损失目标的同时，两种改进方案有以下几个优点：减少安全壳上开孔数量，提高其强度和密封性，进而强化安全壳安全性；现场管道布置清晰明了，节省管材，从根本上节约设备的制造成本；减少焊接工作量。

1.1 几何模型

以改进后的上升管为研究对象，两种优化方案的几何模型如图2所示。方案一模型由3根分支管和1根上升主管组成，蒸汽从分支管进入，在3根分支管交界处汇合后流入主管；方案二模型由3根上升分支管、汇总管和上升主管组成。蒸汽从分支管进入，在汇总管汇集后从主管流出，为排除流体的不稳定性对计算结果的影响，将分支管长度取5D1，上升主管长度取10D2，分支管规格为?140 mm×5 mm。直管均为无缝钢管，绝对粗糙度在0.01～0.05 mm范围内，本次模拟绝对粗糙度取0.03 mm。

1.2 数学模型

研究对象为饱和蒸汽在管内上升过程中的流动，考虑上升管为绝热管，管内流体流动不涉及传热过程，只通过连续性方程和动量方程来描述流体流动。为方便对改进后上升管流动情况进行模拟分析，模拟过程中对模型进行简化和假设［9］：计算过程中忽略浮力和重力的影响；默认入口处为饱和蒸汽；忽略管壁壁厚。

1.3 网格划分

利用Meshing分别对两种改进后的上升管三维模型进行非结构四面体网格划分，对管壁进行网格局部加密以提高计算精度，网格划分如图3所示。

1.4 边界条件设置

管内流动介质为蒸汽，管内不涉及传热过程，故不需要打开能量方程，管内流体在截面突变区域流动较为复杂，湍流模型选择标准k?ε湍流模型，设置速度进口、压力出口，无滑移绝热壁面，壁面粗糙度设置为0.03 mm，其他设置保持默认值，不存在传热过程，采用湍流强度和水力直径来描述湍流状态。求解方法选用SIMPLE算法，压力项选用PRESTO！格式。

1.5 网格无关性验证

对改进后两种方案的上升管三维模型采取四面体非结构化网格划分，计算4组不同网格数量下两种改进方案中上升管路的压降以验证计算的准确性，压降随不同网格数量的变化情况如图4所示，当网格数量越多时，压降变化幅度越小，在不影响计算结果准确性的前提下，按方案一改进的上升管选取网格数量为319 533的模型进行计算，按方案二改进的上升管选取網格数量为339 646的模型进行计算。

2 改进方案一数值模拟分析

对按照方案一改进的上升管模型进行数值模拟，分析不同夹角和管径比（分支管与主管管径之比）对四通管内流动特性和阻力损失的影响。取管径比1∶1.55的四通管进行管内流动模拟分析，入口流速15 m/s，分支管与主管夹角为20°，截取四通管中心截面速度云图、速度矢量图、压力云图和湍动能图进行分析。图5a为四通管中心截面速度云图，图中流体在分支管内流动稳定，各个分支管内流体向主管汇聚，且沿着主管入口方向速度逐渐增大，分支管与主管夹角较小，各分支管内流体进入主管过程中无明显掺混现象，流速分布比较均匀，主管内流体流速趋于稳定。图5b为四通管中心截面流体速度矢量图，从图中可以清晰地观察到流体流动轨迹和速度的变化，各个分支管内流体在经过分岔口时经过相互掺混形成了主管内的流体，两侧分支管内的流体在汇入主管时，由于管道方向的改变，流体在冲撞壁面后流动方向与中间分支管流体流动方向形成一定夹角，故在分岔口处由于不同来流方向流体的撞击，流体相互碰撞，加剧能量的传递与消耗，在交汇处和主管管壁处的湍动强度较大。从图5c可以看出，管内压力随着流体流动方向线性下降，分支管流道发生改变后，管内流体碰撞管壁压力增大；流体在分岔口汇合后，流体流通截面变大，压力随之减小，上升管内压力最小处出现在上升管主管入口近壁面处，进入主管后管内压力趋于稳定。从图5d可以看出，分支管与主管夹角较小，管内流体流动状态稳定，各分支管内流体流至分岔口时流体之间发生轻微扰动，无剧烈撞击，在各分支管内流体相互交汇处产生了湍动能；流体汇集后流入主管，流通截面突然缩小，流体间相互撞击，湍动能在主管入口管壁处最大。

2.1 夹角对上升管阻力损失的影响

在管径比、流速均相同的情况下，分析不同夹角对管内流体流动特性和流动阻力的影响。图6为管径比为1∶1.2、流速为15 m/s时，25、30、35、40°这4种夹角下上升管内流体流动速度云图，从图6中可以看出，夹角的变化对主管内流体流速无明显的影响，管内速度变化较小；流体流经分岔口处，各分支管流体汇集，速度增大，随着夹角的增大，分岔口处流体流动状态越不稳定，流体流至主管处碰撞越激烈，因此加剧了能量的传递与消耗，故管内的阻力损失随着夹角的增大而变大；且流体与管壁产生的分离区域随着夹角的增大而变大，即斜支管内壁处速度为零的区域变大，主管入口处近壁面处的速度也因为产生了垂直于流动方向的速度梯度而明显小于远离壁面处流体的流速。

图7为上升管内流体流速矢量图，从图7中可以看出，夹角为25°和30°时的上升管，各分支管内流体在分岔口交汇处无明显摩擦与碰撞，流体流动方向没有发生明显改变，管内流体流动较平稳；夹角增大至35°和40°时，上升管分岔口处流体开始出现轻微碰撞的现象，流体之间相互碰撞掺混的同时消耗机械能。随着夹角的增大，机械能消耗得越多，阻力损失随之增大。

图8为4种夹角下上升管内流体压力云图，流体流经分岔口处压力变化较大，3根分支管内流体流经分岔口处掺混严重，流速发生剧烈变化，流型不稳定，产生了较大的局部损失，根据能量守恒原则，流体在流至分岔口处压强迅速减小。

随着夹角的增大，流体在管道形状发生变化后流体逐渐脱离壁面，在斜支管内出现了分离现象，且随着夹角增大，分离区域越来越大，在分岔口处流体之间碰撞较为明显，搅混现象较为严重；流体从分支管流至主管时由于流动轨迹发生改变，夹角为25°时，上升管主管入口管壁处出现小区域的负压现象，且随着夹角的增大，主管入口管壁处负压区域越来越大。结合图9所示4种夹角下上升管内流体的湍动能图，夹角大的上升管在流向发生改变时较夹角小的上升管产生的湍动能大，当流体从分支管进入，经过分岔口时各个分支管内的流体相互撞击掺混形成了主管内的流体，由于流体间的相互作用，在主管管壁处湍动能最大，随着夹角的增大，流体在分岔口处的撞击越激烈，对主管管壁处的湍动能影响就越大，阻力损失较夹角小的管道要多。相反，夹角小的管道流体在流经分岔口处，流动方向相差不大，不会产生较明显的碰撞，流速较为均匀，湍动能小，故阻力损失较小。

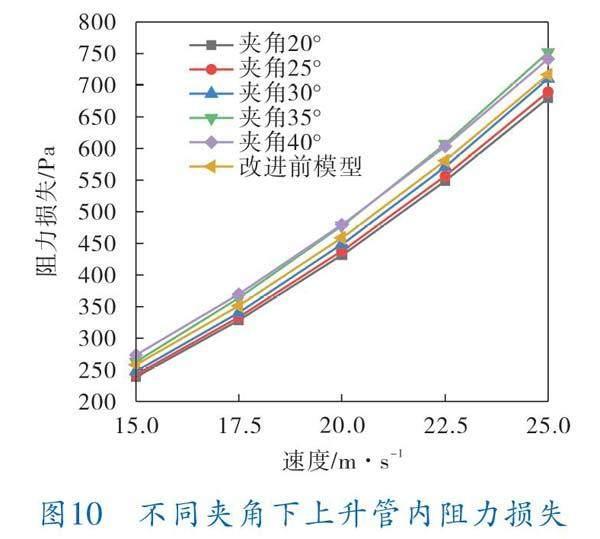
图10为不同夹角下上升管内阻力损失与改进前上升管阻力损失对比图，由图可以看出，速度不变时，管内阻力损失随着夹角的增大而略微增大，夹角的改变对管内阻力损失的影响并不显著，速度为15 m/s时，夹角为20°的上升管阻力损失为238.77 Pa，夹角为40°的上升管阻力损失为273.57 Pa，改进前上升管阻力损失为258.06 Pa；夹角为20°的上升管比夹角为40°的上升管阻力损失减少了12.7%，比改进前上升管阻力损失减少了7.48%；速度为25 m/s时，夹角为20°的上升管阻力损失为679.63 Pa，比速度为15 m/s时阻力损失增大了1.85倍；可以得出夹角相同时，速度越大，管内阻力损失明显增大。由阻力损失公式可以看出，管内阻力损失与速度的平方成正比。对比改进前上升管的阻力损失可以看出，夹角为40°时管内阻力损失大于改进前的阻力损失，其余3种夹角下的管内阻力损失均小于改进前管内的阻力损失，夹角越小，阻力损失越小，因此对于改进后的上升管应尽量选取夹角小的上升管来减少阻力损失。

2.2 管径比对上升管阻力损失的影响

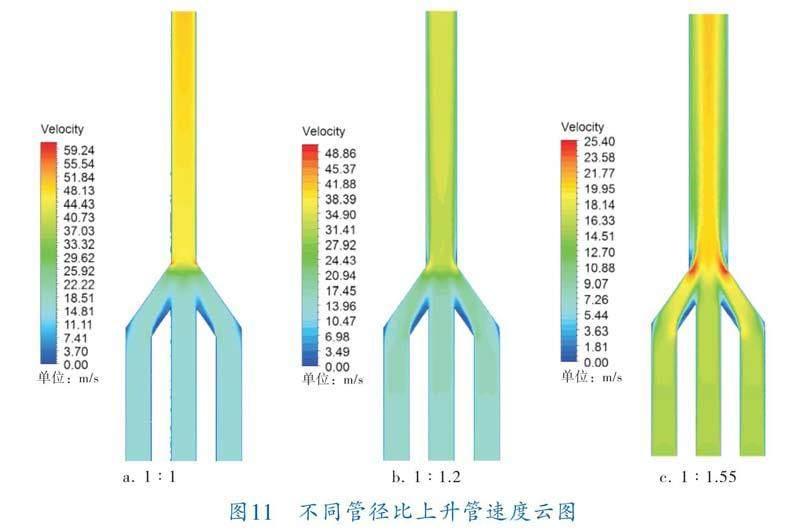
当夹角与流速不变时，分析不同管径比对管内流动阻力损失的影响。图11为不同管径比上升管中心截面速度云图，可以看出，出口处的速度随着管径比的增大而减小，管径比越大，主管的流通面积越大，在总流量不变的情况下，主管内流体流速随着流通面积的增大而减小；两侧分支管形状发生改变后，流体流动方向随之发生改变，导致分支管靠近内侧的管壁流体流动出现分离区，同种现象也出现在主管入口处管壁两侧，且随着管径比的增大，主管管壁处分离现象越明显，导致管子近壁面处流体的速度明显小于远离壁面处流体的速度。图12为不同管径比上升管内流体速度矢量图，从图中可以看出，不同管径比下的上升管内流体运动方向基本上是沿着上升管的轴向方向进行流动，分支管与主管之间有斜支管過渡，运动比较平稳，各分支管内流体运动无明显的碰撞和回流的现象。管径比为1∶1时，流体从分支管流入主管后，主管内速度分布均匀，管径比为1∶1.2时，分支管内流体按原来的流动状态进入主管，随着主管管径的增大，导致主管内壁面速度小于管内中心速度，管径比为1∶1.55时，此种现象更加显著，流体从管径小的分支管流入管径大的主管时，在分岔口处流体的碰撞产生了其他方向的分速度，造成了一定的流动损失；管内总流量不变，主管内速度随着管径比的增大而减小；由于流通几何结构变化和主管管径的增大，在垂直于主管流体流动方向上产生了明显的速度梯度，导致主管入口处近壁面流体速度相对较小。

图13为不同管径比上升管中心截面压力云图，图14为不同管径比上升管中心截面湍动能图。从图13压力云图中可以看出，在管径比变大的过程中，上升管内压力分布处于均匀状态，管径比的变化对上升管进出口的压力分布影响不大，在分支管与主管交叉处压力有明显的随着管径比的增大而降低的趋势。管径比为1∶1时的上升管管内压降为536.6 Pa，管径比为1∶1.55的上升管管内压降为78.9 Pa，说明管径比越大，管内压降越小，管内阻力损失则越小。当管径比变大时，管内流体总流量不变，主管内流体流速减小，降低了流体对管壁的摩擦，使得压降减小。从图14湍动能图中可以看出，管径比越大，湍动能越小。当管径比为1∶1时，斜支管内壁面与主管入口处内壁面产生了较大的湍动能，产生的区域较小，管径比为1∶1.55时，斜支管内壁面与主管入口处内壁面较大区域产生了湍动能，近壁面处的湍动能小于远壁面处的湍动能，与压力云图结果相符合，管径比越大，阻力损失越小。

图15为改进后不同管径比上升管与改进前上升管阻力损失对比图，从图中可以看出，同等速度下，分支管与主管的管径比越大，管内阻力损失越小，速度为15 m/s时，管径比为1∶1的上升管阻力损失为535.6 Pa，管径比为1∶1.95的上升管阻力损失为48.15 Pa，阻力损失大幅降低；管径比相同的情况下，流速越大，阻力损失越大，且随着管径比的增大，阻力损失增大趋势随着流速的增大改变不大。改进后上升管管径比为1∶1和1∶1.2时，管内阻力损失大于改进前阻力损失，改进后上升管管径比为1∶1.55和1∶1.95时，管内阻力损失小于改进前阻力损失；速度为15 m/s时，分支管与主管管径比为1∶1.55 和1∶1.95时，阻力损失分别为78.87、28.16 Pa，与改进前上升管阻力损失相比分别减少了69.44%、89.09%，管内阻力损失明显小于改进前的上升管阻力损失，两种管径比下减少的阻力损失相差不大，因此根据现实情况选取合适的管径比可以有效地减少上升管内的阻力损失。

3 改进方案二数值模拟分析

3.1 管径比对流体流动情况的影响

对管径比为1∶1.2、1∶1.55、1∶1.95的上升管进行数值模拟，分析管内流体的流动特性和阻力损失。对上升管中心截面处的流体流动情况进行分析，图16为不同管径比上升管中心截面的速度分布云图。从图16上升管中心截面速度分布云图中可以看出，流体在分支管内流动稳定，各个分支管内流体在汇总管聚集，流通截面突然扩大，速度减小，汇总管两端速度明显低于流体主流速度，流体从汇总管进入主管，流通截面突然缩小，在主管入口处速度明显增大，管内速度最大区域出现在主管入口处，在主管入口两侧壁面流速明显小于管内中心处速度，流体在主管上升过程中流速趋于稳定。随着管径比的增大，汇总管和主管内速度均有所减小，管径比为1∶1.95时，主管入口处速度与分支管内速度无明显增大现象。图17为不同管径比上升管中心截面速度矢量图，从图中可以清晰地观察到管内流体的流动轨迹。流体进入汇总管由于速度较大，两侧上升管内的流体冲击汇总管上部，一部分流体流至汇总管端部形成漩涡区，故两端速度较慢，另一部分流体与中间上升管内流体汇集一起流入上升管主管，由于流速较大，两侧流体在进入主管时由于管道结构的变化导致流体流动方向向中心倾斜，导致主管入口处近壁面处小于远离壁面处流體速度。两侧分支管内流体撞击汇总管上壁后流体方向发生改变，运动方向由竖直运动慢慢过渡到水平方向，与从中间分支管流出的流体在主管入口处相遇发生碰撞，故主管入口处的流体运动轨迹较为复杂，且随着管径比的增大，主管入口处的流体运动趋于平稳。

3.2 管径比对管内压力的影响

图18为不同管径比上升管内中心截面压力云图，分支管和主管管内压力比较稳定，连接分支管和主管的汇总管结构发生明显变化，流体在流至汇总管时，流通面积突然增大，管内压力逐渐降低，由于流体与管壁发生碰撞摩擦，在汇总管内下壁面压力较小，上壁面出现局部压力增大现象，此处主要克服因几何形状变化而产生的局部阻力。在蒸汽从分支管流进主管后，在主管入口壁面处形成了低压回流区，靠近壁面处管内压力明显小于主管内其他区域压力，随着管径比的增大，上升管内进出口压力随之减小，这主要是因几何形状发生改变而产生局部阻力损失，因此，管径比越大，管内产生的局部阻力损失越少。改进后上升管结构参数的变化会影响蒸汽在管道内的流动情况，流体流速也会影响管内的局部阻力，流速增大会使管内局部阻力增大，基于改进后的上升管，分析不同管径比上升管内阻力损失。

3.3 管径比对湍动能的影响

从图19不同管径比上升管湍动能图中可以看出，管径比为1∶1.2时，各分支管的流体在汇总管内交汇，流动出现轻微的碰撞，产生了较小的湍动能，流体汇集后进入主管，流通截面突然缩小，在主管入口近壁面处出现了回流区域，流动出现不稳定情况，此处产生了较大的湍动能，最大约为194 m2/s2，管径比为1∶1.55的上升管湍动能最大约82 194 m2/s2，管径比为1∶1.95的上升管湍动能最大约为35 m2/s2，可以看出管内湍动能随着管径比的增大而减小，管内阻力损失也随之减小。

3.4 管径比对阻力损失的影响

为了分析上升管管径比对整体上升管的流动阻力性能影响，在确保其他参数相同的情况下，对不同管径比的上升管进行数值模拟分析，不同管径比的上升管在不同入口流体速度下的阻力损失如图20所示。从图20中可以看出，管径比为1∶1.2的上升管内阻力损失比改进前原模型阻力损失大，当速度为15 m/s时，管径比为1∶1.2的上升管阻力损失为473.74 Pa，改进前的阻力损失为258.06 Pa，与改进前的上升管相比，阻力损失增加了83.58%，；速度增大后管径比为1∶1.2的上升管阻力损失分别为647.55、842.90、1 060.77、1 315.27 Pa，因此上升管管内阻力损失随着速度的增大而增大。管径比为1∶1.55和1∶1.95时，改进的上升管阻力损失比改进前的阻力损失小，速度为15 m/s时，管径比为1∶1.55和1∶1.95的上升管内阻力损失分别为160.08、59.94 Pa，比改进前上升管阻力损失减少了37.97%、76.77%，管内阻力损失大幅降低，可以得出只要管径比相对大，这种改进方法能够有效地减少阻力损失。

方案一上升管夹角对管内阻力损失影响较小，为了比较两种方案，忽略夹角对阻力损失的影响，由图15和图20可以看出，速度为15 m/s，管径比分别为1∶1.55和1∶1.95时，方案一上升管比方案二上升管阻力损失分别减少了50.73%、52.02%，且方案二上升管内冲刷严重，因此按方案一改进的上升管比方案二上升管好。

4 结束语

通过模拟分析改进后的两种上升管模型，分析其结构变化对管内流动特性及阻力损失的影响，与改进前后上升管的阻力损失进行对比，得出按方案一改进的上升管管径比为1∶1.55时，上升管阻力损失比改进前的上升管阻力损失小；夹角小于等于30°时，管内阻力损失小于改进前上升管阻力损失，由此证明选择合适的管径比和夹角，按照方案一改进后的上升管是可以减小阻力损失的。按方案二改进的上升管选取合适的管径比也能达到相似的效果。改进后的上升管结构可以替代原上升管，一方面减少了分离式热管的连接管路数量，节省管材；另一方面安全壳上的开孔数量大量减少，有效提高安全壳的密封性和安全性，确保非能动冷却系统的稳定运行。

参 考 文 献

［1］ 王凯，王俊哲，叶晓丽，等.一种非能动的安全壳热量排出结构：CN110400644A［P］.2019-11-01.

［2］ 林诚格.非能动安全壳先进压水堆核电技术［M］.北京：原子能出版社，2010.

［3］ 李小华，何列，李世祯，等.浅谈核能和核技术的和平利用［J］.核安全，2019，18（3）：1-10.

［4］ CHENG H，WU Y，SONG D.HPR1000 advanced pressurised water reactor with active and passive safety［J］.Nuclear Future，2016，12（4）：38-43.

［5］ YU Y，NIU F，WANG S，et al.One?dimensional model for containment in AP1000 nuclear power plant based on thermal stratification［J］.Applied Thermal Engineering，2014，70（1）：25-32.

［6］ 武松.日本核泄漏事件背景下的中国核电［J］.中国科技产业，2011（4）：56-58.

［7］ 蔡骏驰.大空间内混合与热分层试验研究［D］.北京：华北电力大学，2015.

［8］ MAIO F D，NICOLA G，BORGONOVO E，et al.Invariant methods for an ensemble?based sensitivity analysis of a passive containment cooling system of an AP1000 nuclear power plant［J］.Reliability Engineering & System Safety，2016，151：12-19.

［9］ 徐梦娜.T型管内雾状两相流相分离及压降特性数值研究［D］.济南：山东大学，2017.

（收稿日期：2022-06-03，修回日期：2023-03-18）

Structural Optimization of Separated Heat Pipe Riser in Passive Containment Cooling System of Nuclear Power Plant

WU Qiong

（College of Mechanical and Power Engineering， Nanjing Tech University）

Abstract   In this paper， the structure of separated heat pipes riser pipe applied in the passive cooling system of the nuclear power containment was optimized. In addition， improving the riser pipes included angle and the diameter ratio （the ratio of branch pipe to main pipe diameter） or changing the diameter ratio of pipe was discussed to investigate their influence on in?pipe flow resistance loss. The result shows that， the smaller included angle can result in less in?pipe flow resistance loss. When the included angle is 20°， the in?pipe flow loss can be reduced by 7.48%. In the two optimal schemes， the flow resistance loss from the riser pipe with a diameter ratio of 1∶1.55 and 1∶1.95 respectively is smaller than that from the original riser pipe. The difference of diameter ratio has a great influence on reducing the flow resistance loss， with a maximum reduction of 89.09%.

Key words    separate heat pipe heat exchanger， nuclear power passive containment， riser pipe， structure optimization， in?pipe flow resistance loss

作者简介：吴琼（1998-），硕士研究生，从事换热器、热管的研究，1913908572@qq.com。

引用本文：吴琼.核电非能动安全壳冷却系统分离式热管上升管结构优化［J］.化工机械，2023，50（2）：232-243.