战时装备损坏程度分布预计方法研究
2023-04-28李明雨高鲁刘彬李凯
李明雨,高鲁,刘彬,李凯
(1.陆军工程大学石家庄校区 装备指挥与管理系,河北 石家庄 050005;2.陆军步兵学院石家庄校区 军政训练系,河北 石家庄 050227)
随着高新技术的飞速发展,战争形态已从机械化向信息化、智能化逐步转型。对称条件下的局部战争更加凸显“高精度、强火力、远距离”的特点,装备维修保障作为战斗力的“倍增器”,可为部队作战提供持续动力,其重要性不言而论。装备损坏量和损坏程度分布作为“量”和“质”的双维度考量,是战时装备损坏测算的核心内容,只有同时获得,才能为战时装备维修保障筹划与实施提供依据。笔者重点对战时装备损坏程度比例开展研究,推进战时装备损坏情况的细粒度预测,为装备维修保障任务分工和维修资源的配置优化提供理论支撑。
1 相关概念分析
战时装备损坏程度分布是战时装备损坏测算的关键环节,而单装的损伤程度是集群装备损坏程度分布的具体体现。应根据战场维修的经验判断和装备损坏的试验统计,实现对战时装备各损坏程度的比例预计。
1)战时装备损坏。指妨碍装备完成任务且需要排除或解决的事件,主要包括:战斗损伤、偶然故障、自然损耗故障、人为操作故障、装备缺乏供应以及环境不适应等[1]。其中,战斗损伤既包括受炮弹、导弹等的硬损伤,还有光、电、磁、网等的软损伤;偶然因素、自然损耗、人为操作故障等在战时更加严重;而作战环境造成的装备不适应损坏也是不容忽视的突出问题。
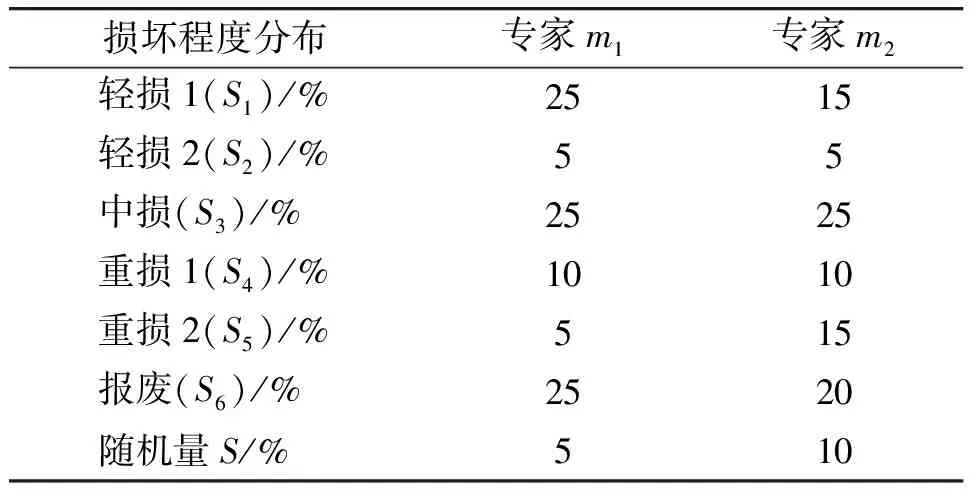
2)装备损坏程度。装备损坏程度,对应损坏功能影响程度和损坏修复的难易程度,常以战时装备损坏等级表示。一般可从装备功能影响程度、损坏修复时间、维修力量级别等不同维度进行装备损坏程度的判定,总体来说分为轻、中、重、报废4个等级,随着研究的不断深入,详细且精确的等级分类更利于装备损坏与维修任务的精准对接。参考业界学者研究,可进一步区分细化为6个等级[2-3],如表1所示。
3)装备损坏程度分布。装备损坏程度分布是指装备各损坏程度所占的比例,其中,作战样式不同、装备类型差异、敌对威胁强度都会影响战时装备损坏程度分布。一般运用理论计算法和经验推算法求得其损坏程度分布,如某类装备损坏按照轻损40%、中损20%、重损10%、报废30%区分[4-5]。在当前精确化、智能化战争的大背景下,“粗放型”“模糊型”的损坏等级分布比例已难以保证战时装备维修保障测算精度,难以满足战时维修保障筹划实施的现实需要。因此,对于战时装备损坏程度分布预计的方法研究可提升其可信度和可靠性,则具有较强的紧迫性和必要性。

表1 战时装备损坏等级分类
2 装备损坏程度分布预计因素分析
装备损坏程度的明确为装备维修保障的任务分工、力量配置和组织实施提供重要依据。战时装备损坏程度分布实质上是战时装备各损坏程度的数量占比求解问题,而其首要任务是深入剖析量化战场条件对其分布比例的影响。在装备损坏程度分布预计时,要充分利用现有类似装备损坏程度分布数据。充分考虑装备损坏机理、战场环境条件等要素的特殊性,对现有同类或相似装备各损坏程度占比加以改进修正,形成所求装备的损坏程度分布。笔者研究的是没有现有类似装备损坏程度分布可参考的情况。从微观具体维度看,各损坏程度的装备数量是基于单装损坏程度判定后的对应聚类集合,单装损坏程度是集群装备损坏程度分布的基本组成元素。因此,从“打”的微观维度出发,可基于战术对抗的损坏模拟,重点从单装损坏程度判定的影响因素进行分析;从“修”的宏观维度出发,可面向维修保障的需求考量,重点对装备损坏程度分布进行修正。
2.1 基于战术对抗的装备损坏程度判定因素
基于战术对抗、面向敌方威胁,从敌方对装备的损坏能力、威胁打击特性和装备自身的抗打击能力3个方面逐个分析装备损坏程度的影响因素。
1)敌方对装备的损坏能力,反映敌方对装备的损坏能力与装备损坏程度的正相关关系。主要指敌方对该装备的打击手段、精度和强度,一般以打击该装备的敌威胁战斗力指数量化。
2)威胁打击特性,反映威胁对装备打击时的具体特性参数,是装备损坏的最直接的影响因素。一是爆炸类型,区分空爆和地爆两种类型;二是威胁落角,指威胁和地面间的夹角,影响装备损伤形式和程度;三是弹着点相对目标位置,指装备中心和炸点连线与装备方向线的夹角;四是炸点与装备的直线距离,是装备损坏预计的关键影响因素。
3)装备抗损坏能力,反映装备抵抗损坏能力与装备损坏程度的反相关关系。一是装备的防护能力,即地形掩体防护、装甲防护、电磁防护等自我保护的抵抗打击能力,一般以防护能力系数量化;二是机动能力,即装备准备速度、快速转移、克服地形障碍的能力,转移一般以机动能力系数量化;三是伪装反侦察能力,即利用战场环境条件和装备自身特性的隐蔽伪装能力,一般以伪装能力系数量化。
2.2 面向维修保障的装备损坏程度判定影响因素
特定战场条件下的装备损坏程度不仅与装备性能影响性紧密相关,而且要考虑修复所需人员、器材、时间等情况[6]。因此,面向维修保障的装备损坏程度预计,可确保损坏程度评定的科学性和可行性。从装备损坏影响性、维修实施质效性、维修需求匹配性和维修所需时间4个层面逐个分析装备损坏程度的影响因素。
1)装备性能影响性,反映的是功能-效能劣化程度。装备在战场的价值在于发挥体系对抗条件下的作战效能。判定损坏影响性时,应基于战斗力生成角度考虑,其装备战斗力指数是评价损坏程度的重要指标。装备损坏的直接影响是装备部分功能劣化,根本影响时丧失相应的装备作战效能。一是装备核心功能完整度,主要考虑损坏的是否为核心或关键部件,其损坏影响装备核心功能的严重程度是重要的考量指标;二是装备作战效能完整度,主要考虑由装备核心功能劣化影响作战技术性能弱化最终导致的装备作战效能降低程度。
2)维修实施质效性,反映的是装备损坏后的可修复性。一是装备修复难易度,即“容不容易”的问题,主要指装备检测、诊断损坏的复杂性和困难度,维修技术操作的难易程度、成功率等;二是装备修复费效比,即“值不值得”的问题,主要指投入与产出的横向对比,也就是在特定修复标准及要求的前提下,修复装备所需的保障资源价值和修后装备战斗力恢复价值的综合考量。
3)维修需求匹配性,反映的是装备维修需求和能力的匹配性。一是维修资源的匹配性,基于器材、设备等维修资源是否容易携带、从阵地到后方考虑配备的维修资源能否满足维修需求,考虑现场还是后送维修,从而判定装备损坏程度。二是维修地点的便宜性,分析损坏地域是否适宜维修作业,是否便于后送修复,从而判定装备损坏程度。
4)维修所需时间,反映的是战时装备维修的允许时间。将维修装备时间区别于其他装备维修资源,主要考虑到战时装备维修的时间紧迫性,其维修装备的时间要求是判定装备损坏程度的关键指标。各个损坏程度对应的装备维修时间限度,既是装备维修任务量的直观体现,也是充分考虑了指定作战任务维修作业的战术要求。业界普遍认同检维修装备所需时间作为装备损坏程度的界定标准,并拟合装备损坏数量关于维修所需时间的分布函数,根据经验统计设定各损坏程度的维修所需时间上限,即可求得各损坏程度的装备数量比例。
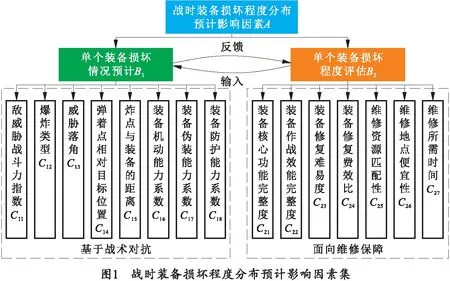
综上,构建战时装备损坏程度分布预计影响因素集如图1所示。
3 基于D-S的装备损坏分布预计
笔者基于战时装备损坏分布预计的影响因素考量,运用D-S证据理论和影响因素加权的方法,对战时装备损坏分布预计展开研究。
3.1 现有战时装备损坏程度分布预计方法分析
基于战术对抗的单个装备损坏程度判定及预计相关研究较多[7-8],而对于战时装备损坏程度分布的预计方法却鲜有论述,主要是基于维修时间或维修工作量分布的损坏程度分布和基于不确定性推理的损坏程度分布等。
理想情况下,基于维修时间的装备各损坏程度分布遵循正态分布、指数分布等规律,其应用条件如表2所示[9]。

表2 常见的基于维修时间的损坏程度分布函数
石文华等[10]将各损坏程度对应的修理时间区间上下限代入维修时间分布函数,求得装甲装备各损坏程度的分布比例。宋明昌等[11]按照维修机构对应的修理工作量范围求得损坏装备进入各维修机构的概率,以此对应各装备损坏程度的分布比例。伊洪冰等[3]参照俄军Эpланга模型可求解粗略的装备损坏程度分布。陈春良等[12]提出基于AHP-Bayes和Bootstrap方法对小样本数据统计分析,判定最相近的概率分布并构建维修工作量统计模型。但总体来说存在两方面局限性:一是依据维修时间的分布函数求解装备损坏程度分布时,各维修时间分布函数适用条件存在交叉,难以根据维修作业实际判定其维修时间分布类型;确定其分布类型和参数需要大量的先验数据,即使明确分布类型,其对应参数的求解仍是难题[13],实用性不强;基于维修时间的损坏程度分布忽略战场诸多因素影响,且对各损坏程度的维修时间区间依赖性较强。
常见的不确定推理方法有3类:基于D-S证据理论的证据推理、模糊推理和主观贝叶斯等概率推理,分别解决“分不清”或“不知道”多义情况、概念边界和内涵不明确以及随机事件发生概率的不确定性问题[14]。池斌等[15]充分运用D-S证据理论在信息融合和不确定性信息推理的优势,综合多个权威专家的损坏分布意见,采取Dempster合成规则求得新型军械装备传统的4种损坏程度比例的评估值,但没有给出装备损坏程度分布的具体分析。笔者在此基础上,忽略单装的基于战术对抗的影响因素,重点从面向维修保障的不同影响因素层面,分别考量融合专家对于损坏分布的预计数据,最终按各因素的影响权重求得装备6种损坏程度比例。
3.2 D-S证据理论基本概念
D-S证据理论于1967年由Dempster提出,1976年由其学生发展完善的不确定性推断融合处理方法。其核心在于科学合理地表示不确定性的度量方法,目的在于降低不确定性,提高数据精度和置信度[16]。
3.2.1 识别框架
D-S证据理论基于有限且相互独立的集合进行研究,表示该不确定性事件所有可能发生的结果,该集合即识别框架U。
3.2.2 基本概率分配函数
识别框架U所有子集的集合为U的幂集,记为2U,若集函数m:2U→[0,1]满足:
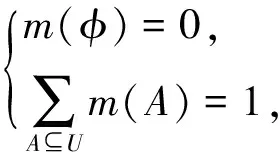
(1)
式中,m为U上的基本概率分配函数,也称mass函数,其基本概率分配值指证据对命题A为真的可信度,是D-S解决问题的关键。
3.2.3 信度函数和似真函数
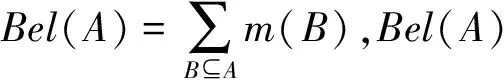
3.2.4 证据合成规则
∀A⊆U,m1、m2、…、mn为识别框架U上mass函数,则该n个mass函数的Dempster证据合成法则为
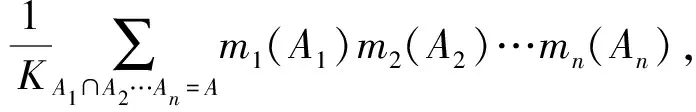
(2)
式中,归一化常数K为证据融合时的证据间的冲突程度。
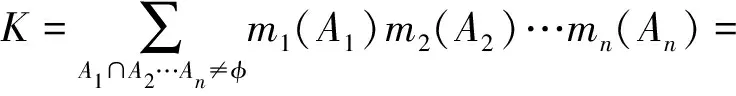
(3)
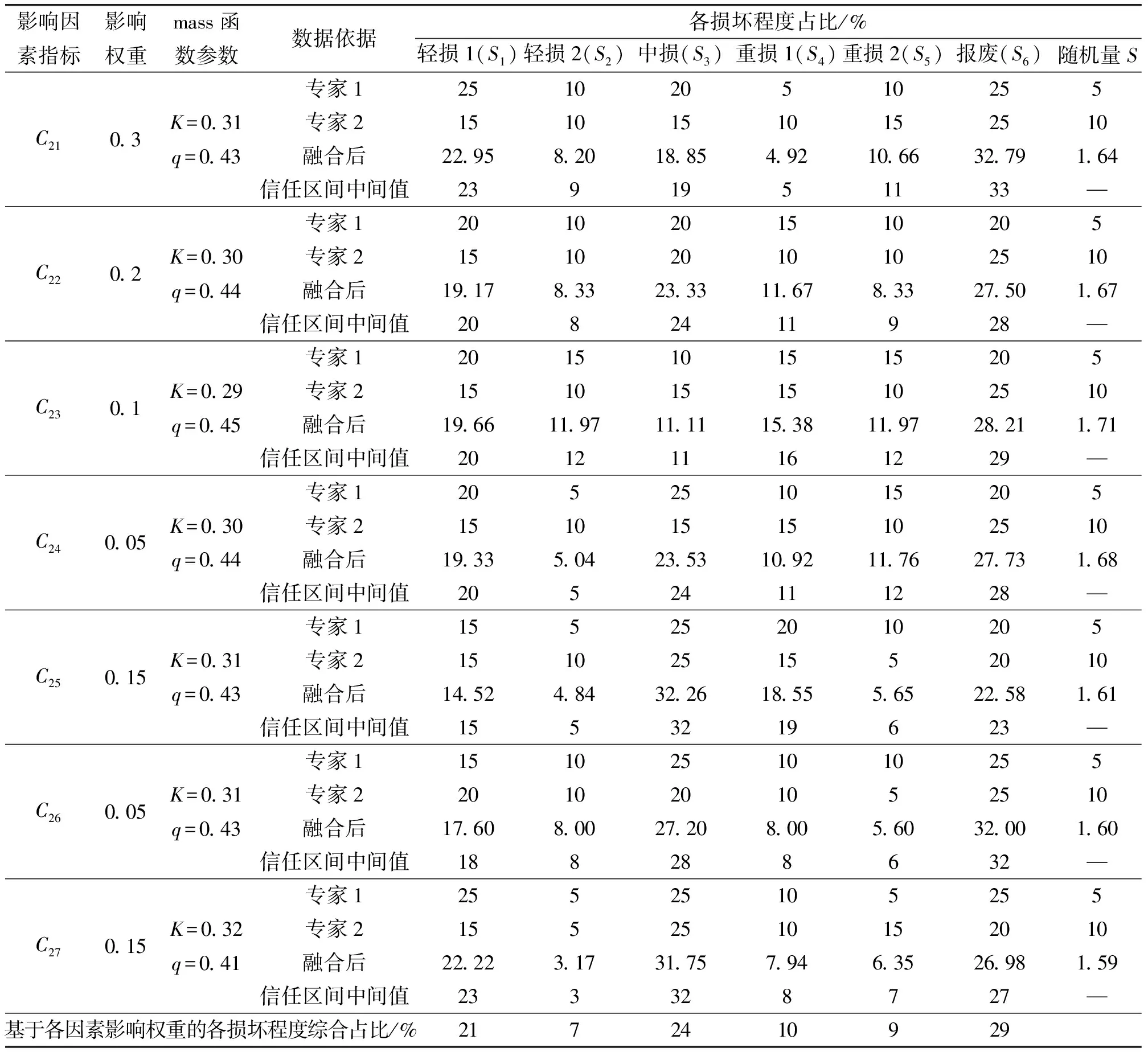
一般认为,当0 此外,设定模糊量q为表征证据合成的有效性和可靠性的参数: (4) 式中,常数ε为控制专家意见有效的界限,一般取值0.1~0.3,模糊量q大于0.4时,专家评判才有效[15]。 综合考虑装备损坏程度影响因素,区分装备特性划定各损坏程度评分标准。以某炮兵分队装备XX型榴弹炮、XX型火箭炮和XX型反坦克导弹为研究对象进行装备损坏程度的分布预测。前期运用德尔菲法,通过邀请专家打分得出相关因素对装备损坏程度分布的权重,即因素C21~C27对装备损坏程度分布的影响权重依次为0.30、0.20、0.10、0.05、0.15、0.05、0.15。基于装甲等装备各自损坏分布比例的基础数据,遴选2位相关领域的资深专家分别基于因素C21~C27对装备损坏分布比例作修正预测。以装备核心功能完整度C21为例分析其融合结果。2位专家对基于C21的装备损坏程度分布比例修正预测如表3所示。 表3 基于C21评定的装备损坏程度分布表 1)冲突系数K计算: 首先计算K0值: K0=m1(S1)×[m2(S2)+m2(S3)+…+m2(S6)])+ 进而可求得K=1-K0=0.305。 2)修正预测证据验证: 取ε=0.2,则求得模糊量为 由于q>0.4,认定本次预测证据有效可靠。 3)不同损坏程度的mass函数组合计算: 轻损1级的组合mass函数为 同理,可得其他损坏程度的组合mass函数分别为 随机量S的组合mass函数为 (m1⊕m2)(S)=0.016 4. 由此可求得基于影响因素C21对装备各损坏程度占比的信任区间,将信任区间的中间值作为相应损坏程度的预测比例。 因此,可分别基于影响因素C22~C27考量形成专家意见,运用D-S方法综合求得装备损坏程度分布比例。最终根据各因素的影响加权比例权重求得各损坏程度综合占比。其计算内容和结果如表4所示。 综上所述,该炮兵分队战时3种装备损坏程度占比分别为:轻损1级21%,轻损2级7%,中损24%,重损1级10%,重损2级9%,报废29%。与各个专家给出的损坏程度分布情况相比,此结果更贴近于战时装备各损坏程度占比的数据统计,既与传统的损坏程度分布经验数据大致相符,又体现了现代战争形势下装备损坏程度分布由轻损、重损向重损、报废倾斜的发展趋势。就本质而言,该方法兼顾了各专家对装备损坏系统分析和战场情况整体把握的综合判断,也减小了完全主观造成的随机因素偏差,以此方法研究战时装备损坏程度分布是科学可行的。 依据具体的装备各损坏程度占比情况,可更有针对性地进行战时装备维修保障的整体筹划和实施,有利于战时装备维修保障任务分工和维修资源的配置优化。 表4 基于各因素影响权重的损坏程度综合占比数据表 针对战时装备损坏程度分布预测问题,笔者从装备损坏程度分布的相关概念出发,基于战术对抗、面向维修保障分析了装备损坏程度分布的影响因素,分别从面向维修保障的各影响因素考虑,运用D-S证据理论将相关领域专家作出的损坏程度分布预测结果融合,最终按各因素影响权重综合求得各损坏程度比例,一定程度上提高了装备损坏程度分布的科学性和可信度。然而,笔者仅针对专家给出装备损坏分布的结果进行主观上修正和融合,下一步可基于仿真虚拟对抗、人工智能的损坏程度统计推算方法进行分布预测的系统研究。3.3 战时装备损坏分布预计
m1(S2)×[m2(S1)+m2(S3)+…+m2(S6)]+
m1(S3)×[m2(S1)+m2(S2)+m2(S4)+…+
m2(S6)]+m1(S4)×[m2(S1)+…+m2(S3)+
m2(S5)+m2(S6)]+m1(S5)×[m2(S1)+…+
m2(S4)+m2(S6)]+m1(S6)×[m2(S1)+
…+m2(S5)]=0.695,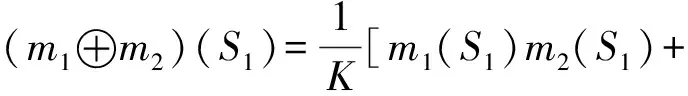
4 结束语
