海洋立管浮力装置抗滑脱力的数值评估方法

张祥,相政乐,张启发,赵利,王铭浩,徐瑞,陈东阳

(1.海油发展珠海管道工程有限公司,广东 珠海 519050;2.扬州大学 电气与能源动力工程学院,江苏 扬州 225100;3.西北工业大学 海洋研究院,江苏 苏州 215000)

关于海洋立管浮力装置的抗滑脱力计算,缺乏数值评估方法,国内外标准规范中没有直接可以参考的数据,通常国际上浮力装置制造商均按照浮力装置设计净浮力的4倍进行估算。浮力装置通过管卡模块安装在立管上,评估其抗滑脱力,主要包含两种工况:①立管安装下水阶段,此时需重点分析浮力装置入水时,波浪对浮力装置的砰击力,以确保浮力装置能够稳固地固定在立管上,不发生滑移或滑脱;②立管安装就位后的服役运行阶段,立管及浮力装置受浮体平台(如FPSO)运动、风浪流荷载等的作用,尤其大的风浪、洋流以及剧烈的FPSO运动等条件下,浮力装置与立管之间不能发生滑移,以保证立管能够按照原始设计的波型稳定工作[1]。

考虑通过安装和服役两种工况下的海洋立管浮力装置数值分析,探讨海洋立管浮力装置抗滑脱力的数值评估方法,为海洋立管浮力装置的设计、试验提供数值支撑。

1 安装阶段浮力装置的抗滑脱力

1.1 计算模型

作用在物体上的力,对静止水体,物体的砰击力可表达为

(1)

式中:Cs为砰击力系数;ρ为水的密度;Ap为物体与水面的投影面积;vs为物体的入水速度。

当物体在波浪中入水时,考虑物体与波浪面的相对速度,这时,砰击力可表达为

(2)

砰击力跟砰击力系数密切相关,根据DNV-RP-C205以及DNV-RP-H103,对于圆柱体,砰击力系数取为3。

以12 in立管为例。当浮力装置安装到立管上,随立管一起入水时,浮力装置将受到重力、浮力、波浪水面起伏引起的惯性力与黏性力及波浪砰击力。此外,立管与浮力装置随安装船起伏运动,自身也会引起一定的惯性力。因此,需同时考虑所有的力,以确定浮力装置所需紧固力的最大值。

采用OrcaFlex软件对浮力装置在安装入水时的受力进行分析[2-4],相关假设如下。

1)安装船模型。采用OrcaFlex软件自带的船舶模型,长103 m,宽16 m,吃水6.7 m,排水量10 000 t。水动力参数参见OrcaFlex软件手册。

2)浮力装置模型。如图1所示,浮力装置通过管卡模块安装固定在立管上。

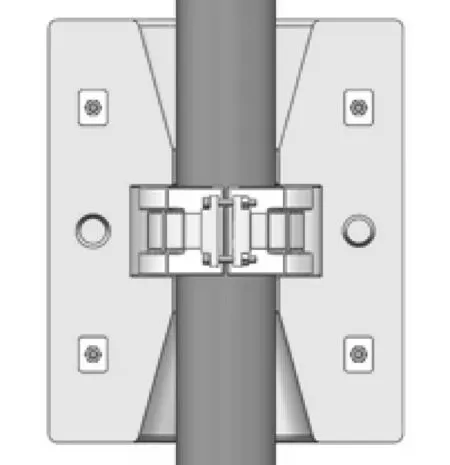
图1 浮力装置模型剖面示意

浮力装置几何重量特征见表1。

表1 浮力装置几何重量特性

浮力装置水动力系数选取见表2。

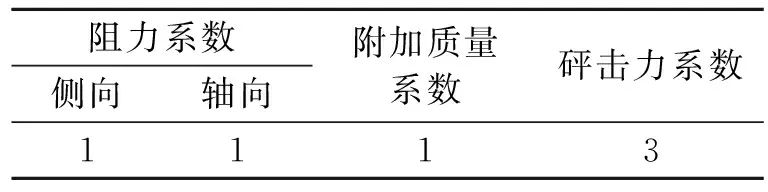
表2 浮力装置水动力系数特性

3)安装浮力装置的立管与安装船的连接模型。在充分考虑安装实际工况下,为简化模型,假设采用一段带浮力装置的刚性立管直接与安装船相连接,且考虑立管与安装船分别垂直、呈45°、平行3种相对位置,见图2。

图2 安装浮力装置的立管与安装船的相对位置示意

针对以上每种相对位置,再分别考虑浮力装置中心点距离水面1、0、-1、-2 m四种情况,即总共考察12组工况条件下浮力装置的受力情况。

4)立管安装的海况参数。考虑安装海况为:5级海况,Hs=2.5 m,Tz=5 s,流速1.5 m/s,考虑波浪为迎浪情况(此时安装船纵摇较严重)。

1.2 抗滑脱力结果分析

对假设的安装海况下,12组工况条件进行分析,立管与安装船垂直且浮力装置中心点距离水面0 m时,即垂直&0 m工况条件下,浮力装置所受竖向波浪砰击力时程示例、浮力装置所受水平向波浪砰击力时程示例及浮力装置所受沿立管轴向连接力时程示例见图3～5。浮力装置所受竖向砰击力、水平向砰击力以及轴向连接力的最大值见表3。

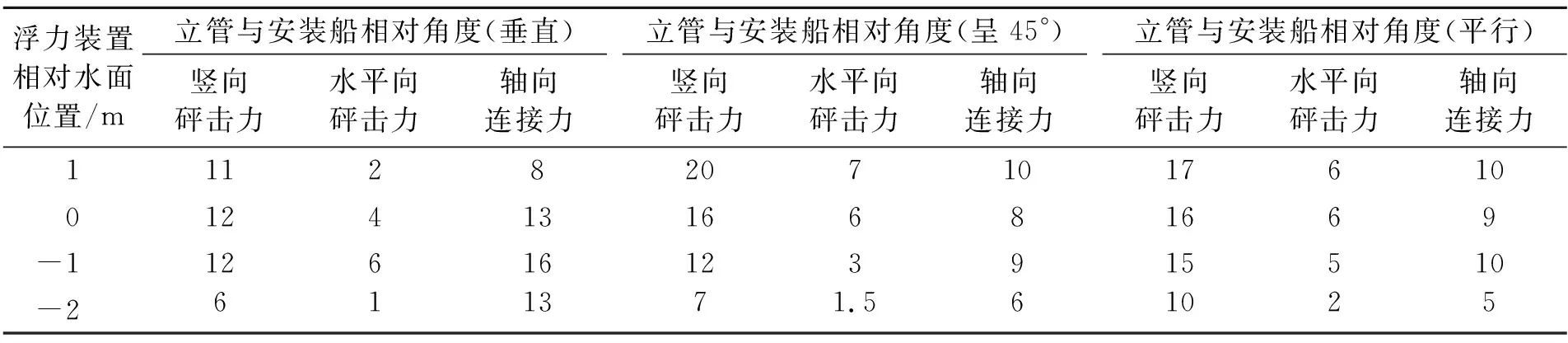
表3 12组工况条件下,浮力装置所受砰击力及轴向连接力最大值 kN

图3 浮力装置所受竖向砰击力时程示例

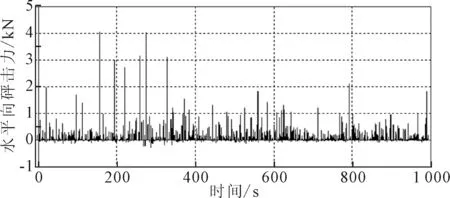
图4 浮力装置所受水平向砰击力时程示例

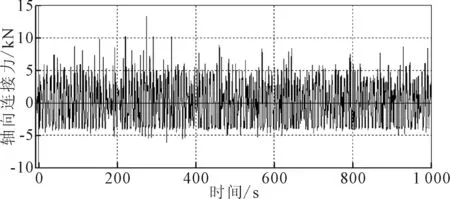
图5 浮力装置所受沿立管轴向连接力时程

可以看出,浮力装置沿立管轴向所受连接力最大为16 kN,意味着需要至少16 kN的紧固力,才能够保证在目前假设的安装工况下浮力装置安装下水时不发生滑脱。

2 服役阶段浮力装置的抗滑脱力

2.1 计算模型

以1 500 m水深、懒波型立管为例,将浮力装置安装固定在立管上,采用OrcaFlex软件,对一定的极限服役条件下,浮力装置所受的紧固力值进行模拟分析。相关假设如下。

1)FPSO船舶模型。FPSO模型长250 m,宽40 m,吃水17 m,排水量150 000 t。该船模型由OrcaFlex软件自带103 m船按等比尺放大2.5倍得到,其水动力特性参见OrcaFlex软件手册。

2)浮力装置模型。浮力装置模型和1.1节中的浮力装置模型一致,其特性见表1、2。

3)立管特性。以12 in柔性立管为例,考察安装浮力装置的立管在一定的极限海况下浮力装置所需紧固力值,该立管基本特性见表4。

表4 12 in柔性立管参数特性

4)立管线型设计。立管与FPSO连接点位于船底中心,往船艏方向70 m中心线上,离开角12°,立管海底锚固点距离FPSO中心水平距离1 700 m,立管总长2 800 m。其中,立管从FPSO向下伸出的第一段光管段长800 m,中间安装浮力装置段长500 m,连接海底光管段长1 500 m。FPSO处于平衡位置时立管的波型见图6。

图6 FPSO平衡位置时,立管的几何特征

其中,FPSO处于平衡位置时,立管第一段底部最低点距离泥面1 010 m,中间安装浮力装置段立管顶部距离海平面390 m,卧泥段长500 m,这样的布置形式既可以保证立管不受海面船舶的影响,同时又能够减轻立管底部触泥点位置的受力。

2.2 抗滑脱力结果分析

2.2.1 静力分析

考虑1 500 m水深的8%,即120 m作为FPSO最大水平偏移量,考察FPSO最远偏移时立管的最大张力值。结果表明:采用选定的浮力装置布置数量和形式,立管的最大张力为300 kN(小于1 500 kN),可以保证在FPSO最远端位移值时,满足立管安全要求。见图7、8。

图7 FPSO最远端位移时,立管几何特征

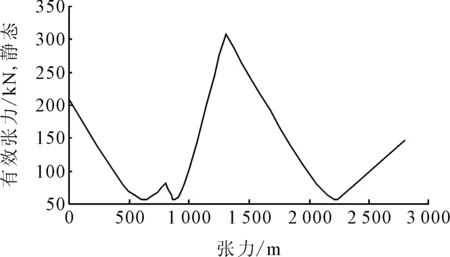
图8 FPSO最远端位移时,立管全管段最大张力值

此外,分析FPSO最近偏移时立管的最小弯曲半径值,结果表明,采用选定的浮力装置布置数量和形式,立管最小弯曲半径为50 m(大于10 m的MBR要求),可以保证在FPSO最近端位移值时,立管的最小弯曲半径满足安全要求。见图9、10。

图9 FPSO最近端位移时,立管的几何特征

图10 FPSO最近端位移时,立管全管段最小弯曲半径值

对安装浮力装置假设模型的立管静力分析结果表明:上述模型中立管及浮力装置的布置形式,是一种较为合理的立管线型,能够满足立管的服役安全要求。

2.2.2 动力分析

假设极端服役海况如下:波浪Hs=12 m,Tz=12 s,流速1.5 m/s。FPSO在极端波浪作用下产生剧烈的波频运动,带动立管与浮力装置在水下振动。

在计算FPSO的运动响应时,分别取FPSO所处3种位置,分别考虑3种波浪对FPSO的攻角,即总共9种工况条件。

此外,考虑到浮力装置布置较多,采用分步式等效模型,仅在立管顶部布置12个离散型浮力装置,以便分析浮力装置的受力,模型见图6。

FPSO平衡位置及0°波浪攻角工况条件下,浮力装置沿立管轴向所受连接力,即浮力装置所需紧固力时程见图11。9组工况条件下浮力装置所受轴向连接力最大值见表5。

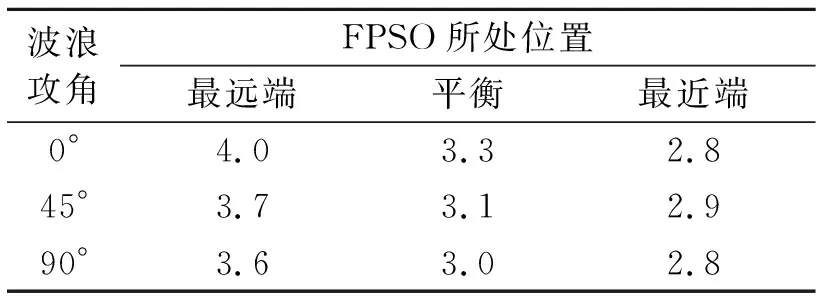
表5 9组工况条件下,浮力装置所;受轴向连接力最大值 kN

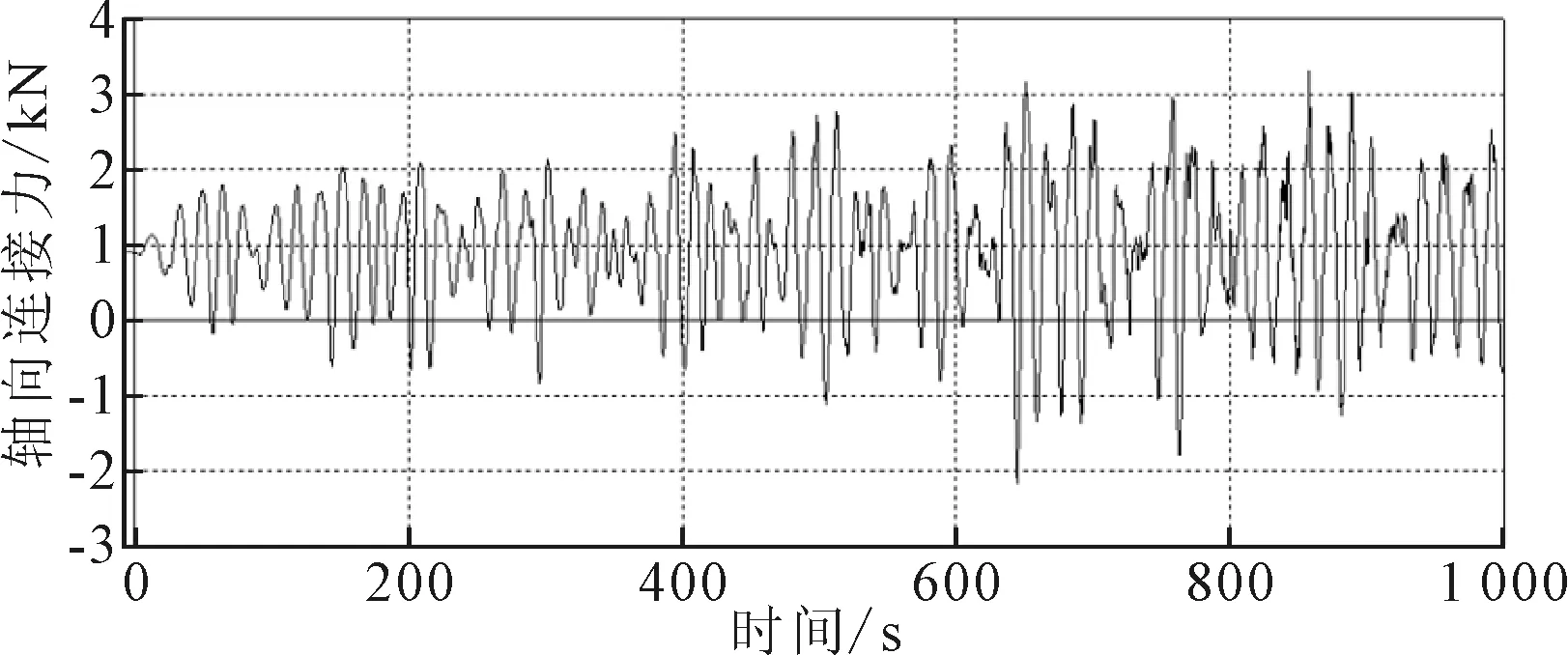
图11 浮力装置轴向连接力时程示例

安装浮力装置的立管动力分析结果表明,浮力装置所受轴向连接力最大为4 kN,即浮力装置与立管之间所需的紧固力最大为4 kN,意味着需要至少4 kN的紧固力,可保证在目前假设的服役工况下浮力装置服役运行时不发生滑脱。

3 结论

对于海洋立管浮力装置抗滑脱力的计算取值,安装工况为控制工况,需要特别注意;服役工况为非控制工况,可用于具体取值的校核。但对于实际的海洋立管浮力装置工程设计,还需针对具体的实际立管情况与服役海况条件等进行所需紧固力的验算。

所述浮力装置的设计净浮力为3.8 kN,浮力装置的抗滑脱力取值为16 kN,浮力装置抗滑脱力的取值是其设计净浮力的4.2倍。国际上浮力装置制造商一般都是按照浮力装置设计净浮力的4倍取值,仿真分析结果与此相吻合,也佐证了本文数值方法的合理性。