软钢臂式单点系泊系统运动性能优化
2023-04-27李牧刘诗学李鹏齐晓亮刘剑楠李恬恬
李牧,刘诗学,李鹏,齐晓亮,刘剑楠,李恬恬
(中海油能源发展股份有限公司采油服务分公司,天津 300452)
软钢臂式单点系泊系统运动性能对于FPSO运营生产安全至关重要,学者针对软钢臂系泊系统的运动受力,围绕其静态特性、动态特性在频域、时域开展了大量理论分析和模拟实验研究[1-4]。在FPSO运营中,软钢臂结构在实际海况中的运动特性会对软钢臂结构铰接点可靠性以及系泊腿受力产生影响[5]。为此,针对软钢臂单点系泊软钢臂结构的运动特性,对双软钢臂结构软钢臂单点系泊FPSO进行分析,以渤海某FPSO为研究对象,建立FPSO水动力模型和系泊系统模型,根据实测数据分析不同海况下软钢臂结构运动特性,并针对其运动特性提出优化方案。
1 计算理论
1.1 计算流程
对渤海某FPSO通过调载的方式进行系泊系统运动响应优化分析。首先,在水动力软件AQWA中建立FPSO船体水动力模型,运用AQWA-LINE模块计算FPSO波浪力、附加质量、附加阻尼。其次,在系泊分析软件Orcaflex中建立FPSO系泊模型,将AQWA-LINE结果中的幅值响应算子、辐射阻尼等数据输入到Orcaflex软件中,计算风浪流联合作用下FPSO受力及运动情况。
1.2 理论方法
AQWA基于三维势流理论,不考虑粘性,假设流体为不可压缩理想流体,用势函数表示整个流体,根据拉普拉斯方程求出速度势[6],由拉格朗日方程、伯努利方程及其积分、运动方程,求解出船体在单位波幅的规则波下的幅值响应算子。Orcaflex动力分析软件在时域内求解系泊系统整体运动方程,对FPSO船体及系泊系统进行全耦合分析,得到时域内系统的运动和受力。
2 FPSO建模及验证
2.1 FPSO船体模型
FPSO船体主尺度见表1,根据船体型值表建模,由吃水划分水线面建立面元模型,见图1。共计划分3 278个节点、3 141个单元。
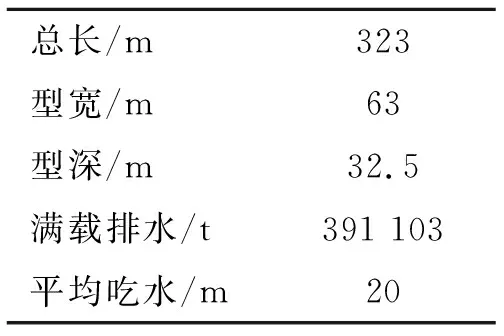
表1 FPSO船体主尺度
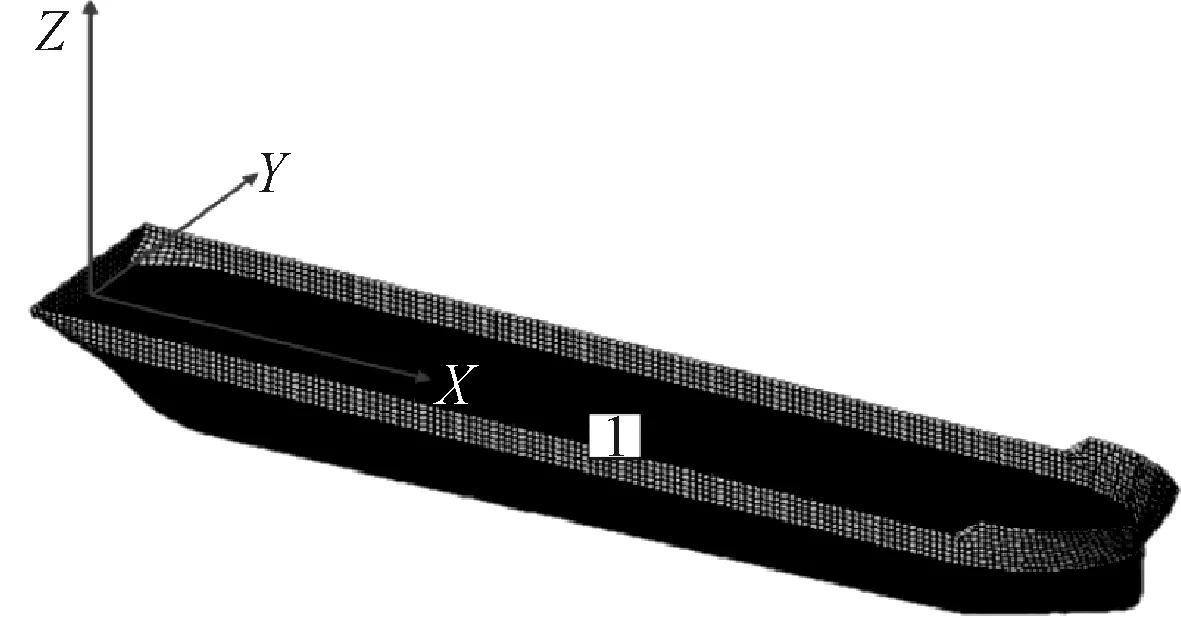
图1 FPSO面元模型
2.2 FPSO系泊模型
该FPSO采用水上双软钢臂系泊系统,系泊结构参数见表2,在Orcaflex软件中建立系泊模型,用6Dbouy来模拟软钢臂结构。

表2 软钢臂结构参数
2.3 FPSO系泊模型验证
对建立的系泊模型进行静态分析,计算系泊刚度并与设计值进行对比,绘制水平恢复力刚度曲线,见图2。设计值与模型计算值吻合良好,验证系泊模型的准确性。
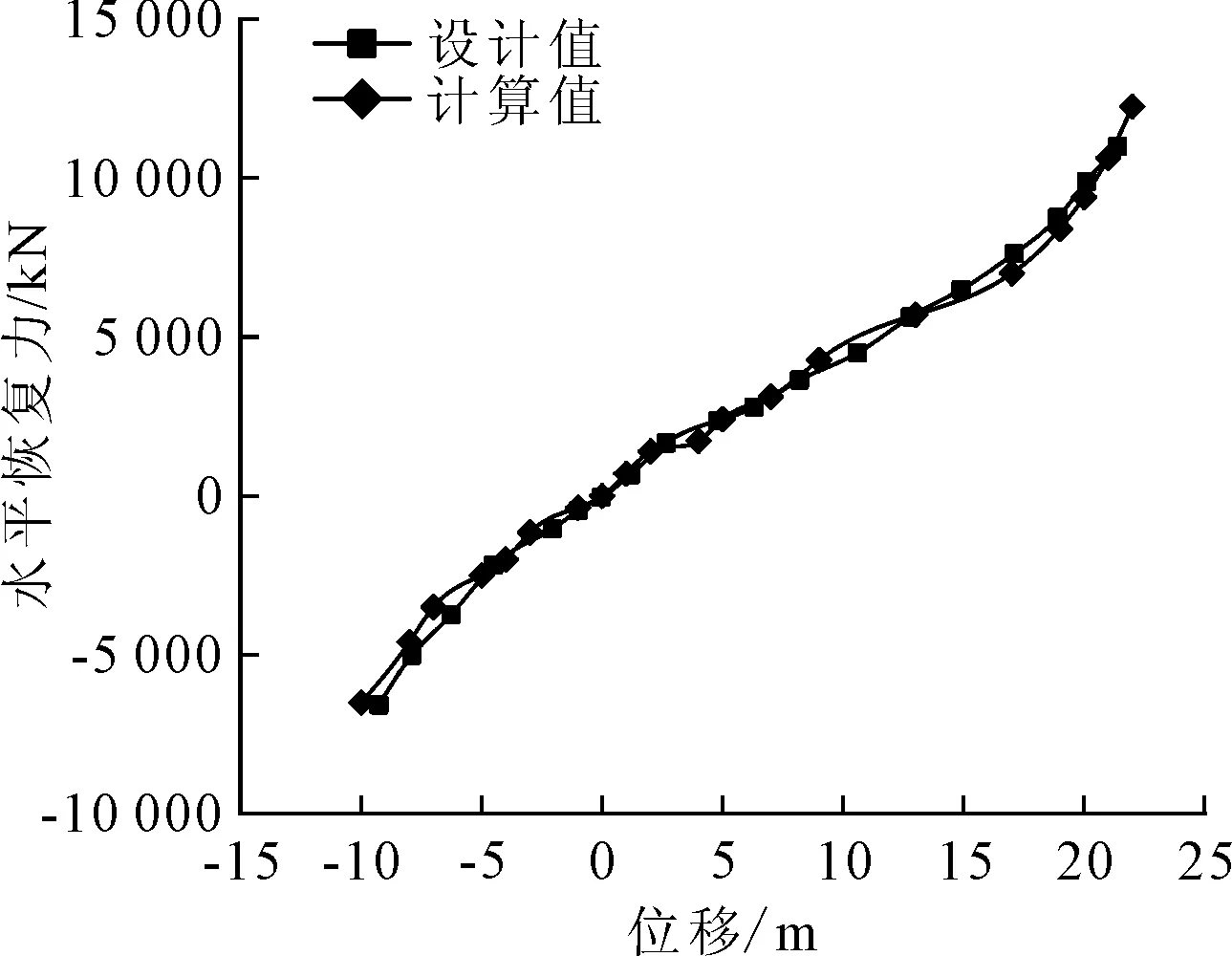
图2 系泊模型的刚度变化
3 软钢臂运动特性分析
在真实海况中,双软钢臂单点系泊系统的两个YOKE结构在外部环境载荷的作用下会绕连接杆旋转,见图3a),当双软钢臂的旋转角度θ1和θ2不等时,两软钢臂之间会形成高度差h。
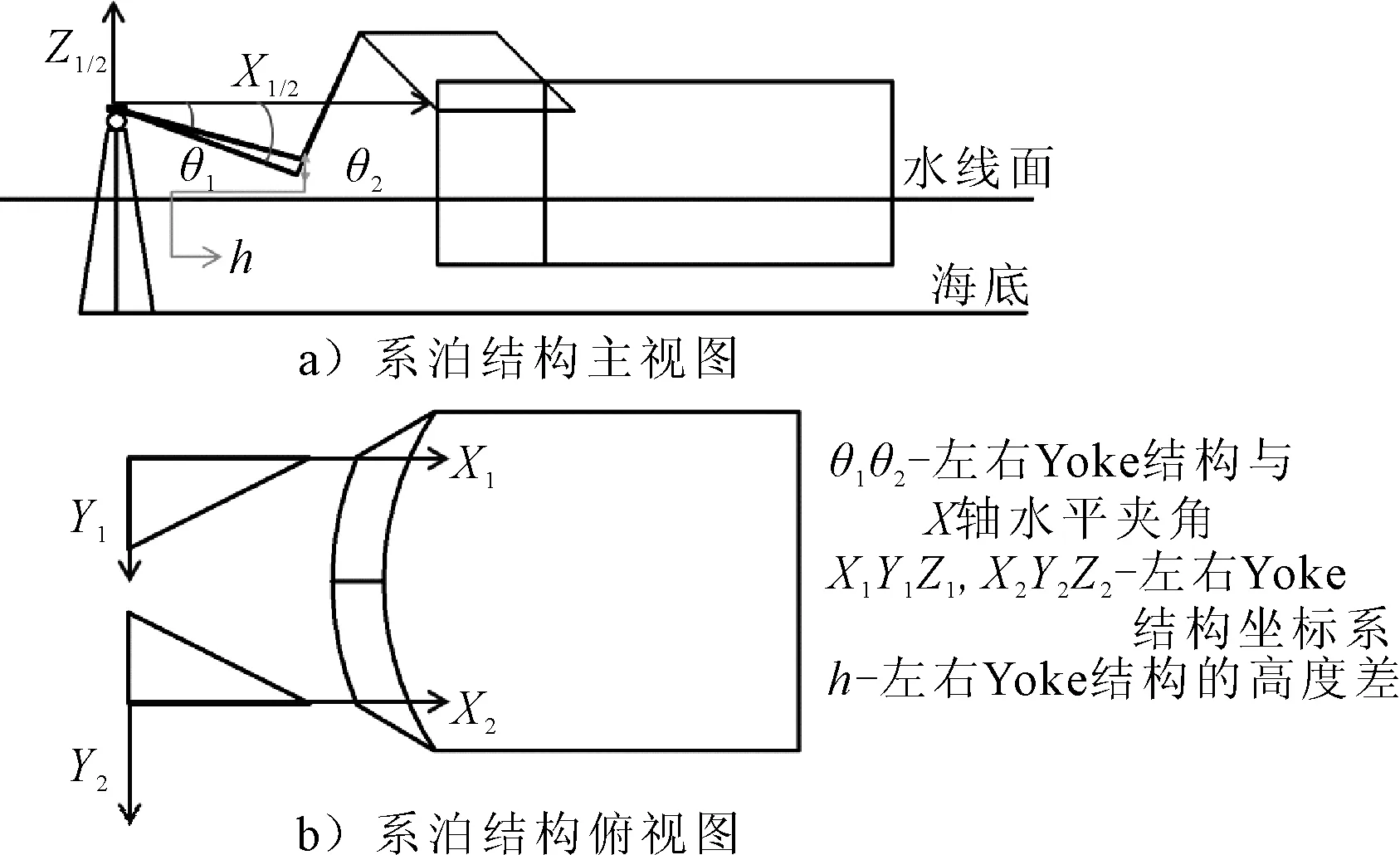
图3 双软钢臂系泊系统结构
h=l1sinθ1-l2sinθ2
(1)
式中:l1,l2为左右软钢臂长度。
为探究高度差产生的原因,对系泊模型进行时域模拟,模拟时间3 h,时间步长0.25 s,见表3、4。

表3 数值模拟环境载荷(一年一遇)
数值模拟工况按风浪同向、流向改变(工况1-4),风浪异向、流向改变(工况5-8)分为两组,分别分析其对双软钢臂高度差的影响。
3.1 风浪同向模拟
对工况1~4进行时域计算,从结果中提取软钢臂旋转角度θ1、θ2,计算旋转角度差值和高度差见图4(图中正值表示左侧大于右侧,负值表示右侧大于左侧),并统计差值的最大值、最小值、变化幅值,见表5。
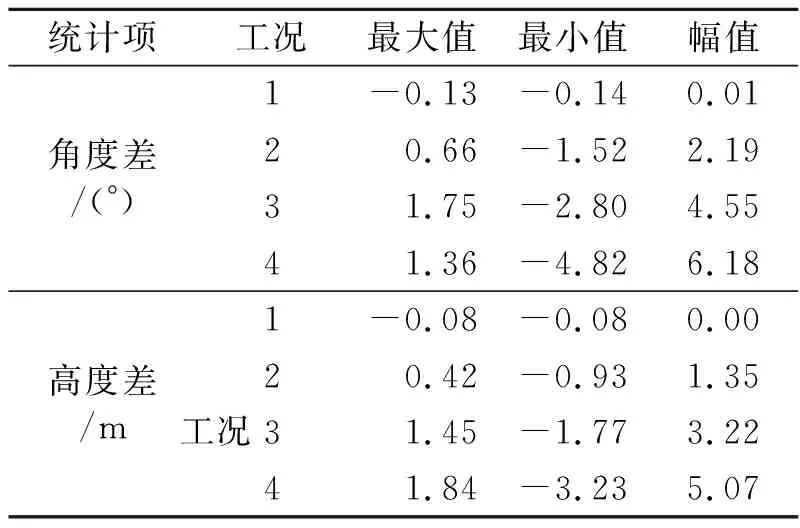
表5 工况1~4角度差及高度差统计值
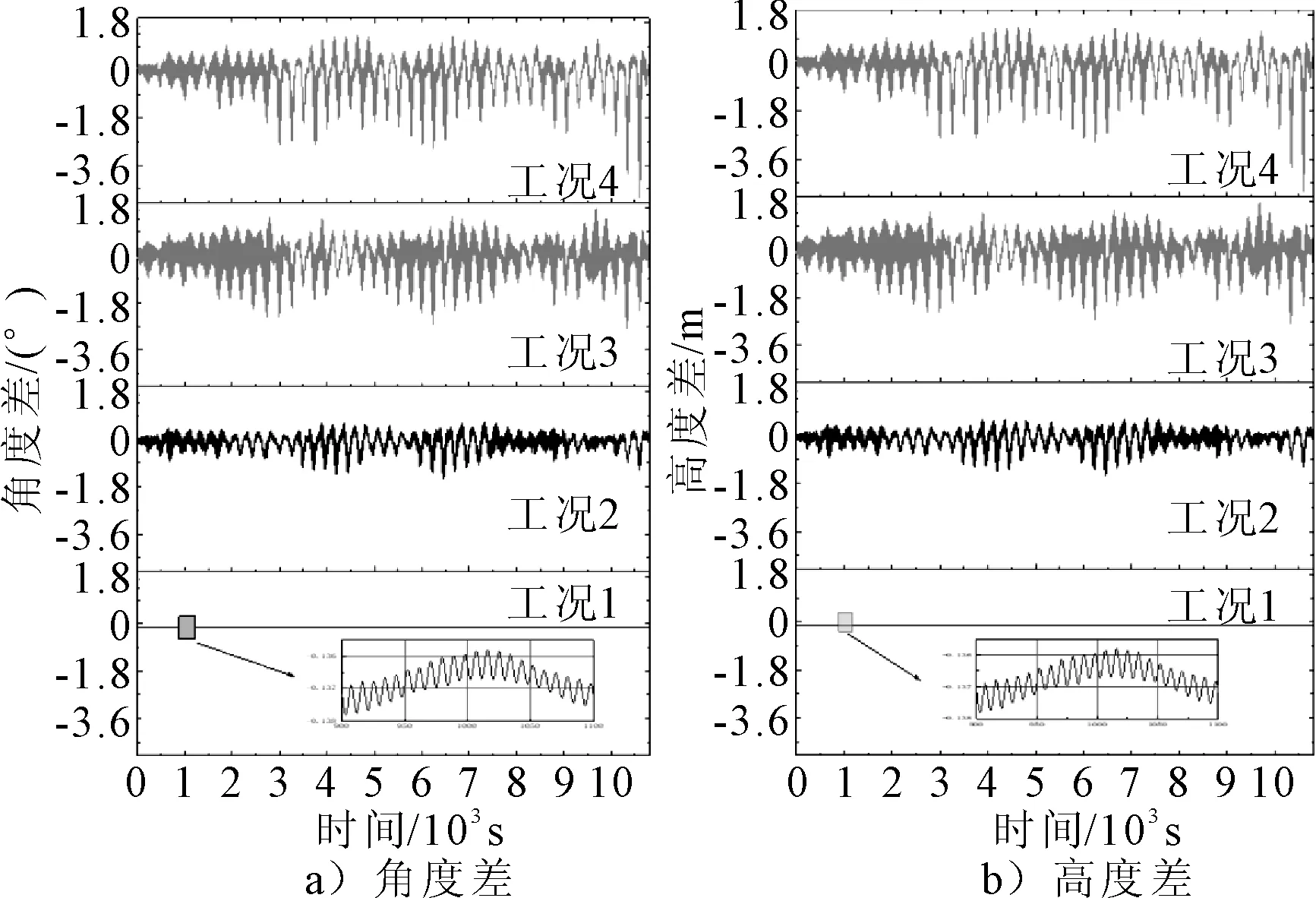
图4 工况1~4角度差及高度差对比
从图4可以看出,当风浪流同向时,双软钢臂几乎没有角度差和高度差,双软钢臂的高度差随角度差的变化而变化。从图4和表5可观察到,在风浪同向时,随流与浪向夹角的增加,双软钢臂角度差、高度差变大,差值的幅值变大。
3.2 风浪异向模拟
对工况5-8进行时域计算,并从结果中提取软钢臂旋转角度θ1、θ2,并计算旋转角度差值和高度差见图5,并统计差值的最大值、最小值、变化幅值,见表6。
从图5可以看出,双软钢臂的高度差随角度差的变化而变化,两者存在一定的相关性。同时,从图5和表6可观察到,在风浪同异向时,随流与浪向夹角的增加,双软钢臂角度差、高度差变大,差值的幅值变大。
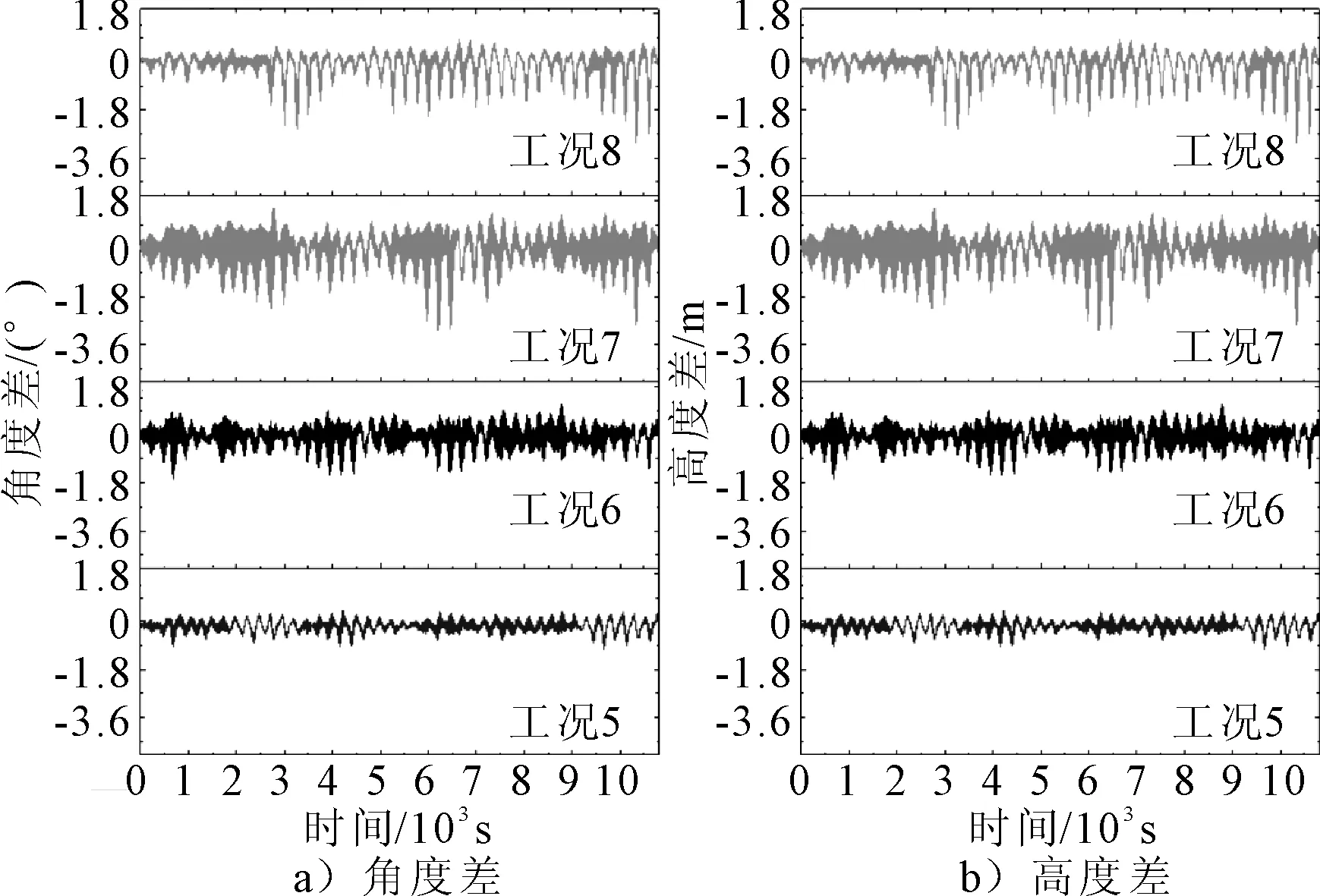
图5 工况5-8角度差及高度差对比
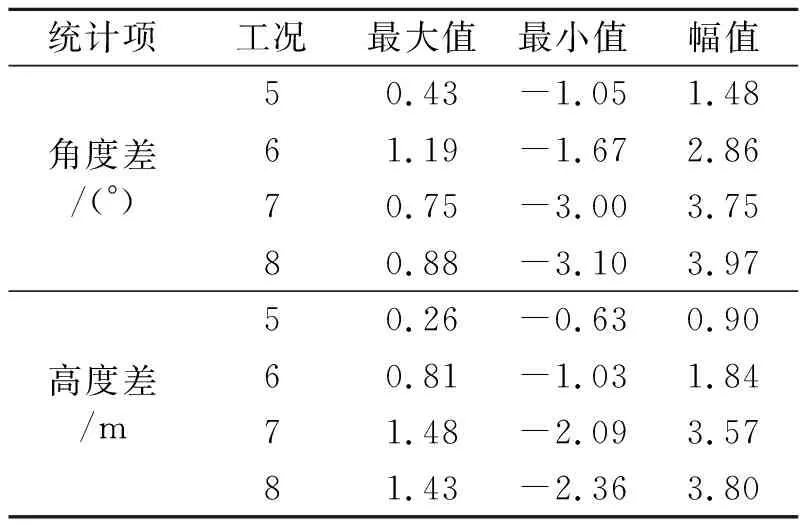
表6 工况5-8角度差及高度差统计值
对比可以看出,双软钢臂结构高度差和角度差是由于环境组合方向的差异导致,高度差随角度差的变化而变化。在风浪同向或异向时,随流与浪向夹角的增加,双软钢臂角度差、高度差变大,差值的幅值变大。
4 软钢臂运动优化
根据3.1节分析中可知,在工况4中,双软钢臂高度差的幅值达到6 m,这可能对系泊系统连接部件造成损伤,为降低双软钢臂结构的高度差,可以通过对软钢臂结构的压载箱位置进行调整,进而改变软钢臂结构的重心位置。如表7所示,重心位置的坐标相对于图3中所示坐标系,重心位置编号3是原始数值模拟时采用的压载重心位置,重心位置1~4、5~8、9~12分别从x,y,z三个方向进行优化。

表7 软钢臂压载重心位置优化
4.1 优化结果分析
重心位置1~12在上述工况8的环境载荷下进行3 h模拟,时间步长0.25 s,数值模拟角度差值和高度差见图6、7、8,差值的最大值、最小值、变化幅值见表8。
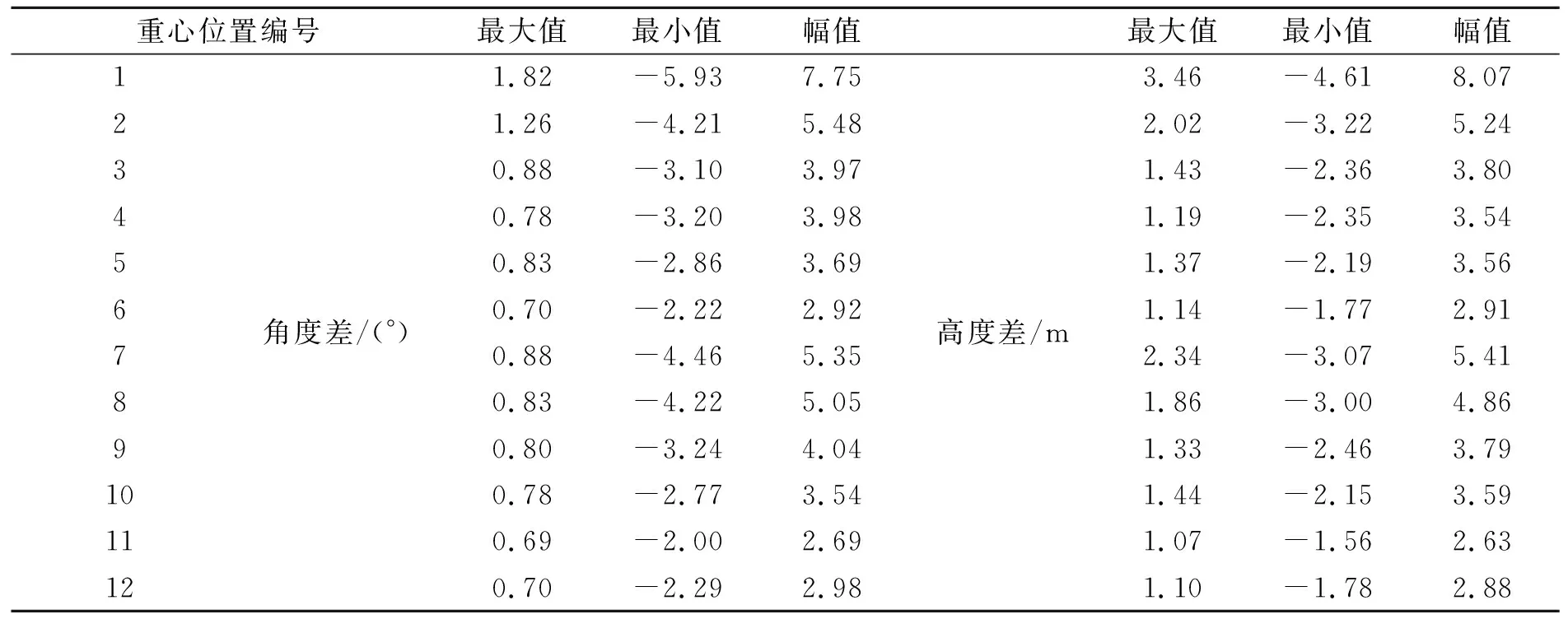
表8 重心位置1-12角度差及高度差统计值
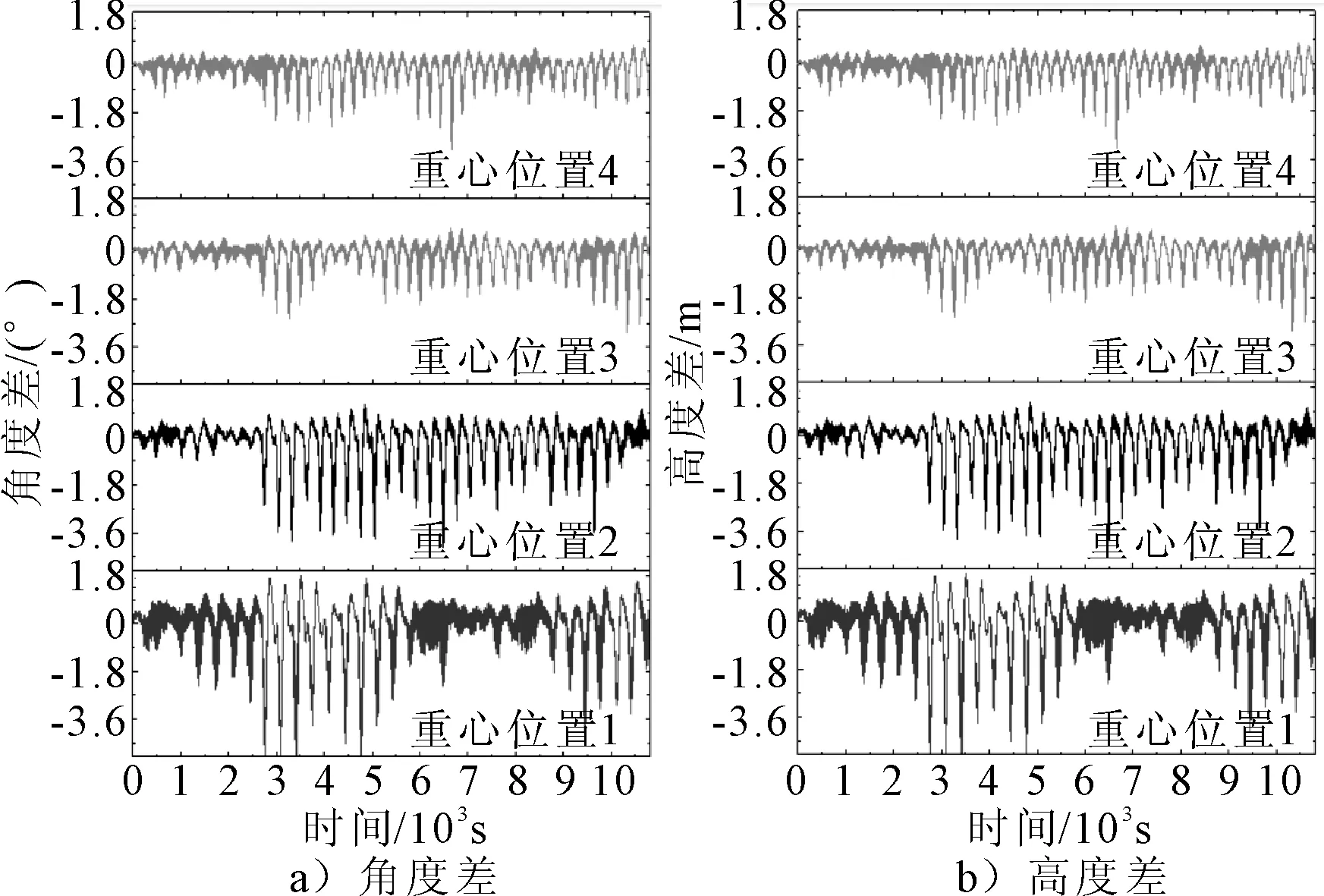
图6 重心位置1~4角度差及高度差对比
可以看出,双软钢臂结构角度差和高度差随重心位置在x向远离坐标原点而减小,随重心位置在y向相互靠近而减小,随重心位置在z向远离坐标原点先变小后边大,综合最优位置为重心位置11。
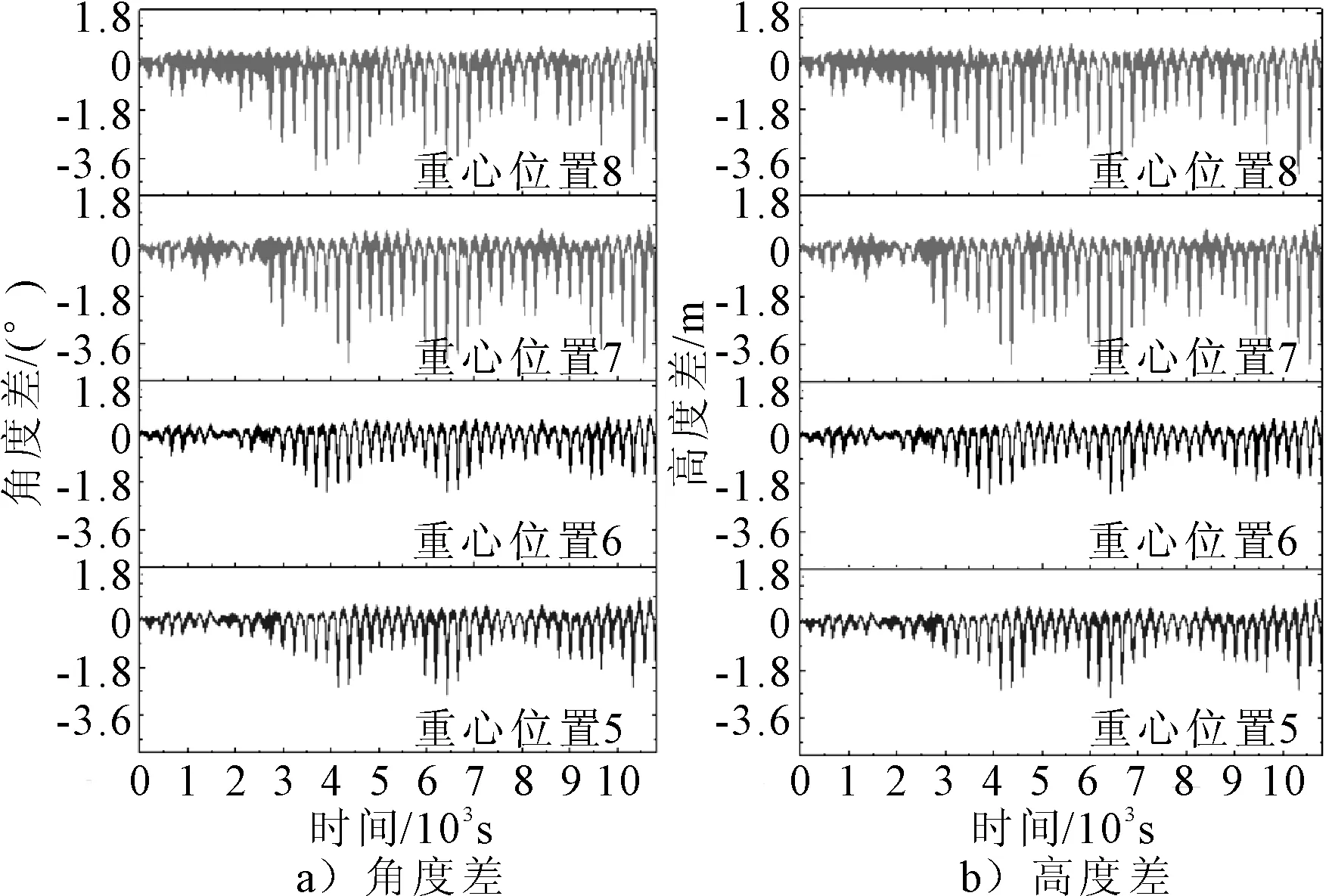
图7 重心位置5~8角度差及高度差对比
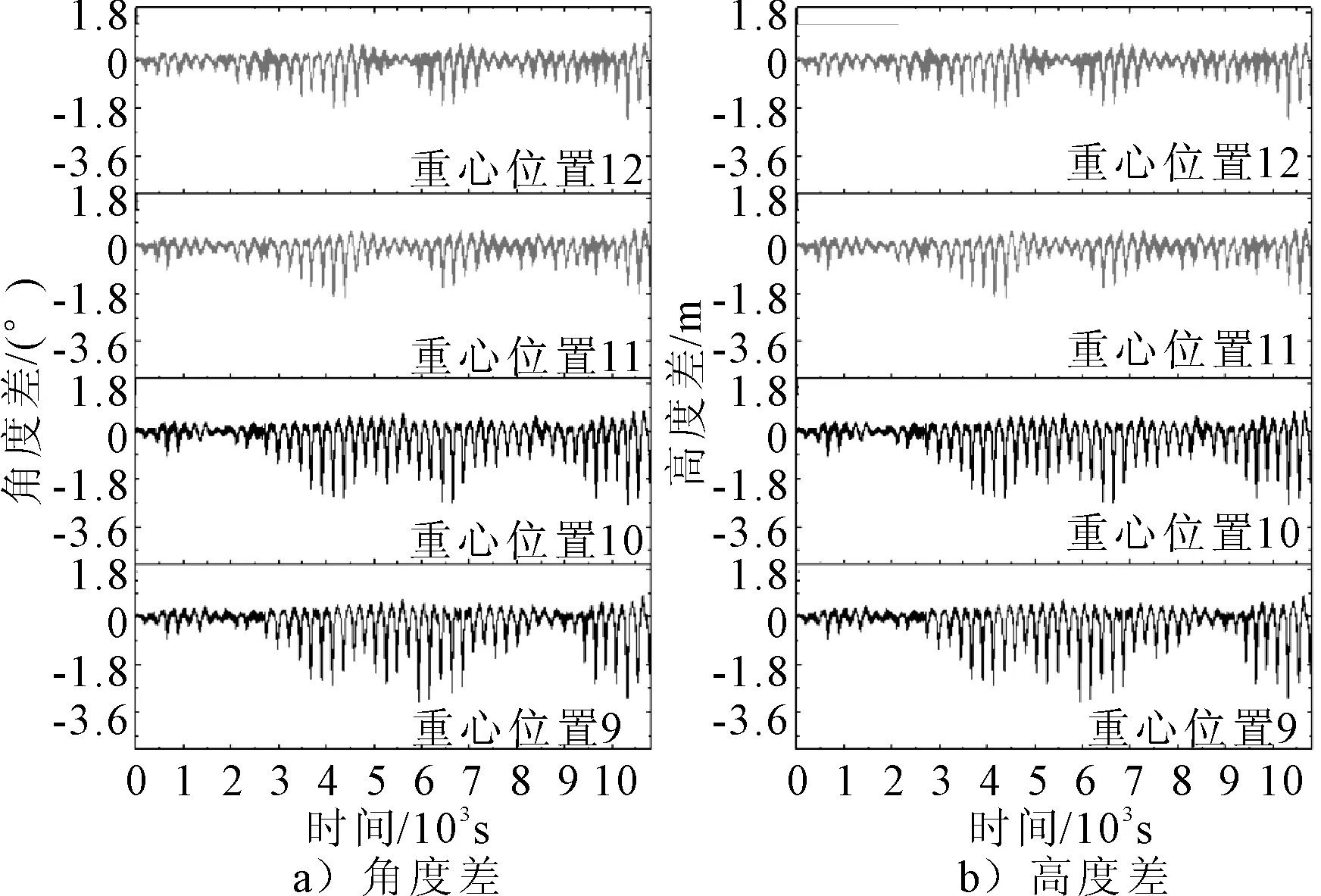
图8 重心位置9~12角度差及高度差对比
4.2 优化前后对比
取最优重心位置与未优化的重心位置对工况4进行模拟,比较两位置的角度差和高度差,结果见图9,统计差值的最大值、最小值、幅值见表9。从图9和表9可以看出,相对于系泊系统的初始状态,优化后的双软钢臂角度差和高度差变化都变小,运动幅值也缩小,说明通过调整系泊系统压载箱位置,改变软钢臂结构的重心位置可以有效优化双软钢臂的相对运动,降低两者之间的运动不协调性。
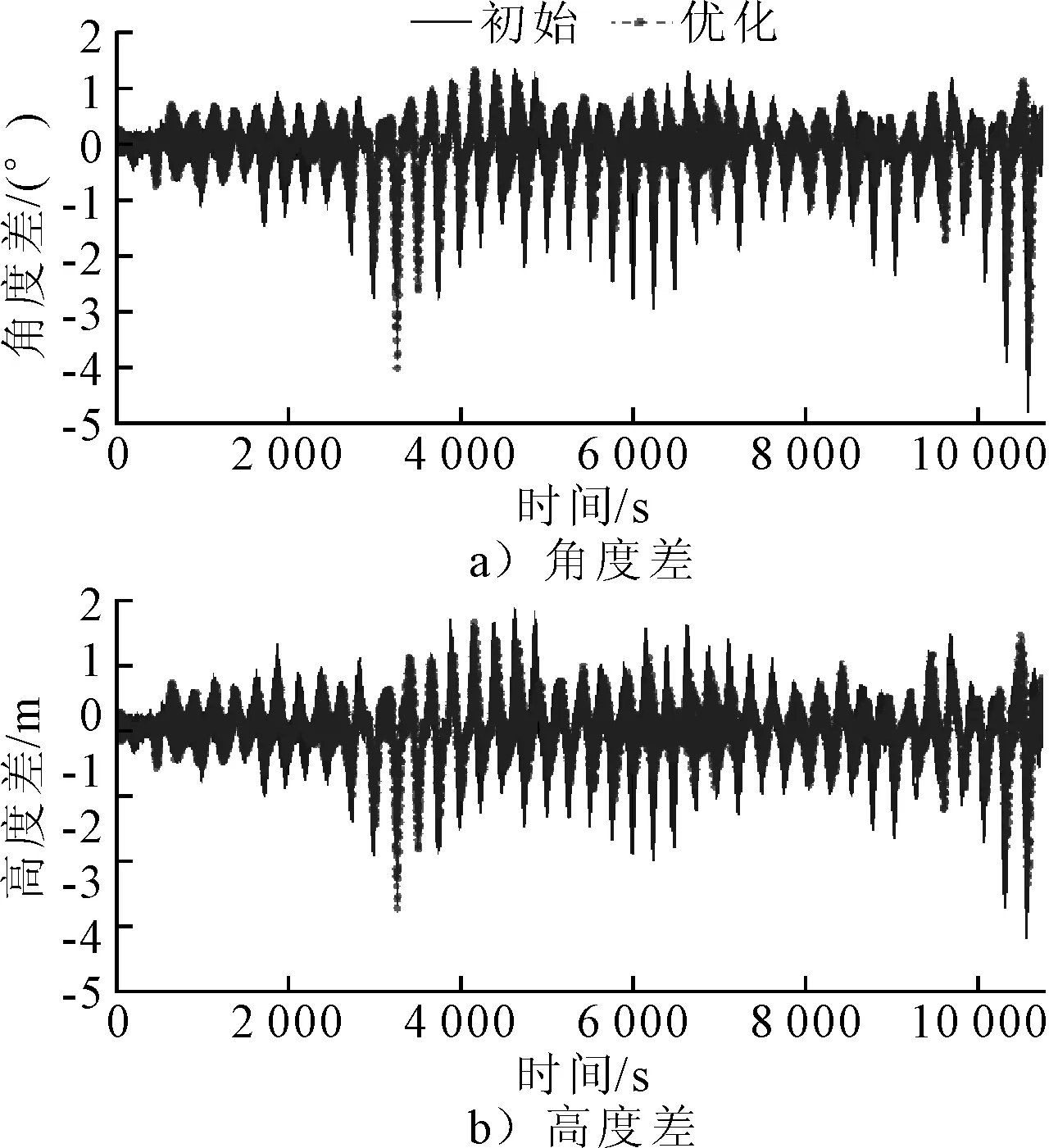
图9 重心位置优化前后插值对比
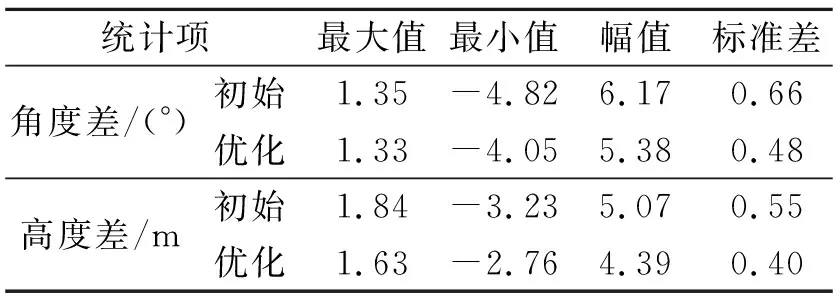
表9 优化前后角度差及高度差统计值
5 结论
在实际海况下,在水上双软刚臂系泊系统运行过程中,两软钢臂之间会存在高度差,存在运动不一致的情况,对系泊系统构件的稳定运行造成隐患,对软钢臂结构铰接点可靠性以及系泊腿受力产生影响。当风浪流同向时,双软钢臂角度和高度运动情况较为一致,当风浪流异向时,双软钢臂角度和高度运动情况存在较大差异,并且随着流向与浪向夹角的增加,双软钢臂角度差、高度差均变大。因此,通过调整压载箱位置来改变重心位置,可降低双软钢臂的角度差及高度差。该方法可以优化双软钢臂运动性能,为工程实际问题和海上作业人员提供参考。
