基于模拟退火与BEHHO算法的火力分配方案优化

李豇粼 张静骁 张凯博 白梅娟 侯帅

关键词：火力分配；混合算法；哈里斯鹰优化算法；模拟退火算法；精英约束

0 引言

火力分配作为对现代战争决策的重要环节，主要目的是将有限数量的武器，在复杂的战场环境下，通过合理分配给敌方威胁目标，获得最大程度的打击效果[1]。国内外已有很多文献对火力分配问题进行研究，研究的主要内容是在火力分配模型和求解算法两个方面[2-3]。

针对解决火力分配问题的方法，可分为传统的搜索算法和群智能优化算法[4]。传统的搜索算法寻优机制简单，一般处理规模较小的问题。伴随着群体智能优化算法的不断发展，传统算法的不足之处逐渐表现出来，群智能优化算法为问题优化求解提供了新的思路。而群智能优化算法的求解原理一般来源于自然法则和仿生学，相关的算法包括了遗传算法、生物地理学优化算法、粒子群优化算法等，或者是以上不同的优化算法进行混合使用[5-6]。针对来袭的多个无人机目标的火力分配，秦长江等人[7]使用改进的遗传算法对反无人机作战的火力分配进行优化。贺小亮等人[1]建立了基于模拟退火遗传算法的编队对地攻击火力分配模型。褚凯轩等人[8]提出基于蜂群算法的坦克阵地部署模型和坦克火力分配模型。

本文综合考虑威胁目标、武器的性能特点，结合协同作战需要建立起火力分配的数学模型，并提出一种改进的哈里斯鹰算法与模拟退火算法结合的混合算法（BEHHO-SA） ，通过仿真算例证明该模型的有效性，为解决坦克火力分配相关问题提供了准确、牢靠的理论支持。

1 算法优化

1.1 改进的哈里斯鹰算法（BEHHO）

双向经验引导与极端个体调控的哈里斯鹰算法（HHO Algorithm Based on Bidirectional ExperienceGuidance and Extreme Individual Regulation，BEHHO）是柴岩等人[9]在2022年提出的一种改进的哈里斯鹰优化算法，该算法作为一种元启发式优化算法，继承了哈里斯鹰算法[10] （Harris Hawks Optimization，HHO）的优化过程。BEHHO算法也通过求解过程的状态转移概率来证明其以概率1收敛至全局最优解。

BEHHO采用Circle混沌映射均匀化初始种群，相应计算采用公式（1） ：

其次，引入双向经验引导策略来强化算法的围捕机制，依托全局最优个体和历史最优个体的进化经验引导个体寻优方向，提升算法的收敛精度，相应的计算公式如下：

其中，Z （t）为当前个体的迭代位置、Z （t + 1）是下一次迭代时的个体位置，t 为迭代次数，Zr （t）是第t次迭代时，选取的随机个体位置，r1、r2、r3、r4、q 都是[0，1]范围内的随机数，Zb （t）为拥有最优适应度的野兔位置，Zm （t）为种群平均位置，up和down分别为搜索空间最大和最小边界值。

1.1.2 开采阶段

当|E|<1时，进入开发阶段，分为四种不同的搜索方式进行围捕：

（1） 软围捕策略

（2） 硬围捕策略

当|E|<0.5且η≥0.5时，采用公式（9） 进行计算。

（3） 快速俯冲软围捕策略

当|E|≥0.5且η<0.5时，如公式（10） 进行更新。

式中，V 是大小为1 × dim 的随机向量，dim 是问题的维度，LF 为莱维飞行的数学表达式。

（4） 快速俯冲硬包围策略

当|E|<0.5且η<0.5时，执行公式（13） 进行更新。

1.2 基于模拟退火的BEHHO 混合算法

模拟退火算法是一种随机寻优的方法，它从改进局部搜索算法出发，试图搜索优化问题的全局最优解[11]，李元香等人[12]对模拟退火算法早、中期的局部收斂特性进行了证明。

由公式（16）计算接受x'的概率P'，若Px'小于当前温度T 下产生的随机值rT∈[0，1]，则不更新当前解，否则更新。

其中，x 是某温度T'SA时的一个状态对应的解，x'为x 邻域内的随机解。

SA 算法的终止依据满足以下两点中的一点即可：1） 在相同温度下，经过K 次迭代最优解，而当前最优解不发生变化；2） 当前温度T'S 低于设定的最低温度Tmin，可以认为本次退火过程结束，退出循环。

1.2.1 精英约束策略

为了进一步提高算法收敛速度，引入一种精英约束策略。通过筛选高质量的候选解进入迭代过程的方式提高算法的收敛速度。

该策略受到精英策略的启发，当前种群中的精英个体对种群整体进化方向指导，提高算法的收敛速度[13]。在使用公式（4） 得到最优个体适应度之前，与预设适应度阈值τ 相比较，τ 值的设定应综合考虑实际应用运行时间、求解效果等因素。如果当前个体的适应度值f（X（t））>τ，则该个体视为精英个体，否则，为普通个体，使用公式（4） 进行变异。

1.2.2 BEHHO-SA 的基本步骤

把模拟退火机制引入BEHHO优化算法中，在每次BEHHO迭代结束时使用SA改进当前最佳解决方案，提高算法的收敛速度和精度。从而为求解火力分配模型提供有力支撑。改进后的BEHHO-SA算法实现伪代码如下：

2 火力分配建模

假设敌方有n 个威胁目标，我方有s 个作战单位，构建以下收益函数：

式中，s 表示我方作战单位的数量，n 表示敌方威胁目标的数量，uj 表示第j 个目标的威胁度，xij 表示某一时间段内第i 种己方作战单位打击第j 个敌方威胁目标的弹药数量（0表示不打击） ，qij 表示第i 个己方作战单位对第j 个敌方威胁目标的毁伤概率。

该火力分配数学模型的约束条件是公式（19） ：对某个目标的毁伤概率qj要高于毁伤概率门限qcj。

为避免火力资源相对充足、目标数相对较少情况下应用上述模型造成的火力资源浪费，还需考虑己方弹药消耗成本，要求最小化弹药成本：

其中，xij为第i种弹药对第j 威胁目标的数量，Vi为第i 种弹药的费用值，-Vi 表示归一处理后的第i 种弹药的单价费用，Vmin 表示最小的武器费用成本，Vmax 表示最大的武器费用成本。公式（20） 表示某次火力分配所投入的资源价值成本，即作战的成本越小越好。

建立了威胁度综合评价模型。首先根据不同类型敌方威胁目标建立了一个层次分析模型。目标威胁度分为三层：第一层是基础指标层，包括目标的类型、机动能力、打击能力、相对距离、相对速度、攻击角度等多个指标；将这些基础指标进行归一化处理后作为第二层的判断层，可分为静态威胁度指标、动态威胁指标中的环境指数指标；第三层是综合层，将第二层的三种指标作为3个维度进行加权计算，获得综合威胁度。

本文采用直接取整法对可行解空间进行处理，并对作战单位采用自然数的编码形式，将作战武器数量和敌方威胁数量相乘结果作为种群个体的长度，各个敌方威胁目标分配的相应作战单位视作种群个体，种群中个体可行解的各个分量是某类火力单元为各个目标分配的相应火力单元种类的数量，按顺序依次排列。

适应度函数用于判断每个个体在种群中的优劣程度。利用惩罚函数法[14]先把火力分配数学模型的公式（18） 、（19） 约束优化问题变成无约束的优化問题再利用，利用采用加权等效法将公式（18） 、（20） 优化模型转化为全局约束优化模型，然后再利用BEHHO-SA算法进行优化。

3 仿真验证与分析

设定火力分配案例，假设某次环境下，我方坦克阵营拥有3种作战武器（I1、I2、I3） ，设每种作战武器单价（V1，V2，V3） ，对不同Di距离（i=1，2，3，4） 的4个敌方威胁目标进行火力打击。其中要打击的敌方目标分别有D1距离的有生力量集群（W1） 、D2距离的碉堡（W2） 、D3距离的坦克（W3） 、D4距离的土木质发射点（W4） ，用威胁度综合评价模型设定来袭目标威胁度为[u1，u2，u3，u4]。

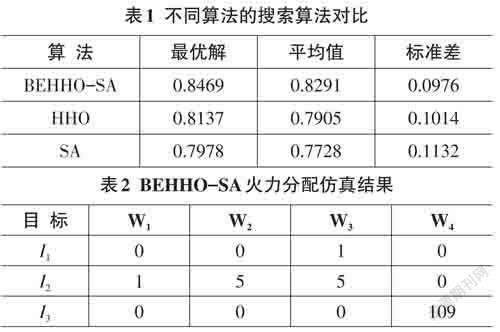
使用Python 应用程序编写进行模拟仿真，种群20，迭代次数为300，对该案例问题进行30次的多次重复计算，与标准SA算法、标准HHO算法进行对比，并将每一次的适应度函数计算结果记录下来。仿真后得到最优解如表1所示。BEHHO-SA算法优化得到的最终目标分配方案如表2所示。

4 结论

本文研究了基于BEHHO-SA算法的火力分配优化，相应约束条件给出了针对具体情境下的目标火力配置的数学模型，同时，通过在算法中增加精英约束策略，从而增加了目标种群多样性，提高了优化过程的效率，最后将其应用于目标分配问题建模中，通过多次重复试验，证明BEHHO-SA优化算法比HHO算法和SA算法的收敛精度更高，求解火力分配问题更稳定，提高解决全局目标最优组合配置问题的效率，为更多目标火力分配问题提供了理论依据。