偏心凸轮副时变乏油润滑数值分析*

2023-04-26高园杰李书义黄积松

润滑与密封 2023年4期

高园杰李书义郭峰黄积松

(青岛理工大学机械与汽车工程学院山东青岛 266500)

凸轮副是配气机构的核心零部件，摩擦副表面极容易产生磨损，进而影响配气机构工作精度和平稳性，降低内燃机的可靠性和使用寿命。因此，十分有必要对凸轮副摩擦润滑性能开展相关研究。王晓萌[1]结合工程中的实际载荷谱和速度工况参数，数值模拟了凸轮副在整个周期内的润滑油膜厚度、压力分布和摩擦因数等。王静和杨柿然[2]对充分供油下偏心轮机构时变弹流润滑问题进行了分析，阐述了偏心轮-挺杆在一个周期内的压力和膜厚分布情况。张建军等[3]分析了一个周期内8个典型瞬时偏心轮-挺杆副的压力、膜厚情况，讨论了不同椭圆比对润滑状态的影响。廖海平等[4]应用弹流润滑理论对凸轮基本尺寸进行设计，改善了凸轮与从动件间的润滑条件，减少凸轮的过度磨损。付振山等[5]利用数值计算方法，分析了凸轮在采用修正等速、修正梯形加速度和修正正弦加速度运动规律曲线时，整个分度周期内油膜厚度的变化。曹一等人[6]计算了从动件不同运动规律下凸轮机构的最小油膜厚度，发现凸轮基圆半径和转速对于最小油膜厚度有较大的影响。2016年，RAISIN等[7]以赛车中的凸轮从动件为例，研究了考虑剪切稀化下时变凸轮-挺杆系统的热弹流问题，分析了热效应、时变效应和流变效应对系统的影响。

润滑系统中，凸轮-挺杆副通常采用飞溅润滑，无法保证供油的稳定性和连续性，摩擦副时常在乏油润滑状态下工作。对乏油润滑的研究始于20世纪50年代末，DOWSON和HIGGINSON[8]首次提出了解决弹流问题的方案，并讨论了弹性变形和黏度对压力的依赖程度。HAMROCK[9]利用数值计算方法分析了供油膜厚与接触区油膜厚度的关系。1998年，WIJNANT[10]和CHEVALIER等[11]开发了新的乏油弹流润滑的模型，并对点接触弹流润滑中薄膜厚度的影响进行了数值研究。YIN等[12]以供油膜厚为输入参数，研究供油油膜厚度对弹流润滑的影响。LIU等[13]的研究表明，与充分供油对比，乏油条件下载荷、转速等工况参数对接触区润滑状态的影响更大。因此，有必要针对乏油条件下偏心凸轮副的润滑状态展开研究。

基于偏心凸轮-挺杆副，本文作者建立了时变乏油润滑模型，给出了一个周期内6个典型瞬时(60°、120°、180°、240°、300°、360°)的压力和油膜厚度的变化情况，并讨论了不同转速、不同黏度和不同初始载荷等参数对接触区润滑状态的影响。

1 控制方程

假设润滑油为牛顿流体，采用乏油条件下修正的Reynolds方程[14]：

(1)

式中：p为油膜压力(Pa)；h为膜厚(m)；ρ为润滑油密度(kg/m3)；η为润滑油黏度(Pa·s)；uR(t)为润滑表面沿x方向的卷吸速度(m/s)。

部分油膜比例因子θ定义为

(2)

式中：hf为实际润滑油膜的厚度(m)；h为两固体表面间的间隙(m)。

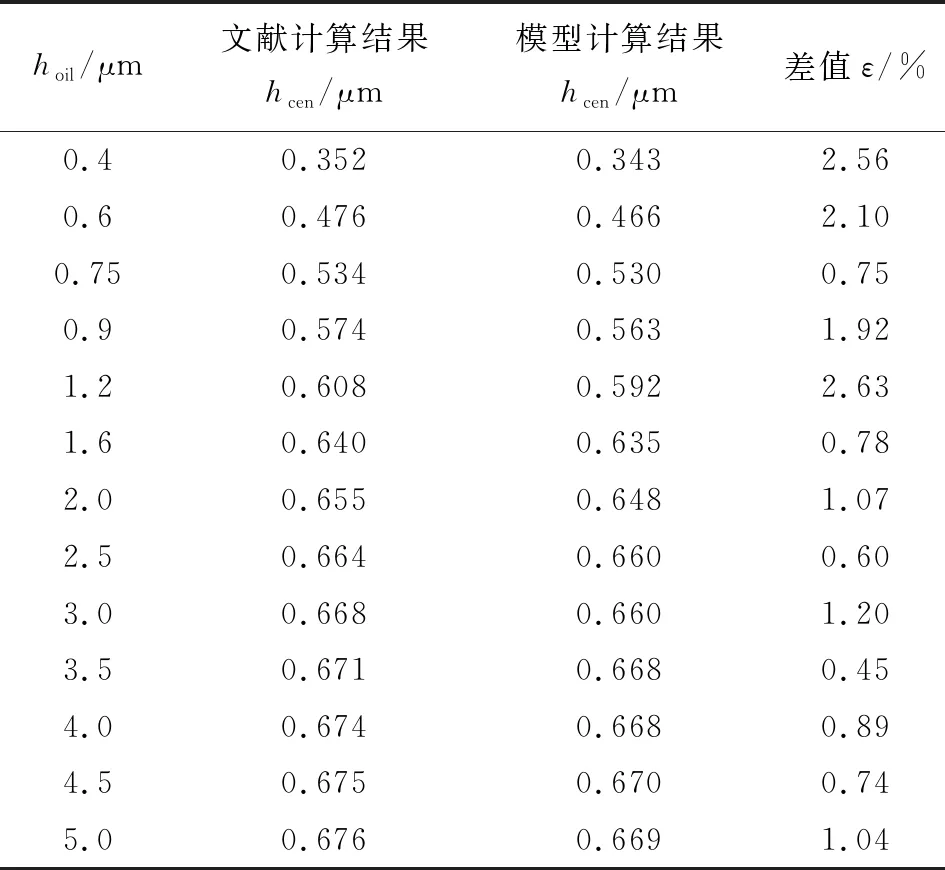
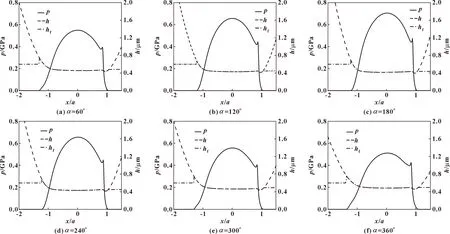
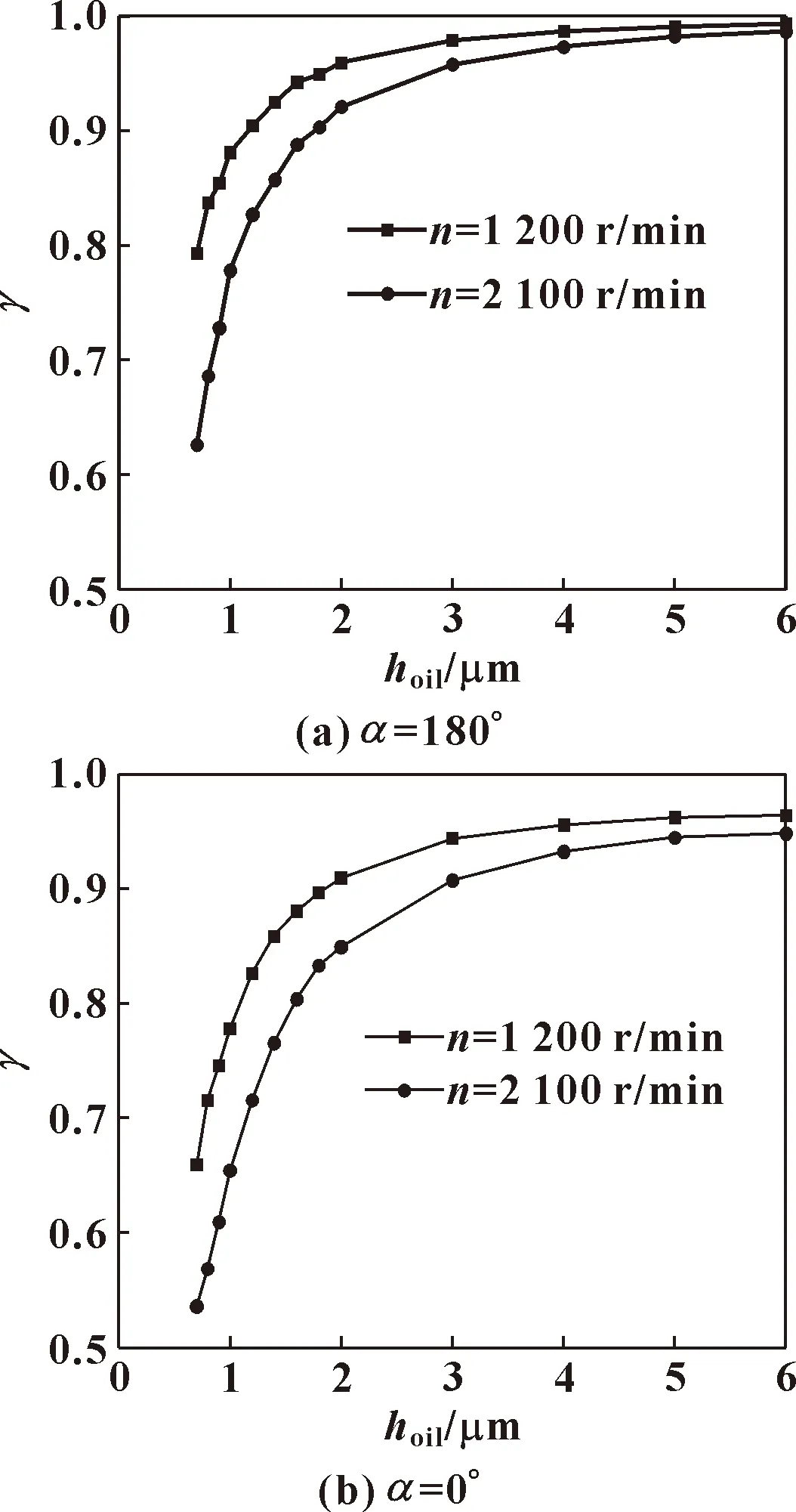
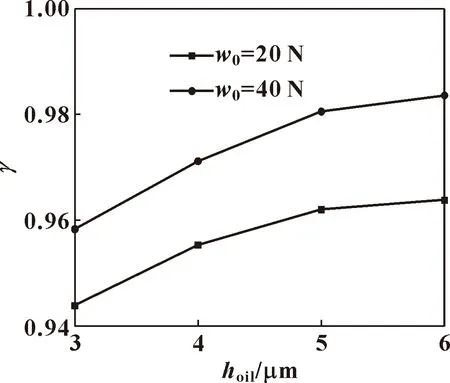
当处于乏油区的时候，润滑油无法充满两固体间隙，hf

方程(1)的补充求解条件为

p(x，y，t)[1-θ(x，y，t)]=0

p(x，y，t)≥0，0<θ(x，y，t)≤1

(3)

为了使方程的解统一，2个独立变量θ和p应满足：

p(x，y，t)>0时，θ(x，y，t)=1

p(x，y，t)=0时，0<θ(x，y，t)<1

(4)

方程(1)的边界条件为

p(xin，y，t)=p(xout，y，t)=p(x，yin，t)=p(x，yout，t)=0

(5)

式中：xin、xout、yin、yout为计算域的边界坐标(m)。

总间隙方程：

(6)

式中：h00为刚体中心膜厚(m)；Rx和Ry分别为两固体在x和y方向的综合曲率半径 (m)；E′为综合弹性模量(Pa)。

Roelands黏压关系：

η=η0exp{A1[-1+(1+A2p)α/(A1A2)]}

(7)

式中：η0为润滑油的环境黏度(Pa·s)；A1=lnη0+9.67，A2=5.1×10-9Pa-1；α为Barus黏压系数(Pa-1)。

Dowson-Higginson密压关系：

(8)

式中：ρ0为润滑油的环境密度(kg/m3)；A3=0.6×10-9Pa-1；A4=1.7×10-9Pa-1。

载荷方程：

∬p(x，y，t)dxdy=wR(t)

(9)

其中：载荷wR(t)随凸轮旋转角度变化，如图1(a)所示，其表达式为

(10)

式中：w0为初始载荷(N)；以NUT代替时间t(s)，将凸轮一个旋转周期划分为NT2(NT2=360)个瞬时，NUT的取值为1～NT2。

此外，数值计算过程中凸轮转速n为恒定值，接触区卷吸速度随时间变化，如图1(b)所示，其表达方程[15]为

图1 一个旋转周期内载荷和卷吸速度变化规律(n =1 200 r/min，e=4 mm，r=20 mm)

(11)

式中：n为转速(r/min)；r为基圆半径(mm)；e为偏心距(mm)。

文中设定偏心凸轮基圆圆心离表面最近时转角为0°，则距离表面最远时转角为180°。如图1所示，当凸轮转角为0°时，载荷最小，卷吸速度最大；而凸轮转角为180°时，载荷最大，卷吸速度最小。

2 数值方法

文中凸轮副弹流润滑模型的求解采用多重网格技术[16]，其中多重网格法用来求解压力场，而多重网格积分法则用来求解由压力而产生的表面弹性变形。采用5层网格，最高层网格节点数为512×512，取x、y方向边界计算域为

{(x，y)|-4.5≤x/a≤2.5，-4.5≤y/a≤4.5}

3 算例与结果

文中将凸轮一个旋转周期划分为360个瞬时(NT2=360)，NUT的取值为1～NT2 ，即凸轮每旋转1°计算一次接触区的压力和膜厚，时间间隔Δt=60/(n×NT2)。因为偏心轮-挺杆副是作周期性运动，求解时就不得不考虑周期性问题。每个瞬时，都是采用前一个瞬时计算得到的压力终值作为迭代初值，进行压力和膜厚的计算，整体计算流程如图2所示。润滑模型基本输入参数如下：综合弹性模量E′=2.26×1011Pa，黏压系数α=2.2×10-8Pa-1，综合曲率半径Rx=0.02 m，为防止假收敛，最少循环计算次数Large=5。

图2 计算流程

在最稠密网格层上，采用压力和载荷的相对误差为收敛判据：

(12)

(13)

由于凸轮周期性旋转特性，为保证结果稳定性增加周期误差收敛判据：

(14)

式中：上标“new”和“old”表示一次松弛迭代前后压力；上标“now”和“pre”为前后2个凸轮旋转周期内同一瞬时压力。

为了验证程序的正确性，文中计算了不同供油膜厚下的中心油膜厚度hcen，并与YIN等[12]的计算结果做对比，如表1所示，发现计算结果最大偏差为2.63%，因此可以验证计算模型的正确性。

表1 模型验证

3.1 不同凸轮转角下的润滑状态

图3给出了凸轮旋转一周中6个典型瞬时y/a=0截面的压力和膜厚分布曲线，其中有效供油膜厚hoil=0.6 μm、转速n=2 100 r/min、初始载荷w0=20 N、润滑油黏度η0=0.08 Pa·s。

从图3中可以看出，随着凸轮转角的增大，压力逐渐增大，油膜厚度逐渐减小；当凸轮转角为180°时，最大压力达到0.70 GPa，最小膜厚为0.42 μm，如图3(c)所示；随后压力逐渐减小，膜厚逐渐增大，当凸轮转角为360°的时候，压力达到最小值0.51 GPa，膜厚达到最大值0.48 μm，如图3(f)所示。此外，由于供油量不足(hoil=0.6 μm)，在入口区润滑油无法填满两接触表面形成的收敛空间，形成乏油区，而随着两固体间隙减小，使得在近接触区处才能将两固体间隙完全充满。在凸轮转角为360°(即0°)时，油膜形成的坐标x/a=-1.36；而凸轮转角为180°时，油膜形成的坐标x/a=-1.21，形成完整油膜的位置更靠近接触区中心，乏油也更为严重。这是因为当凸轮转至180°时，对应的工况卷吸速度最小、载荷最大，最终导致该转角下的中心膜厚最小。因此，相同供油量下凸轮转角不同，接触副呈现不同的润滑状态，凸轮转角为180°时，乏油情况最严重。

图3 不同凸轮转角下接触区y/a=0截面压力和膜厚分布

凸轮副接触区润滑状态受供油量和凸轮转角的影响较大，有必要对其影响规律进行深入分析。由于偏心轮几何结构的对称性，选取0°、90°、180° 3个凸轮旋转角度来研究。文中用不同凸轮旋转角度下的中心油膜厚度hcen与充分供油下中心油膜厚度hcen-fully的相对中心膜厚，即γ来评估接触区的乏油程度，定义式为

γ=hcen/hcen-fully

(15)

如图4所示，考察不同凸轮旋转角度下，相对中心膜厚γ随供油膜厚hoil的变化规律，其中w0=20 N，n=1 200 r/min，η0=0.08 Pa·s。总体来看，3个旋转角度下相对中心膜厚曲线变化趋势大体相同，相对中心膜厚γ随着供油膜厚的逐渐减小，先是缓慢降低，该阶段供油膜厚改变对接触区润滑状态影响并不十分明显；但当供油膜厚hoil约小于2 μm时，相对中心膜厚γ开始急剧下降，中心膜厚对供油膜厚的改变非常敏感，乏油边界已接近接触区入口处，处于较为严重的乏油状态。在具体数值上也有差异，凸轮转角为0°时相对中心膜厚变化速度最快，乏油程度改变迅速，而180°时相对中心膜厚变化较慢，乏油程度相对较低，90°则处于两者之间。这是因为凸轮转角为0°时，接触区卷吸速度最大而压力最小，接触区润滑油膜对供油膜厚更为敏感，故该角度下相对中心膜厚相对变化较大，而180°时情况却恰好相反。

图4 当凸轮转角为0°、90°和180°时，相对中心膜厚γ随供油膜厚的变化(w0=20 N，n=1 200 r/min，η0=0.08 Pa·s)

即使如此，在旋转角度为180°时，如图5所示，在高载荷、低转速的工况下，中心油膜厚度的值仍是最小的。因此，凸轮接触副润滑状态与供油膜厚直接相关，且会受到凸轮旋转转角的影响，凸轮在运转过程中，最危险工况为α=180°时，但同时也要警惕α=0°时的油膜厚度，因为该工况下乏油速度最快。

3.2 不同工况对润滑状态的影响

为了对润滑状态进行进一步的研究，文中继续探讨不同工况对相对中心膜厚γ随供油膜厚hoil变化的影响。

图6给出了不同转速和凸轮转角下相对中心膜厚γ随供油膜厚的变化曲线，其中润滑油黏度η0=0.08 Pa·s，初始载荷w0=20 N，转速为1 200和2 100 r/min。可以看出，2个凸轮转角(0°/180°)下凸轮旋转速度并没有改变相对中心膜厚随供油膜厚减小而降低的趋势，且高凸轮转速工况相对中心膜厚γ始终小于低速工况，转速越高使得相对中心膜厚变化越快，即相同供油膜厚下凸轮转速较高的工况其乏油情况越严重。而且，比较图6(a)、(b)可知，当凸轮旋转角度α=0°，对应的卷吸速度最大时，乏油整体更严重。因为凸轮转速越高意味着接触区需要更大量的润滑油供应以达到充分润滑状态，限量供油下的工况使得润滑油供应得不到满足，速度越高反而使得接触区乏油状态越严重。由此，当凸轮转速大时，虽然油膜厚度更大，但是乏油速度也更快，乏油程度更深，高转速对接触区的润滑状态影响较大。

图6 不同转速和凸轮转角下，相对中心膜厚γ随供油膜厚的变化(η0=0.08 Pa·s，w0=20 N)

文中继续探讨黏度对润滑状态的影响。选取初始载荷w0=20 N，转速n=1 200 r/min，黏度为0.08和0.2 Pa·s，分析2个凸轮旋转角度(0°/180°)下相对中心膜厚γ随供油膜厚的变化规律。可以看出，润滑油黏度的改变并不会影响相对中心膜厚γ随供油膜厚减小而降低的趋势，且黏度的增加会使得相对中心膜厚变化更为剧烈。充分供油条件下，润滑油黏度越大接触区润滑油膜厚度越高，但限量供油下由于润滑油供应量不能满足接触区所需，进而使得接触区油膜厚度降低，造成相对中心膜厚进一步降低，即相同供油条件下，润滑油黏度越高使得接触区表现出乏油越严重的情况。而且，比较图7(a)、(b)可知，当凸轮旋转角度α=0°时，乏油整体更严重。由图1(b)已知，偏心轮在0°时卷吸速度最大，卷吸速度的增加使接触区中心膜厚hcen和充分供油状态下的中心膜厚hcen-fully均增大，但是在限量供油条件下，高卷吸速度使接触区中心油膜厚度加速衰减，且黏度越大衰减的速度越快，乏油更严重。因此，润滑油黏度大的工况乏油速度更快，乏油程度更深，且卷吸速度增大会使得乏油程度加深。

图7 不同黏度和凸轮转角下，相对中心膜厚γ随供油膜厚的变化(w0=20 N，n=1 200 r/min)

为了进一步探讨不同工况对接触区润滑状态的影响。文中选取转速n=1 200 r/min，润滑油黏度η0=0.08 Pa·s，对接触区载荷进行了研究。图8给出了不同初始载荷20和40 N (初始状态的最大赫兹接触应力为0.50和0.62 GPa)下相对中心膜厚γ随供油膜厚的变化规律。可以看出，在相同的凸轮转角下，不同的初始载荷下膜厚的下降趋势非常相似，两条曲线的差值非常小，这与Hamrock-Dawson中心膜厚公式相呼应，即载荷对中心膜厚的影响非常小。文中将图8(b)放大，如图9所示，发现凸轮转角为0°时两条曲线存在差值，且供油越充分差距越明显。由于α=0°时接触区卷吸速度较大，中心膜厚相对更大些，接触区润滑状态能够体现出载荷的影响，这与以上转速和黏度的分析结果一致；而在α=180°时卷吸速度低且载荷最大，接触区膜厚相对较低，载荷改变不易引起油膜厚度的变化。因此，可以得出，载荷对接触区的润滑状态的影响较小，仅凸轮转角为0°时卷吸速度最大，接触区润滑状态能够体现出载荷影响。