微型无油空气压缩机活塞环热力耦合分析及其结构优化

常建国

(西安工业大学 机电工程学院,西安 710021)

0 引言

微型无油空气压缩机具有体积小、质量轻、排出空气清洁等优点,广泛用于医疗、食品、冷却、气动弹射和潜水呼吸等领域[1]。活塞环是空气压缩机的重要零件之一,微型无油润滑空气压缩机活塞环通常由聚四氟乙烯制成,在高温、高压、无油润滑工况下不易保证聚四氟乙烯活塞环的可靠性[2-3]。

文献资料中关于活塞环分析研究工作的报道较多。叶建春等[4]基于有限元法对无油润滑压缩机的活塞环强度进行了分析评估。孙秀永[5]对活塞环的热传导进行了分析,得到了活塞环的温度分布特点,并在热机耦合下对活塞环强度进行了分析。丁瑞[6]利用ANSYS软件对无油润滑空气压缩机活塞环进行了热力耦合分析,得出了活塞环的应力、应变的分布情况,并利用ANSYS二次开发工具对耦合场下活塞环进行了仿真分析,探究活塞环结构参数对活塞环应力、应变的影响。在活塞环优化方面,李炯[7]利用遗传算法对BP神经网络进行改进,并对活塞环结构参数进行了优化。研究表明,结构参数优化后活塞环与缸套之间的摩擦损失功率比优化前降低了14.54%。卢鹏[8]对活塞环进行了结构设计,利用正交实验对活塞环的摩擦损失和窜气量进行计算分析后得出活塞环最优结构设计参数。丁加岑[9]研究了活塞环开口的结构参数对活塞组窜气及机油消耗的影响,并对活塞环开口进行结构优化,取得了较好的效果。汤义虎等[10]基于反演法,研究了活塞环廓形对摩擦因数和摩擦力的影响,并对活塞环进行了结构优化。结果表明,优化后活塞环廓形产生的摩擦力和摩擦因数更小。

虽然研究和技术人员采用不同的方法对空气压缩机活塞环做了很多研究分析工作,但是文献资料中鲜有响应面法用于活塞环的报道。响应面法是寻求最优参数的方法,本文根据热力耦合分析得到无油空气压缩机聚四氟乙烯活塞环应力及形变的分布结果,基于响应面法对活塞环结构进行优化设计,以期在实际工程应用中为活塞环结构优化设计提供参考。

1 活塞环模型及边界条件

1.1 活塞环模型

以某微型无油空气压缩机聚四氟乙烯活塞环为研究对象。该空气压缩机与活塞环参数示于表1。活塞环采用开口活塞环,开口方式为斜口,开口角度为50°,有助于提高活塞环的密封性能[11]。利用SOLIDWORKS软件建立活塞环三维模型如图1所示。

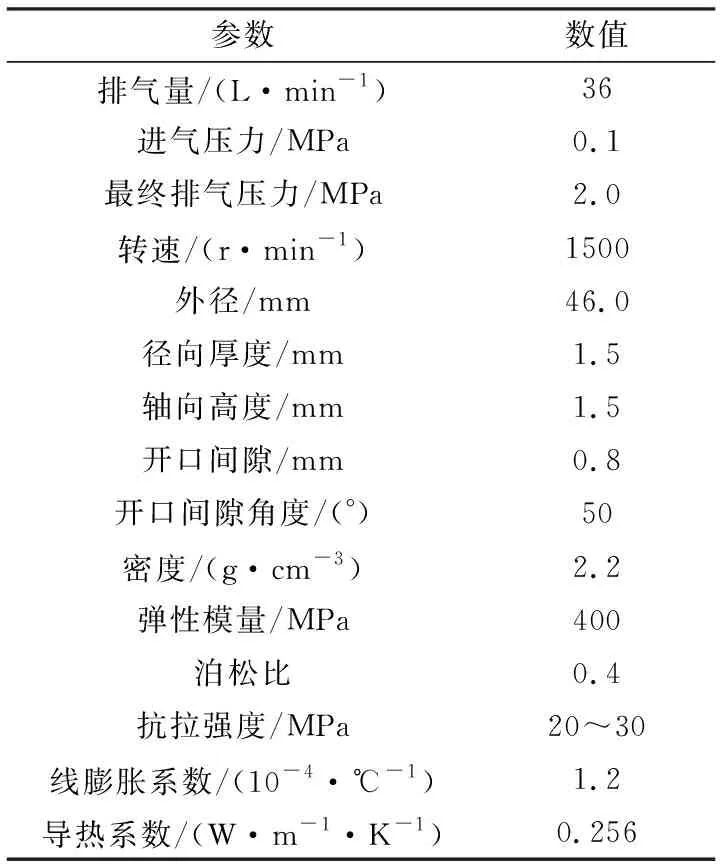
表1 微型无油空气压缩机及活塞环参数

图1 活塞环三维模型

微型无油空气压缩机工作时气缸内温度最高可达200 ℃。聚四氟乙烯活塞环耐高温性能和强度弱于金属活塞环,需考虑工作温度与机械载荷共同作用下聚四氟乙烯活塞环应力及变形分布情况。为此,利用ANSYS Workbench对所建模型进行六面体单元网格划分,共形成网格单元19 572个,节点97 547个,如图2所示。

图2 活塞环网格模型

1.2 温度场计算

活塞环温度场计算采用如下传热方程

(1)

(2)

式中:α为对流换热系数;Tf为活塞环周围的介质温度。

对应的泛函方程为

(3)

式中:λ为导热系数;S为活塞环表面边界。

根据式(3)活塞环单元的泛函方程为

(4)

则活塞环模型的泛函方程为

(5)

泛函极值条件为

(6)

式中:Je为活塞环边界与其划分单元的重合区域;N为活塞环网格划分之后的节点数量。

1.3 边界条件

1.3.1 热边界条件

根据表1中空气压缩机的相关参数,采用经验公式计算可得活塞环上表面换热系数为345 W/m2·℃,活塞环下表面换热系数为210 W/m2·℃。活塞环内表面换热量非常少,故作绝热过程处理[12]。根据相近型号活塞式空气压缩机的相关实验数据[13-15]及参考文献[6],活塞环上表面介质温度确定为106.0 ℃,内表面介质温度为102.0 ℃,下表面介质温度为90.0 ℃。由于活塞环外表面与气缸壁摩擦生热,外表面温度相对较高。根据文献[16]的数据,聚四氟乙烯活塞环内外表面温差达17.5 ℃,且外表面温度约为112.5 ℃。

1.3.2 边界约束条件

活塞环边界条件主要包括气体压力、活塞环本身具有的初弹力、惯性力以及活塞环外侧与气缸壁之间的摩擦力[17]。活塞环具体受力分析如图3所示。

图3 活塞环受力分析

微型空气压缩机运行过程中,活塞环的工况十分复杂,在有限元仿真分析过程中需要对其载荷进行适当简化[6],简化条件为

(1)活塞环因热膨胀与气缸套内壁之间产生的摩擦力与气体压力相比而言非常小,不予考虑。

(2)聚四氟乙烯活塞环本身的初弹力与气体压力相比非常小,对活塞环的影响可以忽略不计,不予考虑。

(3)聚四氟乙烯活塞环本身质量较轻,在工作过程中产生惯性力很小,不予考虑。

1.4 活塞环机械载荷的分布情况

该微型空气压缩机工作时活塞顶部向下第一道活塞环承载最大,故将该活塞环作为计算分析对象。活塞环的不同位置,受到的气体压力大小也不同,其分布情况如图4所示(图中Pg为气体压力)。

图4 活塞环气体压力分布示意图

活塞环三维模型边界条件如图5所示。图中边界1为活塞环下端面与活塞环槽相接触区域,受活塞的轴向(z方向)约束,位移为零。边界2为活塞环外侧面,受气缸套约束,径向位移为零。边界3是活塞环内侧面,其承受气体压力P1大小为1.58 MPa,为均布载荷。边界4是活塞环自由端面即上端面,承受气体压力为2.10 MPa。

图5 活塞环边界条件

2 活塞环有限元分析

2.1 温度场分析结果

图6所示为活塞环整体(图(a))和截面(图(b))的温度场分布云图。

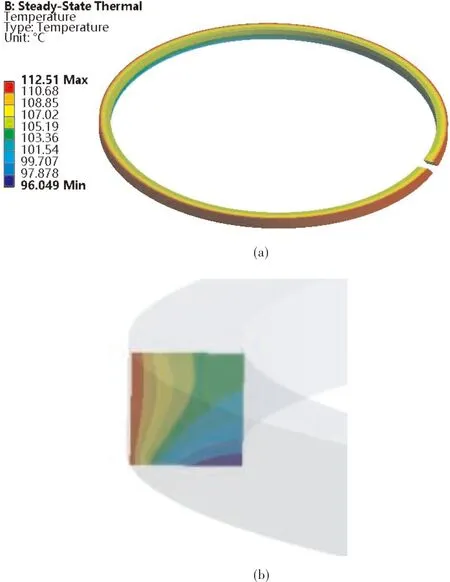
图6 活塞环的温度场分布云图:(a)整体;(b)截面

由图6(a)可以看出,活塞环温度整体分布从外表面到内表面逐渐降低,且活塞环的下表面区域温度最低,约为96.05 ℃,略高于区域介质温度,这主要与下表面的气流热交换有关。此外,计算结果表明,最高温度约为112.51 ℃,位置在活塞环的外表面,这与气缸内壁间的摩擦作用有关。截面温度场分布云图(图6(b))同样表明,活塞环由外表面到内表面温度逐渐降低。

2.2 热力耦合分析结果

活塞环热力耦合分析的边界条件包括载荷、温度及位移约束条件,将前述温度场仿真分析结果导入静力学分析中,可得到活塞热力耦合分析结果。

图7所示为计算所得活塞环应力分布云图。由图7(a)可见,活塞与活塞环接触的边缘区域应力集中明显。由图7(b)可见,应力集中区域沿径向由外向内应力逐渐减小,这与活塞环实际工作受力情况相符。应力最大点在活塞环开口左端下表面,应力值为21.08 MPa,这由上表面气体压力作用所致。

1) The basic principle of the UltraLab network experiment platform

图7 活塞环应力分布云图:(a)整体;(b)应力集中区域放大图

热力耦合作用下活塞环的变形量不均匀且开口区域较大(图8(a))。此外,根据图8应变云图可得:x方向最大变形量为0.28 mm,位置为活塞环四分之一处;y方向最大变形量为0.48 mm,位置在活塞环开口处,一侧向内收缩一侧向外膨胀,且从开口处到环背脊逐渐减小。

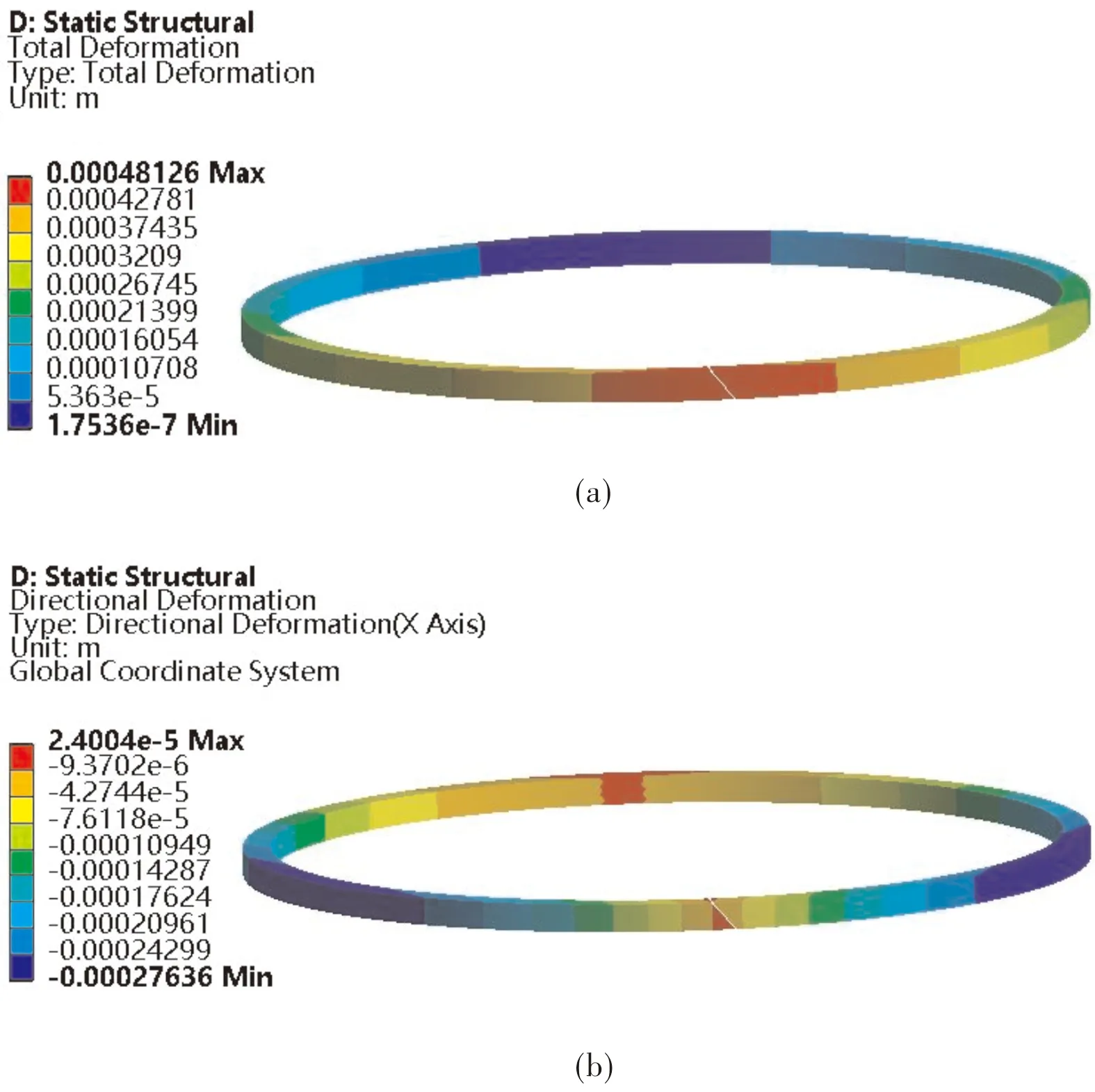
图8 活塞环应变分布云图:(a)整体;(b)x方向;(c)y方向

3 活塞环优化设计

活塞环优化设计采用响应面法,该方法能很好地解决设计参数与优化目标之间难以建立显示函数的问题,是一种建立目标函数与约束函数近似模型的方法。响应面法通过对指定设计空间选取大量设计点进行试验设计,根据设计点计算结果拟合出设计变量与优化目标之间的响应面,再利用所得响应面进行优化求解[18]。据此,活塞环结构参数优化流程包括活塞环的参数化建模、指定设计变量、确定目标函数与约束条件、灵敏度分析、DOE试验设计、响应面拟合、结果优化分析,如图9所示。

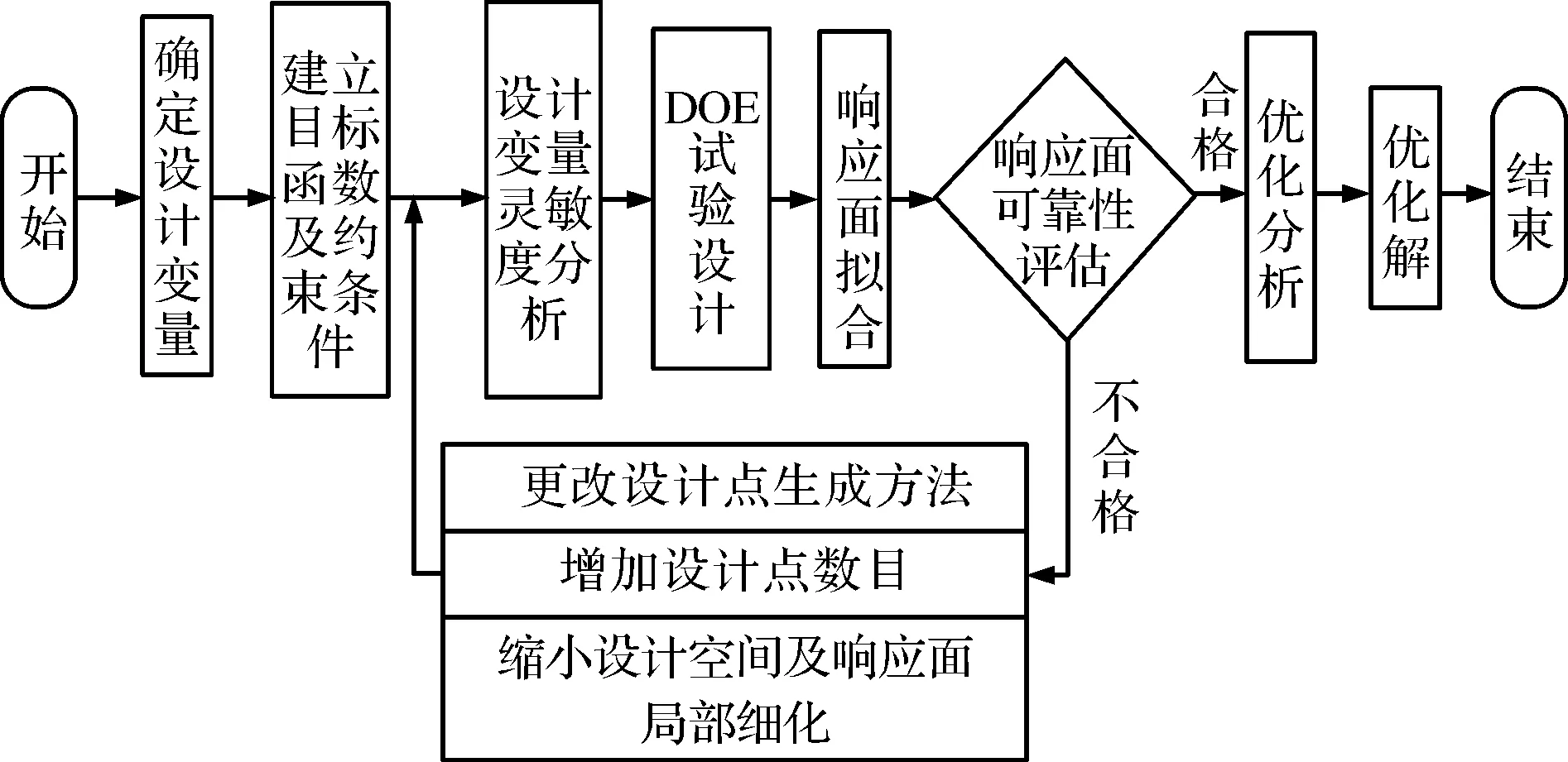
图9 活塞环结构参数优化流程

3.1 设计变量

活塞环设计参数包括开口间隙δ、开口间隙角度β、轴向高度h、塞环内径D以及径向厚度t。此外,考虑实际工作过程中活塞环与活塞的接触方式,将活塞与气缸之间的半径间隙L也作为设计参数之一。根据实际使用工况,微型空气压缩机活塞环设计参数的取值范围示于表2。

表2 微型无油空气压缩机及材料参数

3.2 优化目标及约束条件

机械结构设计的目的是设计出安全可靠的结构。对于非金属活塞环而言,其强度远小于金属活塞环。因活塞环的应力和形变均为L、δ、β、h、D和t的函数,因此可将应力函数σ=g(L,δ,β,h,D,t)和应变ε=φ(L,δ,β,h,D,t)作为优化函数,将活塞环的最大应力、最大应变作为优化目标,并将材料抗拉强度(σb≤20 MPa)作为约束条件。则建立活塞环的优化数学模型为

fσ(L,δ,β,h,D,t)=max(g(L,δ,β,h,D,t))

(7a)

fε(L,δ,β,h,D,t)=max(φ(L,δ,β,h,D,t))

(7b)

式(7a)和(7b)中的各变量应满足表2中的取值范围。

3.3 敏感度分析

敏感度反映了设计变量对优化目标的重要程度。对活塞环进行结构参数优化前,首先对其进行敏感度分析,结果如图10所示。

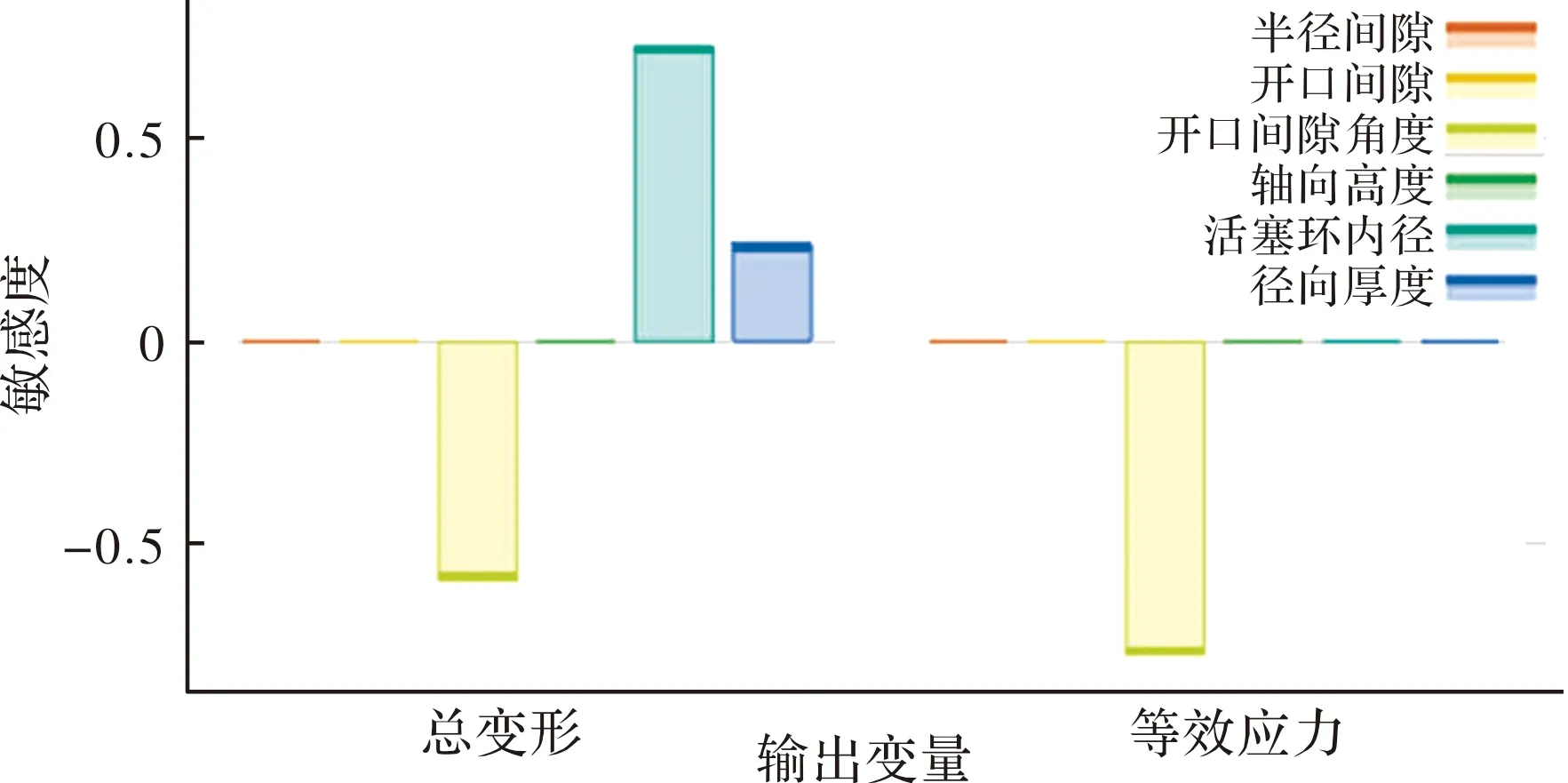
图10 设计变量敏感度分析

3.4 DOE试验设计

DOE试验设计直接影响响应面的精度,因此,选取合适的方法进行DOE试验设计至关重要[19]。DOE试验设计有多种方法,其中OSF方法能够在设计空间中均匀生成样本点,样本覆盖比较全面,为此,本文采用OSF法进行DOE试验设计,生成的样本点如图11所示。

3.5 响应面拟合函数及响应面评估

选用Workbench中Kriging类型响应面法建立响应面,该方法是一种多维插值技术,能够更好地处理非线性较强的复杂工程问题,且具有更强的预测能力[20]。采用该方法建立的应力及应变响应面如图12所示。由图12(a)可知,随着开口间隙角度的增大以及内径的减小,活塞环应变值逐渐减小。由图12(b)可知内径对于应力值的影响较小,而开口间隙角度越大应力值越小。

图12 Kriging响应面拟合:(a)应变;(b)应力

为保证响应面的准确性还需要对响应面进行评估,因此需要添加验证点来验证响应面模型的准确性。添加验证点并通过对响应面多细化之后,Kriging响应面的拟合优度散点图如图13所示。根据图13可知最大位移、最大等效应力两个输出参数的拟合情况,据此可以判断响应面模型的拟合优度。由图13可见,最大位移与最大等效应力的预测值与数值试验值均分布在图对角线附近,表明Kriging响应面的拟合度良好,响应面比较可靠。

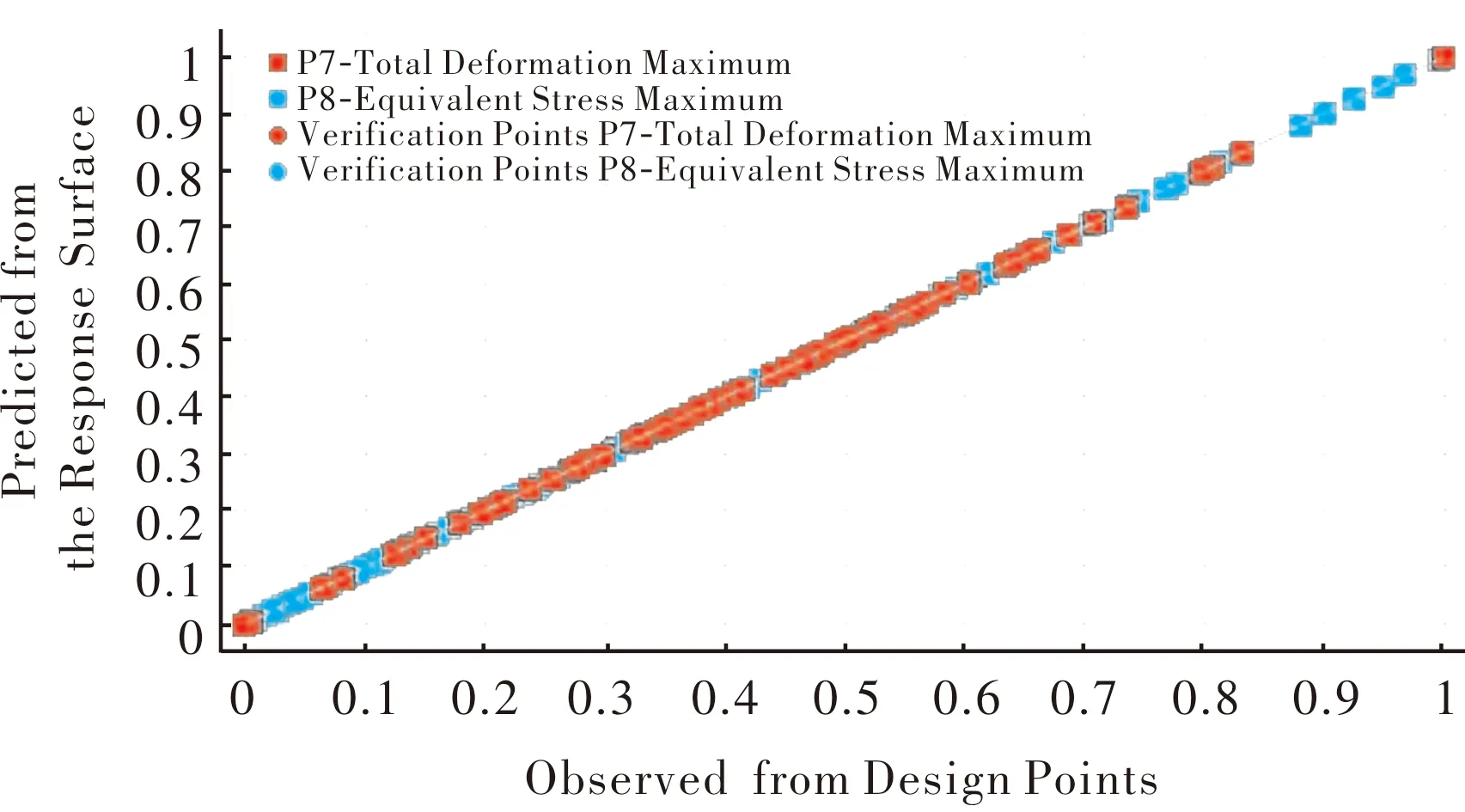
图13 Kriging响应面的拟合优度散点图

4 活塞环结构优化

响应面建立后,能够获取响应面中的近似响应点,然后利用响应面搜索全局的最优设计方法——多目标遗传算法(MOGA)[21]——进行优化。根据设计变量与优化目标的数量,确定初始样本数量为100,每次迭代样本数量为100。为了避免过早收敛导致优化结果不理想,将最大允许的pareto设置为70%,收敛稳定性设置为2%,最大允许迭代次数为20次。通过优化求解得到3组候选点及其验证点如图14所示。

图14 优化后三组候选点

通过比较,选取第一组候选点作为最优设计点,该设计点与其验证点对比误差小于5%。优化后应力云图分布如图15所示,优化后最大应力值约为17.3 MPa,与初始设计点对比应力值下降了约17.8%。

图15 优化后应力云图

优化后应变云图分布如图16所示,最大位移约为0.46 mm,位移值下降了约4.6%。

图16 优化后应变云图

5 结论

根据活塞环的实际工况对活塞环进行了热力耦合分析,确定了活塞环工作时的最大应力与最大位移。利用SOLIDWORKS与ANSYS Workbench建立了活塞环有限元参数化建模,将DOE试验设计、灵敏度分析、构建kriging响应面、多目标响应面优化相结合对活塞环的应力与位移进行了优化。使活塞环的最大应力值由原来的21.0 MPa减小到17.3 MPa,降低约17.8%,最大变形从0.48 mm减小到0.46 mm,降低了约4.6%,可为活塞环的优化设计提供参考。