基于谐响应分析的调节器壳体动态特性研究与改进

冯 涛,杨军杰,赵 彬,贾 佳

(中国航发西安动力控制科技有限公司,西安 710077)

0 引言

正弦振动是随时间按正弦(或余弦)函数变化的振动,常出现在存在旋转、脉动、振荡现象的电子产品和舰船、飞行器、各类车辆等装置上[1]。航空燃油调节器做为飞机发动机附件设备因受到飞机发动机高速旋转振动载荷变化产生周期振动激励,对其结构会产生直接影响,严重的会造成机体振动断裂破坏。采用谐响应分析方法可以用来研判共振的发生,提前采取措施,减小共振以及其他受迫振动引起的有害现象,从而保证设备的安全稳定[2],因此正弦振动试验是考察航空产品结构可靠性设计和环境适应性要求的主要内容之一。

现有某型航空燃油泵调节器,其作为航空发动机燃油附件安装在发动机附近承受发动机振动带来的正弦载荷,其壳体在正弦振动试验阶段出现壳体开裂,为了适应机载环境的性能与结构可靠性要求,需要对问题产品改进设计。本文通过仿真手段,建立试验件的振动试验仿真模型,分析产品在正弦振动载荷条件下的振动响应,并通过实际试验与仿真结果进行对比,验证仿真分析的可行性,对比改进结构与原结构的动态特性,分析产品振动性能薄弱环节,检验产品振动安全裕量,并进行了多次减振优化仿真分析,为产品结构动力学设计提供参考,所做工作帮助提高了产品抗振性能。

1 正弦振动的数学描述

航空燃油泵调节器受发动机旋转振动载荷产生周期振动激励。

振动系统可看成由质量、弹簧和阻尼器组成,一般认为弹簧与阻尼器皆为线性元件,即弹性力与位移成正比,阻尼力与速度成正比,具有比例阻尼的多自由度系统其运动方程为[3]:

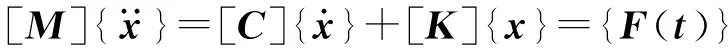
(1)

其中:[C]=α[M]+β[K],α和β为比例常数; [C]为阻尼矩阵,复合式的阻尼称为比例阻尼;[M]和[K]分别为质量矩阵和刚度矩阵;F(t)表示激振力。

一般情况下旋转机械受到的动载皆为周期性激扰,可视为简谐力,当激振力为简谐力时,即F(t)=f(t)sin(ωt),加入简谐载荷下受迫振动的运动微分方程为:

(2)

移响应方程为:

{x}={A}sin(ωt+φ0)

(3)

其中:φ0为位移响应滞后激振力的相位角;{A}为位移幅值向量。

将式(3)代入式(2)得:

谐响应分析用于确定结构在承受随时间按正弦变化的载荷时的稳态响应,在一定频率ω范围及间隔下,通过有限元软件对上述方程的求解,能够计算出相应振动位移,从而得出振幅-频率关系,进而根据曲线得出峰/谷值频率。通过振动谐响应分析,还可得出应力、应变及加速度与激振频率之间的响应曲线,能够帮助预测结构的持续动力特性,从而验证其设计是否能够克服疲劳、共振及其他受迫振动引起的有害结果[4]。

2 调节器谐响应分析

本文以某型航空燃油泵调节器壳体为例,在前期振动试验基础上,通过对整机有限元仿真模型的标定调试,根据仿真结果,对其壳体结构在工作状态下的振动进行了分析、标定与优化。

在我国跨境电商物流的发展过程中，基础设施的不完善及体系不完整等，物流的成本较高，根据相关资料得出结论，从成本来看，我国跨境电商物流的成本远远高于其他国家甚至是国际标准。跨境电商物流需要考虑的问题多而复杂，涉及国内物流、国内海关、 国际运输、 国外海关、 国外物流众多环节，在实际操作中风险很大，因此，在一定程度上大大增加了我国跨境电商的物流成本。

2.1 振动分析模型建立

根据该调节器几何结构,建立调节器组件装配模型如图1所示。调节器壳体组件在进行振动实验时,依靠12个螺钉将壳体组件固定在振动实验台工装上。

图1 调节器组件装配模型

根据振动试验中组件的实际安装情况,设置工装底板螺栓孔区域为固定约束。分析时,振动载荷通过工装底板约束施加,振动载荷X、Y、Z三个方向分别按最大20g施加。

2.2 阻尼比的选取

在进行谐响应分析中,振动系统的阻尼比的确定是关键问题,工程中阻尼比经常是取经验值,容易造成分析结果跟实际不符。阻尼对模态频率的影响很小,其主要作用是降低共振处的振幅,阻尼越小,共振的振幅会越大,阻尼比的确定也影响着对系统分析结果的评定。

目前阻尼问题研究的还不是很透彻,并没有很多的理论支持,本文结合试验测试的数据,采用半功率法估算出调节器组件结构的阻尼比,并以此进行谐响应分析。

半功率带宽法是根据简谐振动系统共振时的振幅放大因子曲线来推算阻尼比,特别是在环境激励的情况下,被广泛用于测量结构阻尼比。其计算公式如下[5]:

a、b两点称为半功率点,这两点所对应的频率为:

或(fa/fn)2=1-2ξ,(fb/fn)2=1+2ξ

由此可得:

由于在小阻尼情况下fa≈fn≈fb,所以,

其中:ξ为阻尼比;fn为系统共振频率;H是共振峰幅值,fa、fb是幅值为0.707H时所对应的两个频率点[6-7]。

图2 振系的幅频特性及半功率点

通过上述公式和试验实测峰值数据,计算出调节器组件装配模型的阻尼比为:

将该阻尼比应用到调节器装配组件三个方向的谐响应分析,得到原壳体传感器位置处的仿真频响曲线与试验曲线。X方向振动和试验频响曲线对比如图3所示,Y方向振动和试验频响曲线对比如图4所示,Z方向振动和试验频响曲线对比如图5所示。

图3 X方向振动和试验频响曲线对比

图4 Y方向振动和试验频响曲线对比

图5 Z方向振动和试验频响曲线对比

从3个方向振动试验和仿真加速度频响曲线对比可见,3个方向仿真和试验频响曲线趋势相对一致,其中X向偏差相对较大,Y、Z向吻合较好。仿真1和仿真2是阻尼比分别为0.01、0.02下的曲线,阻尼比对系统振动加速度幅值有一定影响,阻尼比越大振幅越小。得到壳体结构第一阶频率为186.85 Hz,最大响应73.2g。总结可知,仿真结果有一定的精度,测点的加速度与试验结果有一定偏差,这与整体结构装配边界模拟、各部件连接特性以及阻尼设定有关,同时由于仿真计算基于线性假设,而实际试验时结构接触间难免会出现一定程度的非线性,这就难以保证仿真和试验保持一致。

3 结构优化设计

该调节器壳体在正弦振动试验时,其壳体在Z向振动试验阶段底部出现壳体开裂,振动开裂部位位于图1圈中所示部位。由于该壳体结构较长,底部固定后形成较大悬臂结构,同时因内部油路和减重需要,在底部中间部位存在较大挖空设计,这影响了壳体底部抵抗变形的刚度,造成壳体在外部载荷作用下激发出较大的振动,靠近底部的尖角部分承受了较大振动应力,容易发生破坏。

为了改善调节器壳体在工作过程中的振动性能,需要提升其最大加速度部位后端的刚度,减小壳体振动加速度。因此在控制整体重量的前提下,结合标定完成的有限元模型,对加速度较大的部位进行针对性的多方案优化分析。

优化方向主要从两方面考虑:一是提高壳体薄弱部位的刚度,采取的措施如设置加强筋、增加壁厚、减少破坏结构连续的孔洞;二是尽量降低整体结构重心,调整功能布局,减少悬臂效应。

对优化前后两种壳体结构做了谐响应分析对比,优化前后6阶固有频率对比如表1所示。对出现故障的Z向谐响应振动,调节器壳体改进前后Z向正弦振动仿真应力云图如图6所示。从表1中对比可以看出,优化后壳体前6阶频率都有很大的提高,1阶提高了26.9%。出现壳体开裂的Z向受载时进行正弦振动仿真分析,优化前壳体等效应力云图显示最大应力为182.02 MPa,其余部位应力值相对较小,从图中可以直观看出试验件上的应力的最大位置位于壳体底部转角处,这与实际开裂部位一致;其主要原因为电气部位的薄壁腔承担了类似加强筋的作用,处于壳体的主要承力部位,由于该薄壁腔自身强度不足,导致在振动试验中产生裂纹。优化设计中,将壳体的电气腔远离承力部位,避免电气腔的薄壁结构出现应力集中的情况,以提高产品的强度能力。优化后的振动等效应力云图也显示壳体整体振动应力得到降低。

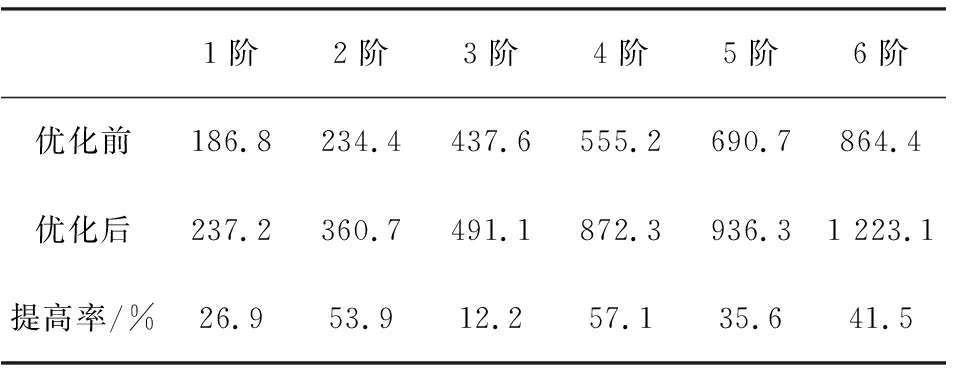
表1 优化前后6阶固有频率对比(Hz)

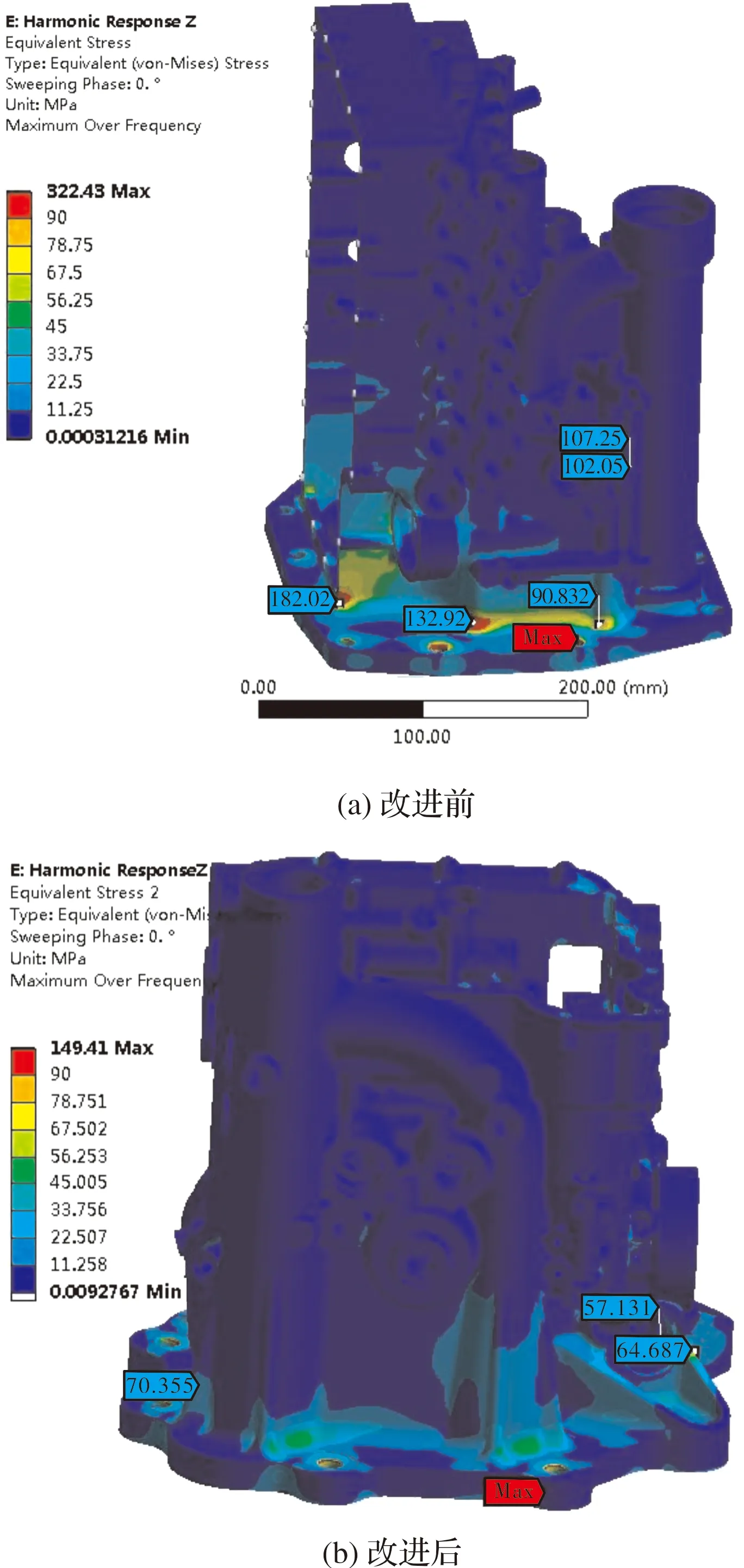
图6 调节器壳体改进前后Z向正弦振动仿真应力云图

4 结论

通过对调节器组件谐响应振动试验的仿真分析,并与真实试验结果进行对比修正,印证了壳体开裂的试验现象,找出了壳体振动失效机理和改进方向;借助仿真对改进件的响应峰值频率及振动应力大小进行预测,使设计结果可视化,有助于设计人员对产品进行优化,改进后的新壳体底部设置加强筋的结构形式及调整功能布局、降低整体高度,重量减轻,经仿真分析及试验验证,结构强度富裕,抗振能力得到提高。