立体几何初步常见典型考题赏析
2023-04-25■何伟
■何 伟
立体几何中的概念、公理、定理是同学们需要掌握的核心知识。下面就空间几何体的结构特征、简单几何体的表面积与体积、空间点线面的位置关系,以及直线、平面的平行和垂直关系,进行举例分析,供同学们参考。
题型一:空间几何体的结构特征、表面积和体积
掌握空间几何体的结构特征,灵活运用几何体的表面积、体积公式是解答这类问题的关键。多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理;旋转体的表面积注意其侧面展开图的应用;求复杂几何体的体积常用割补法、等积法。
例1学生到工厂劳动实践,利用3D 打印技术制作模型,如图1,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6cm,AA1=4cm,3D 打印所用原料密度为0.9g/cm3。不考虑打印损耗,制作该模型所需原料的质量为_____g。12(cm3),所以该模型的体积为144-12=132(cm3),所以制作该模型所需原料的质量为132×0.9=118.8(g)。
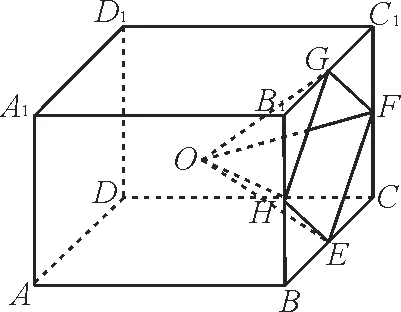
图1

跟踪训练1:如图2 所示,已知三棱柱ABC-A′B′C′,侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,求三棱柱ABC-A′B′C′的体积。
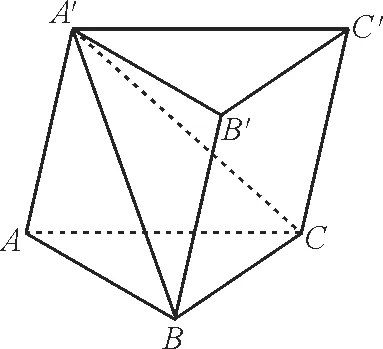
图2

题型二:与球有关的切、接问题
与球相关问题的解题策略:作适当的截面(如轴截面等),对于球内接长方体或正方体,则截面一要过球心,二要过长方体或正方体的两条体对角线,才有利于解题;对于“内切”和“外接”问题,首先要弄清几何体之间的相互关系,主要是弄清特殊的点线面之间的关系,然后把相关的元素放到这些关系中来解决。
例2设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9 3,则三棱锥D-ABC体积的最

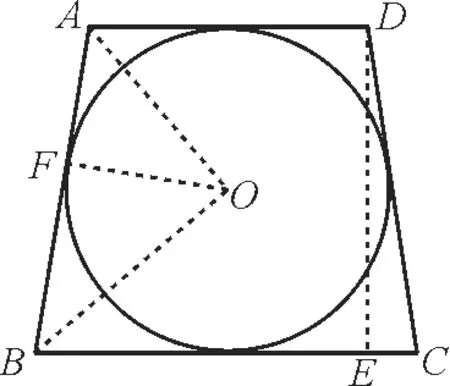
图3
设球的半径为r1。在Rt △CDE中,DE=2r1,CE=R-r,DC=R+r。
由勾股定理得4r21=(R+r)2-(Rr)2,解得r1=,故球的表面积S球=4πr21=4πRr。
(方法2)设球心为O,球的半径为r1。在Rt△AOB中,OF是斜边AB上的高。由相似三角形的性质得OF2=BF·AF=Rr,即r21=Rr,解得r1=。故球的表面积S球=4πRr。
题型三:空间角的计算问题
求空间各种角的大小一般都转化为平面角来计算,求空间角的计算步骤:一作,二证,三计算。求异面直线所成的角,常用平移转化法(即转化为相交直线的夹角);求直线与平面所成的角,常用射影转化法(即作垂线、找射影)。二面角的平面角的作法常有三种,即定义法,垂线法,垂面法。
例3如图4,在三棱台ABC-DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC。
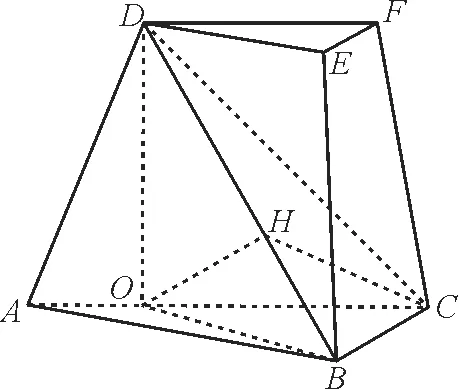
图4
(1)证明:EF⊥DB。
(2)求直线DF与平面DBC所成角的正弦值。

跟踪训练3:如图5 所示,已知正方体ABCD-A′B′C′D′的棱长为1,B′C∩BC′=O。
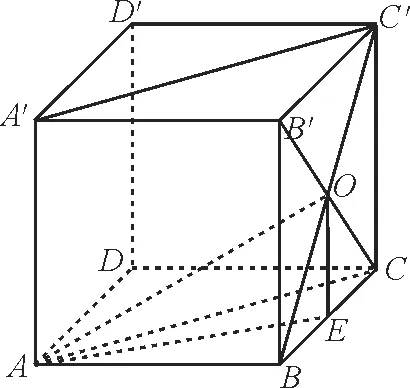
图5
求:(1)AO与A′C′所成角的大小。
(2)AO与平面ABCD所成角的正切值。
(3)平面AOB与平面AOC所成角的大小。

题型四:平面的基本性质
点线确定平面的条件:由点确定平面,即三点不共线;由点和线确定平面,即点不在直线上;由线确定平面,即两条相交线、两条平行线。证明点或线共面的两种方法:由所给条件中的部分线(或点)确定一个平面,然后证其余的线(或点)在这个平面内;将所有条件分为两部分,然后分别确定平面,再证两平面重合。证明点共线的两种方法:先由两点确定一条直线,再证其他各点都在这条直线上;直接证明这些点都在同一条特定的直线上。证明线共点的方法:先证其中两条直线交于一点,再证其他直线经过该点。

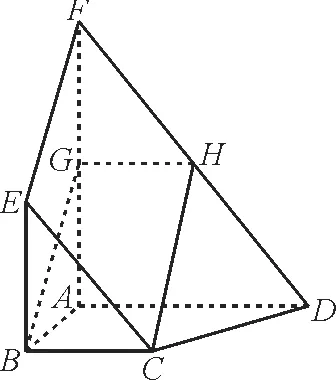
图6

跟踪训练4:如图7 所示,在正方体ABCD-A1B1C1D1中,E,F分 别 是AB和AA1的中点。
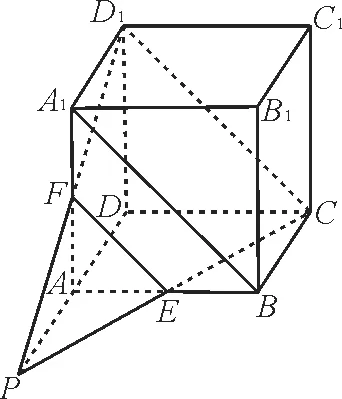
图7
求证:CE,D1F,DA三线共点。
提示:连接EF,CD1,A1B。由EF//CD1,EF<CD1,可得CE与D1F必相交,设交点为P。由P∈CE,CE⊂平面ABCD,可得P∈平面ABCD。
同理可得,P∈平面ADD1A1。又平面ABCD∩平面ADD1A1=DA,所以P∈直线DA,所以CE,D1F,DA三线共点。
题型五:线面、面面平行关系的应用
根据两平行直线确定一个平面,可以证明共面问题,其实质是证明直线平行。线面平行的判定定理是由线线平行得到线面平行,性质定理是由线面平行得到线线平行,因此线线平行与线面平行可以相互转化,也体现了平面和空间平行关系的相互转化。关于平行条件的探究:根据面面平行的性质得出交线互相平行,从而可以确定交线的位置,进而作出交线,这是面面平行性质的典型应用;线面平行时,一是寻找与面内直线平行的直线,二是构造平行平面,那么平面内任意直线与另一个平面平行。
例5如图8,在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的平面是_____。
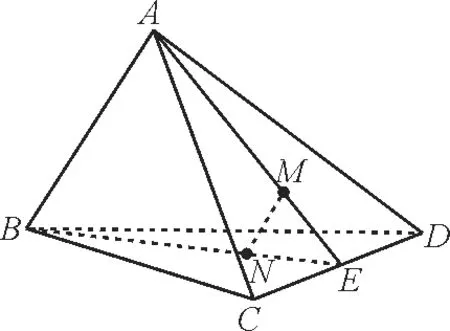
图8
解:取CD的中点E,则EM∶MA=1∶2,EN∶BN=1∶2,所以MN//AB。因为MN⊄平面ABD,MN⊄平面ABC,AB⊂平面ABD,AB⊂平面ABC,所以MN//平面ABD,MN//平面ABC。
跟踪训练5:如图9 所示,在直三棱柱ABC-A1B1C1中,D为AA1中点,点P在侧棱CC1上运动,当点P满足条件_____时,A1P//平面BCD。
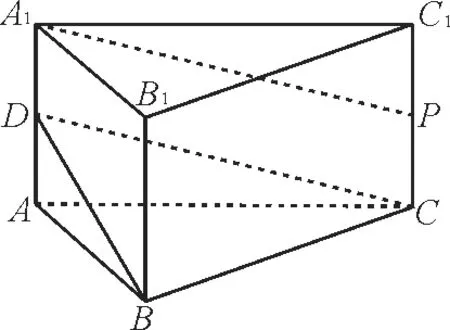
图9
提示:取CC1的中点P。在直三棱柱ABC-A1B1C1中,D为AA1中点,点P在侧棱CC1上运动,所以当点P是CC1的中点时,A1P//CD。因为A1P⊄平面BCD,CD⊂平面BCD,所以A1P//平面BCD。答案为点P是CC1的中点。
题型六:线面、面面垂直关系的应用
证明线面垂直的思路与方法:分析已知的垂直关系,得出能够推出的线线、线面垂直,即挖掘已知条件,以方便后续证明;证明垂直关系时往往需要采用逆向思维,如证明直线a垂直于平面α内直线b,可考虑证明直线b垂直于直线a所在的平面β;掌握线线、线面垂直的相互转化。证明面面垂直,只需证明线面垂直,即在其中一个平面内寻找一条直线与另一个平面垂直,这是证明面面垂直的常用方法。定义法证明面面垂直:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。熟练掌握线线垂直、线面垂直、面面垂直之间的相互转化是解题的常规思路,垂直关系证明的核心是线面垂直,准确找到要证明的直线是关键,再利用线线垂直进行证明。
例6如图10所示,在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1。
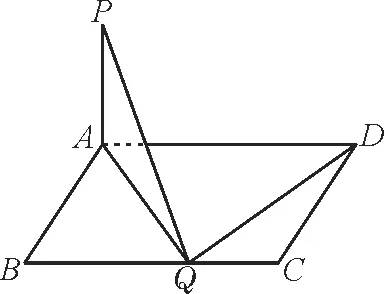
图10
(1)若BC边上恰有一点Q,使得PQ⊥QD,则a的取值是____。
(2)若BC边 上 存 在 点Q,使 得PQ⊥QD,则a的取值范围是____。
解:利用以AD为直径的圆与BC的关系解题。因为PA⊥平面ABCD,QD⊂平面ABCD,所以PA⊥QD。又因为PQ⊥QD,PA∩PQ=P,所以QD⊥平面PAQ,所以AQ⊥QD。
(1)当a=2时,以AD为直径的圆与BC相切于BC的中点Q,此时∠AQD=90°,所以BC边上存在一点Q,使得PQ⊥QD。故所求a=2。
(2)当a>2时,以AD为直径的圆与BC相交于点Q1,Q2,此时∠AQ1D=∠AQ2D=90°,故BC边上存在两点Q(即Q1与Q2),使PQ⊥QD,所以a≥2,即a∈[2,+∞)。
跟踪训练6:如图11 所示,平面四边形ABCD中,AB=AD=CD=1,BD= 2,BD⊥CD,将其沿对角线BD折成四面体A-BCD(如图12),使平面ABD⊥平面BCD,则下列说法中不正确的是( )。
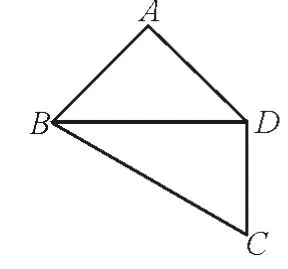
图11
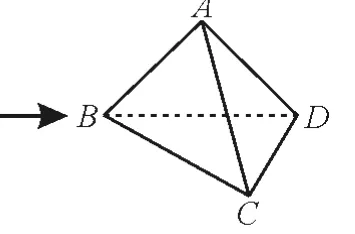
图12
A.平面ACD⊥平面ABD
C.平面ABC⊥平面ACD
D.AD⊥平面ABC
提示:对于A,因为平面ABD⊥平面BCD,平 面ABD∩平 面BCD=BD,BD⊥CD,所以CD⊥平面ABD,所以平面ACD⊥平面ABD,A 正确。对于B,CD⊥平面ABD,AB⊂平面ABD,所以AB⊥CD,B 正确。对于C,易得AB⊥AD,AB⊥CD,又AD∩CD=D,所以AB⊥平面ACD,所以平面ABC⊥平面ACD,C 正确。对于D,若AD⊥平面ABC,则AD⊥AC,这时与CD⊥AD矛盾,D 错误。应选D。
题型七:点到平面的距离问题
高考对立体几何的考查主要有两个方面,一是探究空间直线、平面的平行与垂直关系;二是与计算有关的综合性问题。点到平面的距离问题是高考的常考题型。

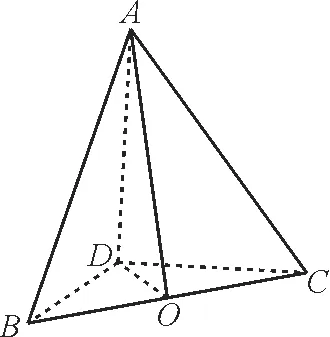
图13

题型八:探索性问题
对命题条件的探索常采用三种方法:先猜后证,即先观察与尝试给出条件再证明;先通过命题成立的必要条件探索出命题成立的条件,再证明其充分性;把几何问题转化为代数问题,探索命题成立的条件。对命题结论探索的常用方法:首先假设结论存在,然后在这个假设下进行推理论证,如果通过推理得到了合乎情理的结论,就肯定假设,如果得到了矛盾的结论,就否定假设。
例8如图14 所示,在正方体ABCDA1B1C1D1中,O为底面ABCD的中点,P是DD1的中点,设Q是CC1上的点,当平面D1BQ//平面PAO时,则点Q( )。
在回家的路上,我们又看到奇特的一幕。天空出现了微红的太阳。阳光洒在高速公路两旁的大树上,让那些秋叶更加金黄。我想,就用这秋叶代替那红罂粟,献给曾为国家民族做出过贡献的人们。于是,我口占一首七言绝句。诗云:
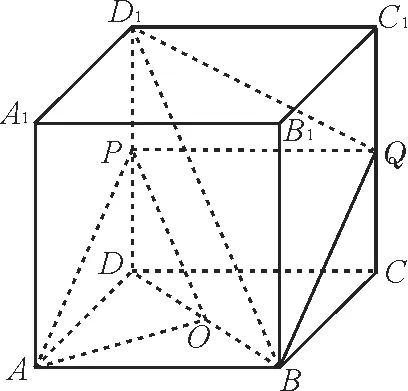
图14
A.与C重合
B.与C1重合
C.为CC1的三等分点
D.为CC1的中点
解:在正方体ABCD-A1B1C1D1中,由O为底面ABCD的中心,P是DD1的中点,可得PO//BD1。当点Q为CC1的中点时,则PQ■AB,可知四边形ABQP是平行四边形,所以AP//BQ。由AP∩PO=P,BQ∩BD1=B,可得平面D1BQ//平面PAO。应选D。
跟踪训练8:如图15所示,一张A4纸的长、宽分别为2 2a、2a,A,B,C,D分别是其四条边的中点。
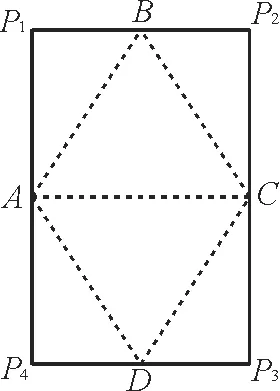
图15
现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体。下列关于该多面体的命题,正确的是____。(写出所有正确命题的序号)
①该多面体是三棱锥;②平面BAD⊥平面BCD;③平面BAC⊥平面ACD;④该多面体外接球的表面积为5πa2。
提示:由(2a)2+(2a)2=4a2,可知该多面体是以A,B,C,D为顶点的三棱锥,点P在棱BD上,如图16,①正确。
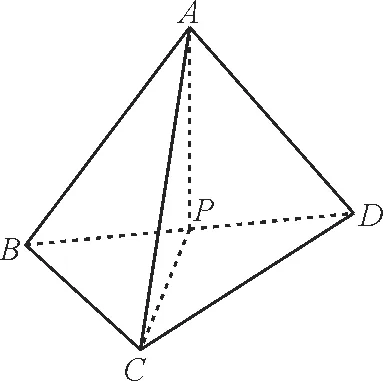
图16
由AP⊥BP,AP⊥CP,BP∩CP=P,可得AP⊥平面BCD。由AP⊂平面BAD,可得平面BAD⊥平面BCD,②正确。同理可证,平面BAC⊥平面ACD,③正确。通过构造长方体可得该多面体的外接球半径R=,所以该多面体外接球的表面积为5πa2,④正确。正确的序号为①②③④。
题型九:最值问题
有关空间几何体最值问题的两种求法:观察图形特征,确定取得最值的条件,计算出最值;设出未知量,建立函数关系,利用基本不等式求出最值。
例9如图17,已知长方体ABCDA1B1C1D1的体积V=12,AB=2,若四面体A-B1CD1的外接球的表面积为S,则S的最小值为( )。
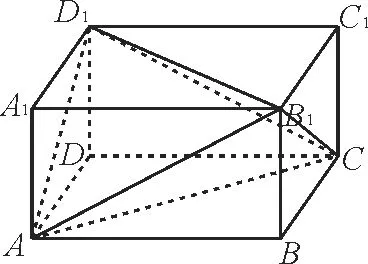
图17
A.8π B.9π C.16π D.32π
解:设BC=x,BB1=y。由于V=12,

跟踪训练9:(1)若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值为_____(只需写一个可能值)。
(2)四面体ABCD中,AC⊥AD,AB=2AC=4,BC=2 5,AD=2 2,当四面体的体积最大时,其外接球的表面积是_____。
提示:(1)由题意可构造出两类满足条件的四面体:五条边长为2,另一边长为1,或对棱相等的四面体。四面体ABCD,如图18。
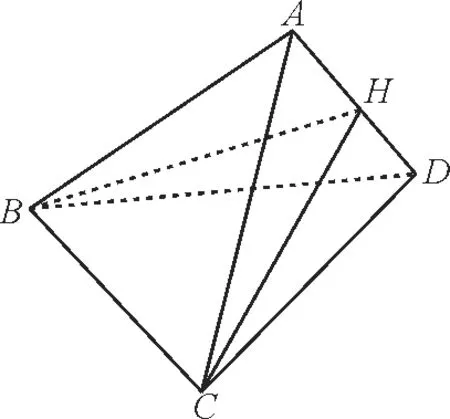
图18

感悟与提高
1.如图19,四边形ABCD和四边形ADPQ均为正方形,它们所在的平面互相垂直,则异面直线AP与BD所成的角为_____。
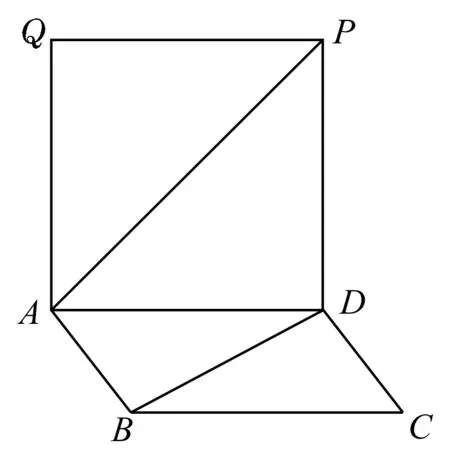
图19
提示:由题意可将原图补成正方体ABCD-QGHP(图 略),连 接GP,则GP//BD,所以∠APG为异面直线AP与BD所成的角。在△AGP中,因为AG=GP=AP,所以∠APG=。
2.如图20 所示,P为平行四边形ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD∩平面PBC=l。
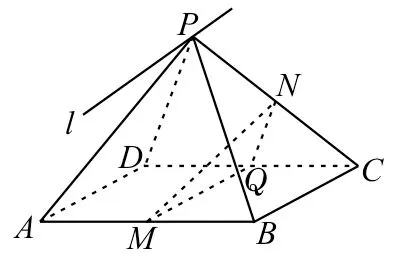
图20
(1)判断BC与l的位置关系,并证明你的结论。
(2)判断MN与平面PAD的位置关系,并证明你的结论。
提示:(1)结论:BC//l。
因为AD//BC,BC⊄平面PAD,AD⊂平面PAD,所以BC//平面PAD。
又BC⊂平面PBC,平面PAD∩平面PBC=l,所以BC//l。
(2)结论:MN//平面PAD。
取CD的中点Q,连接NQ,MQ,MN,则NQ//PD,MQ//AD。因为NQ∩MQ=Q,PD∩AD=D,所 以 平 面MNQ//平 面PAD。又 因 为MN⊂平 面MNQ,所 以MN//平面PAD。
