立体几何中轨迹问题的处理技巧与方法

■陈 婷

立体几何中的轨迹问题,是立体几何与解析几何的知识交汇点。这类问题,立意新颖,重视不同知识的交叉与渗透,重视对数学知识与数学能力的考查与应用,是培养同学们数学核心素养的好素材。

一、直接法

直接法就是直接利用立体几何的相关知识,合理分析和研究问题中各个元素之间的关系,或者直接利用轨迹定义进行求解的方法。

例1如图1,在正方体ABCD-A1B1C1D1中,P是侧面BCC1B1上的一个动点,若点P到直线BC与直线C1D1的距离相等,则动点P的轨迹是下列哪种线的一部分( )。

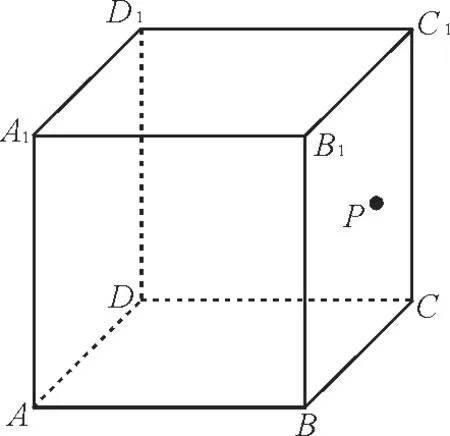
图1

A.直线 B.圆

C.双曲线 D.抛物线

分析：根据题设条件,利用空间点线面的位置关系,直接得到动点P到直线BC与到点C1的距离相等,再结合解析几何中抛物线的定义,可得对应的答案。

解：根据正方体的性质,可知C1D1⊥平面BCC1B1,所以动点P到直线C1D1的距离与到点C1的距离相等。又动点P到直线BC与到直线C1D1的距离相等,所以动点P到直线BC与到点C1的距离相等。根据抛物线的定义,可得动点P的轨迹是一条抛物线的一部分。应选D。

二、转化法

转化法就是将立体几何问题转化为平面几何问题,进行合理“降维”处理,进而应用平面几何、解析几何等相关知识来分析与求解的方法。

例2(2022年高考北京卷)已知正三棱锥P-ABC的六条棱长均为6,S是△ABC及其内部的点构成的集合。设集合T={Q∈S|PQ≤5},则T表示的区域的面积为( )。

三、解析法

解析法就是利用解析几何在研究轨迹方面的一整套比较完整的理论体系,通过坐标法进行代数运算与逻辑推理的一种求轨迹的方法。解析法是解决立体几何图形的二维轨迹问题的常用方法之一。

例3(多选题)如图2 所示,在正方体ABCD-A1B1C1D1中,E是CC1的 中 点,点P在底面ABCD内运动,若PD1,PE与底面ABCD所成的角相等,则动点P的轨迹是( )。

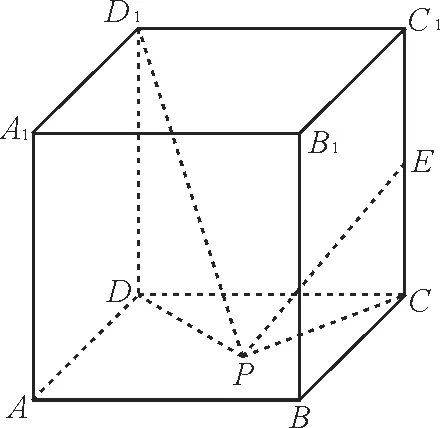
图2

A.圆的一部分

B.椭圆的一部分

C.经过线段BC靠近B的三等分点

D.经过线段CD靠近C的三等分点

分析：根据题意得DP=2PC,以点D为坐标原点,建立平面直角坐标系,通过坐标法进行讨论求解。

解：由正方体的性质得DD1⊥平面ABCD,EC⊥平 面ABCD,所 以∠DPD1,∠CPE分别为PD1,PE与底面ABCD所成的角,所以∠DPD1=∠CPE。

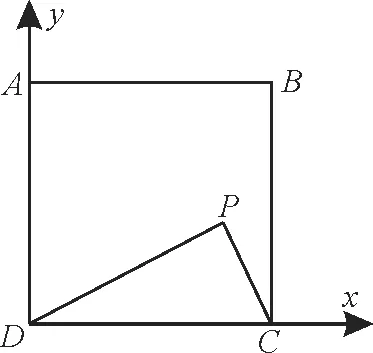
图3

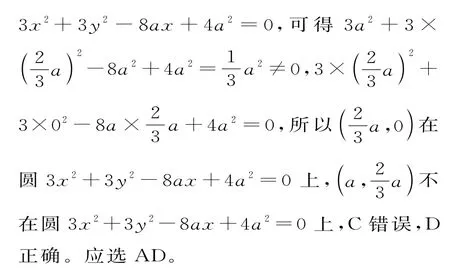
四、性质法

性质法就是利用轨迹的相关知识来解决立体几何中轨迹问题的一种基本方法。有些空间图形的轨迹不一定是二维的,转化为平面问题比较困难,这时可借助性质法来处理。

例4已知棱长为3 的正方体ABCDA1B1C1D1中,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则线段MN的中点P的轨迹与正方体的面所围成的几何体的体积为____。

分析：不论△MDN如何变化,点P到点D的距离始终等于1。从而点P的轨迹是一个以点D为球心,半径为1 的球的,由此可求出体积。

解：如图4 所示,端点N在正方形ABCD内运动。

图4