一种基于蜂群优化算法的ICA-R 算法
2023-04-19张守成
张守成
(广西民族师范学院 数理与电子信息工程学院, 广西 崇左 532200)
0 引 言
独 立 分 量 分 析 ( Independent Component Analysis,ICA)是20 世纪90 年代后期发展起来的一项新的信号分解技术,目前已成功应用在语音分析、特征提取、生物医学工程等领域[1-2]。 传统ICA 方法以分离出所有源信号为目标,往往同时分离出所有的源信号[3-6],而在很多实际应用中,可能仅对其中某一个源信号感兴趣。
在此背景下,Lu 等学者[7-8]提出了参考独立成分分析(ICA-R)算法,利用期望提取信号的波形先验信息构造出参考信号,将其引入到传统的ICA 算法中,通过优化算法提取出在一定量度下与参考信号最接近的输出作为期望源信号,具有直接高效的优点,并且参考信号的引入能提高期望源信号的分离质量和精度。 但该方法计算相对繁琐。 本文通过对ICA-R 算法的原理进行分析,利用峭度作为度量,巧妙调整目标函数,并利用蜂群优化算法处理目标函数,得到一种计算简单、分离性能好的ICA-R算法。 最后通过仿真实验证明了该算法的有效性。
1 蜂群优化算法
德国生物学家Frisch 发现在自然界中,虽然各组织内不同职能的蜜蜂只能完成单一的任务,但蜜蜂通过摇摆舞、气味等多种信息交流方式,使得整个蜂群能够迅捷地发现优良蜜源,实现自组织行为[9]。 Seeley 在1995 年最先提出了蜂群的自组织模拟模型;Teodorovic 于2003 年进一步提出了蜂群优化算法(Artificial Bee Colony, ABC)[10-12]。 ABC算法是一种新兴的仿生智能优化算法,具有全局收敛能力强、设置参数少、适用范围广等特点,ABC 已被应用于许多科学工程领域。 例如,文献[11]将ABC 算法应用于盲信号分离代替了传统的梯度法,克服了梯度法收敛速度慢、易陷入局部极值点等缺点,提高了盲源分离算法的分离精度和稳定性。
2 基于蜂群优化算法的ICA-R 算法
线性瞬时混合ICA 模型通常表示为[1]:x(t)=As(t),其中s(t)=[s1(t),…,sM(t)]T是M个假设为统计独立的未知源信号,A是一个未知的N × M混 合 矩 阵 ( 一 般 假 设N≥M),x t( )=[x1(t) ,…,xN(t) ]T是源信号经A线性混合后得到的N个观测信号。
ICA 的目标是估计一个最佳的M × N解混矩阵W,使得观测信号经过W变换后得到的M个输出信号y(t)=Wx(t) 是独立的,从而作为源信号s(t)的估计。 一般情况下不可能直接求得解混矩阵的解,需要通过基于目标函数的自适应方法求解,具体过程是:首先对实际问题的源信号和信道传输过程进行分析,然后根据源信号的随机特征确定度量输出源分离结果的测度,如非高斯性、稀疏性等测度方法,根据测度理论构造目标函数,并选择合适的优化方法。 常用的优化算法有基于梯度的随机梯度算法和牛顿方法等。 在进行优化后,最终获得解混矩阵,输出估计的源信号。 因此ICA 的核心问题可以表示为:ICA 方法=目标函数+优化算法[12]。
而ICA-R 算法一般利用期望源信号的波形先验信息构造出其参考信号r(t), 随后将输出信号y(t) 与r(t) 的某个接近性量度ε(y,r) 作为先验约束引入到传统ICA 的学习中,算法收敛后得到一个最优权向量w*(解混矩阵W的一行),将y =w*Tx(t) 作为期望源信号的估计信号。
以上就是ICA-R 算法的基本原理,文献[7]选择负熵作为信号非高斯性的度量,并据此构造目标函数,利用拟牛顿方法得到了一种ICA-R 算法。 但由于涉及复杂的二阶导数计算,效率较低。
峭度作为信号非高斯性的度量也被广泛使用,基于ICA-R 算法的原理,本文选取输出信号峭度的绝对值作为输出信号非高斯型的度量,假定K(y) 有M个局部或全局最优解wi(i=1,…,M),相应给出M个源信号的估计。 则输出信号与参考信号的接近性量度ε(y,r)当且仅当输出y =w*Tx是期望源信号时取得最小值,即有:
由此可知,一定存在一个阈值参数ξ满足以下不等式, 当且仅当输出信号y =w*Tx时使得g(w)=ε(y,r) -ξ≤0 成立。 将g(w) ≤0 作为一个对K(y) 的约束,则算法的优化框架为:
(1)最大化。 研究推得的公式为:
(2)约束。 研究推得的公式为:
其中,等式约束h(w)=0 用于保证K(y) 和w有界。
将观测数据x进行白化,用表示白化后数据,并对权向量w每次更新后归一化。 则有E(y2)=,其中R~x~x =I是的协方差矩阵。 上式保证了h(w)=E(y2) - 1=0恒成立,从而算法的优化框架简化为:
(1)最大化。 研究推得的公式为:
(2)约束。 研究推得的公式为:
由ICA-R 算法设计的基本原理可知,在约束g(w) ≤0 下最大化得到最优权向量w*, 此时接近性量度ε(y,r) 也取得最小值,则- ε(y,r) 取得最大值,从而可将最大化的目标函数调整为K(y) 和- ε(y,r) 的乘积,即:
其中,ε(y,r)=E[(y - r)2]。
通过最大化M(y) 得到最优权向量w*的优化算法选择较多,鉴于ABC 算法具有全局收敛性强、收敛速度快的特点,采用ABC 算法对目标函数M(y) 进行优化得到最优权向量w*,就可以实现目标源信号的提取。
3 仿真实验与性能分析
为了验证本文改进算法的有效性,对合成数据进行仿真实验。取4 个零均值单位方差的独立源信号:S1,S2为确定性信号,S3,S4为随机信号。 样本数据为2 000个,经白化后的源信号如图1 所示(为方便观察,只绘出前300 个样本点)。 用一个随机生成的高斯矩阵对源信号进行混合,得到的混合信号如图2 所示。 用各源信号相应的符号函数序列作为提取的对应参考信号,如图3 所示。 采用本文所提算法对各源信号进行抽取,收敛后抽取的信号如图4 所示。 直观上比较图4 与图1,波形基本一致,表明算法很好地实现了对各个信号的盲抽取。

图1 源信号Fig. 1 Source signal

图2 混合信号Fig. 2 Mixed signal
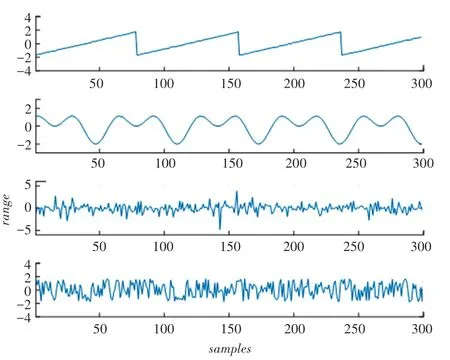
图4 抽取信号Fig. 4 Extracted signal
为进一步说明分离效果,采用量化指标IPI(Individual Performance Index)对分离性能进行评价[1]:
其中,pj表示全局分离变量p =wTA的第j个元素。IPI越接近于零,表明算法分离性能越好。
对上述信号采用本文算法进行150 次蒙特卡洛实验,每次都随机产生混合矩阵。 实验结果显示,算法每次都能抽取成功,表明算法在不需要阈值参数选择的情况下收敛性能稳定。
150 次提取信号后的平均IPI值见表1。

表1 算法收敛的平均IPI 值Tab. 1 Average IPI of the algorithm
表1 显示在成功抽取时采用本文算法有低IPI值,说明算法对各源信号的抽取性能优异。
4 结束语
通过巧妙调整目标函数并采用蜂群优化算法有效避免了阈值选择问题,简化了计算。 计算机仿真实验表明了本文算法收敛性能稳定,可有效实现对信号的盲提取。 当然,对实际应用中不同的提取信号,如何构造合适的参考信号是需要进一步探讨的课题。
