基于降阶模型和梯度优化的流场加速收敛方法

曹文博，刘溢浪，张伟伟

西北工业大学 航空学院，西安 710072

计算流体力学（Computational Fluid Dynamics，CFD）在近40 年的时间内发展迅速，成为流体力学理论研究及工程气动设计和分析的重要手段。如今，科学研究以及工程问题的日益复杂化和精细化给CFD 算法的效率提出了更高要求。因此，发展高效的加速收敛方法仍是计算流体力学中至关重要的研究方向。

迄今为止，研究者已提出了许多经典的加速收敛算法，例如局部时间步长、隐式残差光顺[1］、多重网格[2］、焓阻尼方法[3］、低马赫数预处理[4］等。最小化迭代求解器收敛残差外插方法的一般过程是根据迭代求解过程中解快照外插得到残差更小的解，而后基于该预测值继续迭代求解生成新的解快照，以此循环。其优势在于应用简单，不必修改求解器算法，并能和经典加速收敛算法结合使用。

早期的外插方法几乎都是基于线性迭代假设xj+1=Axj+b（其中A、b 未知），通过迭代过程中的解快照{ xn}近似该系统解s：s=As+b。这些方法主要分为2 大类：①epsilon 算法；②多项式方法。向量epsilon 算法[5］（Vector Epsilon Algorithm，VEA）和拓扑epsilon 算法[6］（Topological Epsilon Algorithm，TEA）是最早的外插方法，其借助求和方法和一些复杂的反演公式将缓慢收敛的序列转化为快速收敛的序列，但这类方法的复杂性使得其应用较困难。多项式是一种更简单的外插方法，最小多项式外插[7］（Minimal Polynomial Extrapolation，MPE）和降阶外插[8-9］（Reduced Rank Extrapolation，RRE）是其中主要的2 种方法。这些方法的比较可见Smith 等[10］的综 述。Sidi[11］阐 述 了MPE、RRE 方 法 与Arnoldi方法[12］和GMRES 方法[13］的联系。这些方法之后被发展并应用于Euler 方程和其他迭代求解器的加速求解[11，14］。Djeddi 等[15］假设迭代线性收敛，将方程残值表示为解的线性函数R(U )≈AU-b，并结合降阶模型近似该系统的解，实现了雷诺平均Navier-Stokes 方程（Reynlods-Averaged Navier-Stokes，RANS）的加速收敛。

随 着 动 态 模 态 分 解[16-17］（Dynamic Mode Decom-position，DMD）成为流场分析的热点，基于DMD 外插方法也引起了研究者的兴趣。Liu等[18］使用DMD 预测双时间步格式中内迭代的初始条件从而加速RANS 方程求解。Andersson[19］使用DMD 预测了线性迭代假设下的收敛解。另外，基于DMD 的模态多重网格（Mode Multigrid，MMG）[20-21］也被验证是一种有效的加速收敛方法，这种方法认为DMD 一阶模态对应于稳态流动，使用DMD 过滤振荡模态以加速收敛。

降阶模型（Reduced-Order Model，ROM）外插是另外一种以较小计算成本获得合理外插结果的方法。基于POD 的降阶模型算法是近30 年发展起来的，它将高维控制方程转化为给定POD模态下的一组低阶方程，从而极大地减少了计算时间，该方法已广泛应用于各种领域[22-26］。然而，由于该方法需要用高保真的方法（通常是髙耗时的CFD 计算）预先获取流场快照，早期这类方法只应用于有较多变化参数且需要多次重复求解的CFD 问题。后来，基于POD 的降阶模型被发展并应用于全隐式求解器中内迭代过程的初值预测，从而加速了非定常问题求解[27-29］。这些方法中，流场快照不是预先给定的，而是在非定常时间推进求解过程中收集并不断被更新，避免了已有工作[22-26］中预先计算流场快照带来的昂贵代价，但这些加速方法均局限于隐式求解器。之后，Rapun 等[30］提出了当地POD 方法用于加速抛物型问题的非定常求解过程，该方法使用数值格式和降阶模型交替求解方程，并通过对降阶模型近似误差的先验估计确定降阶模型的求解时长，保证了鲁棒性和有效性，并被应用于各类稳态[31］和瞬态[32-34］流动的加速求解。

基于POD 降阶模型尽管已经被应用于一些方程的加速求解，但CFD 算法的复杂性，特别是基于非结构网格有限体积法的复杂性，且CFD 求解器构造对应的嵌入式降阶模型较为困难，因此，该类方法并未被应用于复杂问题的RANS 方程加速求解。本文对已有方法进行了多种改进，使得降阶模型中只包含关于流场快照的简单代数运算，形成了一个加速RANS 方程稳态求解过程的通用框架。具体的改进主要包括：①流场快照中不仅包含网格格心处的流场值，还包含有限体积法离散格式中需要计算的面心流场值、面心左右两侧的流场值、面心流场梯度，避免了对POD 模态的空间离散；②不将控制方程转化为常微分方程组而后时间推进求解，取而代之的是通过梯度优化寻找POD 子空间内残差最小解，这种方法具有更强的灵活性和鲁棒性；③只计算少量网格残值来优化模态系数从而大大减少降阶模型优化求解的计算成本。

1 数值方法

1.1 控制方程

考虑了基于SA 湍流模型的二维雷诺平均Navier-Stokes方程。RANS 方程组的积分形式为

式 中：V=[ux，uy]T为 流 体 运 动 速 度；Ω 为 控 制体，其边界为∂Ω；n 为边界的单位外法G(Q)线方向；Q 为守恒变量；F(Q)为无黏通量；G(Q)为黏性通量；ρ、e0、P、T 分别为流体的密度、单位体积的总能、压强和温度；nx、ny分别为边界外法线方向n 在x、y 方 向 的 分 量；σij为 流 体 间 的 应 力，i 为作用面的方向，j 为作用方向；qj为单位质量的体积热在3 个方向上的分布；γ 为气体的比热比，对于理想气体γ=1.4；μ 为分子黏性系数，可利用Sutherland 公式得到，即

μt为湍流黏性系数，通过求解湍流模型或亚格子模型方程得到；传热项中Pr 为层流Prandtl 数，Prt为湍流Prandtl 数，文中分别取值为0.87 和0.9。

对于理想气体，有

由于SA 方程的复杂性，本文不对SA 方程做降阶处理，即求解降阶模型时涡黏固定不变。

1.2 数值格式

有限体积法中，控制方程通常被离散为数值形式：

式中：m 为网格编号；Vm为网格m 的体积；Qm为网格m 格心处的守恒变量；F(m)为网格m 拥有的面的集合；p 为面的编号；Ump、∇Ump、ULmp、URmp分别为面心处的流场值、流场梯度、面心左侧的流场值、面心右侧的流场值；ΔSmp为面积分别为面心无黏通量和黏性通量，可采用不同的通量格式求解。

1.3 基于POD 的降阶模型

降阶模型用于将控制方程转化为给定POD模态下的低阶常微分方程组，从而极大地减少了计算时间。首先收集CFD 计算得到的流场快照X=[U1，U2，…，UN]，对其进行奇异值分解得到POD 模态（通常对奇异值较小的模态截断）。

在本文中，将构建N-S 方程的降阶模型，实现加速收敛目的，降阶模型的数值格式必须与CFD 一致，因此将基于有限体积法的数值格式式（8）投 影 到 POD 模 式 上 。 注 意 到Ump、∇Ump、ULmp、URmp均为不同网格格心值Um的线性叠加，且POD 快照均为流场快照的线性叠加，若

式 中：Xm、Xmp、X∇mp、XLmp、XRmp和 Φm、Φmp、Φ∇mp、ΦLmp、ΦRmp分 别 为Um、Ump、∇Ump、ULmp、URmp的 流 场快照和POD 模态。式（16）表明，仅需对格心流场值Um做POD 分析，其余变量的POD 模态均可以通过式（16）得到，其中T 通过式（17）计算：

通过式（16）和式（17）计算得到POD 模态后，则可得到Galerkin 展开式为

1.4 梯度优化方法

梯度下降是一种用来最小化目标函数R(ξ)的方法，根据目标函数对参数ξ 的负梯度-∇R(ξ)以给定学习率ε 更新参数的值。

文中，降阶模型部分在Python 中实现，使用自动微分计算梯度∇R(ξ)，使用AdamW 算法进行梯度优化。特别地，最后一个流场快照对应的模态系数显然较逼近最优解，因此可将其作为优化参数的初值ξ0以加速优化过程。

需要注意的是，尽管相比于CFD，降阶模型采用式（18）计算Ump、∇Ump、ULmp、URmp减少了计算量，但由于降阶模型是使用梯度优化求解，降阶模型求解的计算量仍会较大，特别是当网格量较大时。本文在求解式（19）时，只计算少量网格上的残差以优化参数ξ，这大大减少了降阶模型求解的计算量，使得流场求解的整个过程中，降阶模型的计算量不到CFD 求解的1/10，这是本文方法能够有效的一个关键点。

加速收敛方法包含的步骤：①基于流场初值U0m进行短时间内的CFD 迭代，保存求解过程中Um、Ump、∇Ump、ULmp、URmp的快照；②从快照中提取能量最高的POD 模态，并使用Galerkin 投影将数值格式投影到POD 模态上得到降阶模型式（19）③使用梯度优化最小化降阶模型平均残差R(ξ)，从而得到残差更低的流场，更新U0m；④重复步骤①～步骤③，直至收敛。

本方法中主要超参数有：计算降阶模型平均残差R(ξ)时使用的网格数M 和网格的采样方式、流场快照数目N、快照保存间隔K。

2 典型算例验证

本节将采用多个典型流场算例验证所提加速收敛方法在复杂流动求解中的有效性以及参数敏感性。分别为NACA0012 翼型绕流的无黏算例和湍流算例、S809 翼型绕流湍流算例以及ONERA M6 机翼的亚声速湍流算例。算例均采用二阶有限体积法，无黏通量采用Roe 格式计算，黏性通量采用中心格式计算，时间推进方法为隐式Gauss-Seidel 迭代。

2.1 NACA0012 翼型绕流无黏算例

NACA0012 翼型无黏算例中，来流马赫数Ma=0.3，攻角α=0°，CFL=5，网格总数16 155，近壁面网格如图1 所示。每隔200 步进行一次降阶模型求解，快照数目N=40，保存间隔K=5。分别随机选取200、500、1 000、2 000 个网格点计算降阶模型的平均残差，以测试网格点数对加速方法的影响。计算得到的流场残值收敛历程如图2 所示，不同方法所用的时间统计如表1所示。

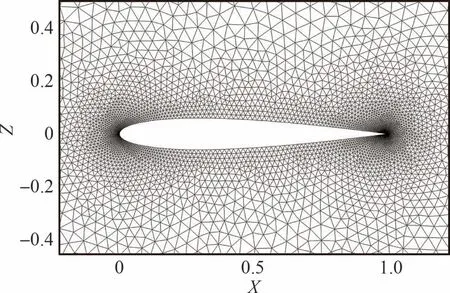
图1 NACA0012 翼型无黏网格Fig.1 Inviscid grid of NACA0012 airfoil

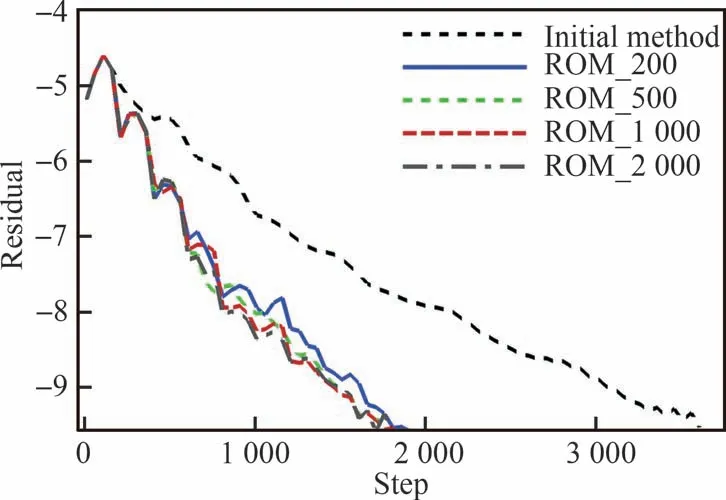
图2 不同网格点数的加速方法收敛历程Fig.2 Residual history with different numbers of grids

表1 不同网格点数的加速方法计算时间Table 1 Calculation time with different numbers of grids

由图2 和表1 可知，所提的加速收敛方法对于无黏流动能达到约1.5 倍的加速收敛效果，从收敛历程来看，该方法对于网格数的选取不敏感，但由于降阶模型中计算的网格数越多，降阶模型计算时间越长，因此网格数M不宜太大。图3 给出了加速方法和初始CFD 方法的压力系数Cp分布对比，可看出2 种方法计算得到的翼型表面压力分布一致。事实上，因为降阶模型中的快照来源于CFD 计算并且被不断更新，所以加速收敛方法的精度仍然取决于CFD 计算过程，不会损失任何精度。

图3 翼型表面压力分布对比Fig.3 Comparison of surface pressure coefficient

2.2 NACA0012 翼型绕流湍流算例

本节计算NACA0012 翼型的湍流算例用于测试加速收敛方法在复杂工程湍流问题中的有效性。来流马赫数Ma=0.3，攻角α=8°，雷诺数Re=3×10-6，CFL=2，网格总数为76 356，近壁面网格如图4 所示。

图4 NACA0012 翼型黏性网格Fig.4 Viscous grid of NACA0012 airfoil

该算例中，每隔200 步进行一次降阶模型求解，快照数目N=20，保存间隔K=10。求解降阶模型时，只计算1 000 个网格点上的残值。给出了3 种不同的采样方式确定这1 000 个网格点，分别是：①随机采样；②选取残差最大的网格点；③选取流场特征相差最大的一组网格点（通过计算不同网格流场值之间的相关性确定）。得到的流场残值和阻力系数CD收敛历程如图5 所示。

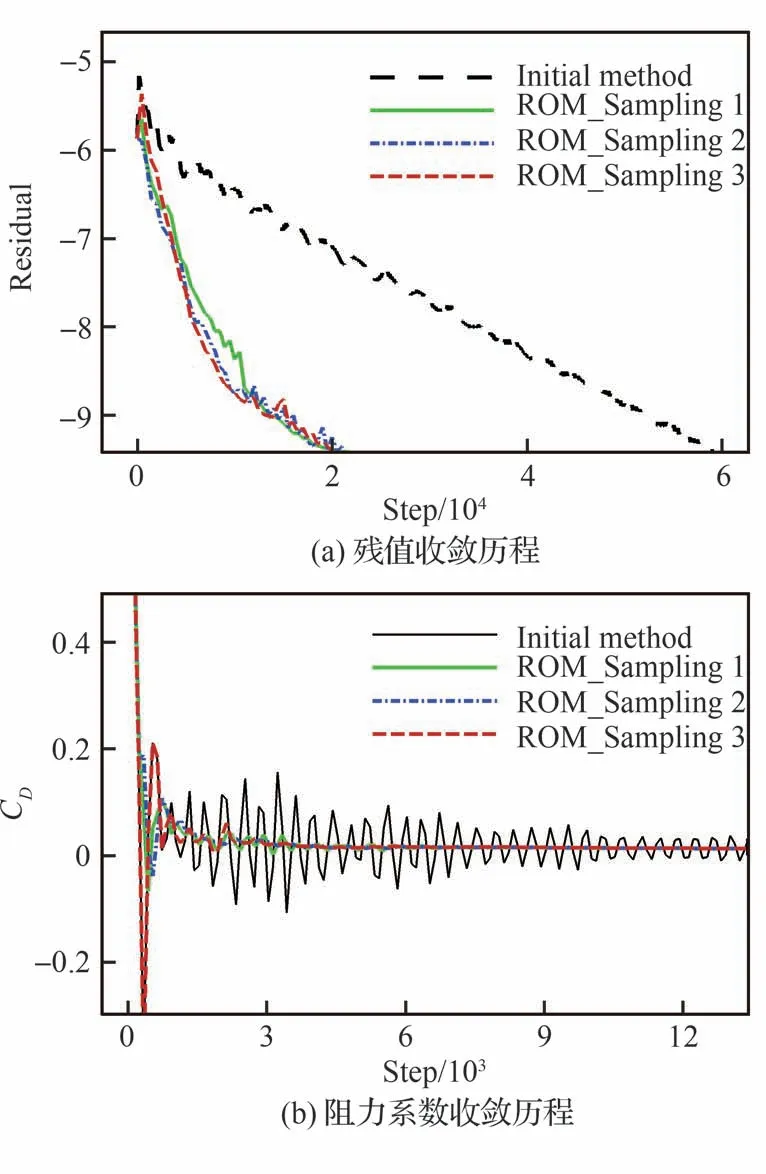
图5 不同采样方式的加速方法收敛历程Fig.5 Residual history with different sampling methods

图5 和表2 表明，加速收敛方法对降阶模型中网格点的采样方式不敏感，不同的采样方式均能达到约3 倍的加速效果，但采样方式2 和3 均会带来额外的计算量，因此在本文的其他算例中，均只采用随机采样网格的方法。另外，加速方法和初始的CFD 方法相比压力分布和摩擦阻力系数Cf分布也基本完全一致，结果如图6 所示。

图6 NACA0012翼型表面压力分布和摩擦阻力分布对比Fig.6 Comparison of surface pressure coefficient and skin friction coefficient （NACA0012）

表2 不同采样方式的加速方法计算时间Table 2 Calculation time with different sampling methods

2.3 S809 翼型绕流湍流算例

本节采用S809 翼型湍流算例用于测试加速收敛方法在流场中存在大分离时的加速效果，来流 马 赫 数Ma= 0.2，攻 角α= 14.2°，雷 诺 数Re= 2 × 10-6，CFL = 5。网格总数为34 205，近壁面网格如图7 所示。

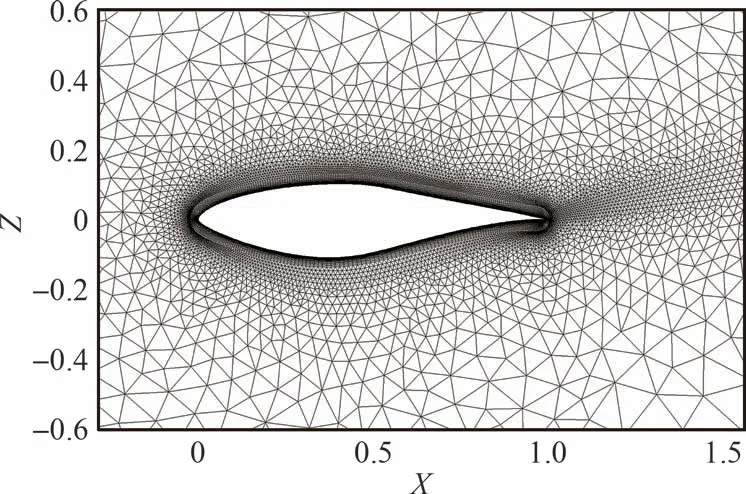
图7 S809 翼型黏性网格Fig.7 Viscous grid of S809 airfoil

该算例中测试了4 种不同快照参数（快照数目N和保存间隔K）对加速效果的影响，得到的流场残值收敛历程如图8 所示。

图8 不同快照参数的收敛历程Fig.8 Residual history with different snapshot parameters

由图8 和表3 可知，对于流场中存在大分离的湍流问题，加速收敛方法仍然有效，且加速收敛方法对降阶模型中快照数目和保存间隔不敏感，不同的参数均能达到约3 倍的加速效果。另外，加速方法和初始CFD 方法相比压力分布和摩擦阻力分布也完全一致（图9）。同时，2 种方法计算得到的压力云图和分离区也一致（图10）。

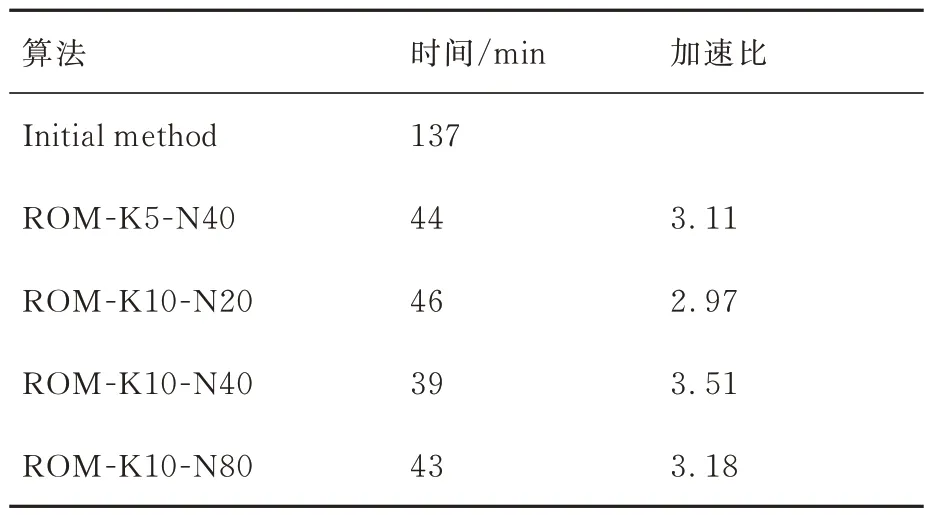
表3 不同快照参数的加速方法计算时间Table 3 Calculation time with different snapshot parameters

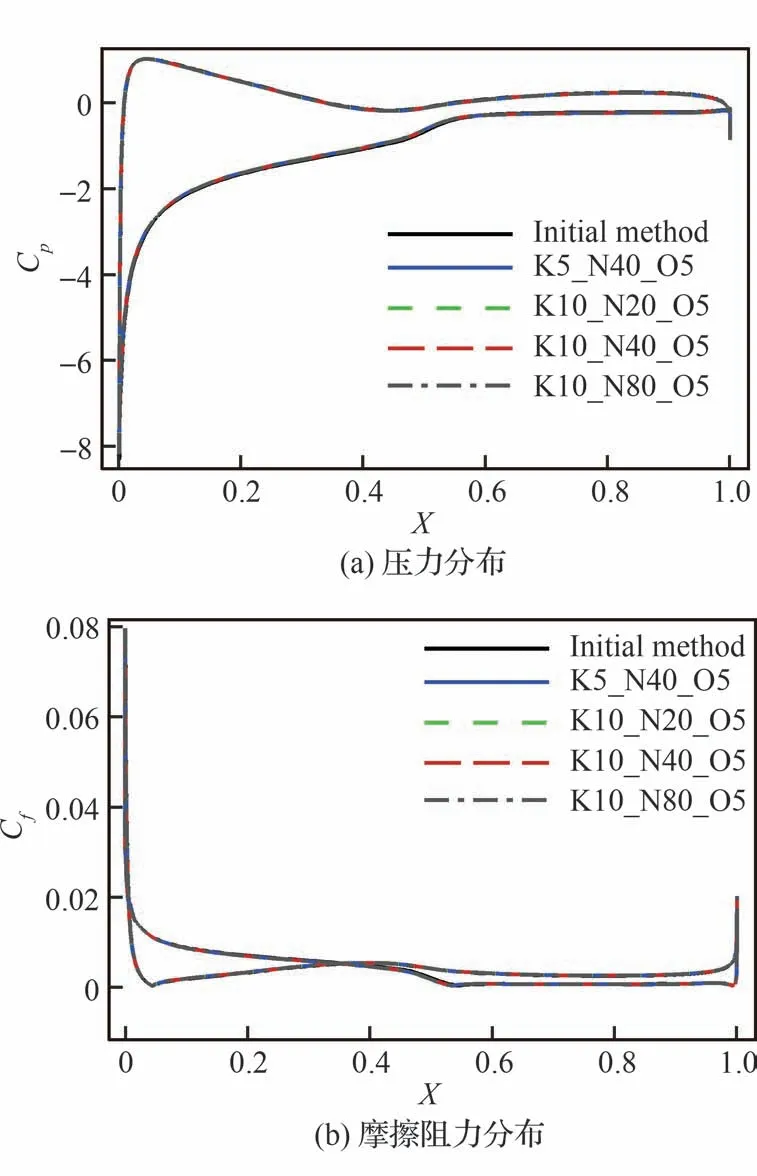
图9 S809 翼型表面压力分布和摩擦阻力分布对比Fig.9 Comparison of surface pressure coefficient and skin friction coefficient （S809）

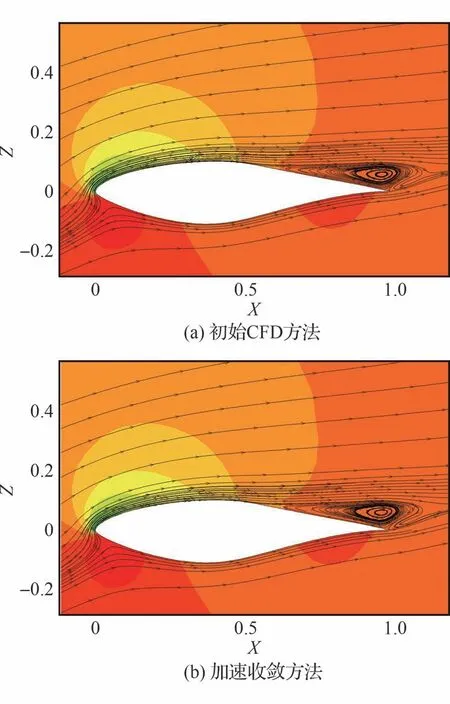
图10 压力云图对比Fig.10 Comparison of pressure contours

2.4 ONERA M6 机翼绕流湍流算例

本节将加速收敛应用于三维ONERA M6 机翼亚声速绕流问题，验证该方法对于三维问题的有效性。ONERA M6 机翼网格如图11 所示，网格总数30 万，来流马赫数Ma=0.3，攻角α=8°，雷诺数Re=1.172×10-7，CFL=1。该算例中网格数M取5 000，流场快照数目N=20，快照保存间隔K=20。

图11 ONERA M6 机翼网格Fig.11 Grid of ONERA M6 wing

图12 和表4 分别为该算例的收敛历程和总用时，它们表明，对于复杂三维问题，加速收敛方法仍然有效，能够实现残值的快速下降。从气动力系数收敛曲线也可以看到加速收敛方法波动更小。图13 给出了20%展长处机翼截面的压力分布，可以看到2 种方法具有相同的收敛精度。

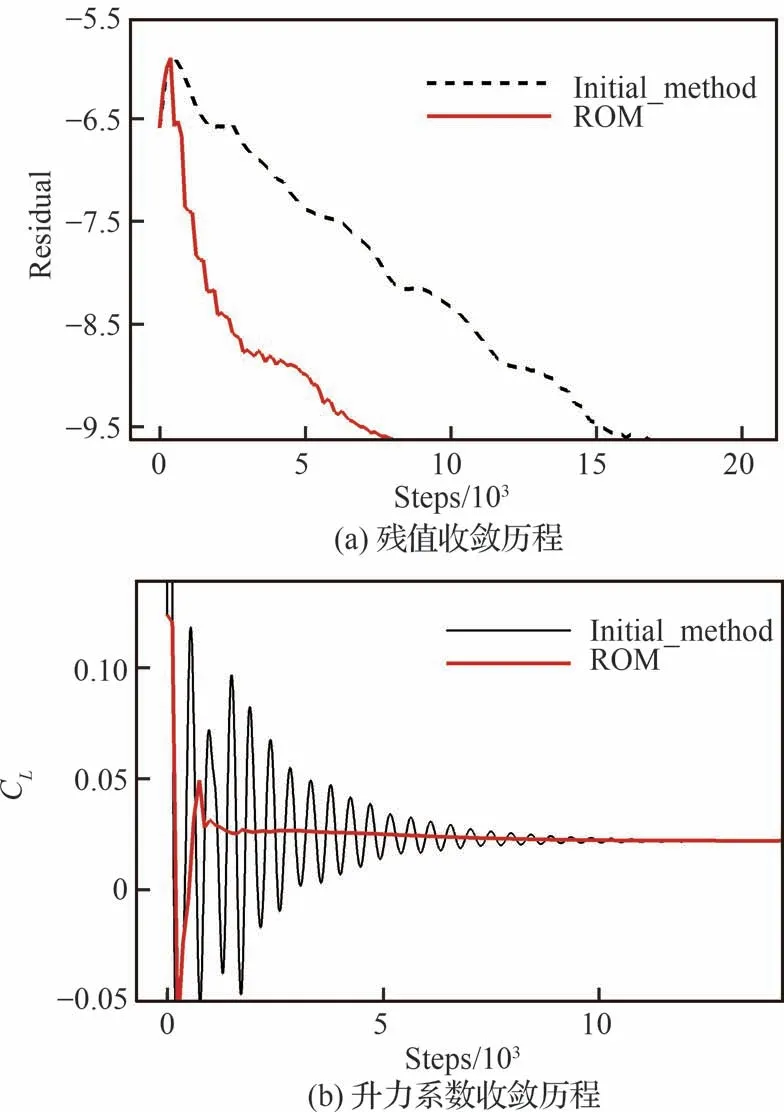
图12 收敛历程（ONERA M6 机翼）Fig.12 Residual history （ONERA M6 wing）

表4 不同方法的计算时间Table 4 Calculation time of different methods

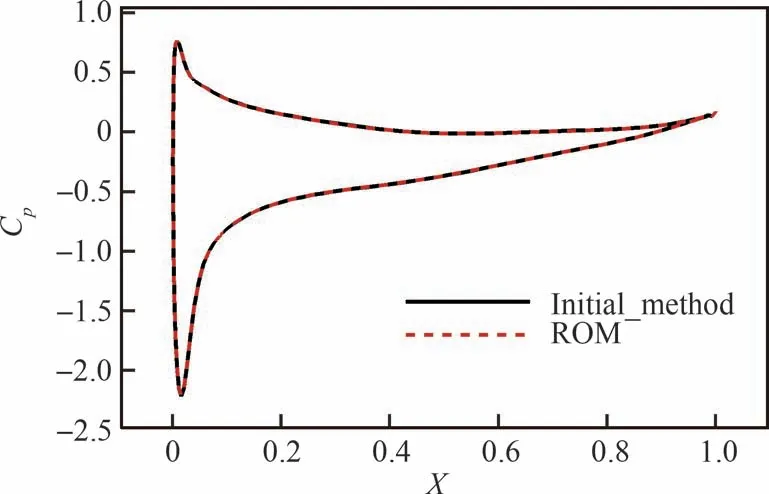
图13 20%展长处机翼截面压力分布对比Fig.13 Comparison of pressure coefficient of 20% wing cross-section

3 结 论

本文提出了一种基于降阶模型和梯度优化的加速收敛方法。该方法收集CFD 计算过程的流场快照，从快照中提取能量最高的POD 模态而后构建基于POD 模态降阶模型。通过CFD 迭代和降阶模型的交替求解实现加速收敛。特别地，本文采用梯度优化最小化降阶模型的残差，相比于其他迭代方法更灵活，且不存在稳定性问题。在该方法的框架下，降阶模型中只是关于流场快照的简单代数运算，并不涉及不同网格之间的相互运算。因此，降阶模型部分很容易在额外模块中实现，不需要对CFD 求解器源代码进行改动，只需让CFD 求解器在合适位置保存流场快照即可，大大降低了嵌入式降阶模型实现难度。

本文中的算例表明，所提出的加速收敛方法是鲁棒的和高效的，对于无黏、湍流流动均有明显的加速效果，是一种颇具潜力的加速收敛方法。在进一步的工作中，该方法可考虑应用于非定常流场的加速求解，使用降阶模型预测双时间步中内迭代的初值以加速内迭代步收敛。同时，该方法在较大规模网格的流场求解中也有潜在价值，也将在未来的工作中进行测试和研究。