数学概念形成过程中基于“起点”的问题提出设计*

李太敏 (江苏省灌南县教师发展中心 222500)

江宋标 (江苏省灌南县六塘中学 222500)

数学概念是构成数学内容的最基本的单元,是学生进行数学思维的细胞．概念教学在数学课堂各类教学中具有举足轻重的地位,而在数学概念教学中具有重要地位的则是“问题提出”,正如美国教育哲学家布鲁巴克所说的,“最精湛的教学艺术,遵循的最高准则就是让学生自己提出问题”．要让学生能提出问题,关键是教师要善于设计问题提出的起点,这些设计起点所反映出来的观念要能够让学生提升对数学教育教学的看法,学会用数学的方式对事物进行观察、思考、表达,感悟寻求运动变化中相互联系与规律的思想价值,体现分析与解决问题能力的智力价值,能对数学概念的定义方式、怎么样研究概念具有方法论的意义．本文试以江苏省优质课评比中的课例“弧度制”为例来对此说明．

1 基于学生的认知起点提出问题:让学生学会循序渐进地发现规律

学生的认知起点指的是学生在学习某个新的知识点之前已经有的与之相关的生活、知识经验基础．虽然这些基础会因为学生的特殊差别而不同,但学生在学习同一个知识点时一定会有许多共同的优势与短板,体现在学生的认知发展过程中,对客观世界的认知呈现出循序发展的规律,总是随着有效智力劳动的增加而实现循序渐进(含螺旋式上升),这也为寻找学生的学习起点提供了依据．认知心理学家奥苏贝尔曾说过:“假如让我把全部教育心理学仅仅归纳为一句话,那么,我将一言以蔽之:影响学习的唯一重要因素,就是学习者已经知道了什么,要探明这一点,并应据此进行教学．”因此在数学教学设计中应认清学生的认知起点,尽力做到在引进新概念时有的放矢,尽可能地让学生感觉到这些新概念的引进是很自然的,甚至是不可避免的．

案例1“弧度制”概念形成过程设计．(2019年江苏省优质课比赛示范课研讨课例,江苏省扬中高级中学宫建红执教)

师(提出问题1,目的是引出并回顾角度制的概念):怎样度量一个角的大小?

生:用量角器或借助量三角形的边长等．

师:从三角学的发展历史看,三角学是依托圆而存在的,因此我们可以看到角度制的定义依托于圆周,采用等分的思想先定义度量的单位:1度的角,再进行度量一般的角．尽管“角度制”的定义依托圆周,但一定大小的角与圆周的大小(即半径大小)是无关的．

师(提出问题2,目的是引出圆心角所对弧长与半径的比值随角的确定而唯一确定):角的大小与什么有关?请看圆心角为30°时,试着求出当半径分别为1,2,3,4时所对弧的弧长．它们有什么共同的特征?

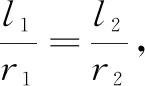
师(总结):不论是从特殊到一般,无论用代数方法还是几何方法,都能得出共同的结论,即对同一个角来说,弧长比半径不变(定值)!那么对不同的角呢?

生:对不同的角来说,这个比值不一样!

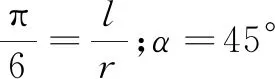
师(提出问题3,目的是引导学生建立新的单位):可以用此方法度量一般的角的大小吗?如何建立一种新的度量角的制度?

生:首先要定义“单位”!

师:你会如何定义1单位的角呢?有了度量的单位,你能度量其他角吗?

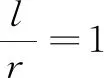
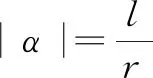
设计分析弧度属于几何度量问题．高中生在学习弧度之前,已学过长度、角度、面积、体积的度量,这些几何量的共性是都有大小,它们的大小可以通过比较来确定.在比较过程中需确定单位,它们的差异是所用的单位不同:长度单位是人为规定的,在此基础上定义的面积、体积也是如此;角度单位是自然规定的,把圆周分成360份,其中一份所对的圆心角作为角的度量单位,即度.因此,弧度制的教学可从学生的认知出发纳入几何度量问题中,通过与长度、角度等度量的类比,体现新的度量制度确定单位的自然与必要[1]．为了体会这样选择单位的一般性,需要说明在圆心角确定时,它所对的弧长与半径的比是定值,并且不论是以“弧度”还是以“度”为单位的角的大小都是一个与半径大小无关的定值．弧度制是十进制的,每个角都有唯一的实数与它对应,同时每个实数也都有唯一的一个角与它对应,这也为学习任意角的三角函数奠定了坚实的基础．

2 基于逻辑起点提出问题:让学生学会理性地发现、分析问题

数学的存在、发生与发展经历了漫长的过程,而这种发展常常是基于某种现实需要或数学内部发展的需求.例如数学概念的发展,有的是基于具体的现实模型或数学原型;有的是基于对某种规律的浓缩;有的是基于构建数学理论的需要而合理扩充,甚至虚构;有的是基于逻辑需求推演而来．在数学教学设计中,了解这种需要及数学各部分的作用,了解它们的依赖关系及它们的综合交错作用才能构成数学教学的丰富内涵,这也有助于对数学这个有机整体的认识[2]．其中数学内部发展的需求常常是基于逻辑需求,因此从逻辑起点出发,能够让学生学会有逻辑地思考问题,能够在比较复杂的情境中把握事物之间的关联,把握事物发展的脉络,形成重论据、有条理、合乎逻辑的思维品质和理性精神,增强交流能力．

案例2“弧度制”概念形成过程设计．(2019年江苏省优质课一等奖获得者课例,启东中学胡勇执教)

师(导语):同学们,很高兴能来到江苏省常州中学参加这次优课比赛,很巧昨天正好是我儿子10周岁的生日,我买了个蛋糕,经过中心将圆形蛋糕切三刀分成了6块,这6块大小相差无几．欲从中挑出最大的一块给儿子,同学们帮我想想办法．

生:用量角器度量、比较弦长或弧长．

师(提出问题1,以寻求逻辑关系式):当弧长l一定时,随着半径r的增大,圆心角α发生什么变化?弧长l、半径r和圆心角α三者之间存在怎样的数量关系式?

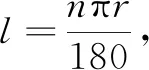
师(提出问题2,以构建逻辑链):圆心角随着l与r的比值的确定而唯一确定,从而可利用l与r的比值来度量圆心角．而认识一种新的单位制,首先得明确它的单位1,只有明确单位1后,才可以定量表示其余的量．如何确定单位1呢?

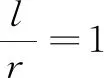
师(概念形成):长度等于半径长的弧所对的圆心角叫作1弧度的角,记作1 rad.用弧度作为角的单位来度量角的单位制叫弧度制．

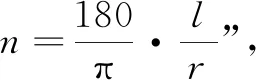
3 基于历史的形成过程的起点提出问题:让学生学会从历史溯源中求真、求变

数学概念的产生过程常包含逻辑过程、现实形成过程、历史过程等,它们并非等价,同一数学概念的发展与逻辑过程并非同步,不同概念的发生也不是完全根据逻辑过程来的,在历史上常常有意外．例如,从逻辑上讲,应先有指数后有对数,但历史上恰恰相反．而编写教材内容时概念的产生一般采用的是逻辑过程,作为数学课堂中的概念教学,有些教师也千篇一律地严格按照逻辑顺序来设置问题,过分强调其逻辑过程,将概念产生的过程一味逻辑化,这有时会影响对概念的本质的发现[4]．在数学教学设计中,虽然无法并且也不必要让“历史重演一遍”,但适当选择性地还原,甚至部分再现数学概念的历史形成过程,从历史起点出发,基于历史的形成过程的起点而提出问题,让学生学会从历史溯源中求真、求变,有时也会起到意想不到的效果．

案例3“弧度制”概念形成过程设计．(2019年江苏省优质课一等奖获得者课例,无锡高级中学刘烨烨执教)

师(提出问题1,目的是回顾度量长度的几种单位而引出怎样规定角的度量单位):当规定好1米有多长,我们可以用米作为单位来度量长度,当规定好1尺有多长,我们可以用尺作为单位来度量长度,1米=3尺;当规定好1度角有多大,我们可以用度作为单位来度量角的大小．那么1度的角是怎么规定的?

生:一个周角的360分之一．

师:能用平分圆周的方法得到1度的角吗?

生:将圆周分为360等份,周角的360分之一弧对应的圆心角就是一度．

师:现在我们要建立新的单位来度量角,那先要对什么做出规定?

生:单位角的大小．

师(提出问题2,目的是将线段与弧的度量统一起来):如果以半径长为单位对圆周进行度量,把长度等于半径的圆弧所对的圆心角定义为一个单位角的大小,合理吗?

生:要探究角的大小不会随着半径的改变而改变．

师(形成概念):把长度等于半径长的圆弧所对的圆心角叫作1弧度的角,记作1 rad．用弧度作为角的单位来度量角的单位制称为弧度制．

设计分析上述设计通过从经历单位长度的定义过程出发,让学生感受历史上弧度制的形成过程:从长度单位到渗透“单位”的思想,从平分圆周定义1度角的大小的角度制到利用平分圆周的思想定义一个新的单位角,体会1弧度角定义的合理性来源,同时意识到规定单位角的大小是定义新的度量单位的前提．这样设计以历史起点作为教学起点,以寻找新的度量单位为目标,发现了用长度来度量角,弧度制与角度制一样都采用了“等分”思想:弧度制可以理解为是用长度来度量角的一种单位,可以理解为是对圆周不同的平分方式,即规定弧长等于半径长的弧所对的角为1弧度．正如欧拉在其著作《无穷小分析概论》中提出把圆的半径作为弧长的度量单位,这一思想将线段与弧的度量统一起来,大大简化了三角的运算．而这也是弧度制的本质:用半径对圆周进行度量.这样的度量统一了三角函数自变量和函数值的单位,能进行基本初等函数运算．

当然,需要说明的是,在数学概念形成过程的教学中,无论是基于学生的认知起点提出问题,还是基于逻辑起点提出问题,以及基于历史的形成过程的起点而提出问题,这些方法的设计并不相互冲突,也并非一定独立使用的,事实上它们常常是并存或交叉的,也就是说可以同时合用其中的两种甚至三种设计方法．