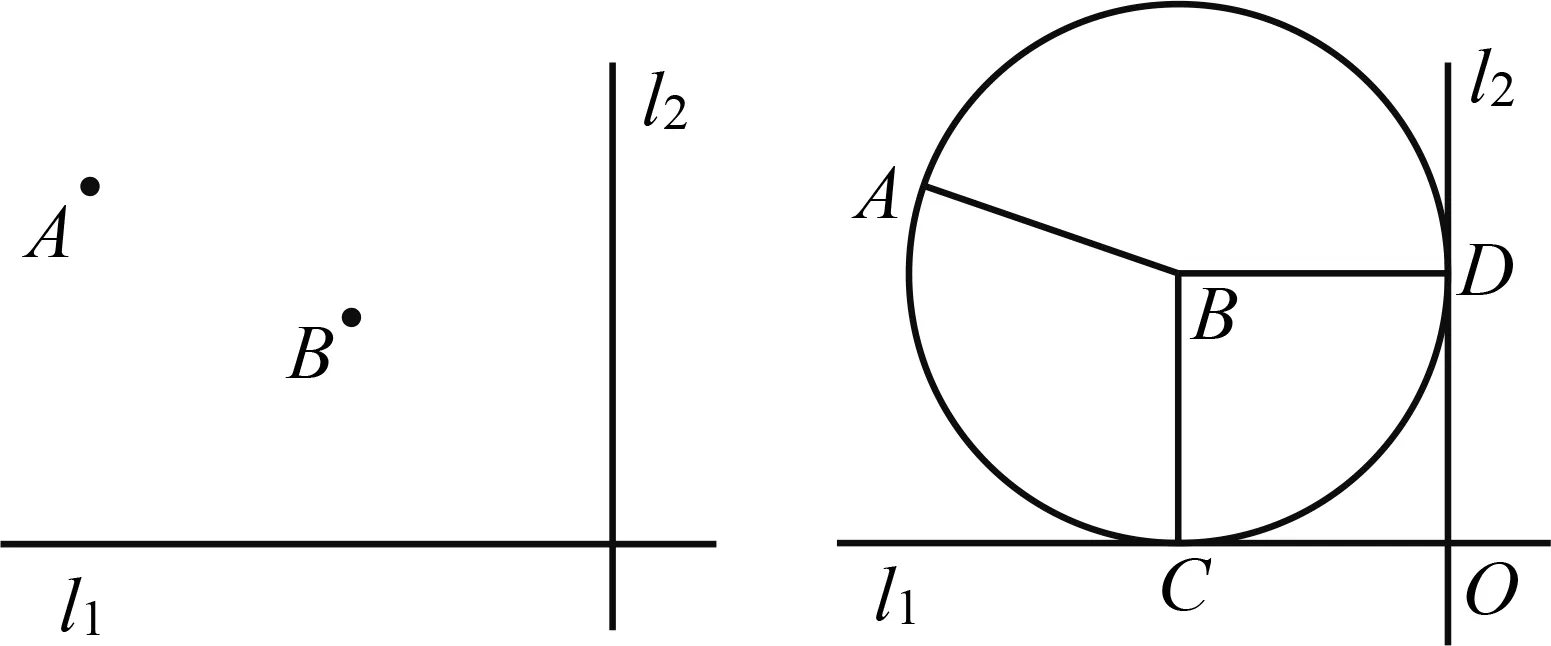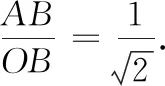加强尺规作图教学 发展几何直观素养*
2023-04-17丁银杰江苏省苏州市草桥中学校215031
丁银杰 (江苏省苏州市草桥中学校 215031)
尺规作图是“图形与几何”领域的课程内容.《义务教育数学课程标准(2022年版)》(以下简称《课标2022版》)强化了尺规作图的教学功能与育人价值,其第四学段的学业要求是:“经历尺规作图的过程,增强动手能力,能想象出通过尺规作图的操作所形成的图形,理解尺规作图的基本原理与方法,发展空间观念和空间想象力.”[1]
1 加强基本作图教学,理解尺规作图原理
尺规作图是指用无刻度直尺和圆规进行作图.无刻度直尺不具有度量长度的功能,用来经过两点作线(直线、射线或线段).圆规用来作弧,圆规两脚可以“拾取”线段长度或两点之间的距离.尺规作图关键是确定“线与线”“线与弧”或“弧与弧”的交点,从而构造出符合要求的图形.
以5个基本作图为例,剖析一下尺规作图原理.关于基本作图,教材有详细而规范的作法.作出图形并不难,理解其中的数学原理才是核心.建议在“全等三角形”章后增加1节“基本作图”专题课,在体现全等三角形在数学内部应用的同时,帮助学生系统建构基本作图的认知(作法与原理).
在“作一条线段等于已知线段”中,圆规“拾取”线段长度作为圆弧的半径,依据的是两点之间的距离定义(两点之间线段的长度).“作一个角等于已知角”“作一个角的平分线”“作一条线段的垂直平分线”及“过一点作已知直线的垂线”,依据的是全等三角形的判定,其中用圆规作弧实质是根据“同弧的半径相等”构造“相等线段”.基本作图教学要让学生亲历作图过程,明白作法含义,充分说理论证,理解数学原理.
为帮助学生进一步理解基本作图原理,可以适度设计一些开放探究活动,如下面的探究:
用直尺和圆规作∠AOB的平分线OP,并说明理由.
图1呈现的三种有别于教材的作法,是学生自主探究的成果.教师应因势利导,对各种作法进行比较研究,在感受教材作法简洁的同时,感受它们的共同之处:基于角的轴对称性直觉,构造全等三角形,得出两个相等的角,从而更好地理解基本作图的数学原理.
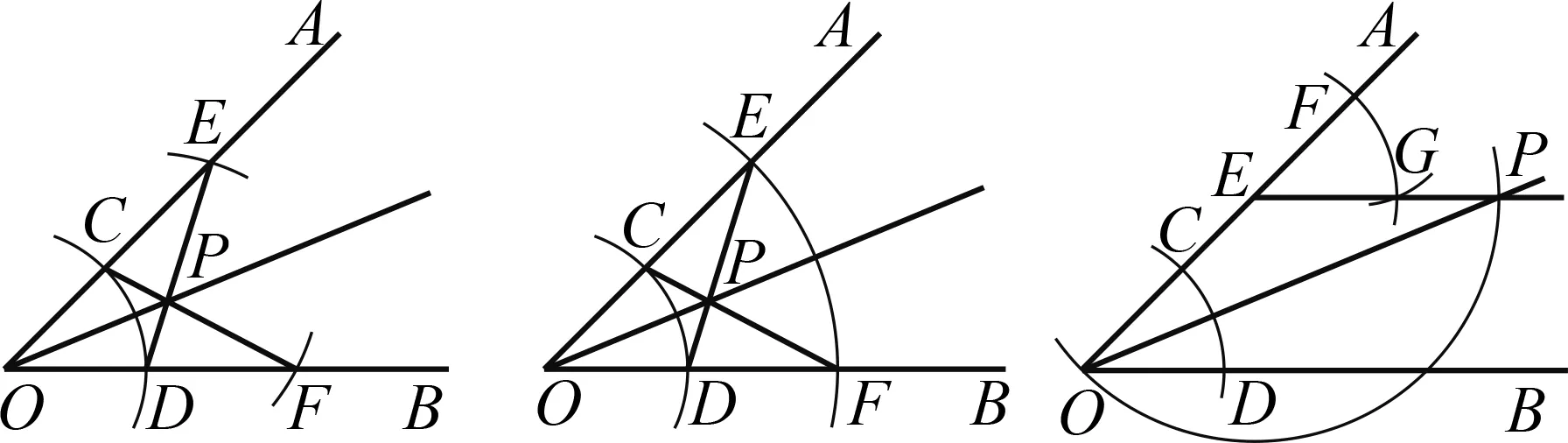
图1
熟练掌握基本作图技能,深刻理解基本作图的原理,是进一步基于尺规作图探究图形性质的重要基础.
2 加强组合作图教学,感受尺规作图价值
基本作图是尺规作图的基础,尺规作图的价值在于应用,实际应用多为基于一定问题情境的组合作图.《课标2022版》关于尺规作图的内容,除5个基本作图(其中“作一条线段等于已知线段”前移至第二学段)外,还包含“过直线外一点作这条直线的平行线”“已知三边、两边及其夹角、两角及其夹边作三角形;已知底边及底边上的高线作等腰三角形;已知一直角边和斜边作直角三角形”“过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和内接正六边形”及“*过圆外一点作圆的切线(注:标有‘*’号的内容为选学内容,不作为考试内容)”等多个基本作图的“组合体”(简称为“组合作图”).
组合作图一般以“操作”或“例题”的形式整合在教材各个章节之中,是基本尺规作图在数学内部的应用,用来帮助学生理解、掌握相应的课程内容.如“已知两边及其夹角作三角形”是探索三角形全等的条件——边角边,获得“基本事实:两边及其夹角分别相等的两个三角形全等”认知的重要载体.苏科版《义务教育教科书·数学》(八年级上册)关于该尺规作图内容设计如下:
按下列作法,用直尺和圆规作△ABC,使∠A=α,AB=a,AC=b.
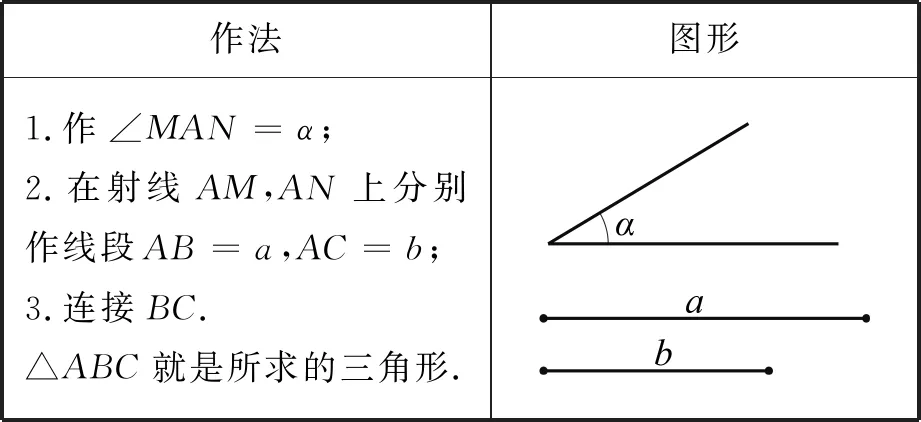
作法图形1.作∠MAN=α;2.在射线AM,AN上分别作线段AB=a,AC=b;3.连接BC.△ABC就是所求的三角形.
组合作图“已知两边及其夹角作三角形”是“作一个角等于已知角”与“作一条线段等于已知线段”两种基本作图的组合,作法以基本作图为单位“模块化”呈现,简洁明了.实际教学中,可以将其设计成适度开放的问题,以便暴露学生真实思维.进一步可以对其进行变式探究,设计如下问题:
用直尺和圆规作△ABC,使∠A=α,AB=a,BC=b.
通过个人自主作图,小组合作交流,不难在组合作图实践的基础上获得“两边及其一边的对角不能唯一确定三角形”(图2)的结论,即“边边角”不能作为三角形全等的判定方法,积累用“举反例”说明问题不成立的基本经验.
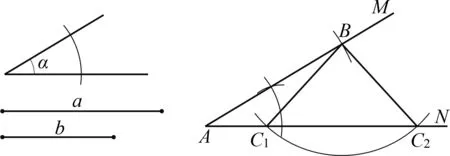
图2
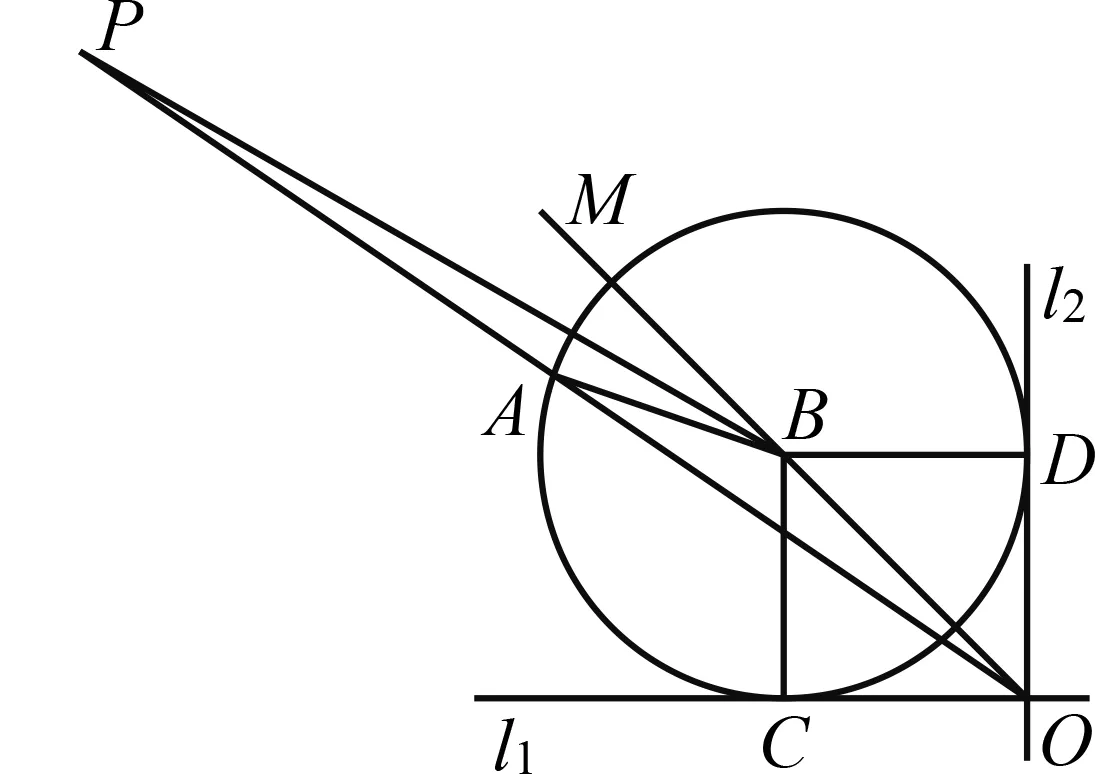
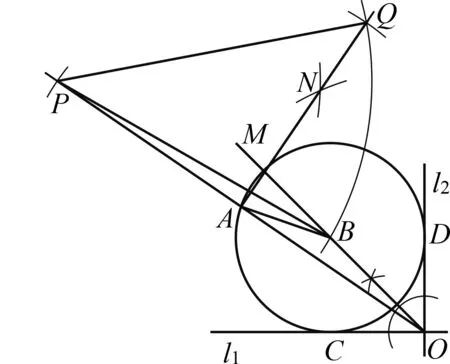
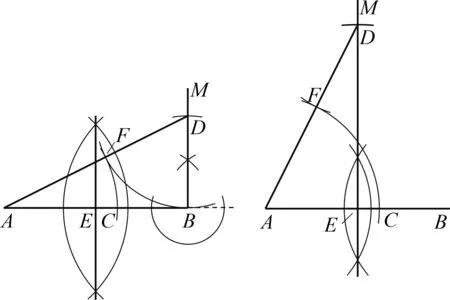
继续通过作图探究,可以得到当α、线段a不变时,△ABC的存在性及个数由线段b决定.如 图3,设点B到射线AN的距离为d,当b 图3 组合作图集中体现了基本作图在图形认识中的重要价值;组合作图教学有助于学生初步形成基于作图的探究能力,发展空间观念与直观想象能力. 除根据作法作图外,尺规作图问题一般都 具有开放性,其一般思路为:构思图形—设计流程—作图验证.构思图形就是借助于想象,勾勒出草图,用分析法执果索因,厘清图中各元素之间需要满足的数量和位置关系;设计流程就是根据构思图形中各元素满足的数量和位置关系,运用综合法,调用相关数学知识由因导果,确定作图的基本步骤;作图验证就是将设计流程中的基本步骤具体化,分解成基本作图串,依次作出相应图形,并加以验证.当然这一过程不一定一帆风顺,可能需要经历多次调整,甚至推倒重来.即便是成功的思路,也有可以优化的地方.以用尺规作图作线段的黄金分割点为例: 已知:线段AB(图4). 图4 图5 求作:线段AB的黄金分割点C,且AC>BC. 作图验证:如图6,(1)作线段AB的垂直平分线,交AB于点E;(2)过点B作线段AB的垂线BM,在射线BM上作线段BD=BE;(3)连接AD,在线段AD上作线段DF=BD;(4)在线段AB上作线段AC=AF. 图6 图7 点C即为线段AB的黄金分割点. 证明略. 反思一下作图过程,不难发现,充分运用线段AB的垂直平分线功能,可以对上述作图方案进行优化重组.作法如下: 如图7,(1)作线段AB的垂直平分线ME,交AB于点E;(2)在射线EM上作线段DE=AB;(3)连接AD,在线段AD上作线段DF=AE; (4)在线段AB上作线段AC=AF. 点C即为线段AB的黄金分割点. 证明略. 开放作图侧重策略开放,围绕既定目标图形,由结论回溯条件,设计各种可行方案,并进行优化迭代.开放作图有利于培养学生基于图形直观的理性思维,发展分析和解决问题的能力. 数学来源于对生活的抽象,又通过模型作用于生活,有着广泛的应用性.基于生活情境,通过抽象将现实问题数学化,基于数学分析,用尺规作图构建几何模型,运用模型思想分析、解决问题,是尺规作图应用教学的基本路径.加强基于真实情境的应用作图教学,可以有效发展学生的几何直观素养,培育学生的应用意识与创新意识.以下面的问题为例: 如图8,l1,l2为两条互相垂直的公路,点A为工厂,现拟新建仓库B,用来储存、转运工厂A生产的产品.若要求仓库B到公路l1,l2和工厂A的距离相等,试确定仓库B的位置. 图8 图9 数学化:如图9,设l1,l2交于点O,连接AB,再由点B分别向l1,l2作垂线,垂足分别为C,D,则由仓库B到公路l1,l2和工厂A的距离相等,可得AB=BC=BD,即A,C,D三点都在⊙B上.故问题转化为如何确定与直线l1,l2都相切且经过点A的圆的圆心B的位置. 图10 具体作法如下: 如图11,(1)作l1,l2夹角的平分线OM;(2)作射线OA,在OA上作线段AP=AO;(3)过点A作AO的垂线AN,在射线AN上作线段AQ=AO;(4)连接PQ,以点P为圆心、PQ长为半径作弧,交射线OM于点B,连接PB,AB. 图11 点B即为所求的点. 会数学化(抽象)、会构造(建模)是创新意识的典型行为表现,体现了数学课程的素养导向和育人价值.基于真实情境提出真实问题,用尺规作图方式进行探究,是提升学生问题解决能力、发展几何直观、培育应用意识和创新意识的重要途径. 加强尺规作图教学研究,引领学生基于尺规作图进行数学探究,是实践贯彻新课标理念的重要举措,可以调动学生的自主学习热情,增强学生动手实践能力,发展学生推理能力和几何直观,培育学生应用意识和创新意识.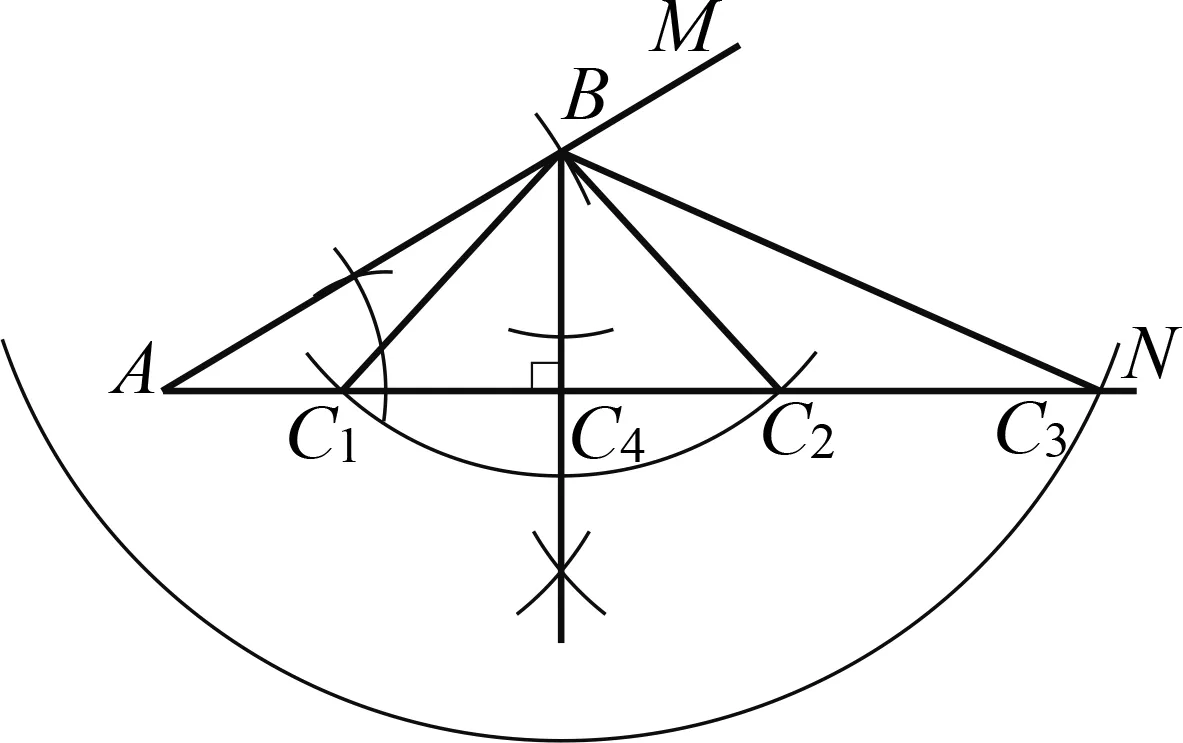
3 加强开放作图教学,明晰作图基本思路
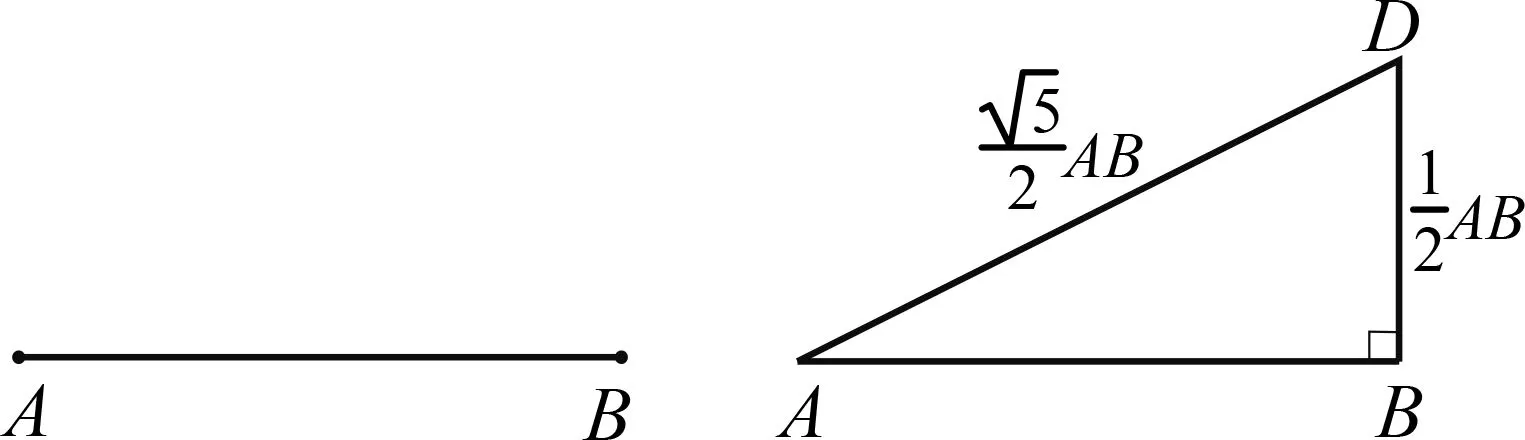
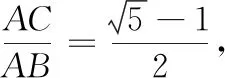
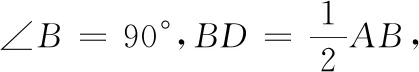
4 加强应用作图教学,培育应用创新意识