“反比例函数”反在哪难在哪
——“反比例函数”认知分析及教学建议*
2023-04-17胡晋宾江苏第二师范学院数学系210013
胡晋宾 (江苏第二师范学院数学系 210013)
刘洪璐 (南京师范大学附属中学 210003)
1 问题提出
在很多人看来,虽然初中和高中都有函数内容,但是相对高中来说初中函数内容比较简单,日常学与教似乎没有多难.在2022年的多次网络讲座中,义务教育数学课程标准修订组组长、东北师大史宁中教授和北京师大曹一鸣教授却都说反比例和反比例函数较难,并在修订课标时把原来放在小学的反比例内容挪到初中去.反比例(函数)相关内容的日常教学实践中,确实存在这样的现象:虽然很多学生知道定义,也能熟练解题了,但是顾名思不了义,并不明白反比例(函数)到底“反”在哪里;一线教师对难学难教的症结在哪里也存在一些认识不足.那么,教学中应该怎样去破解相关难点,以便更好地落实当下核心素养课改理念呢?
2 认知分析
2.1 反向问题的复杂性
第一,正反问题大量存在.在数学、物理甚至社会生活中,因为事物是普遍联系和相互作用的,所以正反问题是普遍存在的.以数学为例就有:正数与负数、加与减、乘与除、指数与对数、三角和反三角、映射与反演、函数与反函数、正反比例与正反比例函数(实质是乘除差异)、直接证法与间接证法(反证法)、原命题和逆命题……能否从正反两个方面思考问题,可以体现思维品质的高低.
第二,反向问题教学较难.反向问题是相对于原来问题提出的,一般有关反向的问题,在认知上都相对较难.比如:多项式乘法简单,但是分解因式很难;求导不难理解,但是积分很难;正数理解起来相对简单,但是历史上西方人对负数的认识和接受就相当费劲,纷纷认为这是不合理的数,等等.又如,以反证法为例,在证明过程中,需要进行反设,经过严谨的演绎推理后得出矛盾,追究原因后得出根源在于反设的谬误性,从而反过去得出命题的正确性.从思维上来看,它有数个逻辑转折,采用了矛盾律和排中律等规律,因此对人的认知要求偏高.反向问题的学习就好比驾考中最难掌握的倒车技能学习一样,因为倒车和正向行驶不一致,需要借助后视镜中的影像进行反向判断后面空间位置信息,从而进行转向操控和距离判断.从教学上来说,反向问题教学也是有困难的,比如,有调查指出,高中教师认为反函数在十大难点概念中排名第一[1].因此,课标将反比例内容放到初中是有道理的,把反函数、反三角等淡化处理是可以削枝强干的.
2.2 超越现实的抽象性
第一,人类认知有缺陷性.数学是研究数量关系和空间形式的科学,具有高度抽象、逻辑严谨和应用广泛等特征,研究内容涉及抽象、无限、弯曲、高维等.初中的反比例函数牵涉无限、弯曲和抽象,但是人类天生对抽象、无限、弯曲、高维的东西,相对具象、有限、笔直和低维的东西,认知起来更加困难.例如,以无限和弯曲为例,正是因为相关问题困难,所以人类才发明了被恩格斯誉为“人类精神的伟大胜利”的微积分.又如,人类生命有涯,为了实现对涉及自然数无限命题的证明,发明了数学归纳法,通过奠基和递推两个环节,实现有限步骤对无穷归纳的把握.再如,函数单调性的定义,也是借助变量的任取,实现对无穷的驾驭(定义如下:“设函数y=f(x)的定义域为A,区间I⊆A.如果对于区间I内的任意两个值x1,x2,当x1
第二,模型与现实有落差.生活中的“反”和数学上的“反”不完全相同.日常生活中所说的“反比”,是指两个事物或一个事物的两个方面,一方发生变化,另一方随之起相反的变化.如老年人随着年龄的增长,体力反而逐渐衰弱,这里只要此消彼长即可,没有具体数量关系要求.数学中所说的“反比例”,要求乘积为定值.例如,x+y=8,两个变量是此消彼长的,符合日常语言中的“反比”关系,但不符合数学中的“反比例”关系,而是数学中的一次函数关系.又如,xy=-1是反比例函数,但是不符合日常中所说此消彼长的“反比”关系,而是随着x增大y也增大的单调递增关系.所以学习反比例函数时,很容易先入为主,把反比例关系和日常生活的反比关系画上等号.不仅如此,当下教材相关内容中,因为过于强调生活现实情境,所以都是从现实案例导入学习的.然而乘积为负常数的案例在生活中并不好举,考虑到数学中反比例函数的定义,于是不得不牵强地告诉学生乘积可以为负(数学中的以下案例学生还没学过:两条直线互相垂直时,若斜率存在则乘积为-1).
2.3 内部关系的负荷性
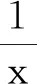
第一,相关概念容易混淆.与反比例函数相关的概念有反比例和反比例关系,很多人认为反比例函数与反比例以及反比例关系不是一回事.实际上,两种相关联的变量x和y在变化过程中,如果它们相对应的每两个数的乘积保持一定(xy=k,k≠0),那么这两个变量就成反比例关系,简称“成反比例”.在数学中反比例、反比例关系与反比例函数是一致的,只是在小学数学中,k的值只限于正数,但是初中教材就不一样了,这是因为数系拓展到了实数.简单说来,反比例(关系)强调的是两种量的关系,而反比例函数是从变量说的角度来看的函数.它们是一样的,在数学里是一个东西,好比穿了不同马甲,在不同场域称谓不同而已.苏步青先生曾经指出,教材编写可以“混而不错”,就是在教材编写中,在充分考虑学生认知水平的基础上,对不必纠缠的次要概念或不易一次说清的非重点内容,可以不犯错误地一带而过,以便提高效率实现循环上升.从这种观点来看,当下没有必要去过度强化反比例、反比例关系和反比例函数的差异(在教参中稍微提一下即可).
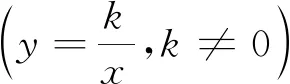
3 策略建议
3.1 强调知识意义建构
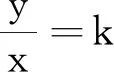
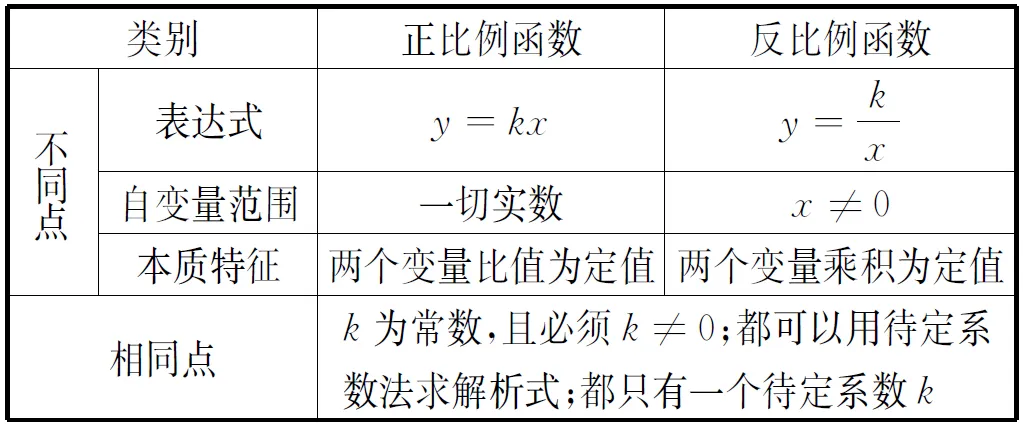
表1 正、反比例函数对比
3.2 注意数学眼光培养
《义务教育数学课程标准(2022年版)》把数学“三会”即会用数学的眼光观察现实世界等,作为数学核心素养的终极目标之一,并指出在义务教育阶段,数学眼光主要表现为抽象能力(包括数感、量感、符号意识)、几何直观、空间观念与创新意识[3].实际上,无论在教材编写中还是课堂教学中,都应该结合生活现实、数学现实以及其他学科现实,将“三会”精神具体拆分为关键能力进行落实.比如在教学中,可以启迪学生思考一个有趣话题:网络热图“葛优躺”的数学解释是什么?实际上,每个人的重量恒定,对于单脚金鸡独立、端坐靠背椅上和四仰八叉地躺在沙发上3种状态,显然它们的受力面积依次增大,因此压强依次减小.这样看来,背后的数学原理就是反比例函数.显然,能够直接看到现实世界中的数学原理,背后体现出的是较好的数学素养,涉及数学抽象、直观想象等综合素质.其他类似的数学眼光案例还有:钓鱼的时候怎样握杆省力气,为什么用针可以扎爆气球,滑雪时为啥要用滑雪板,物理学中的波义尔-马略特定律,等等.当然,我们也需要指出,生活数学、学校数学和真正数学之间存在差异[4].数学源于现实但是高于现实,现实情境也是数学教学的一把双刃剑,处置不当有时候会增加学生认知障碍.教师既要妥善利用好现实情境培养数学抽象、直观想象和应用意识等,也要立足现实世界注意提纲挈领,实现数学发展超越提升.
3.3 狠抓核心素养落实