数学史上的留白与创新

汪晓勤 (华东师范大学教师教育学院 200062)

1 引言

“创新意识”是义务教育数学课程标准提出的数学核心素养之一,如何培养学生的创新意识,是今日数学教育研究的重要课题．美国数学家舒尔茨(A.Schultze,1861—?)在《中学数学的教学》(1939)中已经提到创新的重要性:“数学学习的结果应该是能力的发展,而非事实的获取．一个人知道很多数学事实,并非就是一位好的数学家,只有能够明智地应用这些事实、能够发现全新的事实以及能够重构已经遗忘的事实的人,才是好的数学家．”[1]著名物理学家爱因斯坦(A.Einstein,1879—1955)则强调,学校教育“应当始终将发展独立思考和独立判断的能力放在首位,获得专业知识很次要”[2]．今天,人工智能(如ChatGPT)的应用必将对数学教育产生深远的影响,事实性的数学知识离开课堂也很容易获取,而创新意识和创新能力的培养理应成为数学教学更重要的目标．

在这样的背景下,“留白创造式”教学成了需要人们深入探索的一种教学方式．这种教学方式提倡以学生为中心,通过留白活动,给予学生足够的思维空间和探究机会,让他们经历知识创获的过程,进而达成创新意识和创新能力培养的目标．为了夯实留白创造式教学的理论基础,我们既需要借助数学教育心理学的指导,也需要寻求中国传统教育思想的支撑,还需要从数学历史中寻找思想的启迪．

“留白”一词源于中国古代绘画理论,将该术语用于数学教学,其特定内涵有待于深入探讨．本文拟通过数学史上的若干典型案例的考察,提炼出“留白创造式”教学中的“留白”类型,为未来的相关理论研究和实践探索提供参考．

2 论证之白

我国古代数学名著、成书于东汉的《九章算术》是一部问题集,书中呈现了问题、答案以及解法,但丝毫不提那些解法是如何得来的,也就是说,作者并不交代“所以然”的问题,因而为后世数学家留下了研究空间．

刘徽利用无穷分割求和的方法对公式进行了推导．将长、宽、高分别为a,b,c的长方体(图1)沿对角面剖开,得到两个堑堵(底面为直角三角形的直三棱柱),将一个堑堵沿对角面剖开,得到一个阳马(涂以黑色)和一个鳖臑(涂以红色),如 图2所示．

图1 图2

分别过堑堵底面长、宽和高的中点作平行或垂直于底面的平面,将黑色阳马分割成1个小长方体、2个小堑堵和2个小阳马,将红色鳖臑分割成2个小堑堵和2个小鳖臑,如图3所示．先考虑黑色小立方体、黑色和红色小堑堵(图4),分别将同类小堑堵组合成小长方体,共得到3个小长方体(图5)．这3个小长方体中,黑色和红色部分的体积之比为2∶1．

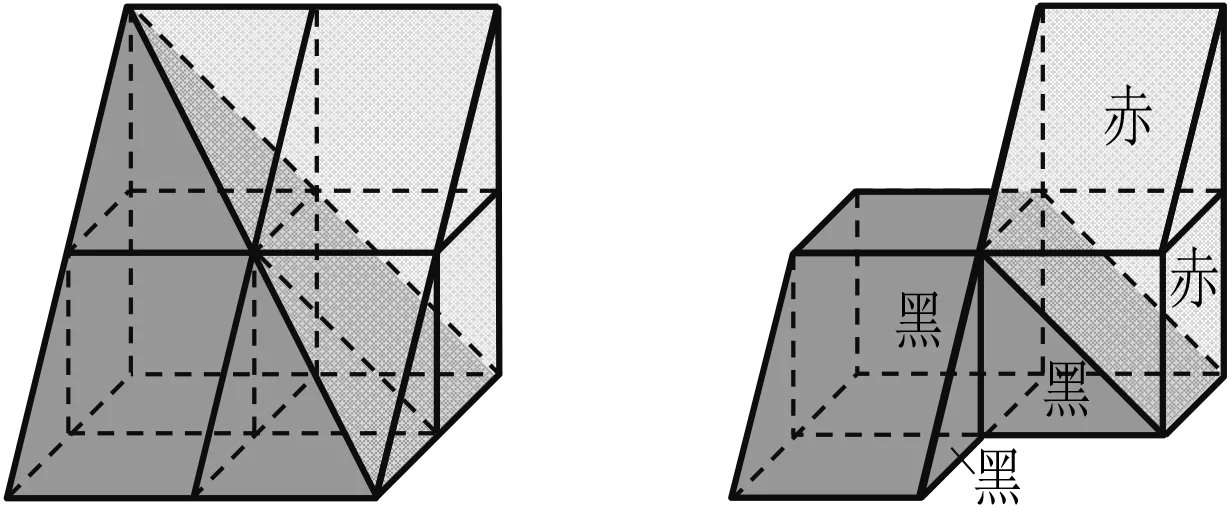
图3 图4

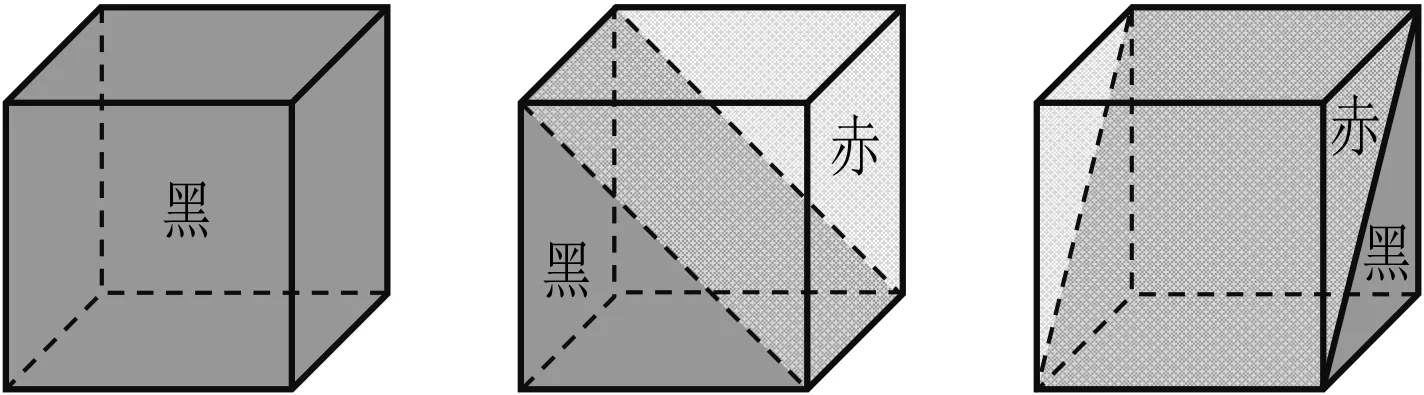
图5

再考虑剩下的2个黑色小阳马和2个红色小鳖臑,共组成2个小堑堵(图6),每个小堑堵的构造与原来的大堑堵完全一样．分别对这两个小堑堵实施同样的分割和重组,所得的6个小长方体中,黑色和红色部分的体积之比为2∶1．

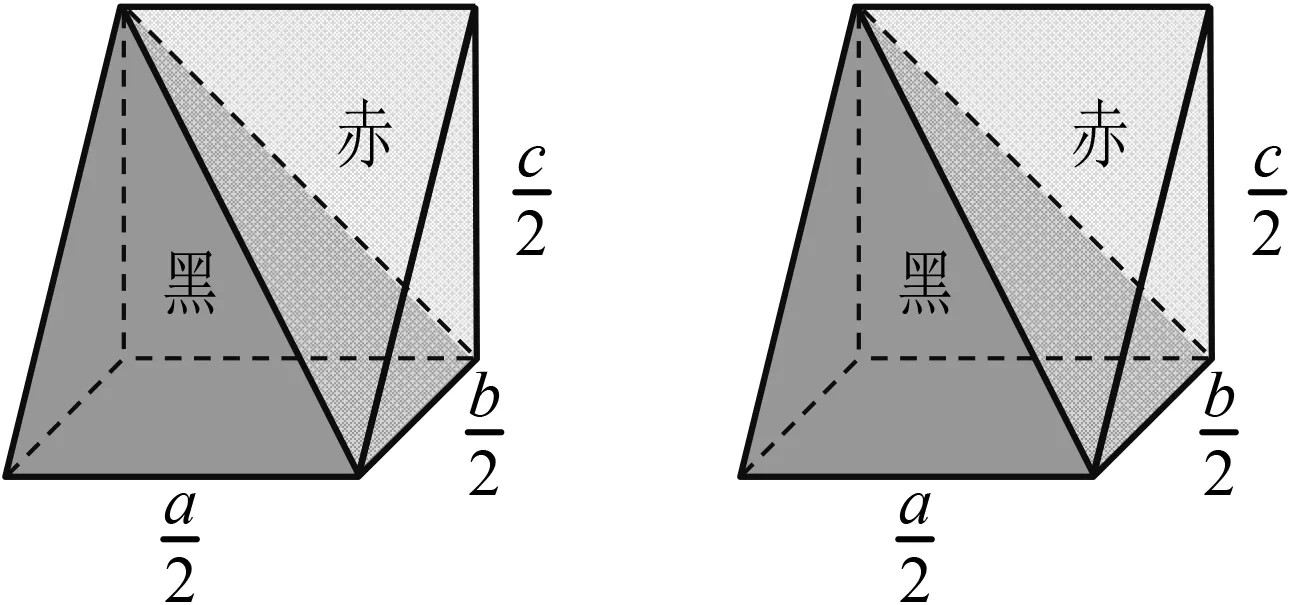
图6

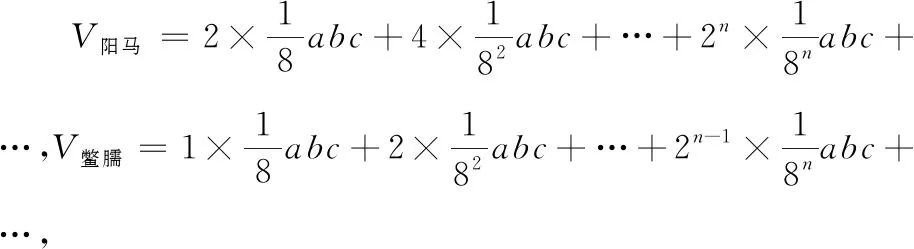
《九章算术》作者的留白,引发了刘徽超越时代的论证．我们将这种为命题的证明、公式的推导等所留出的思维空间称为“论证之白”．

3 发现之白

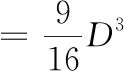
这就表明,汉代数学家的球体积公式是不正确的,利用该公式所得结果大于球体积的真实值,即使是取圆周率为3,结果仍然偏大．

牟合方盖为球体积问题的解决开辟了道路,但是,牟合方盖的体积太难算了．刘徽的思路是:先算出立方体内牟合方盖之外的“碎片”的体积,从立方体体积中减去这些“碎片”的体积,即得牟合方盖的体积．考虑立方体的八分之一部分,其中含有牟合方盖的八分之一部分以及另外三块碎片,如图8所示．

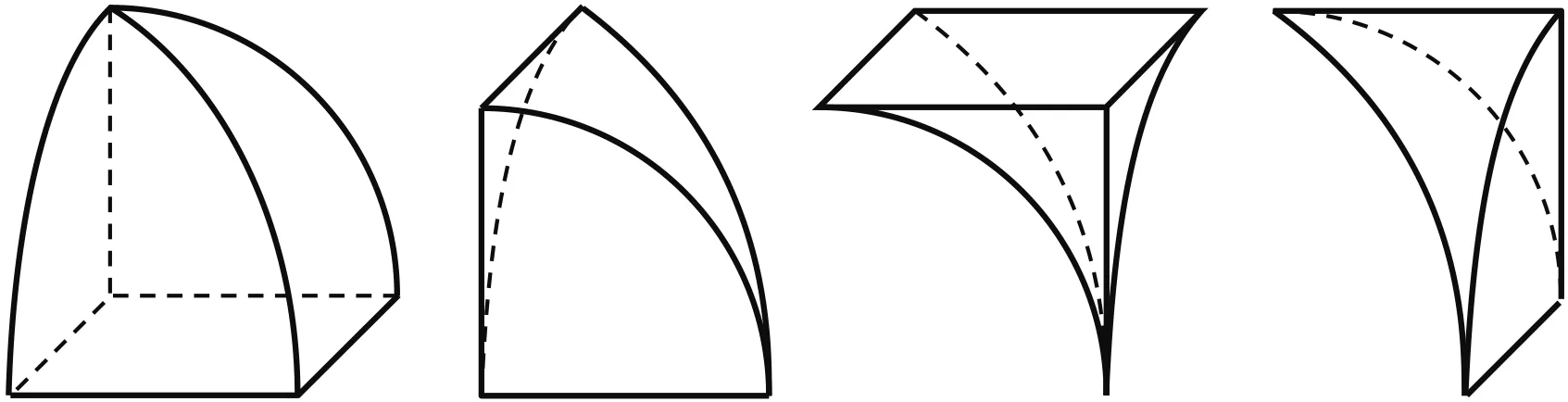
图8 立方体八分之一部分的构成

求三块“碎片”体积的尝试以失败告终．刘徽不无遗憾地说:“欲陋形措意,惧失正理．敢不阙疑,以俟能言者．”

图9 外棋与倒立阳马

正是刘徽的留白,引发了祖暅的发现．导致新知发现的思维是数学创造力的因素之一[4],我们将为这种思维所留的空间称为“发现之白”．

4 方法之白

在命题的证明或问题的求解上,一代代数学家从未停止过探索的脚步．面对过去的数学家所给出的某个命题的某种证明或某个问题的某种解法,追求真善美、富有好奇心和创新精神的数学家常常会问:还有更好的方法吗?这就是为什么同一个数学命题在历史上往往会有多种不同的证明．

欧几里得在《几何原本》中利用勾股定理(命题I.47)证明了钝角三角形和锐角三角形情形的余弦定理几何形式(命题II.12和II.13),17世纪荷兰数学家格雷戈里(Gregory of Saint-Vincent,1584—1667)思考了如下问题[5]:可否像欧几里得证明勾股定理那样,用面积的方法来证明这两个命题呢?如图10,在锐角三角形ABC三边上,分别作正方形ACEF,BCHG,AMNB,过顶点A,B,C分别作对边的垂线,垂足为I,K,D,交相应的正方形的另一边于点J,L,P．以全等三角形为媒介,可以证明长方形AIJF,BKLG的面积分别等于长方形AMPD,DPNB的面积．又以全等三角形为媒介,可以证明长方形JICE和HCKL面积相等,于是有c2=a2+b2-2a×CI,或c2=a2+b2-2b×CK,注意到CI=bcosC,CK=acosC,分别代入上面的等式,即得今天人们耳熟能详的三角形式的余弦定理结论．

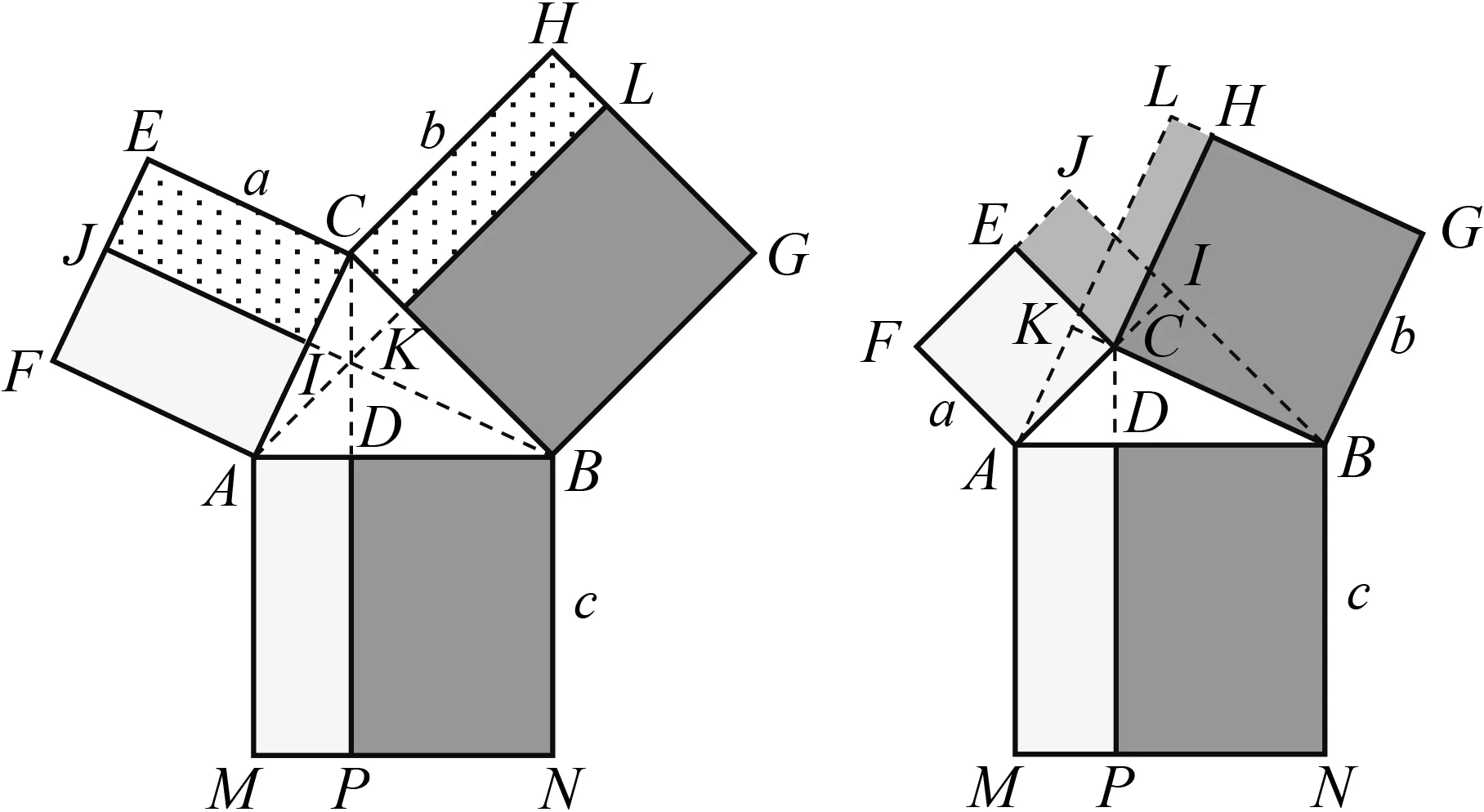
图10 锐角三角形情形的余弦定理的面积证法 图11 钝角三角形情形的余弦定理的面积证法

如图11,同理可证钝角三角形中的结论c2=a2+b2+2a×CI或c2=a2+b2+2b×CK．注意到CI=bcos(π-C),CK=acos(π-C),即得三角形式的余弦定理结论．

对于《几何原本》中的大量命题,如三角形内角和定理、等腰三角形性质定理、边边边定理、 勾股定理、黄金分割的 作图、圆内接正五边形的作图、线面垂直判定定理等等,后世数学家都有新的证明．可见,这部数学圣经为后世数学家留下了广阔的思维空间．“创造数学问题全新解法的能力”也是数学创造力的因素之一[4],我们将为 突破旧法、创造新法所留下的思维空间称为“方法之白”．

5 问题之白

没有问题,就没有数学的发展．数学史是数学问题的宝库,这个宝库是一代又一代数学家在漫长的过程中不断积累起来的．任何一个数学问题都可以成为人们设计新问题的出发点．

1617年,荷兰数学家斯内尔(W.Snell,1580—1626)解决了以下测量问题:如图12所示,已知三点A,B,C两两之间的距离,从观测点P处可以观测到点A,B,C,测得∠APB和∠APC的大小(分别记为α和β),求PA,PB,PC的长度．1692年,法国数学家波特诺(L.Pothenot,1650—1732)将上述问题改成求点P的位置问题,后人因此将“已知三点两两之间的距离以及观测所得两个视角,求观测点位置和观测点到已知点的距离”统称为“斯内尔-波特诺问题”(有时也被称为“地图问题”)．

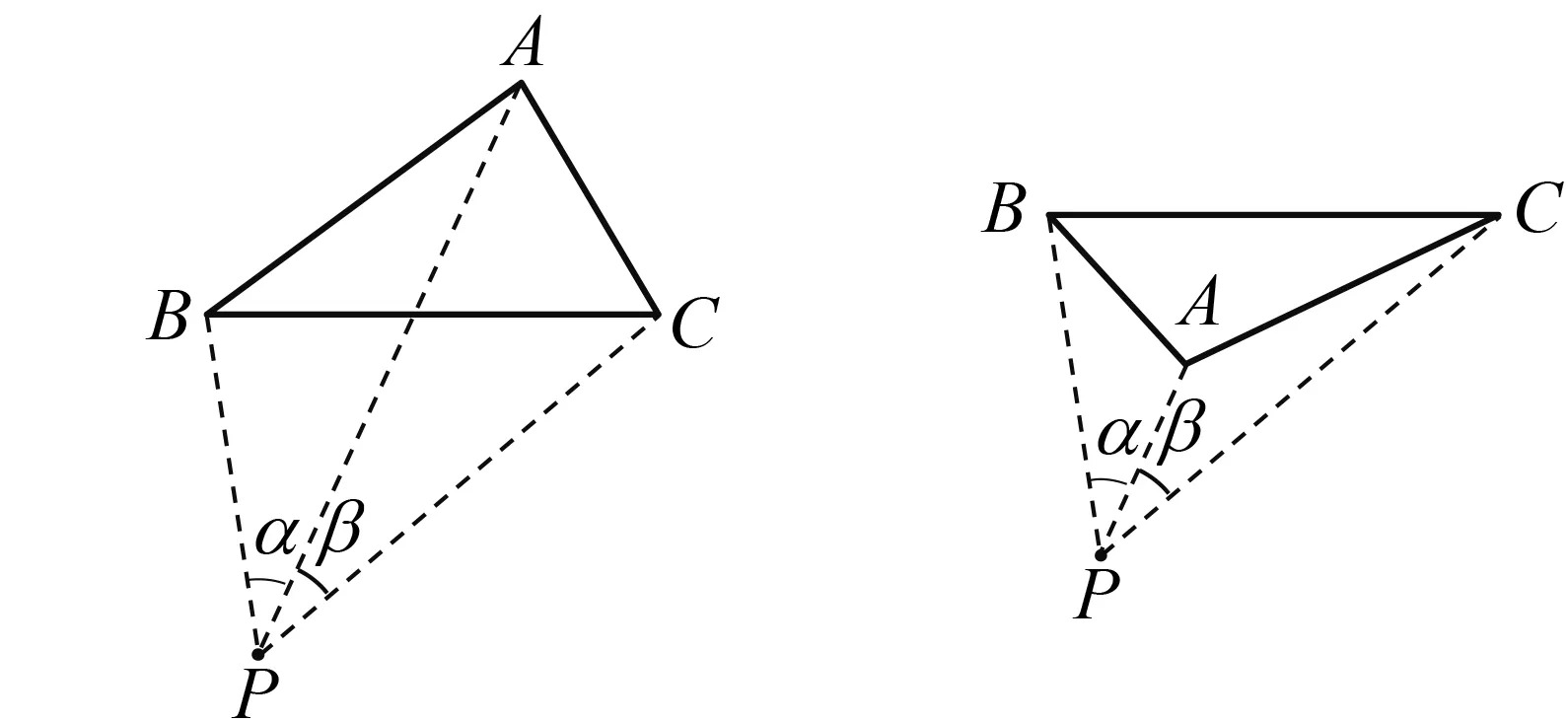
图12 斯内尔-波特诺问题1 图13 斯内尔-波特诺问题2

1671年,英国数学家柯林斯(J.Collins,1624—1683)再次对该问题进行了讨论[6]．柯林斯按照观测点P和三个已知点A,B,C的不同位置,将问题分成六类,除了斯内尔所考虑的图12所示的情形,另外五种情形如图13～17所示．

图14 斯内尔-波特诺问题3 图15 斯内尔-波特诺问题4

图16 斯内尔-波特诺问题5 图17 斯内尔-波特诺问题6

1845年,美国数学家肖菲尔德(N.Scholfeld)在其《高等几何学与三角学》中在斯内尔-波特诺问题的基础上,又提出新的问题[7]:

·如图18所示,已知三点A,B,C两两之间的距离,从点P可以观测到点B,A,Q,但不能观测到点C;从点Q可以观测到点C,A,P,但不能观测到点B．测得∠APB,∠APQ,∠AQC,∠AQP的大小,求PA,PB,PQ,QC,QA．

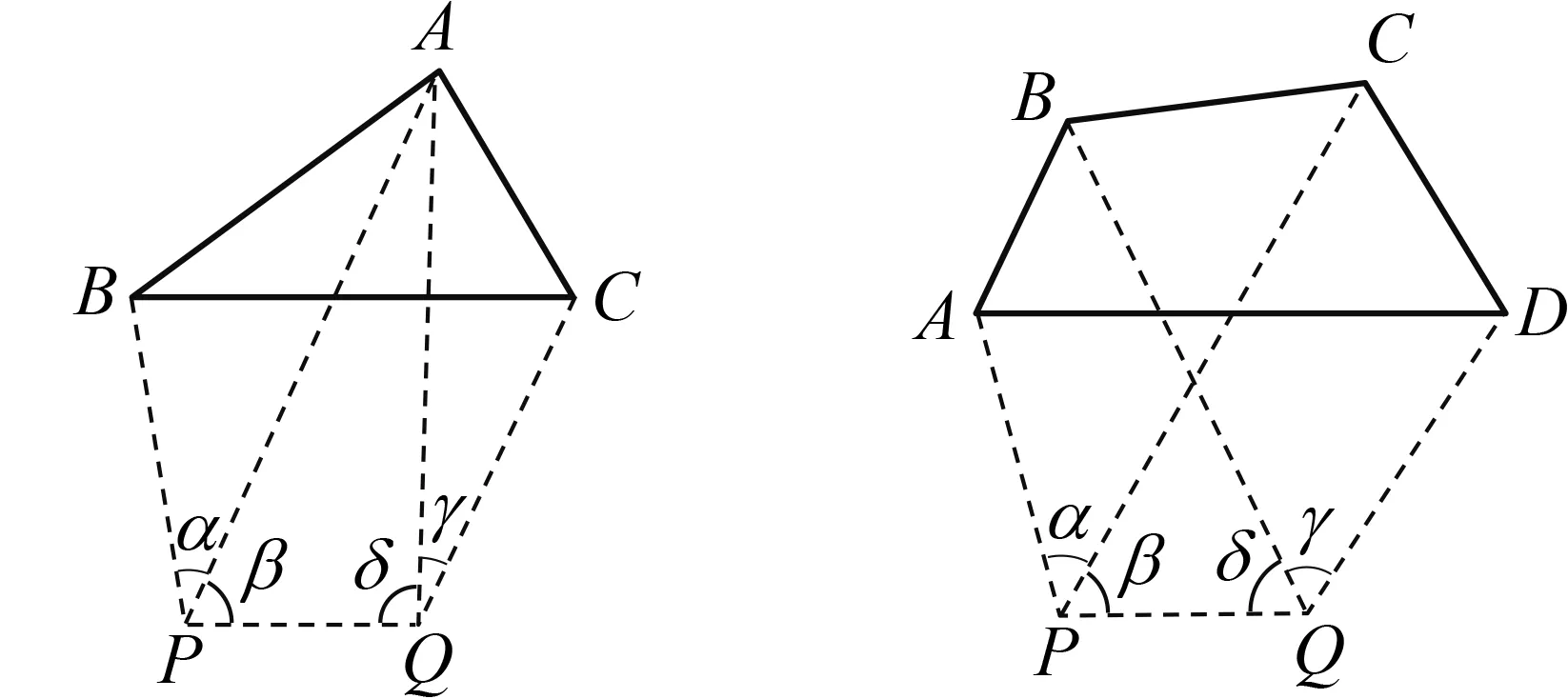
图18 斯内尔-波特诺问题的推广1 图19 斯内尔-波特诺问题的推广2

·如图19所示,已知四边形ABCD各边的长度以及各角的大小,从点P可以观测到点A,C,Q,但不能观测到点B,D;从点Q可以观测到点D,B,P,但不能观测到点C,A．测得∠APC,∠CPQ,∠DQB,∠BQP的大小,求PA,PC,PQ,QD,QB．

这里,柯林斯和肖菲尔德在斯内尔测量问题的基础上,采用条件操作策略(即改变原问题的条件而保留其所求目标)提出新问题．问题提出是培养数学创造力的有效途径之一[4],我们将为提出新问题而留出的思维空间称为“问题之白”．

6 结语

以上我们看到,从数学史上的典型案例中至少可以总结出“留白”的四类形式——论证之白、发现之白、方法之白和问题之白．可以断言,数学的历史就是留白与创新的历史:前人的失败是后人成功的阶梯,前人的思想是后人发现的钥匙,前人的结果是后人论证的目标,前人的方法是后人创新的源头,前人的问题是后人探索的起点．总之,正是有了前人的留白,才有了后人的创新,留白是创新的必要条件．

数学史上的留白与创新为留白创造式教学提供了思想启迪．

首先,在教学中,要培养学生的创新意识和创新能力,教师在教学中需要留白,教师的留白是学生创新的必要条件,因此,我们有必要倡导留白创造式教学．

其次,在教学中,教师可以设计恰当的探究任务,留出发现之白,引导学生创获新知;留出论证之白,促使学生探寻因果;留出方法之白,助力学生另辟蹊径;留出问题之白,培养学生提问能力．

再次,数学史本身也为留白创造式教学提供了取之不尽、用之不竭的问题和方法,是留白创造式教学设计、实施和评价的思想源泉．