星间激光通信机光轴指向误差源分析与补偿控制

刘政麟，汪逸群

(之江实验室，杭州 311121)

0 引 言

通信卫星是构建天地一体化全球通信网络的重要载体,星间激光通信技术是现代卫星通信网络的重要组成部分[1]。相比作为传统通信载体的微波,激光的波长更短、相干性更好,使卫星激光通信具有通信容量大、精度高、重量轻、功耗低、体积小等优点,可以实现更大容量、更高速率的信息传输[2-6]。星间激光通信机是搭载在卫星上的小型化激光通信终端,用于实现星间激光通信链路的建立和数据通信。随着国际航空航天技术的发展和对新一代通信技术的要求,美、欧、日等发达国家已进行了诸多卫星激光通信技术的研究与试验[7-12],我国也从20世纪90年代开始加快了对卫星激光通信技术的研究步伐[6,13-15]。

高精度的光轴指向与跟瞄系统,是星间激光通信链路建立和正常工作的关键,对空间光通信光轴误差的研究一直是相关研究领域内的重点[16-21]。影响链路建立的误差主要为卫星姿态误差和通信机光轴指向误差。较大的误差会使激光通信机无法准确地捕获和跟踪目标,无法建立稳定的星间通信链路,导致通信的不稳定,甚至中断。卫星姿态误差需要根据星地标校进行修正,而通信机光轴指向误差可以在地面根据测试结果提前完成补偿。需要对激光通信机光学系统的误差源进行分析,并设计补偿方案来降低光学误差对光轴指向精度的影响。

本文主要对一集约化设计的星间激光通信机光学系统进行了详尽的误差源分析,并提出基于粗跟踪校正、精跟踪校正的综合补偿方案来修正后光路误差对指向精度的干扰。结果表明,补偿后的相机处光斑位置偏差有了显著减小,可以满足建立稳定星间激光通信链路的要求。

1 激光通信机光学系统的误差模型

1.1 激光通信机的结构设计及误差角定义

本文中的星间激光通信机光学系统采用了基于二维摆镜的扫描装置、跟瞄机构和通信机构共用光电探测器的集约化设计,具体结构如图1所示。外来入射光线经二维摆镜反射后照射到主镜上。主镜与次镜为具有不同曲率半径的一组离轴双反射镜,组成一个望远镜系统。之后,光依次经精跟踪振镜、折转镜、分镜反射,入射到由4个具有不同焦距的厚透镜组成的透镜组上。出射光再经平面反射镜反射,入射到精跟踪相机上,完成外来光在相机上的成像。通信接收路、通信发射路的终点位于精跟踪相机路关于分镜、分色镜的共轭点处,因此,实现对精跟踪相机路光斑位置误差的控制,就能保障通信接收路和通信发射路的精度要求。

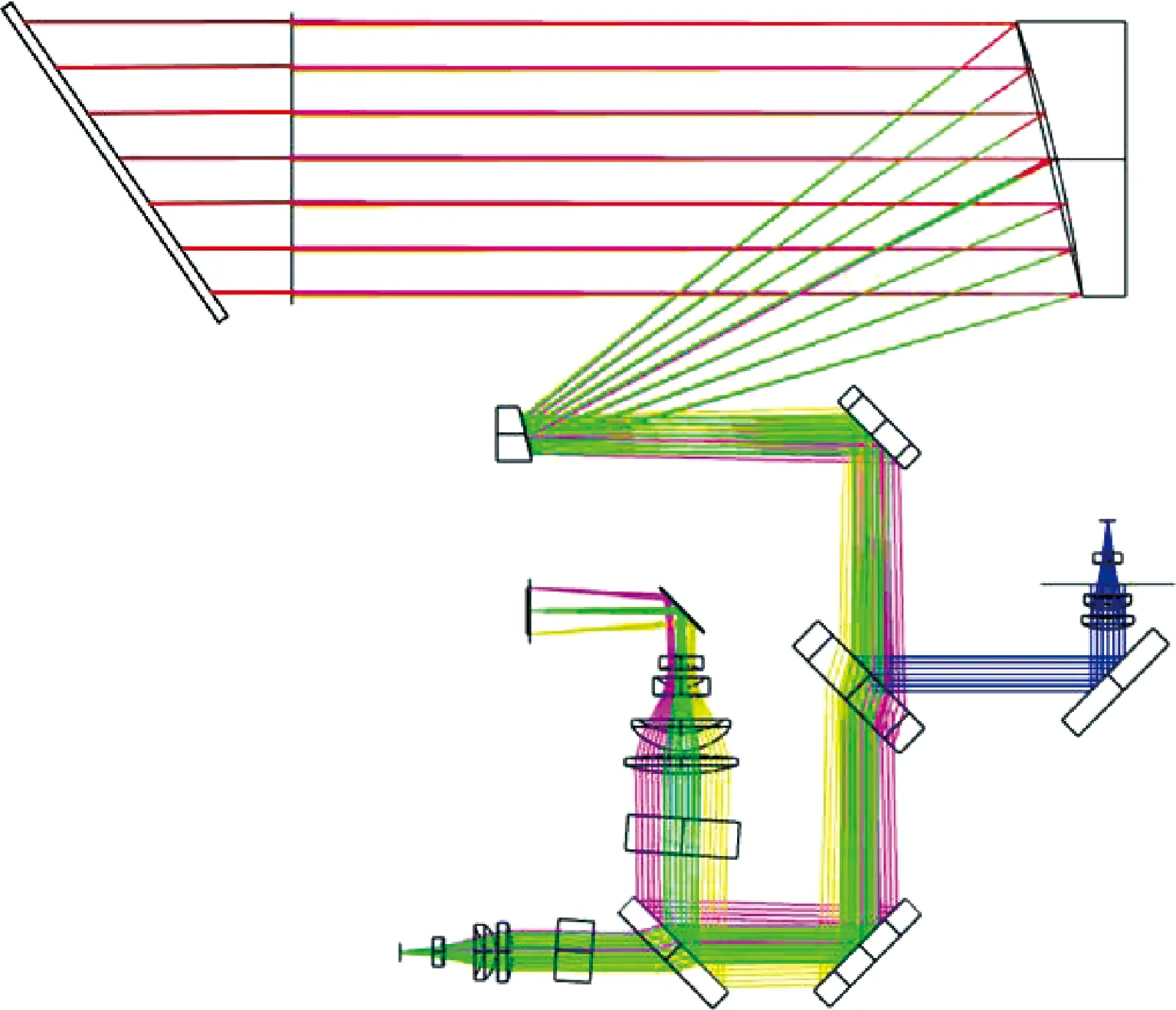
图1 激光通信机光学系统的整体结构Fig.1 Optical system structure of the laser communicator

对精跟踪相机路建立数学模型,首先需要构建坐标系。将通信机光学系统的基准坐标系称为终端坐标系,其z轴正方向从主镜指向二维摆镜;x轴正方向从精跟踪振镜指向折转镜;y轴与x轴和z轴共同构成右手系,正方向垂直纸面向外。各个元件的误差也基于与终端坐标系的偏差来确定,z′轴与z轴正方向的夹角定义为俯仰误差角φi0,z′轴在x-y平面内的投影与x轴的夹角定义为方位误差角ψi0,i为精跟踪相机路元件从外到内的编号。对于二维摆镜额外存在一个轴系正交误差,为俯仰轴与x-y平面的夹角,如图2中角θs所示。

图2 元件误差角的定义Fig.2 Definition of the component error angle

1.2 精跟踪相机路中各元件的作用矩阵

精跟踪相机路中,对外来光线方向矢量有影响的元件依次有二维摆镜、主镜、次镜、精跟踪振镜、折转镜、分镜、透镜组、相机前反射镜,最终将光入射到精跟踪相机处。需要计算路径中每个元件对光的作用矩阵,从而得到相机处光斑的位置与各元件误差的关系。

二维摆镜是一个可调元件,具有俯仰角和方位角两个旋转维度。设入射光单位矢量为r0,目标出射光单位矢量为r′1=[0, 0, -1]T,则二维摆镜目标法线方向为

(1)

式中:fI(r)表示与矢量r同向的单位矢量。将F′1m转换至球坐标系,得到二维摆镜目标法线方向对应的俯仰角φ′1和方位角ψ′1。设摆镜的初始法线方向俯仰角为π,方位角为0,指向z轴负方向,则二维摆镜需要转动的角度为

φ1=φ′1-π;ψ1=ψ′1

(2)

对实际元件进行转动,采用在三维空间中绕某个轴转动一定角度的方法。考虑在三维空间直角坐标系中某点绕任意轴的转动,其转动函数的矩阵表示为

(3)

式中:nx=-sinψcosθ,ny=cosψcosθ,nz=sinθ分别为旋转轴单位方向矢量在x,y,z方向上的分量;φ为某点绕转轴转过的角度;ψ为转动方向对应的方位角;θ为转轴与x-y平面的夹角。

二维摆镜存在角度失调误差φ10,ψ10,转轴失调误差φ1a,ψ1a和轴系正交误差θ1p,如图3所示。根据式(3),转动后的二维摆镜实际法线方向矢量为

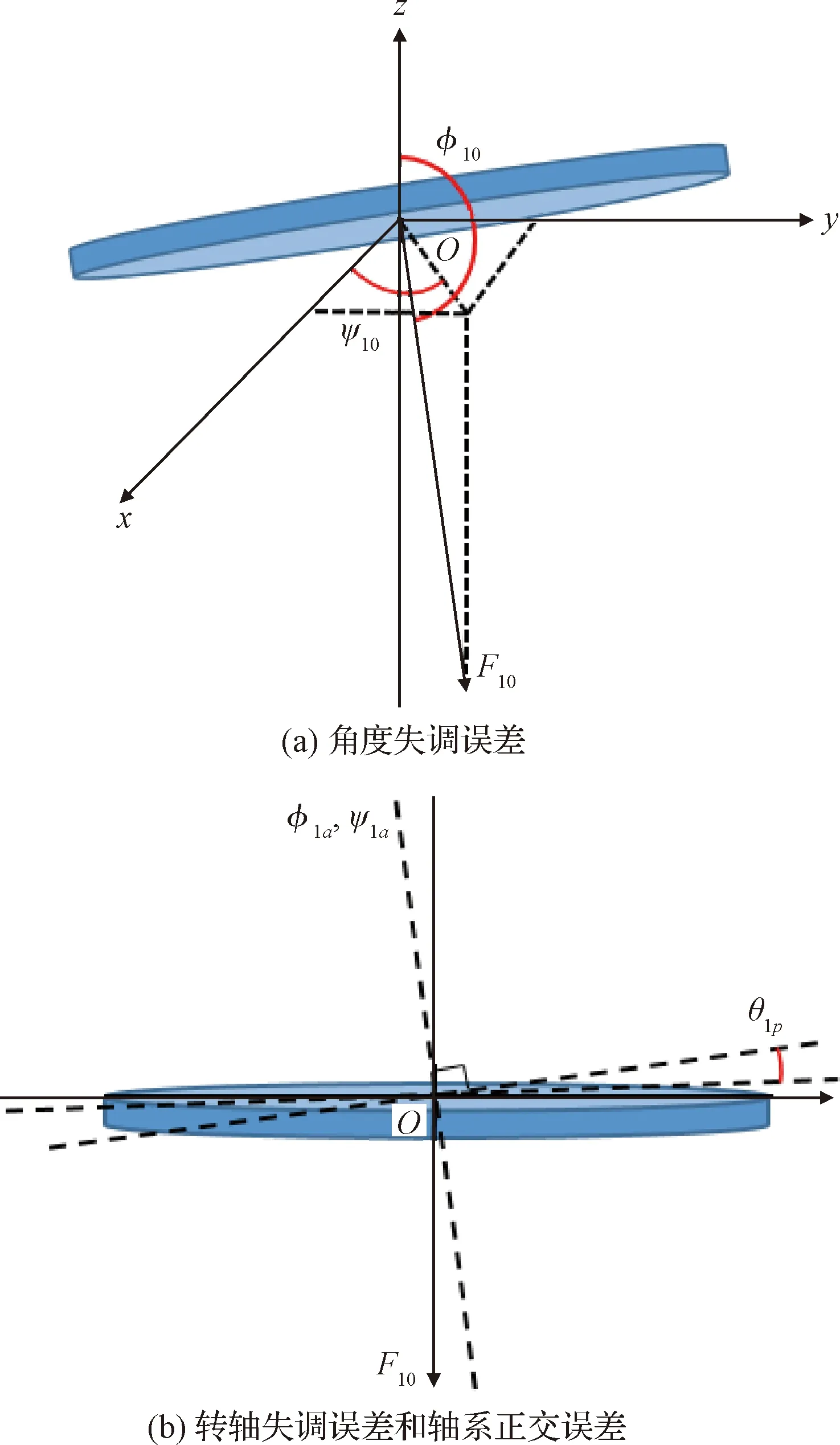
图3 二维摆镜存在的误差。Fig.3 Errors of two-dimension waving mirror

F1=Tr(φ1a,ψ1a, 0)Tr(φ1,ψ1,θ1p)Rz(ψ1)·

(4)

式中:Rz(ψ)表示绕z轴转动ψ角的矩阵。

根据反射矩阵,可以得到转动后的二维摆镜的矩阵描述

(5)

主镜和次镜为一对离轴球面反射镜,共同构成了一个望远镜系统。由于在安装过程中,主镜和次镜是先独立安装成望远镜系统后再安装进光学系统,因此,为了计算方便又不失一定的准确性,将两个离轴球面镜组成的望远镜系统进行整体考虑和分析,忽略望远镜系统的内部误差,只考虑整体误差。对于图1中的望远镜系统,放大倍率为η=1/8,理论入射光线与出射光线保持平行。设望远镜系统的俯仰角、方位角误差分别为φ230,ψ230,则该望远镜系统的作用矩阵为:

(6)

精跟踪振镜、折转镜与分镜为三个平面反射镜,其中折转镜与分镜为固定元件,精跟踪振镜为可调元件。由于精跟踪振镜的转动幅度很小,转轴误差和轴系正交误差可以忽略不计。因此,三者均只存在一个角度失调误差。对于具有角度失调误差φ40,ψ40的精跟踪振镜,在终端坐标系中理想法线方向指向z轴正方向偏x轴正方向π/4处,则对入射光线的作用矩阵为

(7)

对于具有角度失调误差φ50,ψ50的折转镜,在终端坐标系中理想法线方向指向z轴正方向偏x轴负方向π/4处,则对入射光线的作用矩阵为

(8)

对于具有角度失调误差φ60,ψ60的分镜,在终端坐标系中理想法线方向指向z轴负方向偏x轴负方向π/4处,则对入射光线的作用矩阵为

(9)

根据式(1)至(9),入射光由分镜出射时的光单位方向矢量为

r6=T6T5T4T23T1r0

(10)

透镜组由四个厚透镜组成,各自具有不同的焦距。透镜组存在的误差主要为失调误差,包括透镜的位置失调误差和角度失调误差。传统计算透镜组的方法为引入等效焦距,仅将透镜组看作一个透镜,无法精确反映因光入射位置或角度偏差导致的出射光矢量变化。为了提高光位置和方向的准确性,创造性地引入矩阵光学方法来描述后光路透镜组[22]。由于透镜是中心对称元件,在分析时分解为互相垂直的两个方向的分量。在图1所示的光学系统中,理想情况下光经透镜组的传输方向为x轴负方向,分别研究x-y平面和x-z平面内的透镜矩阵。对于非傍轴情况,即元件存在一定的失调误差时,元件矩阵需要拓展成4×4的矩阵。根据矩阵光学的失调理论,一个失调厚透镜在某个方向上的矩阵表示如下

(11)

(12)

式中:l为透镜厚度;R1,R2分别为厚透镜前后面的曲率半径;n为厚透镜折射率;ε,ε′分别为失调位置和失调角度。设两厚透镜之间的距离为d,视为自由空间,其对应矩阵表示为

(13)

根据式(11)～(13),可以直接把透镜组用矩阵进行描述。由4个厚透镜构成的透镜组光学系统在单方向上的矩阵可表示为透镜矩阵与自由空间矩阵的连续相乘

MT=Md1011MT10Md910MT9Md89MT8Md78MT7Md67

(14)

在失调系统中,需要对光参数进行扩张以对应4×4的光学矩阵运算。在这里直接给出光经透镜组的矩阵表达式。在x-y平面和x-z平面内分别有

(15)

入射光的偏移角度可以由分镜出射光得到

(16)

入射光的偏移位置可以由次镜后的光线在每段传输过程中的位移进行累加得到

(17)

式中:r的下标表示编号对应元件的出射光单位矢量在某个方向的分量;l的下标表示编号对应两个元件之间的光程。将式(16)～(17)代入式(14)～(15)计算,即可得到透镜组出射光在x-y平面和x-z平面内的出射位置r10y,r10z和出射角度θ10y,θ10z。

相机前反射镜为一固定的平面反射镜,存在角度失调误差φ110,ψ110。将经透镜组出射的光线r10转换回终端直角坐标系中的矢量

(18)

则机前反射镜对入射光线的作用矩阵为

(19)

与计算透镜组入射光位置的方法类似,仍通过分段计算累加的方式得到光斑在精跟踪相机处位置坐标,具体表达式为

(20)

式中:d11c为相机前反射镜到精跟踪相机感光平面的距离。这样,就建立了通信机后光路系统的数学模型,各项误差可以通过修改对应元件的矩阵来体现。

2 蒙特卡洛方法分析因安装误差造成的光轴指向误差

根据精跟踪相机路中的元件种类,将系统误差分为六类,分别为透镜位置失调误差Δrlens、二维摆镜角度失调误差Δφ10、光学元件角度失调误差Δφm、二维摆镜转轴失调误差Δφ1a、二维摆镜轴系正交误差Δθ1p、二摆镜转角误差Δθ1。为了研究每项误差对光轴指向精度的影响,分别单独引入某类随机误差值(其他类型误差不存在),采用蒙特卡洛方法,在MATLAB中计算相机处的光斑位置坐标。每项误差取值106次,取值方式为最大误差范围内的均匀分布,所得统计结果如表1所示。

表1 各类误差导致的光斑偏移量Table 1 Spot offset caused by various errors

从表1可以看出,在精跟踪相机路存在的各类误差中,光学元件角度失调误差Δφm、二维摆镜转轴失调误差Δφ1a、透镜位置失调误差Δrlens对光斑位置的影响较大,而二维摆镜轴系正交误差Δθ1p和二维摆镜转角误差Δθ1带来的影响较小。在通信机整机的装调过程中,需要着重控制对光轴指向影响较大的几类误差,防止光斑位置偏差过大。实际后光路系统中各项安装误差同时存在,对光轴指向精度影响显著,需要进行校正,以满足实际应用的需求。

3 误差校正矩阵修正安装误差

在激光通信机工作时,由于光学系统误差的存在,光轴指向存在偏差,表现为精跟踪相机处的光斑不处于相机中心,无法对目标进行准确的瞄准和跟踪。因此,需要对光学系统中存在的误差进行补偿,尽量减小光学误差对相机处光斑位置偏移的影响。重新定义相机零点位置,使入射光斑初始位置位于重置后的零位,可以校正安装误差造成的误差初值。在此基础上,进一步提出误差校正矩阵方法,用于校正任意方向的安装误差。该方法主要分为粗跟踪误差校正矩阵和精跟踪误差校正矩阵。

3.1 粗跟踪误差校正矩阵

理想情况下,入射光经二维摆镜反射出的光在终端坐标系方向的单位矢量为[0, 0, -1]T。由于二维摆镜自身存在位置失调误差φ10,ψ10,转轴失调误差φ1a,ψ1a和轴系正交误差θ1p,实际系统中,二维摆镜的出射光方向矢量与目标矢量存在一定的偏差。为了确定相机处光斑位置与二维摆镜反射光方向矢量的关系,构造直接入射到主镜的光线,其俯仰角为π±15″,方位角为0～2π,则该光线在相机处光斑位置如图4所示。光斑呈圆环状分布,光斑位置距原点的距离与构造光线的俯仰角有关,而光斑位置在相机处坐标的方位角与构造光线的方位角有关。光学系统其他元件的固定误差可以忽略不计。由此可以得到相机处光斑位置与二维摆镜反射光方向矢量的近似关系

图4 沿不同方向入射到主镜的光在相机处的光斑位置Fig.4 Spot position of beams incident on the main mirror in different directions at the camera

(21)

式中:Δφ, Δψ表示二维摆镜反射光较终端坐标系z轴负方向的俯仰角和方位角误差;Δx, Δy表示相机处光斑在x和y方向上的坐标;nR为粗跟踪比例系数,由光学系统构造决定。

粗跟踪校正过程中,入射光方向单位矢量r0为已知量,根据式(21)计算出的二维摆镜出射光方向矢量,可以得到二维摆镜法线的方向矢量为

(22)

对于理想情况,二维摆镜出射光沿z轴负方向,则此时二维摆镜法线的方向矢量为

(23)

根据式(22)～(23),将二维摆镜法线方向单位矢量转化到球坐标系,可以得到实际法线和理想法线各自的俯仰角和方位角,分别为φ1,ψ1和φ1i,ψ1i,二者的差值为

Δφ1=φ1i-φ1, Δψ1=ψ1i-ψ1

(24)

在装调完成的确定系统中,式(24)计算得到的二维摆镜法线方向角差值只与入射光方向单位矢量r0有关,Δφ1和Δψ1即为二维摆镜的补偿转角。这样,可以根据r0计算得到二维摆镜的理想俯仰角φaim1和理想方位角ψaim1。以φaim1和ψaim1为矩阵的行坐标和列坐标,对应角度时的二维摆镜补偿转角Δφ1和Δψ1为相应矩阵元的值,构建粗跟踪误差校正矩阵。在粗指向机构根据入射光方向进行第一次转动的基础上,读取粗跟踪误差校正矩阵相应矩阵元,二维摆镜额外转动补偿转角,即可达到校正后光路安装误差的效果。

3.2 精跟踪误差校正矩阵

受限于粗指向机构转动频率,粗跟踪误差校正矩阵无法精确校正后光路安装误差,需要精跟踪振镜辅助校正。精跟踪振镜具有高精度、高频率的特点,沿x和y方向的旋转角分别为φ4x和φ4y。构建精跟踪误差校正矩阵的关键同样在于如何计算得到与转动角度对应的补偿转角。

首先随机产生了一组固定安装误差,用于模拟某确定后光路系统。此时,相机上光斑初始位置处于第二象限。令精跟踪振镜的x和y方向转角在一定范围内循环变化,可得图5所示的光斑位置分布,每个点对应一组精跟踪振镜转角。光斑在x轴方向的位置对应精跟踪振镜绕y轴的转动角度,在y轴方向的位置对应精跟踪振镜绕x轴的转动角度。由于精跟踪振镜的初始法线位置为z轴正方向偏x轴正方向π/4,因此,对于沿振镜的x和y方向转动同样的角度,相机处光斑在y和x方向的移动距离是不同的,经计算可得

图5 精跟踪振镜转动不同角度时,相机处的光斑位置Fig.5 Spot position at the camera with different rotation angles of fine tracking galvanometer

(25)

精跟踪振镜的转动角度很小,式(25)可以近似为

(26)

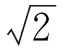
图5中随精跟踪振镜转动变化的光斑位置分布近似是一个等间距矩形点阵,很自然可以想到,精跟踪振镜的补偿角度只与光斑初始偏移位置有关。读取原点处数据点对应的精跟踪振镜沿x,y方向的旋转角度,就可以得到精跟踪振镜所需额外旋转的补偿角。在精跟踪振镜转动角度较小时,给出对应的近似关系

(27)

式中:Δx, Δy表示相机处光斑在x和y方向上的坐标;nF为精跟踪比例系数,同样由光学系统构造决定。以质心坐标偏差量Δx和Δy为矩阵的行坐标和列坐标,对应质心坐标时的精跟踪振镜转角φ4x和φ4y为相应矩阵元的值,构建精跟踪误差校正矩阵。在激光通信机运行时,根据粗跟踪校正后的相机处光斑的位置坐标,直接读取精跟踪误差校正矩阵对应矩阵元处的精跟踪振镜转角,即可转动精跟踪振镜,完成对光轴指向误差的校正。

3.3 误差校正后的光轴指向精度

下面同样采用蒙特卡洛方法模拟误差校正后的光轴指向精度。考虑一个具有随机误差的光学系统,各误差的最大取值与表1中取值相同,入射光俯仰角范围为60°～120°,方位角范围为0～2π。由于选择的误差范围较大,相机处的光斑偏离相机中心的距离会较远。在MATLAB中,每一项误差在其范围内取均匀分布的随机值,则每一组误差值对应一个相机处的光斑位置。该通信机系统中,相机单像素尺寸为15 μm×15 μm,折合角度偏差为8.5 μrad。取2000组随机误差,观察相机处光斑位置的分布。

图6(a)展示了不进行任何补偿时相机处的光斑位置分布图。相机处光斑距离相机中心的最大偏移位置接近3 mm,对应角度偏差约1.7 mrad,此时光轴指向误差极大,无法满足链路建立的需要。

图6(b)展示了重新定义相机零点位置且粗跟踪误差校正矩阵补偿后的相机处的光斑位置分布图。此时,相机处光斑的偏移量显著减小,距中心最大值约0.08 mm,对应角度偏差约45 μrad,对安装误差造成的光轴指向偏差有显著的校正作用,已经达到对粗跟踪补偿精度的要求。

图6(c)展示了在6(b)基础上进一步进行精跟踪误差校正矩阵补偿后的相机处的光斑位置分布图。相机处光斑的偏移量进一步减小,基本被限制在了0.0005 mm之内,对应角度偏差约0.3 μrad。这表明经过粗跟踪和精跟踪两级误差校正矩阵补偿后,相机处的光斑位置都会集中于中心像素处。此时的通信机后光路具有极高的光轴精度,可以用于实现星间链路的稳定建立,满足激光通信的要求。

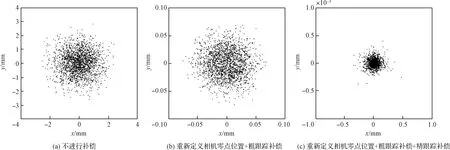
图6 不同补偿且存在随机误差时,相机处光斑位置。Fig.6 The spot position distribution at the camera with random errors under different compensation situations

为了更精确地给出综合补偿方案对光轴精度的校正作用,对上述给出的补偿情况,分别计算106组随机误差值,将对应光点位置误差数据列入表2中,可以更加直观地展示综合补偿对相机处光斑位置偏差情况的改善。随着补偿的依次运行,相机处光斑越来越集中于中心,表明光轴的指向精度不断提高,表明粗跟踪和精跟踪误差校正矩阵能够有效补偿后光路安装误差,显著提高激光通信机光轴指向精度。

表2 不同补偿情况下,相机处的光斑在存在随机误差时的位置统计Table 2 Statistics of spot position at the camera with random errors under different compensation situations

由于影响粗跟踪和精跟踪补偿角的因素只有精跟踪相机路的光学结构以及相机处的光斑位置,该方法适用于任何方向的入射光。太空中卫星存在的抖动,可以等效为入射光方向的抖动,误差校正矩阵同样。校正过程中,只需要根据相机处光斑位置读取补偿表,获得粗跟踪和精跟踪的补偿转角,在自身当前转动位置处叠加额外转动即可。根据相机上光斑位置的不断变化进行实时闭环补偿,不断将光斑向相机中心补偿,校正光轴指向误差,保持对目标的高精度瞄准和跟踪。这一方法大大降低了通信机扫捕跟程序的运算量,节约了运算时间和负载,有利于提高跟踪响应频率和速度。

4 粗跟踪误差校正矩阵修正安装误差实机测试

在实际的激光通信机系统中,粗跟踪系统由于转动范围大,是系统光轴误差的主要来源。在超净间中使用项目组设计制造的60 mm激光通信机初样件进行粗跟踪误差校正矩阵修正安装误差的实机测试,测试装置如图7所示。60 mm激光通信机安装在二维转台上,可以通过转台的转动改变入射光的方向。地检装置端设置激光光源,用于入射到激光通信机判断光轴指向偏差。放置在二维转台上的通信机在初始位置接收到的光斑位置设为光斑零点。二维转台转动时,二维摆镜反向转动,补偿因转台转动导致的光轴偏移,使光轴始终对准光源。由于二维摆镜存在安装误差,相机处光斑质心坐标会产生偏移,图8展示了转台方位角从-50°到+50°、俯仰角从-15°到+15°的范围内,方位角每间隔10°、俯仰角每间隔5°取一个点,得到的光斑质心坐标偏移的像素值。

整体趋势上,转台转动角度越大,二维摆镜对应的转动角度也要增大,光轴的偏移量就越大。方位角负侧偏移量比正侧更大,这与具体的光机装调情况相关。根据每个点处二维摆镜转动角度和光斑偏移量,计算得到粗跟踪误差校正矩阵,图9给出每一个样本点处对应的二维摆镜俯仰角和方位角的补偿值。补偿值的单位为二维摆镜的码值,二维摆镜在360°范围内共对应224个码值。如方位角-50°、俯仰角-15°时的补偿角为107,348,则需要将二维摆镜的俯仰方向码值增加107,方位方向码值增加308,转动后的位置即为经误差校正矩阵修正后的二维摆镜位置。在每个样本点处,根据误差校正矩阵将二维摆镜位置修正后,得到补偿后光斑质心坐标偏移量,如图10所示。

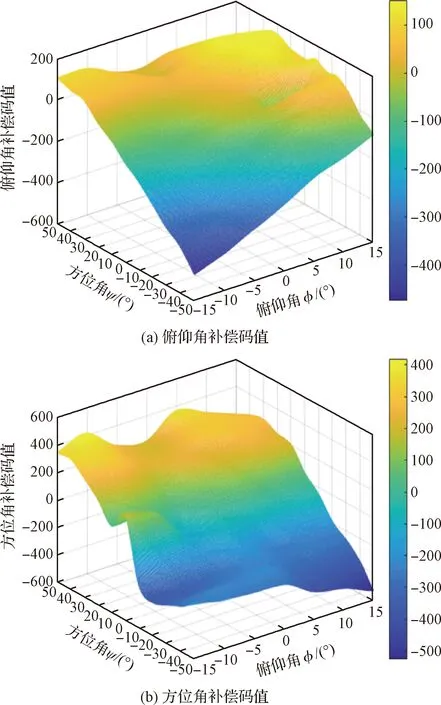
图9 不同俯仰、方位角时,二维摆镜的补偿角码值Fig.9 Compensation angle code value of swing mirror with different elevation and azimuth

图10 不同俯仰、方位角时,补偿后的光斑偏移量Fig.10 Spot offset after compensation with different elevation and azimuth

显然,经过粗跟踪误差校正矩阵修正后,光斑的质心坐标偏移量显著减小,控制在相机中心±1.5个像素之内,对应光轴指向精度偏差约13 μrad。这表明误差校正矩阵对光轴误差有明显的修正作用。进一步地,为了验证误差校正矩阵在任意角度处的可行性,选择10组随机的转台俯仰角和方位角,并选择误差校正矩阵中临近的4个样本点的值做线性叠加,得到对应的二维摆镜补偿角,并观察补偿后的光斑质心坐标情况,如表3所示。根据随机点线性叠加修正结果,修正后最大的光斑质心偏移量为(1,-3)像素,表明粗跟踪误差校正矩阵对转动范围内的任意角度均有效,对校正主要因后光路安装误差导致的光轴指向偏差作用明显,减小光斑质心坐标偏移量,大大降低了光机后光路系统误差对激光通信的影响。

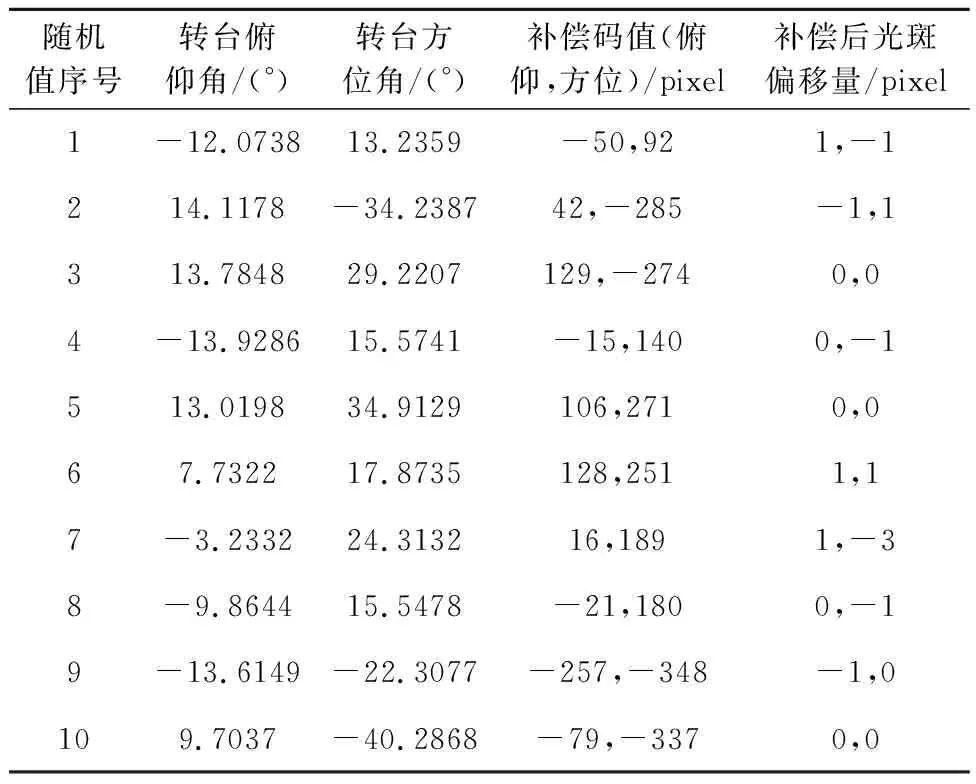
表3 随机俯仰方位角时,补偿后的光斑偏移量Table 3 Pixels of spot offset after compensation with random elevation and azimuth

5 结 论

本文根据星间激光通信机小型化的要求,对一通信发射-接收共光路的集约化设计激光通信机的光学系统进行了误差源分析,并提出了校正因安装误差导致的光轴指向偏差的误差校正矩阵。通过引入矩阵光学方法,提高了计算透镜组误差的准确性。采用蒙特卡洛方法模拟各安装误差对光轴指向精度的影响,结果表明在装调过程中需要重点控制光学元件角度失调误差、二维摆镜转轴失调误差、透镜位置失调误差等影响较大的误差种类。基于粗跟踪和精跟踪误差校正矩阵的修正方案可以有效校正安装误差对光轴指向的影响,修正后的精跟踪相机处的光斑质心坐标已经满足星间激光通信链路的建立和稳定运行的需要。粗跟踪误差校正矩阵修正光轴指向精度的实机测试验证了误差校正矩阵方法的准确性和可行性。本文建立的激光通信机光学系统误差源数学模型提高了对后光路光学误差的分析精度,有助于提高装调质量和效率;误差校正矩阵方法有效修正因安装误差导致的光轴指向偏差,满足激光通信机的工作需要,同时节约了通信机系统的运算资源,提高了跟踪响应频率;粗跟踪误差校正矩阵的实机测试证实了校正矩阵结合线性插值补偿法可以实现对任意角度的误差补偿,大大简化了通信机误差补偿算法,对实现星间激光通信具有相当的实用意义。