GEO混合推力机动目标跟踪IMM算法

王常虹，张大力，夏红伟，马广程

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引 言

地球静止轨道(GEO)卫星的轨道周期与地球自转周期一致,具有对地覆盖区域广、星下点轨迹固定等特点,在通信、遥感、气象、数据中继等领域发挥着重要作用,是极为宝贵的空间资产[1]。然而,随着在轨空间目标数量的不断攀升和空间安全形势的风云变幻,GEO环境愈加拥挤和复杂,亟需发展天基态势感知技术来应对潜在的安全风险[2-4]。其中,对具备机动能力的空间目标的稳定跟踪是最具挑战性的问题之一[5-6]。特别对于无法提供有效信息的非合作目标,由于机动大小和时间通常先验未知,目标速度的突变会导致传统基于目标无机动状态设计的跟踪算法性能退化甚至发散,严重时会丢失目标导致任务失败[7]。

为了解决机动目标跟踪问题,国内外学者开展了广泛的研究工作,相关成果可大致分为单模型方法和多模型方法。单模型方法采用单一模型,研究重点在于滤波器的改进。当目标发生未知机动时,滤波器估计值将偏离真实值,若能提高其对未知输入的处理能力使其对偏差不敏感,那么可避免滤波器发散[8]。周东华等[9]在扩展卡尔曼滤波(Exte-nded Kalman filter, EKF)算法中引入一种渐消因子(也称衰减因子),利用残差序列中的有效信息提高对过程参数变动的鲁棒性,并进一步提出一种强跟踪卡尔曼滤波(Strong tracking Kalman filter, STKF)算法,引入了软化因子使状态估计更加平滑,对机动目标的模型不确定性具有一定的鲁棒性[10]。在此基础上,Jwo等[11]提出一种用于GPS导航处理的自适应模糊STKF算法(AFSTKF),采用模糊逻辑实现了软化因子的在线调整,改善了STKF的发散问题。刘玉磊等[12]在Quadrature卡尔曼滤波(QKF)算法中引入渐消因子,并将其用于无源机动目标跟踪问题,以增加计算量为代价提高了对系统突变状态的跟踪能力。Wang等[13]提出了一种用于跟踪机动目标的自适应鲁棒无迹卡尔曼滤波(ARUKF)算法,通过在协方差预测过程引入基于新息序列正交原理计算的衰减因子,降低了动力学模型误差,提高了算法的跟踪性能。Zhang等[14]在容积卡尔曼滤波(Cuba-ture Kalman filter, CKF)算法的递归过程中引入时变因子,使滤波增益与量测值同时更新,提出了基于强跟踪方法的CKF算法(STCKF),提高了CKF算法对状态突变的处理能力。Li等[15]通过引入一个改进先验概率密度函数来解决建模不确定性问题,并将辅助截断粒子滤波与自适应最小二乘法相结合,用于处理仅测角机动目标跟踪问题,取得了比传统粒子滤波算法更优的性能。Jiang等[16]提出了一种基于归一化残差正交性原理的强跟踪滤波器,提高了算法对状态突变的敏感度,对于脉冲机动较小的情况比传统方法有更好的跟踪性能。

由于空间目标机动情况复杂,单一模型很难充分描述其状态演化,这极大限制了单模型方法的应用,因此以交互多模型(Interactive multiple model, IMM)算法为代表的多模型方法受到越来越多的关注[17]。IMM算法采用多个模型来匹配目标的运动状态,通过相应的滤波器对每个模型独立进行估计,模型间采用转移概率进行交互,具有很强的适应性,且实现较为方便,得到了较为广泛的应用[18]。Lee等[19]通过将机动目标建模为多模型跳变Markov系统,并采用轨道根数对每个模型进行描述,实现了对目标机动的跟踪估计,但受量测噪声影响,有一定几率发生机动误检。进一步,Lee等[20]提出一种基于状态依赖转移概率的机动目标跟踪方法,在转移概率计算中引入了目标脉冲机动的发生条件,因而可以更准确地预测目标机动,需要注意的是该方法需要对目标特定机动行为预先设置相应的跳跃条件。Manish等[21]提出一种概率数据关联方法对基于状态依赖的转移概率进行修正,降低了算法对目标机动的误检率。Goff等[22]针对非合作机动目标地面跟踪问题,提出了一种在检测到脉冲机动后进行协方差膨胀的跟踪方法,膨胀程度通过IMM算法确定,实现了对机动目标的实时跟踪,获得了与离线初始轨道确定相近的估计性能。许登荣等[23]针对传统IMM算法在模型集设计和转移概率方面的不足,采用强跟踪修正输入估计模型和匀速运动模型来构建模型集,并通过模型似然函数值对转移概率进行实时修正,提高了模型切换速度和跟踪精度。在此基础上,尹聚祺等[24]提出一种改进自适应模型转移概率计算方法,克服了模型似然函数比在机动时刻出现奇异的问题,并进一步在量测方程中引入速度测量,提高了跟踪精度。Ebrahimi等[25]提出了一种基于二阶马尔可夫模型的IMM算法,能够更精确的描述系统行为,取得了比一阶方法更好的跟踪效果。

以上研究均假设目标机动模式为脉冲机动,对于有限推力机动的场景,任家栋等[26]提出一种自适应变维两段状态估计法,该方法基于目标机动检测信息修正偏差滤波器的观测矩阵,以匹配目标机动加速度至滤波新息的转移矩阵演变特性,提高了算法的响应速度。马广富等[27]针对IMM算法模型集先验信息不准确影响导航精度的问题,引入自适应参数估计器在实际模型参数附近逼近真实的模型参数,提高了算法的鲁棒性和抗干扰能力。Yin等[28]将残差归一化强跟踪算法与当前统计Jerk模型相结合,提出一种自适应估计方法,解决了传统方法在目标机动的开始和结时刻估计精度低和不稳定的问题,可实现对不同机动水平目标的有效跟踪。

随着技术的不断发展,目前越来越多的GEO卫星配置了混合推进系统,如俄罗斯的Express通信卫星、中国的“实践-20”等[29-30],同时具备脉冲机动和有限推力机动两种机动模式,而已有的研究工作多针对目标机动模式仅为其中一种的场景,对同时存在两种机动模式的情况考虑较少。针对上述实际需求,本文研究了一种适用于混合推力机动目标跟踪的自适应IMM算法。首先,考虑目标无机动、脉冲机动和有限推力机动三种运动状态,建立了混合推力机动模式下的交互模型集;然后,针对IMM算法存在模型间交互概率近似和跟踪响应速度慢的问题,提出基于自适应模型转移概率的IMM算法;最后,通过数值仿真对所提算法的性能进行校验,分析本文所提跟踪算法的有效性。

1 混合推力机动模型集设计

IMM算法的一个关键步骤是交互模型集的设计。一个理想的模型集应能全面覆盖目标实际可能出现的运行状态,从这一角度出发模型集的规模应尽可能大。然而,过大的模型集会造成模型间的无效竞争以及计算量的急剧增大,导致算法跟踪性能下降。因此,为了更加准确的描述机动目标状态,且不过度增加计算成本,本节从GEO卫星典型的混合推力配置出发,构建混合推力下的交互模型集。

1.1 GEO卫星机动特性

GEO卫星配置的推进器从技术层面大致可分为化学推进和电推进两类。化学推进是目前应用最广泛、技术最成熟的推进方式,具有推力大、响应快、冲量控制精度高等特点,但比冲低,需要携带大量燃料。中国常见的化学推进器有1 N、5 N、10 N、20 N以及490 N推力器,如东方红4号平台的推进系统,由1台490 N和14～16台10 N化学推进器构成。其中,490 N推进器用于远地点轨道转移,10 N推进器用于卫星位置保持机动、卫星姿态控制等。电推进是近年来国内外重点发展的推进技术,具有比冲高、能耗低、寿命长等特点,但推力较小,输出推力幅值通常为毫牛级,远小于化学推进器,如“实践-20”(东方红五号平台)配置的LIPS-300电推进系统有两个不同档位,具备100 mN(高比冲模式)/200 mN(大推力模式)双模式输出,比冲可达到3500 s以上,设计寿命超过20000 h,可满足高轨卫星15年以上寿命需求,任务能力由南北位置保持单项任务拓展到变轨、位置保持和动量轮卸载等多项任务。其中,在进行轨道转移机动时电推进器需要以大推力模式工作,在进行位置保持机动时需要以高比冲模式工作。

由于工作原理不同,化学推进和电推进呈现出不同的机动特性。以位置保持机动为例,受摄动力的影响,GEO卫星自由漂飞过程中会逐渐偏离定点位置,需定期进行东西和南北向机动来维持轨位,以避免邻近卫星的信号干扰甚至碰撞,保证自身的安全和工作性能。特别是南北向位置保持,每年需提供约50 m/s的速度增量,差不多是东西向的10倍。采用化学推进时,通常需每两周点火一次,每次持续数十分钟,提供约2 m/s的速度增量,由于与轨道周期相比推力输出时间很短,故可视为脉冲机动。而采用电推进时,由于推力较小,需要采取一种预防式的运行策略,每天开机数小时,来达到与化学推进相同的效果,此时脉冲机动假设便不再适用,通常称为有限推力或连续小推力。上述特性在轨道转移机动过程中表现更为明显。

由于推力大小的不同直接反应为加速度的不同,故本文直接以目标机动加速度来表征目标的机动特性。考虑GEO卫星质量通常较大,在2000～5000 kg不等,根据牛顿第二定律给出目标机动类型、特性和相应配置,如表1所示。

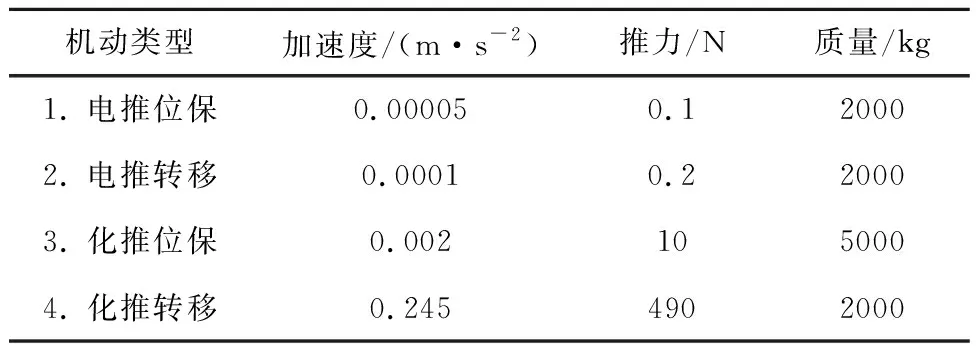
表1 目标机动特性Table 1 Target maneuverability

化/电混合推进系统将化学和电推进两种方式结合,在降低燃料消耗的同时,减少了轨道机动时间,拓宽了GEO任务设计的可行空间,提高了应对意外情况的能力。相应地,其机动特性也更加多样,可出现表1所示机动类型中的任意形式。

1.2 相对运动状态方程

结合脉冲机动和有限推力机动不同的机动特性对两星相对运动进行建模。卫星相对运动通常在轨道坐标系中研究,以目标星质心为原点建立VVLH(vehicle velocity local horizontal)坐标系,其中X轴指向目标星速度方向,Z轴指向地球质心,Y轴满足右手定则,如图1所示。

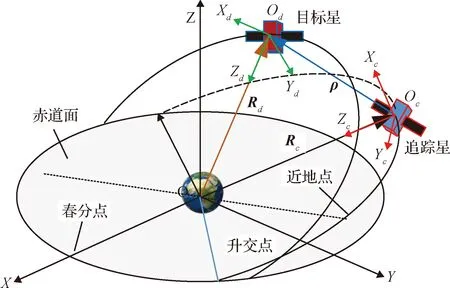
图1 相对运动示意图Fig.1 Relative motion diagram

由于GEO卫星轨道偏心率较小,可视为近圆轨道,且在机动目标跟踪场景中两星相对距离较近,根据苛式定律,可得GEO两星相对运动的数学描述,即C-W方程,有

(1)

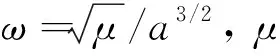
若不考虑推力作用,式(1)的解可写为

X1(t)=Φ1(t,t0)X1(t0)+G1W1(t)

(2)

式中:Φ1(t,t0)为状态转移矩阵;G1为噪声驱动矩阵,且有

(3)

其中,

Φvr(t,t0)=

式中:τ=t-t0。

式(2)离散化后可得

X1(k+1)=Φ1(k)X1(k)+G1w1(k)

(4)

式(2)给出了目标无机动时的相对运动状态方程,那么当目标执行脉冲机动时,其状态方程为

X2(t)=Φ1(t,t0)X2(t0)+BU(t)+G2w2(t)

(5)

将控制输入纳入到状态变量中,相对运动状态变为由位置速度以及加速度组成的增广相对运动状态,即X2=[x,y,z,vx,vy,vz,ux,uy,uz]T,那么式(5)可写为增广状态方程的形式

X2(t)=Φ2(t,t0)X2(t0)+G2W2(t)

(6)

其中,

(7)

对式(6)离散化后有

X2(k+1)=Φ2(k)X2(k)+G2W2(k)

(8)

式中:U(k)=δt,kU;U=[ux,uy,uz]T为脉冲推力加速度,为克罗内克函数,当t=k时,δt,k=1,其余时刻δt,k=0。

类似,当目标执行有限推力机动时,其离散化的增广状态方程可写为

X3(k+1)=Φ3(k)X3(k)+G3W3(k)

(9)

式中:Φ3与Φ2的区别在于,有限推力加速度U(k)=U。

式(4)、式(8)、式(9)共同组成了混合推力机动下的交互模型集的状态方程。与已有研究仅对无机动和脉冲或有限推力机动进行建模不同,本文所建立的混合推力机动模型包含了无机动、脉冲机动和有限推力机动三种状态,覆盖了卫星可能的机动形式。需要注意的是,模型1的状态变量中不包含加速度项,使得无机动情况下相对运动模型为6维,而模型2和模型3的状态变量均包含加速度项,模型规模增加到9维。

1.3 相对运动量测方程

追踪星利用自身携带的雷达设备实现对目标星的状态测量,量测量为相对距离ρ、俯仰角α和偏航角β,可建立天基量测方程为

Z(t)=h(X)+v(X)

(10)

式中:v为量测噪声,且有

(11)

对于无机动情况,量测方程的雅克比矩阵为

(12)

式中各元素为

H2,3=[H1,03×3]

(13)

2 IMM算法原理及其改进

2.1 IMM算法步骤

标准IMM算法包含模型输入交互、模型估计、模型交互概率更新、状态综合输出4个模块。由于模型集中有三个模型,故滤波器采用三个EKF滤波器,记为EKFi(i=1,2,3)。下面以k-1(k=1,2,…,n)时刻到k时刻的算法运行过程为例给出IMM算法的步骤。

1)模型输入交互

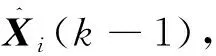
(14)

式中:mi|j(k-1)为k-1时刻从模型i到模型j的预测模型交互概率;mi(k-1)为k-1时刻模型i的发生概率;γij表示从模型i到模型j模型交互概率,且有

(15)

2)模型估计

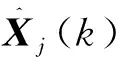
首先得到状态和误差协方差一步预测,

(16)

接着计算新息和新息协方差,

(17)

然后计算滤波增益和状态估计及协方差值,

(18)

3)模型交互概率更新

假设模型j的新息vj(k)服从高斯分布,那么新息似然函数Λj(k)和模型发生概率mj(k)的更新公式为

(19)

(20)

4)状态综合输出

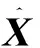
(21)

2.2 IMM算法模型交互概率分析

在面向GEO卫星的跟踪任务中,如果目标机动能力弱、机动范围小,比如进行有限推力机动时,那么可采用区分较小的模型集设计方法,以便获得更好的稳态跟踪性能,此时量测噪声通常远大于过程噪声,那么在估计过程中,过程噪声所包含的目标运动特性完全被量测噪声所覆盖,使得新息噪声特性仅由后者决定。根据式(17)可得如下关系

(22)

使得各模型新息似然函数取值近似相等,有

Λ1(k)≈Λ2(k)≈Λ3(k)⟹m1(k)≈

m2(k)≈m2(k)≈1/3

(23)

在这种情况下,各子模型的交互概率趋于一致,导致跟踪结果实际上是对各模型估计结果取平均,这与IMM算法优势互补的初衷背道而驰。

2.3 自适应模型交互概率设计

针对上述问题,本文对模型概率计算方法进行改进,使得在目标处于无机动状态时,模型1的概率提高,在目标处于机动状态时,模型2或3的概率提高。

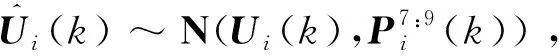
可定义函数

(24)

显然,当目标无机动时,λi(k)约为1,当目标机动时,λi(k)为小于1的一个较小值,且目标机动加速度越大,λi(k)的数值衰减越快。根据这一规律,采用缩放变换的思想设计自适应修正函数κ,有

κi(k)=r1r2(1-λi(k))

(25)

式中:r1,r2为调节参数,用于调整修正函数κ的调节速度。

对于式(25),当目标无机动时,κi(k)为1,当目标执行机动时,κi(k)的值应迅速增大,根据调试经验,可取r1=10,r2=6。

修正后的模型概率更新公式为:

(26)

改进后的算法应更能贴合目标机动特性的变化。结合表1中给出的GEO卫星典型机动特性,可以做出如下判断:若加速度估计状态小于0.00005 m/s2,可认为目标无机动或者微小机动,此时应提高模型1所占比重,最终的估计结果接近模型1;若加速度估计状态大于0.00005 m/s2而小于0.002 m/s2,此时要提高模型3所占比重;若加速度估计状态大于0.002 m/s2,可认为目标机动较为剧烈,应以模型2为主,最终的估计结果接近模型2。

3 仿真校验

为验证本文所提算法的有效性,采用GEO卫星位置保持和轨道转移两种典型的机动工况进行仿真,并进行性能比较。

假设追踪星运行在GEO上,采用雷达对目标星进行测量,实时获得目标的相对距离、俯仰角和偏航角参数,量测噪声根据某实际系统取为[(0.0005ρ)2m2, (0.01/57.3)2rad2, (0.01/57.3)2rad2],两星初始相对距离为20 km,初始相对状态为[20 km,0,0,0,0.1 m/s,0.1 m/s]T,初始过程噪声矩阵为diag(10-4,10-4,10-4,10-8,10-8,10-8),初始模型交互矩阵对角线元素分别为0.9,0.05,0.05。

目标星在自由漂飞一段时间后执行未知机动。需要指出的是,在通常情况下,脉冲推力机动在前,有限推力机动在后,这是因为若先进行有限推力机动后再进行脉冲推力机动可能会对卫星造成瞬时冲击影响,严重时甚至对太阳翼带来损伤。

1)工况一:假设追踪星与目标星均处于自由漂飞状态;无控运行4000 s后,目标星执行南北向的位置保持控制,首先启动化学推进器,径向推力大小为10 N,控制加速度为0.002 m/s2,执行时间持续500 s后停止,在6000 s启动电推进器,径向推力大小为100 mN,控制加速度为0.00005 m/s2,持续运行至20000 s,具体如图2所示。

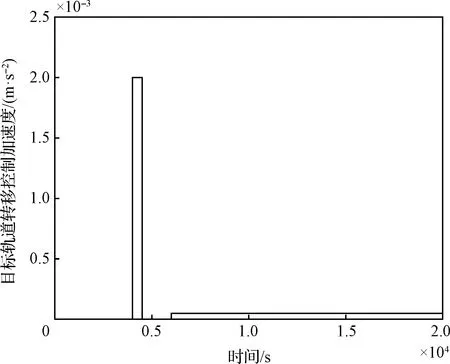
图2 目标位置保持控制标称推力加速度Fig.2 Target position holding control nominal thrust acceleration

分别采用“经典IMM算法”“经典IMM+混合模型算法”“混合模型+自适应模型交互概率算法”(本文)进行机动目标跟踪估计,如图3所示。

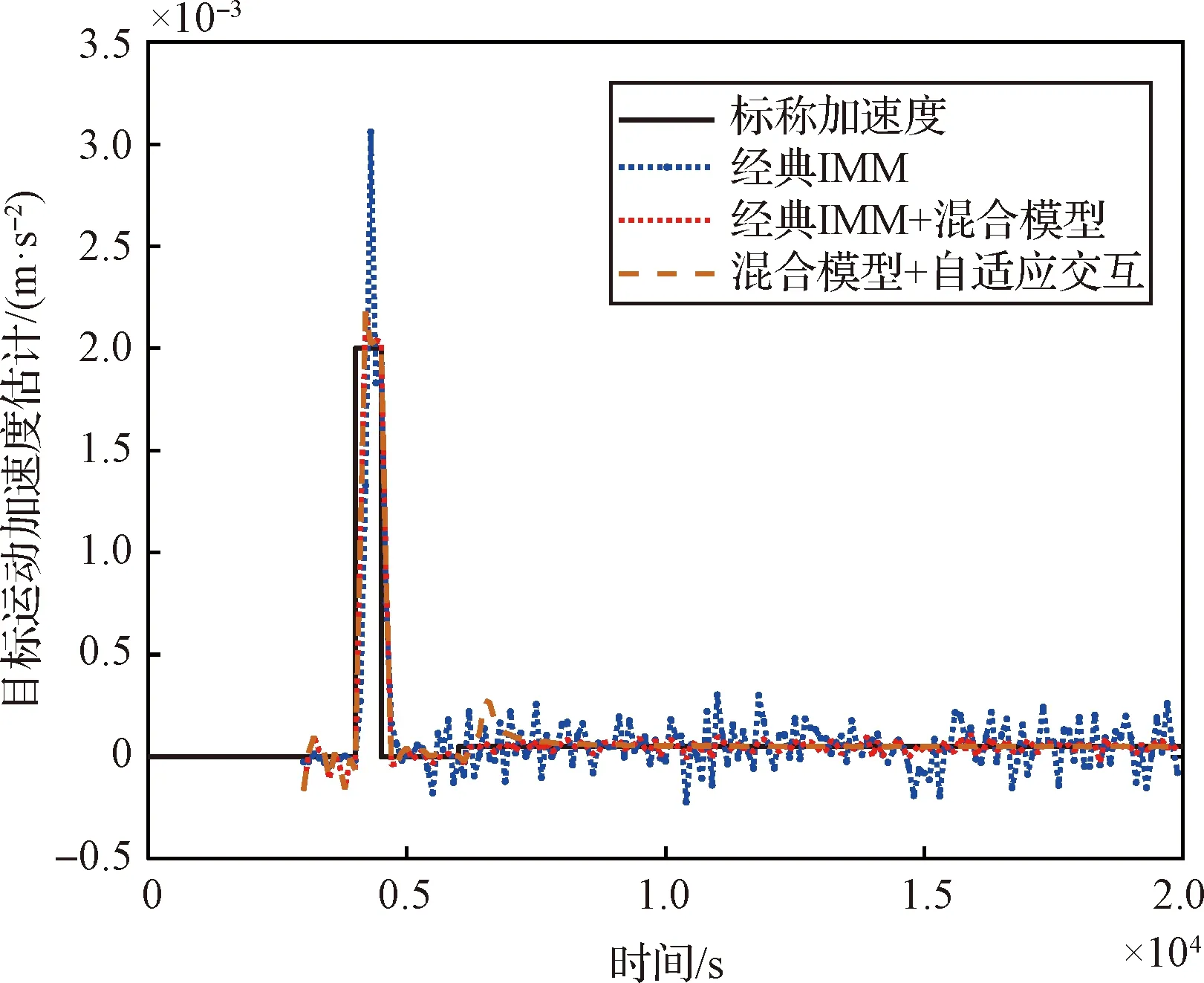
图3 目标位置保持控制加速度估计性能比较Fig.3 Comparison of target position holding control acceleration estimation performance

由图3可以看出,在目标进行脉冲机动时,三种方法均能够对其进行跟踪,但跟踪性能有明显区别。脉冲机动部分的跟踪曲线如图4所示。

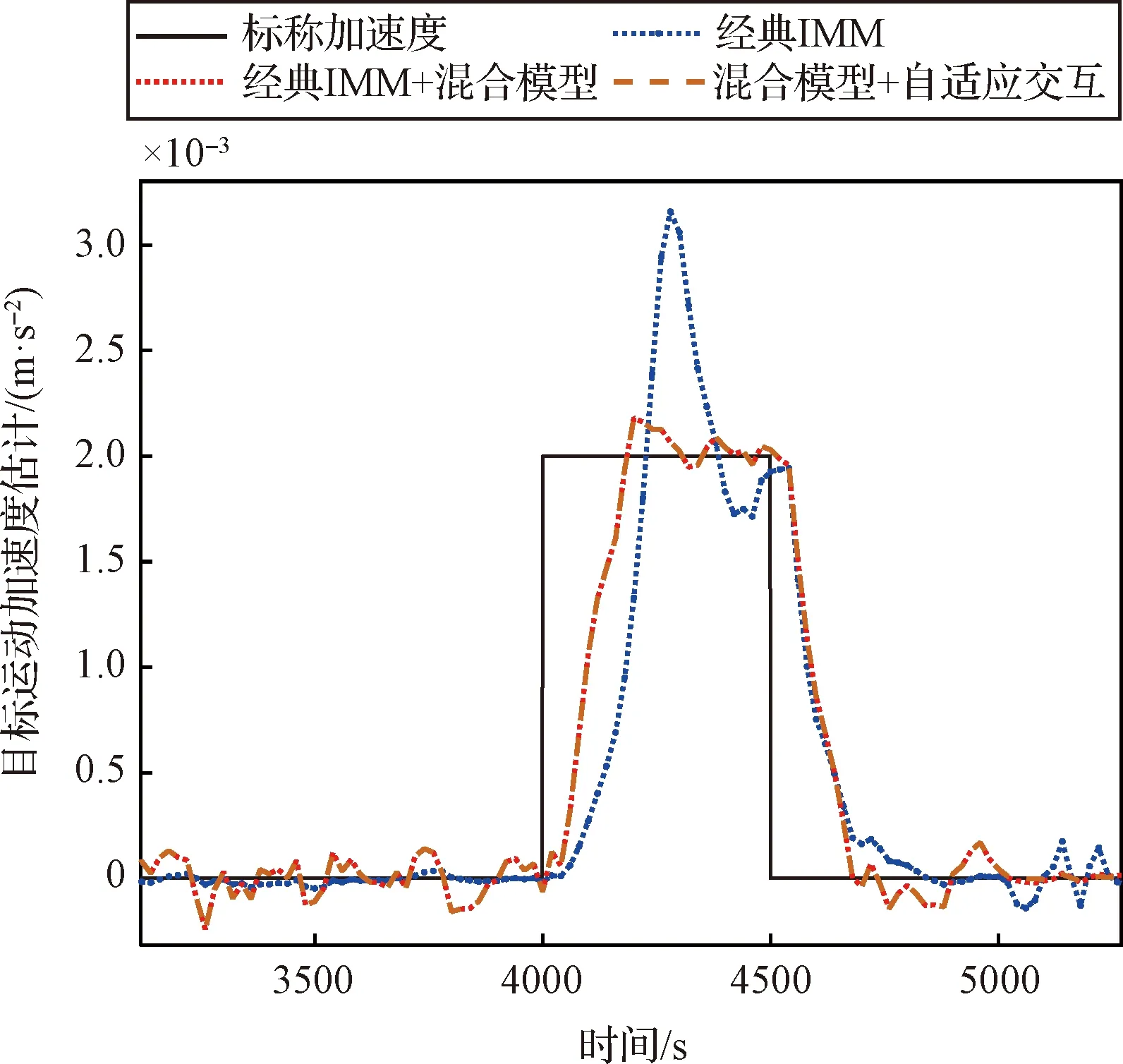
图4 工况一目标脉冲机动跟踪性能对比Fig.4 Target pulse maneuver tracking performance comparison of Scenario 1

“经典IMM”算法跟踪过渡时间长,持续约300 s,且滤波峰值较大,在需要较短时间的脉冲机动跟踪情况下很难得到准确的估计结果。引入混合模型后,收敛速度和收敛精度有了明显的改善,经过约200 s后即可较为稳定的估计出目标机动加速度。

图3有限推力机动跟踪部分如图5所示。由图5可以看出,对于有限推力机动跟踪,经典IMM方法完全失效。在增加了混合模型后,估计效果有了明显改善,但依然无法稳定收敛到标称加速度。本节所提“混合模型+自适应模型交互概率算法”具有最好的跟踪性能,能够快速准确地估计出目标有限推力加速度,且跟踪精度较高。

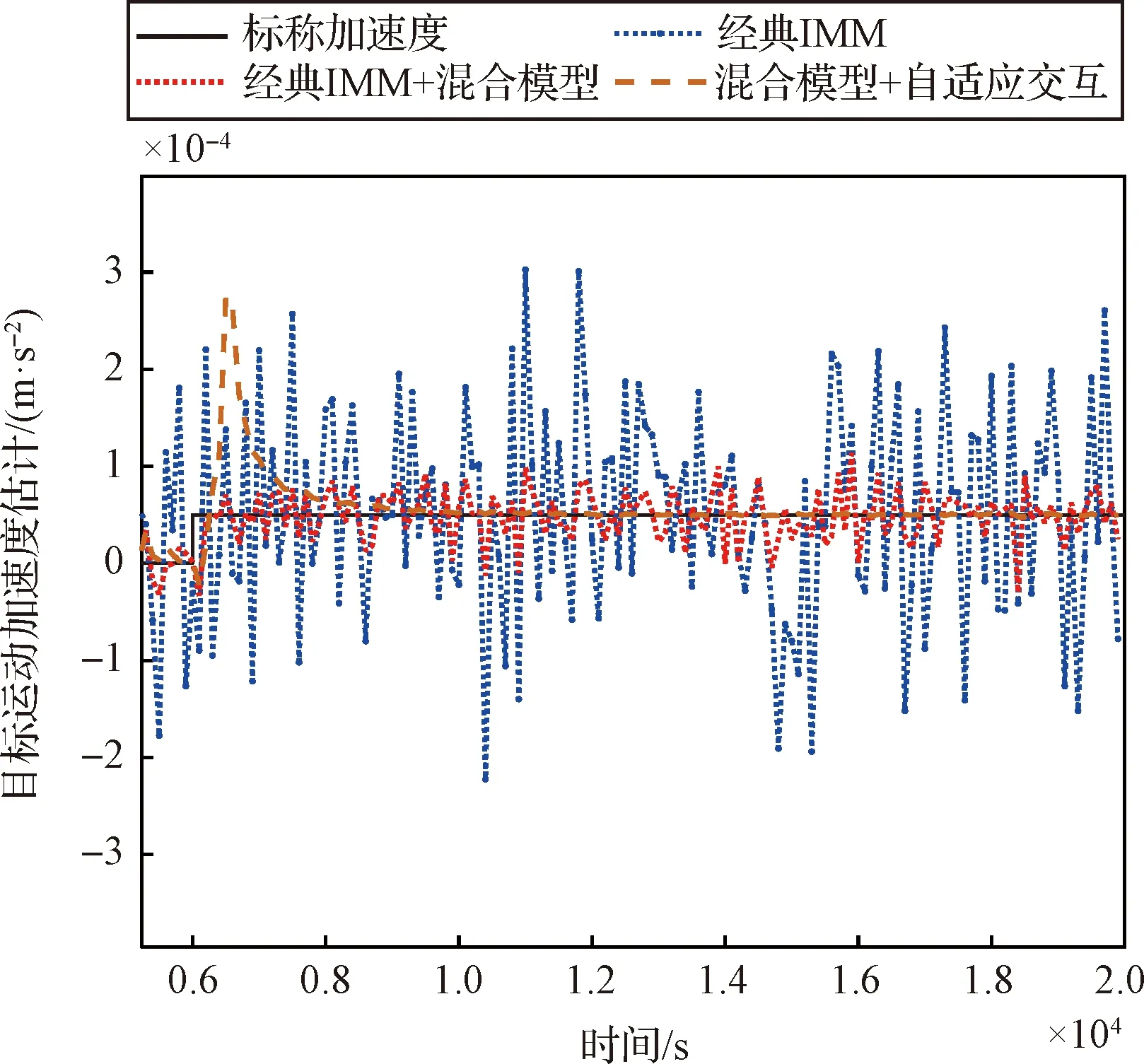
图5 工况一目标有限推力机动跟踪性能对比Fig.5 Target limited thrust maneuver tracking performance comparison of Scenario 1

再进一步,给出位置和速度误差仿真曲线,如图6和图7所示。

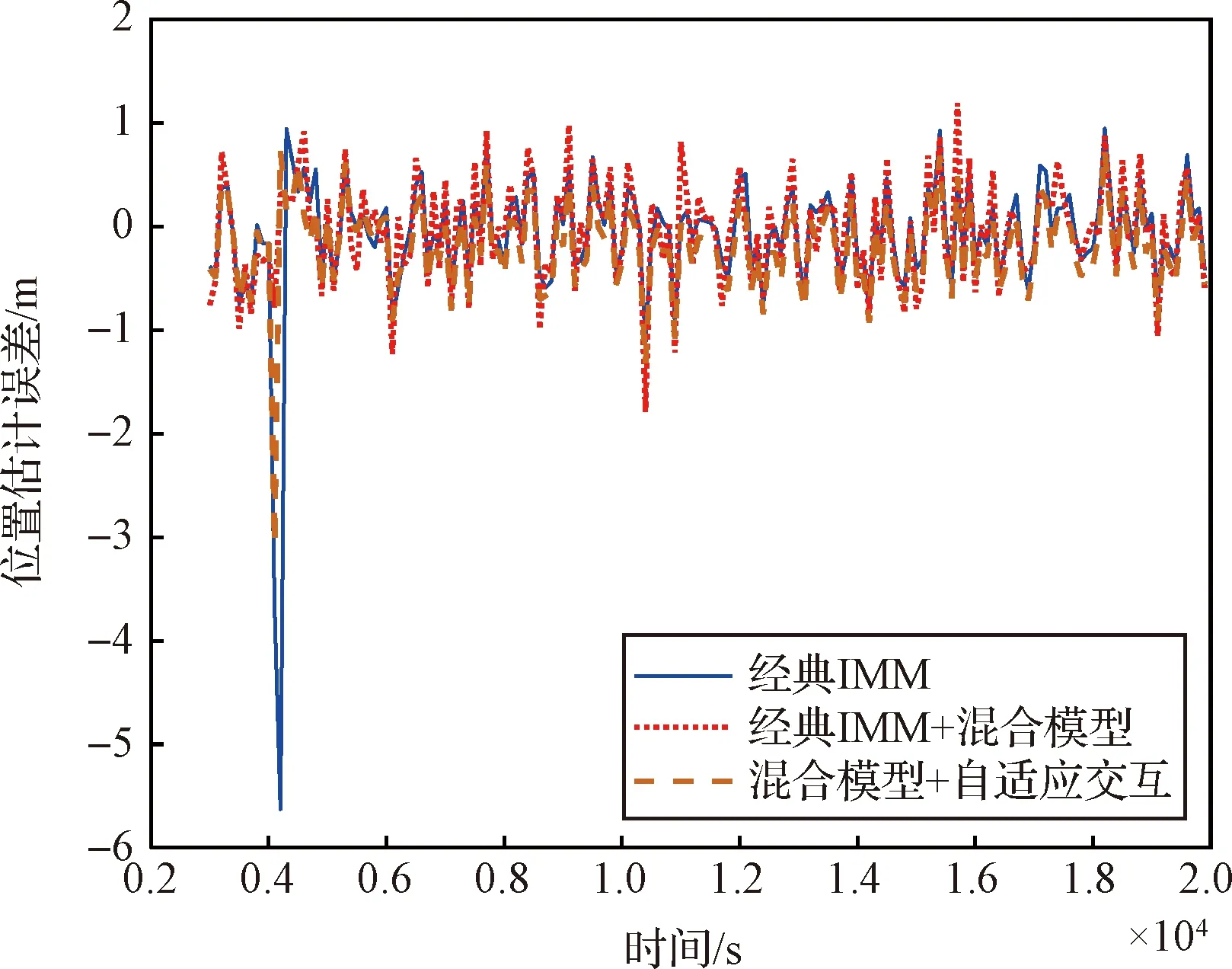
图6 工况一位置误差曲线Fig.6 Position error of Scenario 1

可以看出,三种方法中本节所提算法具有最好的位置和速度估计性能。实际上,目标执行位置保持控制期间,脉冲和有限推力加速度均比较小,位置和速度的变化较慢,相应的过程噪声和量测噪声也较小,因此在误差量级上没有特别巨大的差距。经典IMM算法在整个跟踪过程中对所有模型平均分配,在脉冲机动期间具有一定的跟踪能力,但无法匹配有限推力机动情况,使得在目标执行有限推力机动时跟踪失效。在引入了混合模型后,虽然改善了脉冲机动的估计效果,但在目标执行有限推力机动时没有能够切换至对应的模型,在无机动模型和有限推力模型间取了折衷,跟踪效果依然不理想。而本文所提算法能够在目标执行机动后迅速切换至匹配模型,说明了改进设计的有效性。

2)工况二:假设追踪星与目标星自由漂浮运行4000 s后,目标星执行轨道转移机动,首先启动化学推进器,径向推力大小为490 N,控制加速度为0.245 m/s2,执行时间持续500 s后停止,在6000 s启动电推进器,径向推力大小为200 mN,输出加速度为0.0001 m/s2,持续运行至20000 s(实际要比这个时间长得多),具体有:

分别采用“经典IMM算法”“经典IMM+混合模型算法”“混合模型+自适应模型交互概率算法”进行机动目标跟踪,有

由图9可以看出,在目标执行脉冲机动时,三种方法均能够对其进行跟踪。脉冲机动部分的跟踪曲线如图10所示。

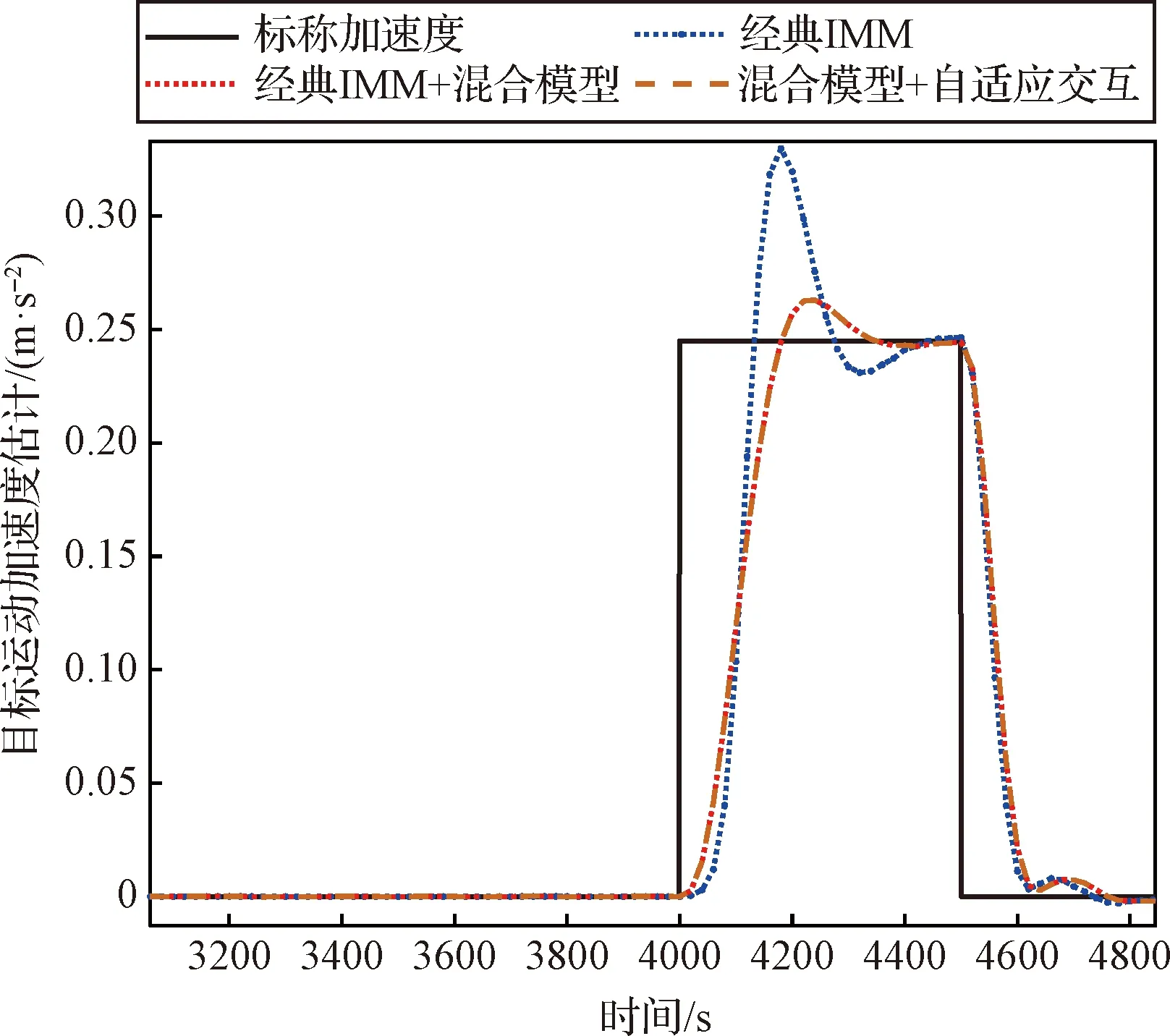
图10 工况二目标脉冲机动跟踪性能对比Fig.10 Comparison of target pulse maneuvering tracking performance of Scenario 2

在轨道转移机动条件下,三种算法的过渡时间均小于工况一。经典IMM算法的在目标机动期间并未完全收敛,很难得到准确的估计结果。其余两种结果在收敛精度和收敛速度方面均有较好表现。

图8有限推力机动部分如图11所示。

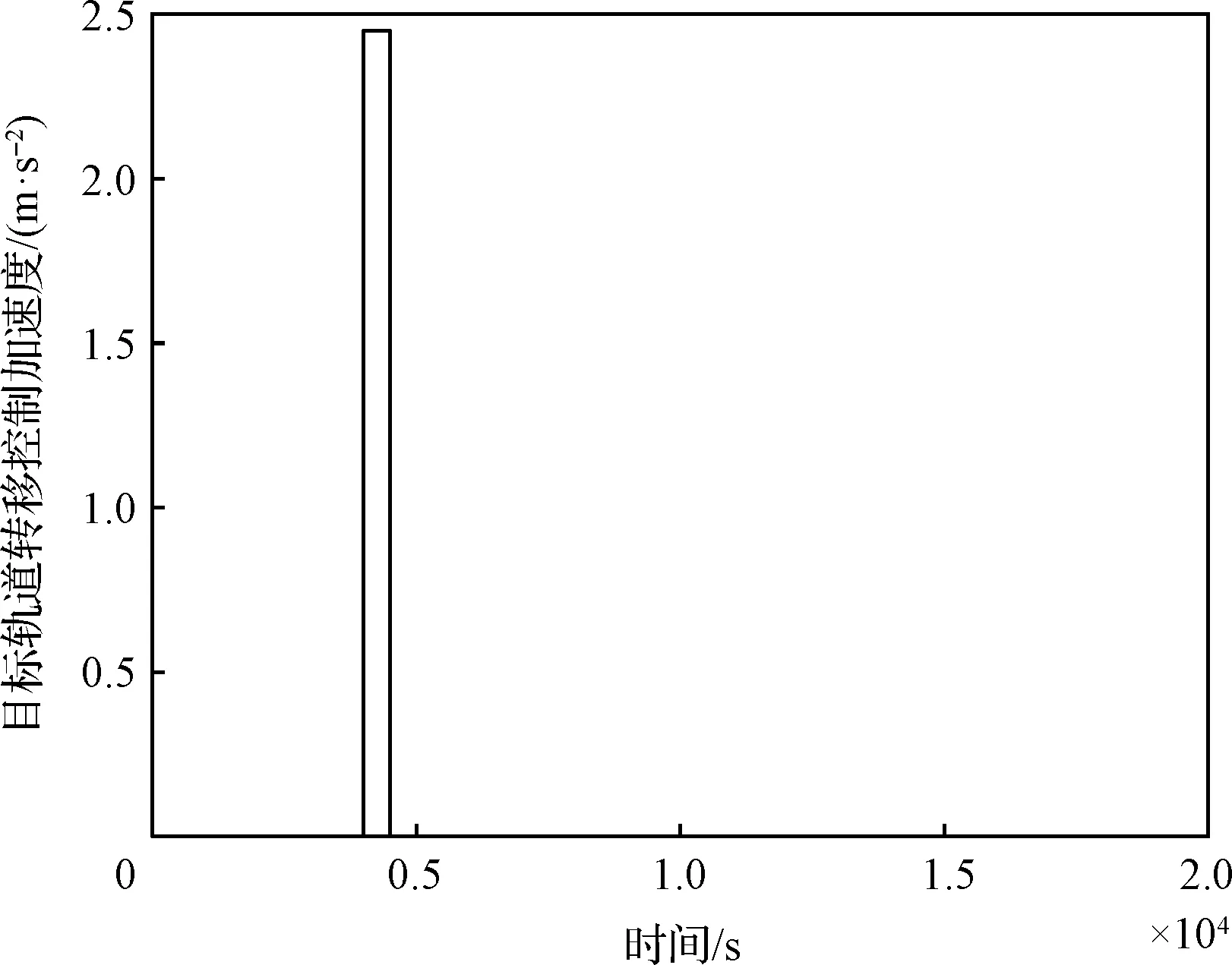
图8 目标轨道转移控制标称推力加速度Fig.8 Target orbit transfer control nominal thrust acceleration

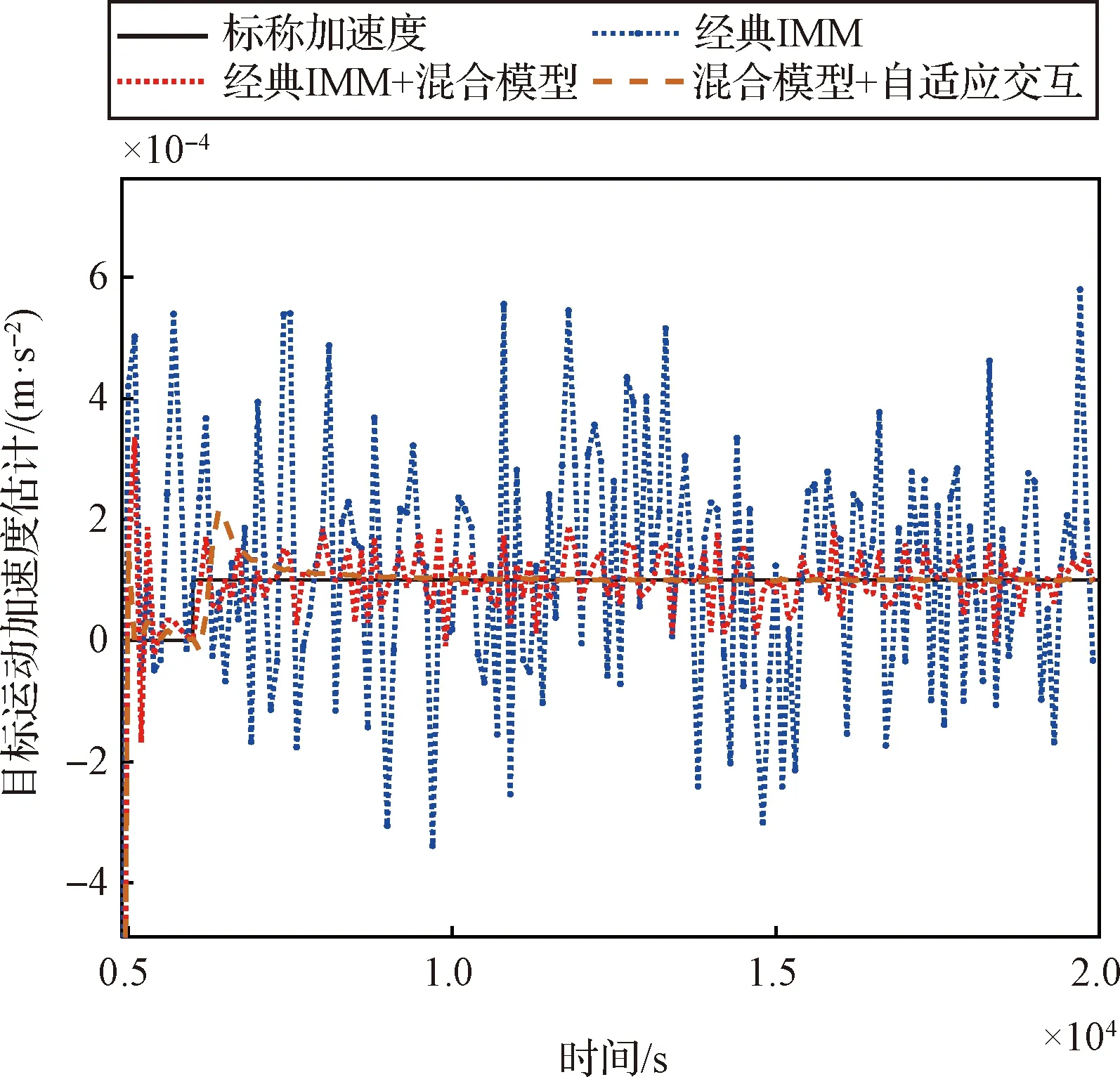
图11 工况二目标有限推力机动跟踪性能对比Fig.11 Comparison of target limited thrust maneuvering tracking performance of Scenario 2

可以看出,与工况一相同,对于工况二目标轨道转移机动条件下的有限推力机动跟踪,经典IMM方法完全失效。在增加了混合模型后,估计效果有较为明显改善,但依然无法稳定收敛。本文所提“混合模型+自适应模型交互概率算法”跟踪性能最好,在收敛速度和精度方面均有较好表现。

进一步地,给出位置和速度误差仿真曲线,如图12所示。

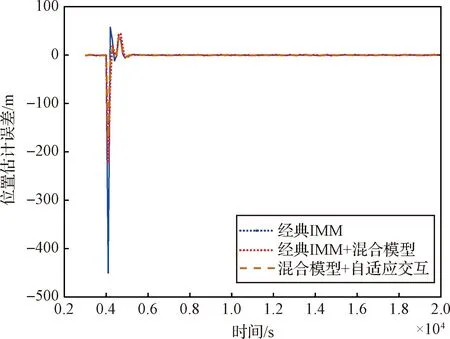
图12 工况二位置估计误差曲线Fig.12 Position estimation error of Scenario 2

由图12和图13可以看出,在三种方法的比对中,本文所提算法具有最好的位置和速度估计性能。由于轨道转移机动期间,脉冲和有限推力加速度与工况一相比均比较大,位置和速度的变化较快,因此估计误差明显比工况一要大。

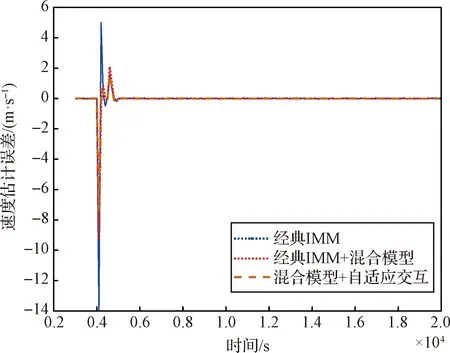
图13 工况二速度估计误差曲线Fig.13 Velocity estimation error of Scenario 2

与工况一类似,在引入了混合模型后,对脉冲机动的跟踪估计效果得到改善,但在目标执行有限推力机动时无法有效切换至对应的模型,跟踪效果依然不理想。本文所提算法在目标执行脉冲机动时,能够迅速切换至脉冲机动模型,并在后续执行有限推力机动时,能够及时切换,保证了跟踪速度和精度。

4 结 论

本文针对配置了混合推进系统的GEO机动目标跟踪问题,从交互模型集构建和模型交会概率设计两个方面出发,提出了基于改进IMM算法的GEO混合推力机动目标跟踪算法。首先,针对混合推进机动目标模型较难匹配的问题,给出了GEO目标典型机动特性,分别建立了无机动、脉冲机动和有限推力机动三种情况下的状态方程,覆盖了GEO卫星典型机动特性,构建了较为完善的交互模型集;其次,给出了IMM算法的基本步骤,针对IMM算法存在模型间交互概率近似的问题,提出一种基于加速度估计自适应修正的模型交互概率修正方法,增强了匹配模型的作用,充分发挥了模型交互的优势;面向目标进行位置保持机动和轨道转移机动的算例分析表明,本文所提算法是解决混合推力模式下的GEO机动目标跟踪问题的有效手段,在收敛速度和收敛精度等方面与传统方法相比有较大提高。根据对目标未知机动的估计结果,能够反推出目标执行机动的目的,为我方卫星的下一步动作提供参考。