一种航天器姿态控制与振动抑制的优化设计方法

胡雅博，耿云海，刘伟星

(哈尔滨工业大学航天学院卫星技术研究所，哈尔滨 150001)

0 引 言

大型空间结构将逐渐应用于不同的空间任务中,诸如空间太阳能电站、低成本空间航行以及在轨服务等[1-4]。随着航天器本身空间尺寸的增加,挠性成为控制系统设计中不可忽略的因素。为实现这类航天器的高精度姿态控制,必须同时考虑其振动抑制问题。

近些年来,不少专家学者对大型挠性航天器的姿态控制与振动抑制问题进行了深入研究。根据执行机构的安装形式,主要可分为集中式安装以及分布式安装两类情形。前者可通过诸如经典的输出成型方法[5]以及轨迹平滑[6-7]等方法消除或降低控制信号对于系统振动模态的激励,也可以通过合理设计控制律来同时实现姿态镇定及振动衰减的目标[8]。但由于这类方法通常没有特定的作动器专门进行振动抑制,其振动抑制能力相对较弱。

考虑执行机构分布式安装时,姿态控制与振动抑制可采用不同的执行机构,如采用飞轮进行姿态控制,而采用压电陶瓷进行振动抑制[9]。然而,受限于结构性能的约,压电陶瓷对幅值较小的振动比较有效,但无法提供较大的力矩来抑制振幅较大的振动。因此,D’Eleuterio等[10-11]提出了陀螺挠性体的概念,其主要思想是通过将角动量视为分布参数进行建模,进而使系统增加了旋性(gyricity)这一属性。陀螺挠性体的物理实现可以认为挠性体每个体元内都包含了一个角动量执行机构。这种配置可以使系统的自然频率、模态以及阻尼受控,无疑为挠性体姿态控制及形状控制提供了新的思路。随后,Damaren和D’Eleuterio研究了陀螺挠性体航天器的优化振动抑制方法[12],并给出了陀螺挠性体在振动抑制时的能观性和能控性分析[13]。

在上述的开拓性研究中,角动量的分布是连续的,即任取挠性结构的一部分,均有角动量含于其中。为了方便工程实践,Hu团队[14-18]详细研究了角动量离散分布的陀螺挠性体,即角动量交换执行机构只安装于挠性体部分特定位置的情形。文献[14,17]给出了角动量交换执行机构离散分布时陀螺挠性体的建模方法,并给出了模型线性化的方法。文献[15-16]采用了模态观测器及自适应控制方法对角动量离散分布的陀螺挠性体进行姿态控制及振动抑制。文献[18]提出了模态奇异性的概念,对安装于挠性体的单框架控制力矩陀螺(SGCMG)进行了模态奇异分析。此后,郭继唐及其团队[19-21]对执行机构SGCMG进行了深入研究,给出了两种陀螺挠性体的控制方法。文献[20]研究了一种模态力矩补偿器,在不使用模态观测器的情况下,可以由安装于挠性结构的SGCMG提供抵消振动方程干扰输入的力矩,并由另一组安装于中心刚体的SGCMG完成姿态控制。文献[21]则采用了同一组SGCMG进行姿态控制及振动抑制,实现了姿态控制及振动抑制的一体化设计。文章分析了SGCMG的零运动虽然无法提供姿态控制力矩,但可以有效提供振动抑制力矩。上述研究中均考虑了特定的执行机构配置[15-16,19-21],即采用CMGs进行振动抑制或姿态控制,且文献[20-21]为执行机构的操纵律设计方法。为得到不过度依赖特定执行机构的设计方法,考虑执行机构上层的控制方法设计是有意义的。

Hu团队[22-23]探索了不考虑特定执行机构配置的姿态控制及振动抑制方法。文献[22]给出了一种姿态控制与振动抑制解耦设计的方法,通过增加振动抑制力矩共面的约,可以实现振动抑制过程中不产生影响姿态控制的力矩,但其姿态控制仍需另外的执行机构。文献[23]研究了力矩分配与系统阻尼的关系,提出了一种可以在姿态控制过程中增加系统阻尼的力矩分配方法,采用同一组执行机构同时实现了姿态控制及振动抑制。上述方法实现了挠性航天器的姿态控制,并可以不同程度抑制系统的振动,但其设计较为保守,并未实现某种指标的优化。此外,文献[23]对控制器产生的期望力矩直接进行分配,鲁棒性较差。若控制器偶然产生错误的控制力矩,即使力矩分配过程准确执行,仍可能导致航天器失稳。本文明确将振动抑制能力描述为优化指标,而将姿态控制的稳定性与动态性能归纳为问题约,对控制律参数进行分配,而不直接对力矩进行分配。如此,只要满足约,系统即是稳定的,通过优化是为了选择更好的振动抑制参数。

本文研究对象为分布式安装了角动量交换执行机构的陀螺挠性体航天器。考虑执行机构安装节点有简单的计算能力并采用形式相同的控制律。为满足姿态控制的动态性能及稳态性能,不同执行机构安装节点处的控制律参数需满足一定的等式约。为实现较好的振动抑制效果,设计含有不同节点处振动状态及控制力矩的目标函数。通过求解上述关于不同节点控制律参数的优化问题,不同节点可获取所需控制律参数,从而计算输出控制力矩完成姿态控制及振动抑制目标。数值仿真校验了所述方法的有效性。

1 分布式执行机构的挠性航天器模型

1.1 动力学模型

本文考虑的挠性航天器模型如图1所示,图中Ai(i=1,…,n)表示角动量交换执行机构的安装节点,n为执行机构安装节点数量。

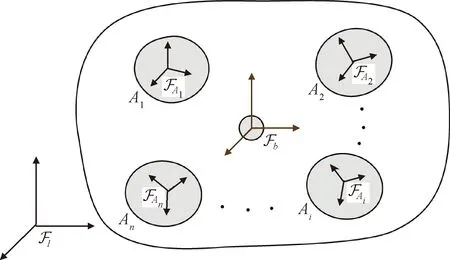
图1 陀螺挠性体航天器模型Fig.1 Gyroelastic spacecraft model

根据文献[17,21]可得上述陀螺挠性体动力学方程为:

(1)

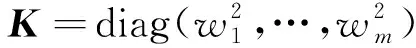
(2)

式中:Ti为执行机构安装节点Ai输出的控制力矩。可以看出,Ti不仅会对航天器姿态产生影响,同时也会通过转动模态矩阵Ri耦合到系统的振动方程中,进而影响系统的振动状态。这是陀螺挠性体与一般执行机构安装在中心刚体的航天器的最大差别,同时也是陀螺挠性体控制系统设计难点所在。

1.2 运动学模型

本文采用四元数描述航天器的姿态运动

(3)

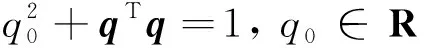
2 控制器设计

为了方便控制器设计及稳定性分析,首先将动力学模型整理为如下紧凑形式[21]

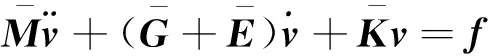
(4)

式中:

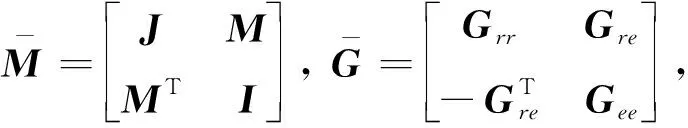
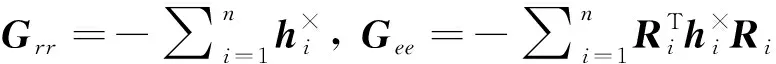
由于本文着重探讨如何将航天器的姿态控制和振动抑制问题转化为参数优化问题,所以此处选择形式较为简单的控制律进行阐述。考虑每个执行机构节点采用如下形式的控制律

Ti=-kpiq-kdiωi,i=1,…,n

(5)

式中:kpi>0,kdi>0为控制律增益。为分析控制律的稳定性,选择如下Lyapunov函数

(6)

式中暂时忽略了干扰力矩Td进行分析[20]。将式(6)沿系统(1)和(3)对时间求导可得

(7)

考虑控制律(5)及式(2),上式可整理为

(8)

(9)

式中:e=kpiqTqi/2且i>0。总可以找到n个i使得矩阵为正定矩阵,因此系统(1)和(3)在控制律(5)的作用下是一致最终有界的。易知,当干扰力矩Td有界时,重复上述推导过程可以证明系统依然是一致最终有界的。将控制律(5)代入式(2)可得

(10)

从上式可以大致看出控制律(5)不同部分的作用。等式右侧前两项为控制航天器姿态的PD控制律,最后一项为执行机构安装节点的振动阻尼。但由于Ti同时作用于系统的姿态运动方程及振动方程,kpi及kdi应根据某种标准进行选择设计,下节将探讨该问题的解决方案。

3 控制器参数确定

本节首先将待求解问题归纳为标准优化问题,给出了指标函数的设计方法以及待求参数的约。其次给出了优化问题的求解方法。

3.1 指标函数

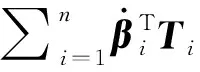
(11)

式中:Pi=diag(Pi1,Pi2,Pi3)为执行机构安装节点Ai处衡量系统振动状态的参数矩阵,Pij(j=1,2,3)将通过如下形式获取

(12)

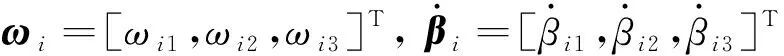
(13)

式中:a>0,b>0为设计参数。

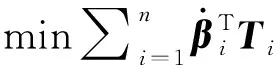
3.2 变量约

根据上节控制律设计需求,系统稳定的条件为kpi及kdi为正值。为使得系统满足特定的动态性能及稳态性能,需对kpi及kdi增加其他约。如

(14)

式中:kp>0及kd>0为根据特定需求给出的设计参数。由于式(14)包含了所有执行机构安装节点控制律的参数,因此其为关于kpi及kdi的全局约。可知,当节点采用其他形式的控制律时,同样可以给出如式(14)的约从而实现所需的姿态控制性能。

此外,执行机构的输出力矩应满足如下饱和约:

(15)

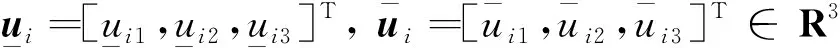
至此,可将挠性航天器姿态控制与振动抑制问题归纳为如下标准形式的优化问题

(16)

求解上述优化问题即可获得kpi及kdi,并且可以从优化振动抑制的角度解决挠性航天器姿态控制问题。

3.3 优化问题求解

从式(15)可以看出,关于kpi及kdi的饱和约是一个耦合的局部约。如果直接求解问题(16),耦合的约是较难处理的。为此,为每个节点Ai引入如下局部变量

yi=-kpiq-kdiωi

(17)

从而,优化问题(16)可写为如下等价形式

(18)

虽然引入的变量yi与节点Ai处的控制力矩Ti有相同的形式,但其意义是不同的。yi作为单独的变量参与优化问题的求解,即求解yi与kpi及kdi并没有先后顺序要求。而控制力矩Ti只有在确定kpi及kdi后才能计算求得。通过引入局部变量来处理局部耦合约的方法同样可以应用于其他形式的控制律,或其他优化问题中。

不难验证,问题(18)为凸优化问题,且满足Slater松弛条件,因此只要求得最优解即为全局最优解。

上述问题(18)的Lagrangian函数为

(19)

式中:

(20)

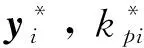
(21)

及互补松弛条件

(22)

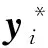
(23)

上式可以写为如下等价形式,对于j=1,2,3有

(24)

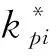
(25)

以及

(26)

综上,根据KKT条件,求解问题(18)等价于在满足问题可行性条件下求解如下方程组

(27)

至此,分布式执行机构的挠性航天器姿态控制及振动抑制问题通过优化方式求解完成。

4 仿真校验

本节采用类似文献[20-21]中仿真部分的陀螺挠性体模型进行仿真校验。模型为6 m×10 m厚度可忽略的不受限挠性体,其上均匀分布3×5组飞轮作为执行机构。通过有限元方法(FEM)可建立陀螺挠性体模型,模型参数如表1所示。依据惯性完备性准则考虑了如表所示的6阶模态。

表1 陀螺挠性体模型参数Table 1 Parameters of the gyroelastic spacecraft model

为了充分校验本文方法的有效性,考虑航天器进行一系列大角度姿态机动的工况。在160 s及300 s分别有165°的姿态机动任务,机动的欧拉轴在本体系的方向假设为[0.8729, -0.4364, 0.2182]T。对于控制律增益的约(14)取为kp=80,kd=600;式(12)中Sigmoid函数参数选择为a=1,b=300;执行机构力矩饱和限制选取为2 N·m。仿真结果如图2至图5所示。

图2和图3分别为航天器姿态机动的欧拉角及姿态角速度随时间变化的曲线,为了直观起见,将运动学方程使用的四元数通过3-2-1的方式转化为欧拉角进行绘图。通过调整kp和kd的值可以调整姿态控制的动态性能及稳态性能。可以看出,本文给出的控制器可以很好地完成航天器的姿态控制。最后一次姿态机动到进入稳态的时间约为240 s,姿态精度约为 0.07°,稳定度约为0.004(°)/s。图2和图3中稳态误差是由于仿真中考虑了干扰力矩。此外,若采用其他高级的控制律,应用本文给出的优化思路,对其相应的控制律参数进行分配,将会得到更好的动态性能及稳态性能。

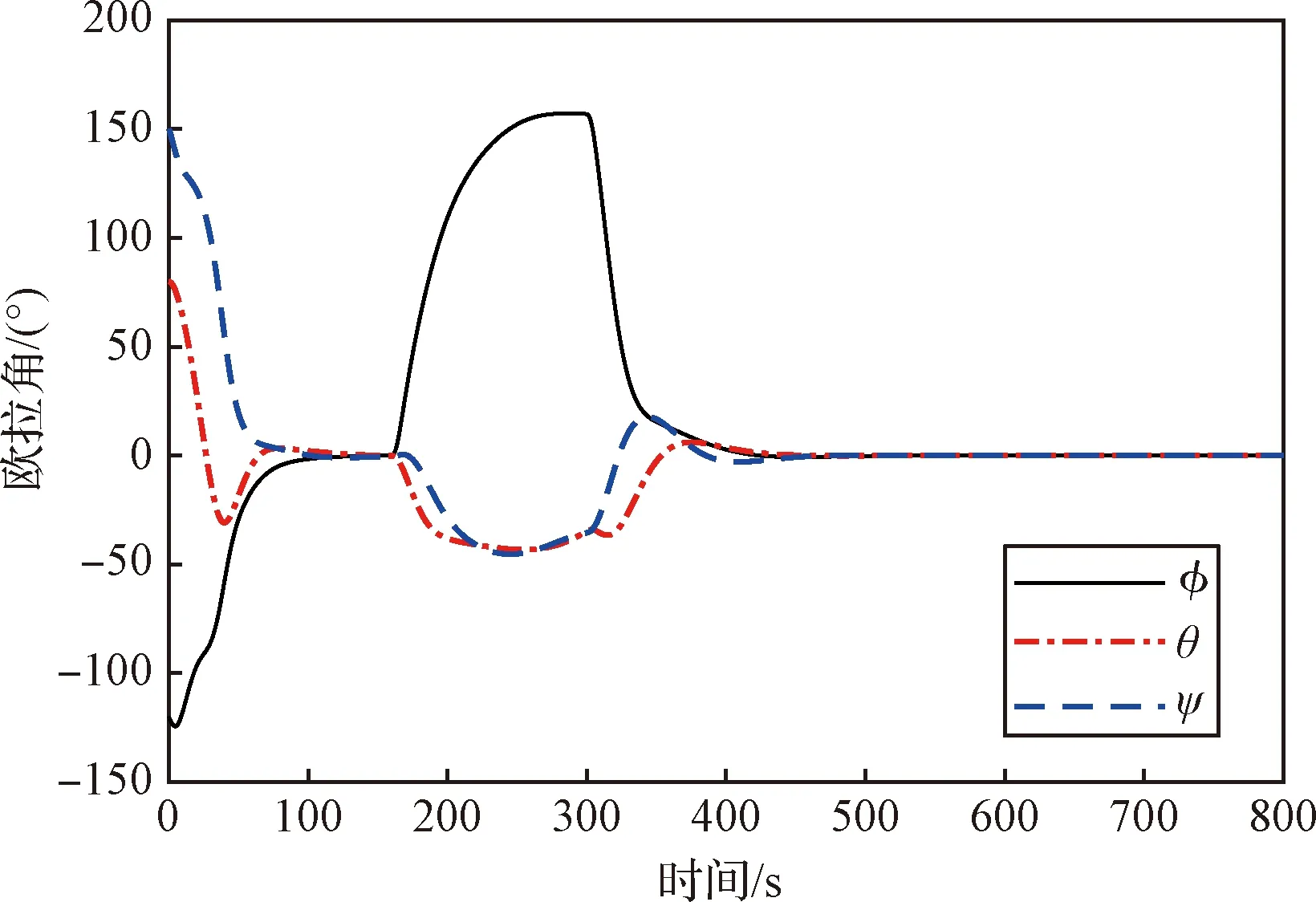
图2 欧拉角变化曲线Fig.2 Curves of Euler angles

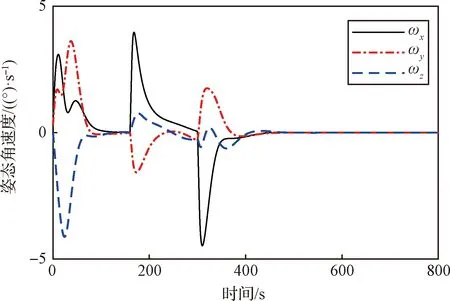
图3 姿态角速度变化曲线Fig.3 Curves of angular velocities

图4为模态坐标随时间变化的曲线。可以看出,在每次姿态机动开始时,系统振动比较大。结合图5可以看出在姿态机动开始时所需的控制力矩较大,且存在力矩突变,因而会激发系统的振动。通过本文给出的方法,系统振动可以很快衰减。

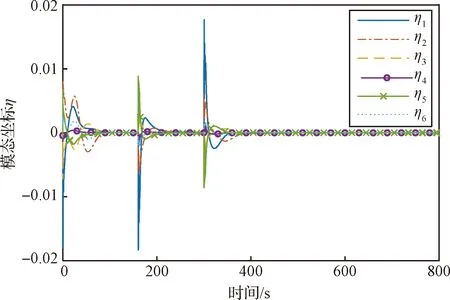
图4 模态坐标变化曲线Fig.4 Curves of modal coordinates

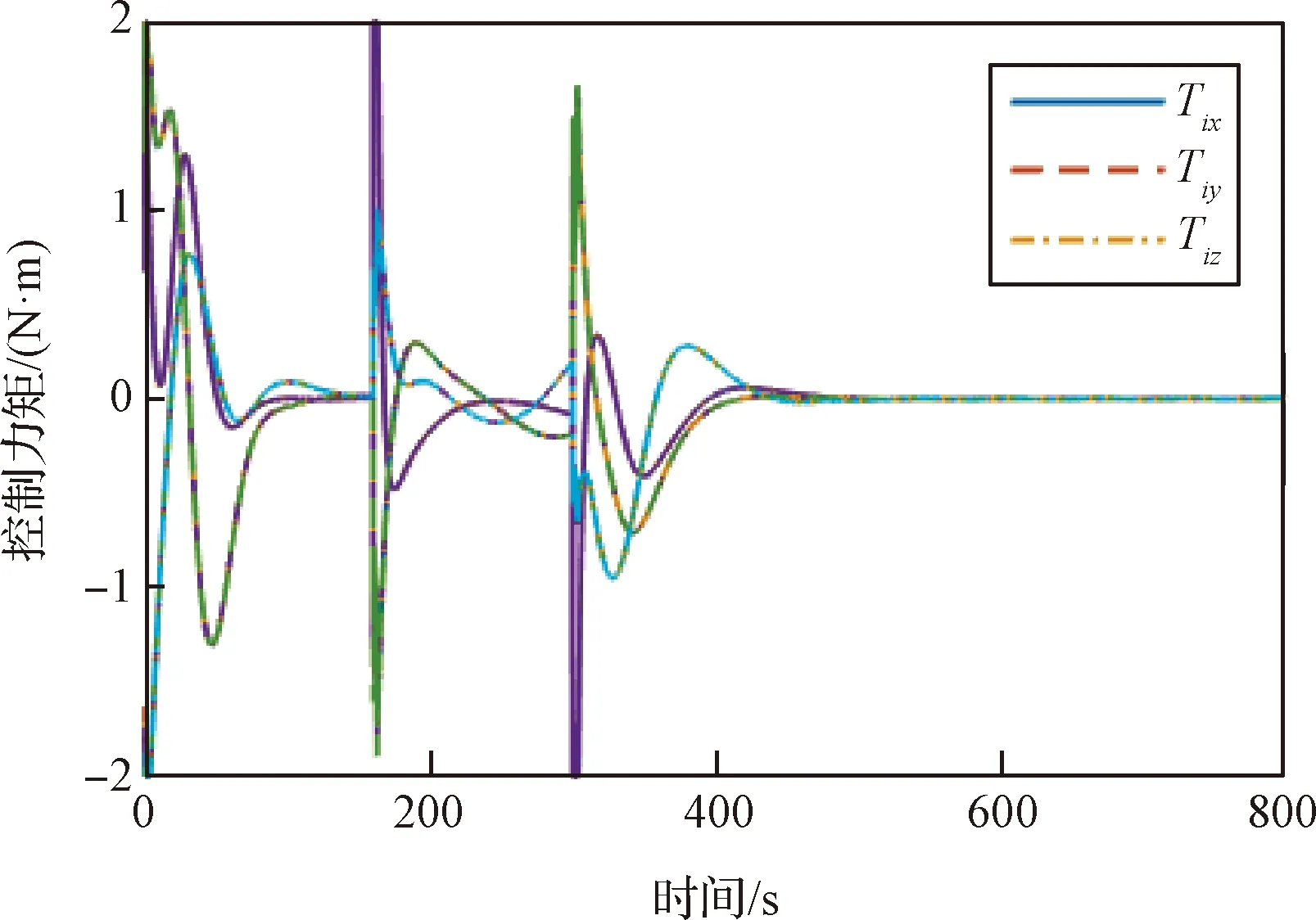
图5 执行机构输出力矩Fig.5 Torques generated by actuators

这里也可以看出陀螺挠性体跟采用其他作动器抑制振动的航天器特性的差别。由于安装于挠性部件的角动量交换执行机构输出力矩较大且直接作用于挠性体,其抑制振动的效果很好,这也表明除了进行振动抑制外,其还可以用于形状控制,即使得挠性体依据任务呈现特定的形状等。图5展示了所有执行机构的力矩输出情况,不同的线型表示了不同输出轴的输出力矩。从图中可以看出,航天器机动开始时,不同执行机构输出的力矩有较大差距,这表明优化方法为不同执行机构提供了其进行振动抑制的最优选择。当振动很快衰减后,不同执行机构输出力矩逐渐趋于一致,这表明振动较小时,控制律系数的选择对于振动本身的影响并不会太大。

为了分析本文给出方法的特点,此处给出了文献[23]方法的对比仿真。文献[23]通过力矩分配的方式进行振动抑制。为使得仿真对比具有“可比较性”,两方法应用的航天器模型参数一致,文献[23]方法中控制器参数的选取以“姿态角及姿态角速度动态性能与稳态性能与本文相应性能基本一致”为标准。在此基础上,比较模态坐标的收敛特性。根据以上阐述,文献[23] 的方法控制律参数选择为kp= 90,kd= 900;Sigmoid函数参数的选择为a= 1,b= 300。仿真结果如图6所示,为了行文简洁,此处略去了航天器姿态角及姿态角速度随时间变化的图像,其与图2及图3基本一致。

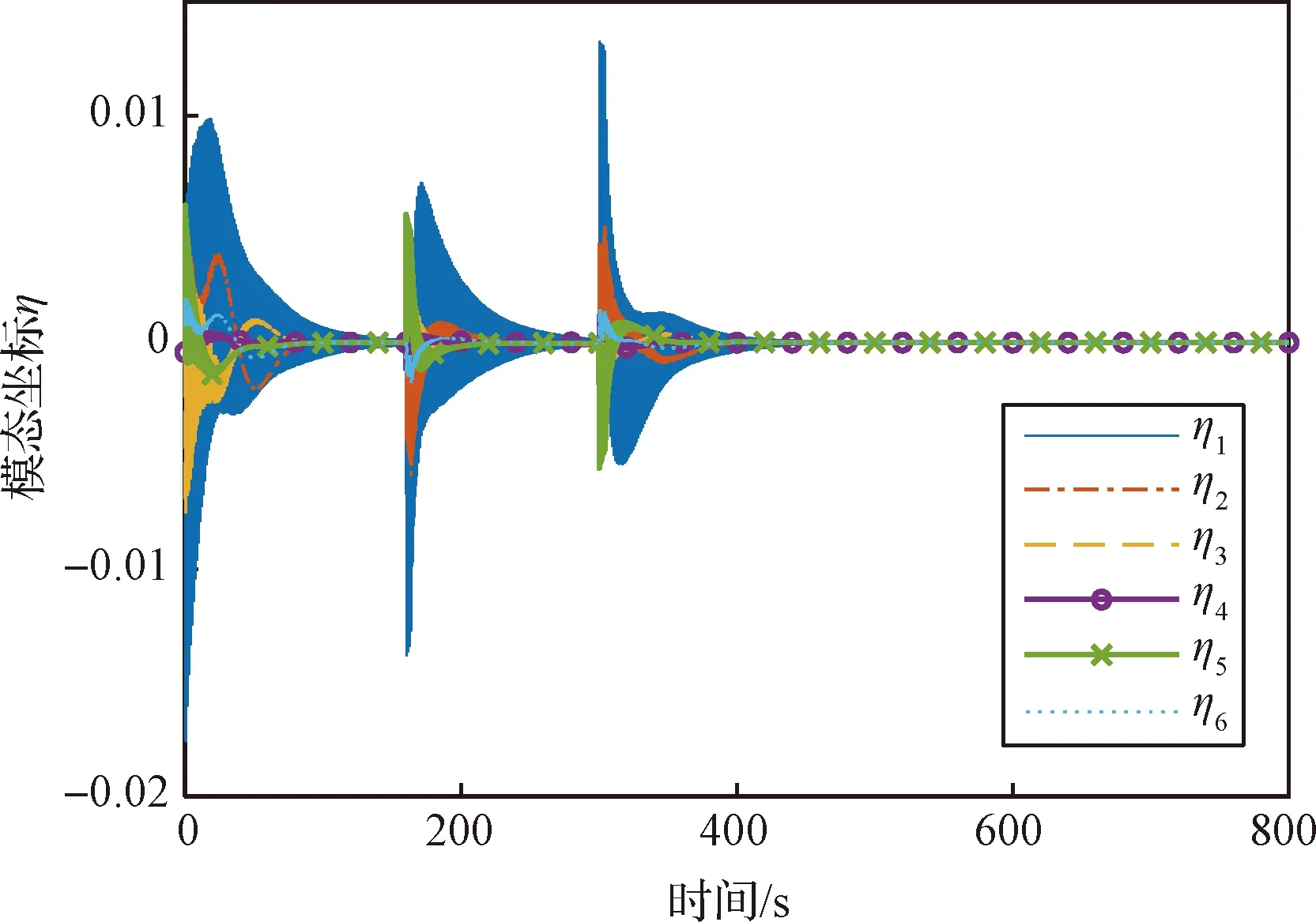
图6 文献[23]方法模态坐标变化曲线Fig.6 Time histories of modal coordinates by method in reference[23]

对比图4和图6可以看出,相比文献[23]给出的方法,本文给出的方法对于振动具有更快的衰减速率,优化效果明显。文献[23]的方法对于振动抑制的效果与其控制律参数选择甚至控制频率的选择并没有关系,其一方面不能处理执行机构力矩饱和,导致直接限幅会使得其控制效果大打折扣,尤其是在姿态控制的初期需要较大控制力矩的情形;另一方面,本文所述方法只要满足控制律参数的约,其自然而然就是具有振动抑制能力的,优化的结果只会使得振动抑制的效果更好,这是文献[23]方法所不具备的特性。

5 结 论

针对采用分布式角动量交换执行机构的挠性航天器,本文给出了一种基于优化的姿态控制与振动抑制方法。振动抑制的效果被明确描述为优化问题的指标函数,姿态控制的动态性能和稳态性能通过优化问题的等式约给出。使用Lyapunov方法证明了控制器的稳定性,当满足优化约时,可保证姿态控制的动态性能及稳态性能。通过求解KKT条件可以得到所述优化问题的全局最优解,该最优解具有优化指标意义下的最优振动抑制能力。对于采用分布式执行机构的大型系统,本文方法对其同时兼顾多个控制目标的控制系统设计具有较大参考价值。仿真表明,文中给出的方法能有效完成挠性航天器的姿态控制任务,并具有良好的振动抑制能力。相比于采用力矩分配进行振动抑制的方法,本文方法更能发挥执行机构的控制能力,并能更快衰减振动。