基于可观测性的序列图像自主导航观测时序规划方法

2023-04-15李嘉兴王大轶董天舒李茂登符方舟

宇航学报 2023年3期

李嘉兴，王大轶，董天舒，李茂登，徐超，符方舟

(1. 北京空间飞行器总体设计部，北京 100094；2. 北京控制工程研究所，北京 100094；3. 中山大学航空航天学院，深圳 518107)

0 引言

为了在科学探测区域定点着陆,并避开山丘和岩石等障碍,行星探测着陆器需要高精度的自主导航。惯性测量单元(Inertial measurement unit, IMU)是着陆器携带的一种基本自主导航设备,但导航初始误差、引力场模型误差和测量随机误差会导致IMU偏差随时间累积而逐渐增大[1]。因此,惯性导航往往需要与其他外部测量相结合以提高导航精度[2]。

为实现10～100 m级别的行星精确着陆,NASA和ESA从20世纪90年代末开始研究基于序列图像的导航技术[3]。在勇气号和机遇号火星着陆任务中,NASA使用降落图像运动估计系统(Descent image motion estimation system, DIMES)通过匹配三幅序列图像中的两个Harris特征来估计着陆器的水平速度[4]。JAXA的隼鸟1号使用视觉辅助导航系统通过将包含人造特征的照片传回地面来估计水平速度[5]。由于着陆器上计算和存储能力有限,大多数导航方案只获取少量的图像并从其中匹配少量的陆标,或者将图像发回地面进行处理。

基于序列图像和IMU组合的导航方法通常被称为视觉辅助惯性导航(Vision-aided inertial navigation, VAIN)。测量输入是序列图像中陆标相对着陆器的方向矢量,用于校正IMU偏差。但有些状态可能无法解算,即不可观测,因为在未知环境中观察到的陆标位置是未知的,或者观测次数不够。导航系统的可观测性正是用于确定状态是否可观测,近年来得到了广泛研究。在未知环境中,只观测未知陆标的情况下,Hesch等[6]分析了线性VAIN系统以及利用Lie导数分析了非线性VAIN系统[7]可观测性矩阵的右零空间,得到的可观测性分析结果表明位置和偏航角是不可观测的。在仅观测一个位置已知地标和多个未知地标的情况下,Martinelli[8]利用连续对称方法和Lie导数确定了非线性VAIN系统的偏航角不可观测。Feng等[9]针对线性VAIN设计了一个矩阵卡尔曼滤波器,并基于Lie导数推导出其可观测的条件是至少一个姿态转动并且至少观测三个不共线的陆标。现有针对VAIN可观测性的研究主要集中于判定哪些状态是可观测的以及可观测的条件,缺少针对保证可观测状态收敛的最少陆标个数和观测次数的研究,这是设计自主VAIN系统的重要边界条件。

为了降低着陆器上自主实现VAIN的计算负担,在不影响导航精度的条件下应尽量减少陆标个数和观测次数。因此,需要在着陆器上规划陆标的位置和观测时间,以从少量的观测信息中获得较高的导航精度。Sutherland等[10]分析了考虑陆标位置和测量角度误差共同作用下的位置解算误差界,以此来选择使位置解算误差最小的陆标进行观测。Xu等[11]提出了一种基于线性协方差技术的陆标选择算法,通过最小化所选状态参数沿标称轨迹在每个成像时间点上的不确定性来选择陆标。Zhang等[12]提出了一种基于熵的陆标选择方法,通过选择出最佳的新陆标并删去旧陆标,实现信息融合时熵减的最大化,从而降低信息融合时的计算负担。Lerner等[13]提出了在一种在已知环境中基于位姿不确定性的陆标质量度量方法,使用半定规划来最小化位姿误差的协方差,从而选择使导航精度最高的陆标。Yu等[14]利用可观测矩阵的条件数作为可观测度对陆标构型进行优化。朱圣英等[15]通过Fisher信息矩阵评价导航估计误差下限,对行星表面的地形特征点、直线和曲线进行优化选取。现有陆标观测规划方法主要集中于从空间的角度挑选位置最好的陆标,可用于在不明显降低导航精度的前提下尽量减少观测的陆标。如果能从时间的角度规划观测时序,就能减少陆标观测带来的图像处理计算负担,但目前缺乏此类研究。

针对上述问题,为减少VAIN系统在处理序列图像时的计算负担,本文针对未知环境中VAIN的最少陆标观测次数开展了研究,并提出了序列图像观测时序规划方法。通过分析离散时间VAIN模型可观测性矩阵的秩,得到了未知环境下保证导航系统状态收敛的最少陆标观测次数。推导了观测陆标时的深度估计误差模型,通过优化该模型可以求解最优观测间隔时间,同时分析了最优解的存在区间,结合可观测性分析结果构建了观测时序规划方法。数值仿真验证了可观测性分析的正确性,并验证了所提出的观测时序规划方法减少观测次数的有效性。

1 视觉辅助惯性导航模型

本章中将建立视觉辅助惯性导航的连续时间、离散时间状态方程,以及测量方程,这是滤波器设计和可观测性分析的理论基础。

1.1 连续时间状态方程

本文研究的着陆器利用IMU和光学相机进行自主导航。定义如下坐标系:着陆坐标系{L},着陆器本体坐标系{B},如图1所示。着陆坐标系定义为固定在行星表面的参考坐标系,它的xL-yL平面在着陆平面上,zL轴指向天空。着陆器本体坐标系{B}固定在着陆器上,它的原点在着陆器质心处,用C表示。

图1 着陆器与着陆点的观测几何Fig.1 Observation geometry of the lander and landing site

着陆器的连续时间状态方程如式(1)所示[16]

(1)

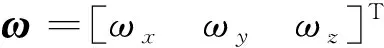
IMU的输出加速度和角速度分别为aimu和ωimu:

(2)

式中:C(q)为q对应的姿态转移矩阵;g为着陆系{L}下的重力加速度;ωi为着陆系{L}下的行星旋转角速度;na和nω为零均值高斯白噪声形式的测量噪声。

本文仅研究行星旋转角速度较慢的着陆情况,为了简化后续推导,给出如下假设[7]:

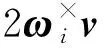
假设 2.着陆器在着陆段内的IMU漂移偏差ba和bω是小量,可以忽略。

(3)

系统状态向量可定义为

(4)

1.2 离散时间状态方程

(5)

(6)

(7)

(8)

(9)

(10)

式中:右上角标(i)为第i个采样时刻,(j,i)为从第i到第j个采样时刻;右下角标ns,np为观测ns个已知陆标和np个未知陆标;Δt为采样周期;I3∈R3×3为3×3的单位矩阵;03×3∈R3×3为3×3的零矩阵;ti为第i个采样时刻对应的时间。

1.3 测量方程

第k个采样时刻的测量值是所有观测到的陆标相对着陆器的方向在{B}中的表示:

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

式中:η(k)为测量噪声。利用扩展卡尔曼滤波器对状态方程和测量方程进行滤波即可同时估计着陆器与未知陆标的状态。

2 可观测性分析

在着陆器上计算资源有限的情况下,必须尽量减少陆标观测次数。但是对陆标的观测次数过少会使导航系统状态不收敛,即不可观测。本章通过分析未知环境中离散VAIN系统可观测性矩阵的秩,获得保证状态收敛的最少陆标观测次数。

在未知环境中,当着陆器仅观测未知陆标时,着陆器在着陆坐标系{L}下的位置和偏航是不可观测的[6]。如果选择图像中的某一个陆标作为着陆系{L}的原点并进行观测,就可以将该陆标看作{L}系中位置已知的陆标。当观测一个已知陆标和任意个未知陆标时,仅偏航角是不可观测的[8]。如果将预定着陆点附近的陆标选做{L}系原点,着陆器就会对预定着陆点进行导航;如果预定着陆点在视场外,可将视场中一个陆标选做{L}系原点,飞行一段时间后再更换视场中另一个陆标为原点,直至预定着陆点出现在视场中。因此,为了在未知环境中使更多状态可观测,下面研究观测一个已知陆标和任意个未知陆标的情况。

从任意第k个采样时刻开始观测N次后,离散时间VAIN模型和的可观测性矩阵表示为[17]:

(19)

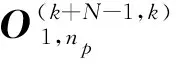
(20)

(21)

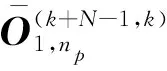
(22)

定理 1.对于观测1个已知陆标和任意个未知陆标的VAIN系统,对相同陆标最少观测3次就能使系统除偏航角外的状态可观测。

(23)

可以看出γ=6+3np<8+3np不满足秩条件。

(24)

定理 1给出了使系统状态可观测条件下,对相同陆标的最少观测次数,可为观测时序规划中的陆标切换提供理论依据。虽然无论是否观测未知陆标,观测3次已知陆标后秩条件均成立,但未知陆标的观测能提高可观测度,提升导航精度。

3 观测时序规划

在着陆器计算资源受限的条件下只能运行有限次图像处理算法,因此需要减少陆标观测次数。可观测性分析给出了保证系统状态收敛的最少观测次数。在少量观测的前提下,为了不明显影响导航精度需要合理规划陆标观测时机。本章从时间的角度规划陆标的观测时序,使着陆器在深度估计误差最小的时刻才观测陆标,从而减少观测次数,并降低观测后图像处理带来的器上计算压力。

3.1 深度估计误差模型

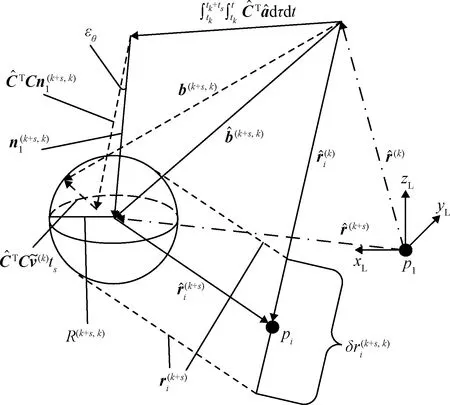
图2 深度估计误差示意图Fig.2 Depth estimation error

(25)

(26)

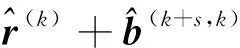
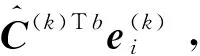
(27)

然后计算实际位置到估计位置的误差界。这里只考虑两次观测之间的状态估计误差引起的深度估计误差,因此实际位置到估计位置的误差界等同于实际基线与估计基线之间的误差界:

(28)

(29)

最后计算深度估计误差。在时刻tk+ts估计的观测方向为

(30)

(31)

(32)

3.2 观测间隔时间优化

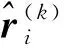
(33)

(34)

此时,通过式(35)来求解最优观测间隔时间

(35)

式中:目标函数Γ的是个单变量一维函数,对其优化所需迭代次数和计算量都相对较小。

3.3 最优解的存在区间分析

(36)

(37)

证.式(34)对间隔时间ts的一阶导得到

(38)

Γ1=R(k+s,k)

(39)

(40)

(41)

(42)

(43)

(44)

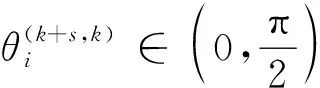
式(36)表示着陆器速度具有朝向地面的分量,这一条件在着陆器下降阶段很容易成立。式(37)表示着陆器的速度方向与所有观测陆标的视线方向夹角小于90°,即着陆器靠近陆标飞行。

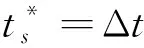
(45)

3.4 观测时序规划策略

在着陆过程的起始时刻首先利用条件数[14]等方法从当前时刻拍摄的图像中筛选出对导航精度贡献最高的几个陆标。根据定理 1,每次观测新陆标后需要至少三次观测。因此在筛选出一组新陆标后,分别在观测第一次和第二次结时利用式(34)计算出相应的间隔时间。在观测完三次后的下一个采样时刻重新筛选一组新陆标,并重复以上过程。

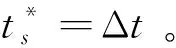
完整的观测时序规划策略如图3所示,图中round表示四舍五入取整。

图3 观测时序规划策略Fig.3 Observation timing planning strategy

4 仿真校验

本章仿真着陆器着陆于火星表面的过程。轨道由多项式制导律生成,着陆过程持续198 s,导航滤波的采样周期Δt=1 s,陆标均匀分布在火星表面。着陆器在着陆坐标系下的初始状态如表1所示:

表1 着陆器初始状态Table 1 Initial state of the lander

4.1 可观测性分析

首先利用蒙特卡洛仿真验证可观测性分析的正确性,设初始位置估计误差范围±1000 m,初始速度估计误差范围±10 m/s,初始姿态估计误差范围±2°,服从均匀分布。

1) 状态收敛

以未知陆标个数np=3为例,分别对已知陆标个数ns=0和ns=1两种情况进行仿真,每个时刻均观测陆标,观测3次后随机更换陆标。仿真300次后导航误差的3σ包络曲线如图4所示。

图4 不同特征点个数时的导航误差Fig.4 Navigation errors with different numbers of landmarks

从图4可以看出,当ns=0时,着陆器的位置和偏航不收敛;当ns=1时,着陆器的位置能够收敛,只有偏航不收敛。由此可知,在未知环境中将着陆系{L}的原点建立在一个陆标上后可获得更多可观测状态,与第2章中的分析相符。

2) 最少观测次数

当ns=1且不更换陆标时,分别对np=0、1、2、3这四种情况进行仿真,并计算相应的可观测性矩阵的秩γ,如图5所示。

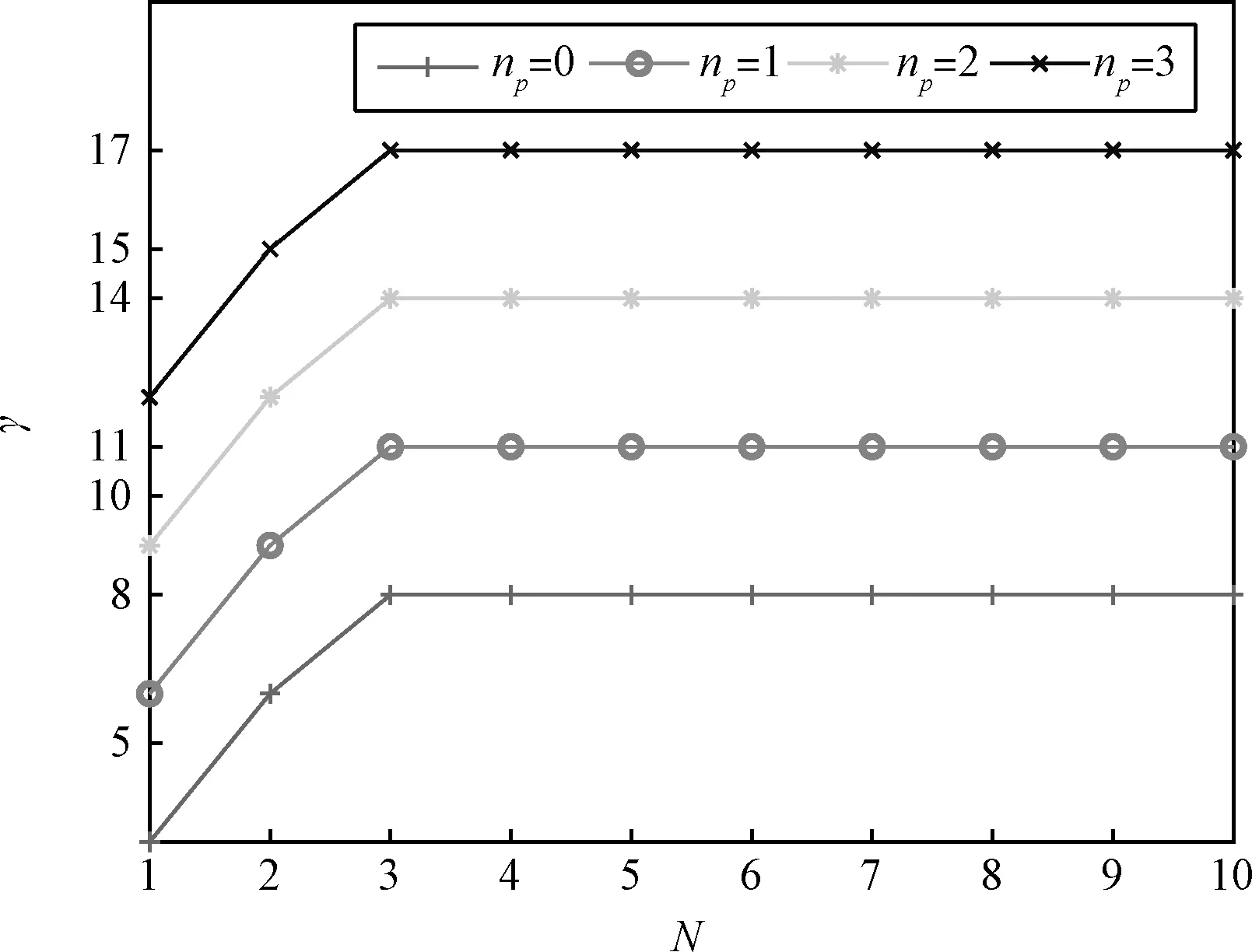
图5 不同特征点个数时的γFig.5 γwith different numbers of landmarks

从图5可以看出,γ随观测次数N增加而增大,可观测的状态增多。表明对于不包含距离信息的基于序列图像自主导航,需要连续多次观测相同陆标才能增加可观测状态的个数。当观测次数N=3时,无论np取任意值γ都达到最大且满足可观测性秩条件(式(22)),此时仅有偏航角不可观测。由此可知,当观测1个已知陆标和任意个未知陆标时,对相同陆标最少观测3次就能使系统除偏航角外的状态可观测,这与定理 1相符。

4.2 观测时序规划

下文验证观测时序规划方法对减少观测次数的有效性。文献[8]通过试验发现增加过多未知陆标也不会明显提高导航精度,因此本文取未知陆标个数np=2,此时导航滤波状态数及相关滤波矩阵位数都不会大量增加。将观测时序规划的自适应观测间隔与每个采样周期都观测陆标的等观测间隔进行对比,如图6和图7所示。设置观测时序规划策略中最大观测间隔时间tsmax=20 s。

图6 不同观测时序的着陆轨迹对比Fig.6 Landing process with different observation timing

图7 观测时机规划效果对比Fig.7 Effect comparison of the observation timing planning

图6是等观测间隔和自适应观测间隔下单次着陆过程的对比。xL-yL平面内的颜色表示行星表面的高度。图6(a)显示等观测间隔的前两次观测之间只间隔一个采样周期,导致观测次数较多;而图6(b)所显示的自适应观测间隔可以明显延长观测间隔,从初始高度6570 m下降到1200 m左右的过程中只进行了9次观测,减少了大量不必要的观测和图像处理次数。

蒙特卡洛仿真300次后的结果如图7所示。图7(a)-(c)显示了自适应观测间隔的导航精度与等观测间隔相差无几,甚至yL和zL方向的位置误差收敛更快。图7(d)统计了蒙特卡洛仿真300次后,所有仿真在每个采样时刻处的观测次数。对于任一时刻,如果每次仿真时都在该时刻观测陆标,则观测次数为300。等观测间隔的导航过程在个采样时刻都进行观测,因此每个采样时刻的观测次数都是300次;自适应观测间隔能延长两次观测的间隔时间,大幅减少了120 s前的观测次数,完整着陆过程的总观测次数相比等观测间隔减少了45.9%。这是因为在120 s之前,状态估计误差较大,需要增大基线长度来减小深度估计误差;120 s之后导航误差已经收敛,增大基线长度反而会增加深度估计误差,需要连续观测陆标以维持导航精度。因此可以看出观测时序规划方法可以在不明显影响导航精度的前提下,自适应地延长观测陆标的时间间隔,从而减小着陆器上处理图像的计算负担。在实际工程中,观测间隔会设计为一个适应着陆器上计算约的数值,在此基础上采用自适应观测间隔能从理论上进一步减少不必要的观测次数,节省更多计算资源。