基于计算教学 培养推理能力——“小数乘整数”教学片段与思考

江苏省南京市金陵中学河西分校小学部 沈利玲

一、学习内容

苏教版数学五年级上册第55～56页例1、“试一试”和“练一练”，第58页“练习十”第1～4题。

二、教学学习重点

探索并掌握小数乘整数的计算方法，会用竖式进行计算。

【学习难点】

理解计算小数乘整数时，积的小数点定位的道理。【预设过程】

流程一：复习导入，初步感知

提问：同学们，知道今天我们研究什么内容吗？

谈话：今天我们研究小数乘整数，其实关于这个内容，我们之前在认识小数时就已经会口算了，不信你看。

1.小数的计数单位乘整数

（1）出示图1：

图1

提问：图中的涂色部分用小数表示是多少？你是怎样想的？

明确：把这个正方形看作单位“1”，平均分成10份，其中的一份就是0.1，3份是0.3。

提问：3个0.1，我们可以怎样列式？

明确：0.1×3＝0.3，同学们看，这道算式就是一道小数乘整数的算式。

（2）出示图2：

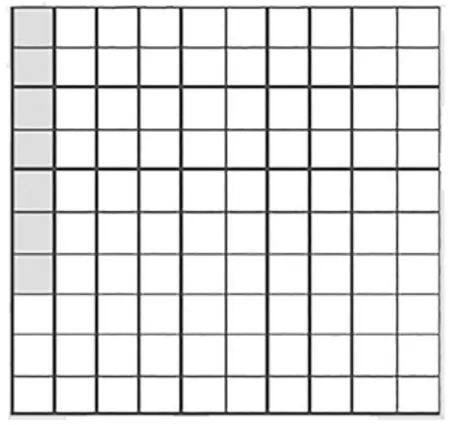
图2

提问：这里的涂色部分用哪个小数表示？

提问：0.03里面有多少个0.01？你能列出一道乘法算式吗？

明确：0.03里面有3个0.01，0.01×3＝0.03。

出示图3：

图3

提问：如果涂这样的43份呢？算式怎样列？结果是多少？

明确：0.01×43＝0.43，涂色部分是0.43。

（3）出示图4：

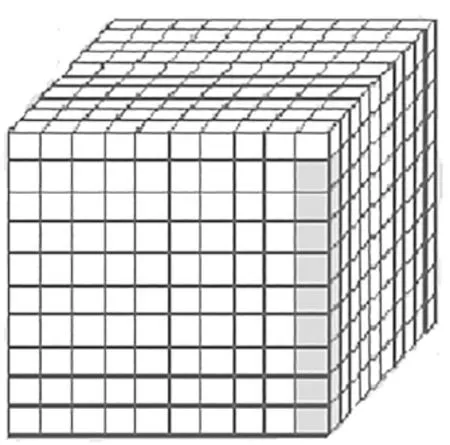
图4

提问：这里的涂色小方块用哪个小数表示？谁会像这样列一道算式？

明确：这里的涂色小方块用0.009表示，算式是0.001×9＝0.009。

追问：如果是这样的347个小方块呢？怎样列式？

明确：0.001×347＝0.347。

2.观察尝试发现规律

提问：这些算式都是小数乘整数，仔细观察，算式中都是什么样的小数？

指出：都是小数的计数单位乘整数，因此结果能很快口算出来。

谈话：刚刚我们得出，几个0.1的积就是一位小数，几个0.01的积是两位小数，几个0.001的积是三位小数，你认为积的小数位数和谁有关？有什么关系？同桌之间互相说一说。

“小数乘整数”内容本身对学生来说并不难，但之前学习的“小数加减法”对学生具有负迁移作用，容易让学生产生这样的想法：计算小数乘整数时也要做到小数点对齐。因此，深入理解算理即小数点如何定位是本节课的难点之一。课的开始，教学特殊的小数乘整数，即小数的计数单位乘整数，教师从学生原有知识导入，让学生利用小数意义的知识来解决，初步感知小数乘整数就是计算有多少个计数单位。因此，积有几位小数主要看计数单位。另外，由于在竖式计算中，学生容易观察到积的小数点和因数的小数点对齐，干扰了思考。而口算中的积是直接写出来的，学生通过观察能够很快发现积的小数位数和因数的小数位数的关系。除此之外，教师还为新课教学做好铺垫，虽然学生在算0.8乘3时就是利用了8个0.1乘3得24个0.1，但是他们并不理解，通过此段教学，就可以有效地帮助他们突破这一难点。

3.练习

出示：0.1×45 0.01×124 0.001×245

（学生独立完成，全班订正）

谈话：通过这些例子，确实发现因数中有几位小数，积就有几位小数。前面，我们说这些都是比较特殊的小数乘整数，我们要学的仅仅是这些特殊的小数乘整数吗？下面，我们继续研究。

流程二：自主探索，掌握算理

1.教学例1第（1）小题

（1）尝试计算

出示题目（见图5）：

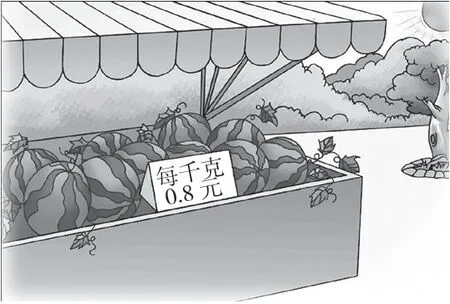
图5

谈话：从图5中，你知道了什么？买3千克西瓜要多少元？

列式：0.8×3＝2.4（元）

提问：我们刚刚只学习了0.1、0.01、0.001这样的小数计数单位乘整数，“0.8×3”这样的一般小数乘整数还没有学，你们确定结果就是2.4元吗？怎么证明呢？在本子上写一写。

汇报：

①0.8元＝8角，8×3＝24角，24角＝2.4元。

指出：结合具体的情境，利用单位换算得出结果是2.4元。

②0.8×3＝0.8＋0.8＋0.8＝2.4。

明确：“0.8×3”就是3个0.8相加，我们可以摆一道加法竖式。

提问：这道加法竖式是怎样算的？

明确：先算十分位“8＋8＋8”，即8×3＝24，再点上小数点。

提问：这里的8表示什么？得到的24呢？

明确：这里的8表示8个0.1，24表示24个0.1，所以结果是2.4。

③0.8是8个0.1，8个0.1乘3得24个0.1，是2.4。

谈话：把这道算式转化成之前的0.1乘一个整数，我们也可以用算式来表达，0.8×3＝8×3×0.1＝24×0.1＝2.4。仔细观察这三种证明方法，都要先算什么？

明确：不论是单位换算还是算加法还是想成0.1乘一个整数，都要先算8×3＝24。

（2）尝试竖式计算

提问：如果这题列竖式该怎样写呢？自己试一试。

学生尝试，汇报：

提问：你们同意哪一种？为什么？

（学生交流）

板书： 0.8 ×3=2.4（元）

（引导学生理解直接用乘法竖式计算的算理）

提问：这里的8表示什么？

即理解8个0.1乘3得24个0.1，24个0.1是2.4。

可以结合学生的回答，出示图6：

图6

可以先出一个正方形，说明：把正方形看作“1”，每个正方形平均分成10份，1份是0.1（十分之一），涂色部分表示8个0.1，就是0.8（十分之八），然后出示3个0.8，再把它合并，3个0.8是24个0.1，让学生清楚地知道3个0.8是2.4。

以数形结合的方法帮助学生理解8个0.1乘3得24个0.1，24个0.1也就是2.4，更有利于学生深入理解小数乘整数的算理，同时对小数的意义有更充分的认识。

提问：想一想，计算“0.8×3”，我们要先算什么？

明确：先算“8×3”，因此3和8对齐。

提问：算完8×3＝24，这道题就写好了吗？还要干什么？

明确：还要点上小数点。

提问：小数点点在什么位置？为什么？

明确：因数中有一位小数，积就有一位小数。我们就从积的右边数出一位点上小数点。我们还要理解其中的道理：8表示8个（0.1），24表示（24个0.1），是2.4。

学生用已有知识证明0.8×3＝2.4的过程其实就是理解算理的过程，发现可以从乘法的意义来思考，“0.8×3”表示3个0.8相加，也可以从生活经验——元、角的关系理解，从小数意义这个数学本源知识的角度理解小数乘整数的算理。教师通过一个问题“这几种证明方法都是先算什么”凸显小数乘整数的根本是“先按照整数乘法算出积”，并以此作为摆竖式的依据。之后的练习设计巧妙且直指核心，通过两小题的对比，既巩固了小数乘整数要先按照整数乘法算出积的知识，又使学生深入理解了如何点小数点的道理。

2.教学例1第（2）小题

（1）出示题目

提问：冬天每千克西瓜2.35元，买3千克西瓜要多少元呢？

先估算：（1）冬天买3千克西瓜，6元够吗？（2）10元够吗？

通过估算，学生先大致了解计算结果的范围，再进行计算，有利于更好地把握计算结果的合理性。

提问：“2.35×3”的结果是多少？请大家先试着算一算，再和同桌交流你是怎样算的。

明确：235个0.01乘3得705个0.01，所以积是两位小数。

（2）教学“试一试”

出示题目：观察下面的算式，先猜一猜积可能是几位小数，再用计算器计算。

4.76×12＝ 2.8×53＝ 103×0.25＝

3.小结算法

小数乘整数，先按整数乘法进行计算，再看因数中有几位小数，就从积的右边数出几位点上小数点。

教师引导学生通过观察、猜想、尝试、归纳等活动发现小数乘整数的计算方法，发展了合情推理能力。

流程三：巩固练习，深化新知

流程四：全课小结，布置作业

三、收获与反思

运算和推理在数学中具有重要的地位。新课标指出，在义务教育阶段，数学思维主要表现为运算能力、推理意识或推理能力。通过经历独立的数学思维过程，学生能够理解数学基本概念和法则的发生与发展，数学基本概念之间、数学与现实世界之间的联系；能够探究自然现象或现实情境所蕴含的数学规律，经历数学“再发现”的过程；发展质疑问难的批判性思维，初步养成讲道理、有条理的思维品质，逐步形成理性精神。

具有一定的推理能力是培养学生数学素养的重要内容，也是数学课程和课堂教学的重要目标。学生对算理的深刻理解，少不了教师适时与精心的点拨。这就要求在计算教学中，教师要针对计算的连接点、受阻点、易错点等关键处，不仅要强调“怎么做”，还要注意引导学生思考“为什么这样做”，从而让学生深刻理解算理，轻松建构算法。

教师在教学过程中要注重对学生推理能力的培养，让学生愉悦、自主地参与数学教学活动，在活动过程中感悟推理的方法和魅力，提高学生的推理能力，达到理想的教学效果。