以问引学明晰进位本质 整体建构发展运算能力
——“两位数加一位数的进位加法”的思考与实践
2023-04-10安徽省合肥市庐阳区教育体育局教研室李玲玲
安徽省合肥市庐阳区教育体育局教研室 李玲玲
安徽省合肥市六安路小学中铁国际城校区 吴 安
新课标指出,要使学生感悟数与运算本质上的一致性。而数的认识和数的运算是相互统一的,其数学核心要素聚焦在数位、计数单位、位值制和十进制计数等方面。笔者“三思而后行”,力求探寻运算能力素养落地的实施路径。
一、一思:内容前后关联
1.知识前后联系

已学内容单元内容后续内容10 以 内 加、两位数加一位数减法(进位) 百以内的连加、连减和加、减2加0 法以内进位?(两退位位数)减一位数?混合20 以内退位两位数加两位数减法(进位) 万以内的加法100 以内加、两位数减两位数和减法减法(退位)
两位数加一位数进位加法的内容是学生从100以内不进位、不退位运算向进位、退位进阶学习的开启内容。
2.单元内容分析
从单元整体视角分析发现,两位数加、减一位数的口算是以10个一是1个十为基础的概念建构课,是学生从数的认识向数的运算认知十进制计数原理的一次重要跨越,是学生理解加、减中进位和退位运算联系和迁移的重要基石。(如图1)

图1
二、二思:学生已有水平
为了更真切地了解学生学习的现实起点,我们分别从能算出结果、掌握算法、理解算理、选择合理简洁的运算策略等方面对校区学生进行抽样检测。
通过对图2问题单中计算结果统计发现,能算出结果的学生约占78%,能掌握算法的约占67%,而理解算理的约占31%,能用多种方法计算的约占34%。由此可知,学生已经具备一定的运算能力,只是运算的算理及算法之间的关联意识薄弱,对十进制计数原理下的进位加法本质感知不深。

图2
三、三思:教学存在疑难
笔者在访谈教师关于教学情况时发现一些共性问题:
(1)学生的计算没有太大问题,因此通过小棒操作得出结果的价值不够突出,操作时有一种无处着手之感。
(2)虽然大部分学生会算,但教师在课堂中还是将教学重点落在学生计算技能的训练上,学生运算素养不高。
基于以上现实情况,笔者确定这节课的教学重点是理解两位数加一位数的算理、算法之间的关联,能比较熟练地进行计算;难点是帮助学生理解十进制计数原理下“满十进一”的进位加法本质。
笔者通过比较、分析,借助直观的学具模型——小棒和半抽象学具模型——计数器,以问引学,用操作突破学生关于“10个一是1个十,即个位相加满十向十位进一”算理的认知壁垒,在先“扶”再“放”的过程中让学生感受算法多样化,再逐层对比,引导学生感受数学探究的层次性,尝试带领学生触及进位加法的概念本质。
一、多元表征促理解,显化进位概念
“数学学习要重视知识的形成过程,过程与结果并行;重视直观表述,直观与抽象并重;经历数学再发现的过程,探索发展学生核心素养的路径。”基于大多数学生已经能计算出结果的学情,教学需要突破进位加法的认知盲点。为外显满十进一的进位计算原理,在实际教学时,应以关键问题引领,让学生借操作的直观过程理解抽象的进位本质,让概念建立可视化。
师:24里原来明明只有2个十,怎么得到3个十呢?多出的1个十从哪来的?你是怎样想的?先用小棒摆一摆或用计数器拨一拨,再和同桌说一说。
生1:我是用小棒摆的,24,先拿2个十和4个1,加6,4+6=10,10+20=30,多的1个十就是4+6=10。
师:和你想的一样吗?多的那个十在哪里?(圈画10个一得到1个十)
生2:我是拨计数器的,先拨24,加6,在个位上再拨6颗珠子,4+6=10,满十退回,再在十位上拨1颗珠子,这就是多的1个十,合起来是30。
操作的直观价值在这里凸显。相较于用小棒或者计数器得出结果或者验证结果的要求,“24里原来明明是2个十,怎么得到了3个十呢?多出的1个十是从哪来的”对学生来说是一个全新的探究问题,也是需要操作予以解释的,避免了学生明明已经会算,还被强行要求操作的尴尬,此时问题“多出的1个十是从哪来的”让原本不易理解的4+6=10、10+20=30的算法中似明非明的“10个一是1个十”的认知盲点以多元表征的方式直观呈现。从实物小棒到更具抽象的计数器,再到用分解式记录计算过程,层层递进,以操作促进算法、算理的融合,将“10个一是1个十”的认知经验与“满十进一”的进位本质进行有效关联和沟通。
二、变式对比析本质,强化进位意义
课堂教学要遵循学生的思维特点和认知规律,需要在新旧知识和可迁移知识间搭建对比支架,让学生从宏观上思考,建立数学对象之间的逻辑关系,揭示本质属性。为更好地让学生让学生感受满十进一,设计适时的对比、辨析可以凸显进位本质。本节课注重设计对比性问题的探究,引导学生在数据的观察、比较、发现中激活思维、发展思维、深化思维,在对比过程中强化十进制计数原理下的进位加法意义。
片段一:
在教学完24+6=30后,笔者设计了一组变式练习。
变式练习:
6+24=30 25+5=30 21+9=30 27+3=30
师:仔细观察这些算式及得数,你有什么发现?
生1:算式都是二十几加几,得数都是30。
生2:加数都是2个十,得数都是30,3个十。
师:这里的加数都只有2个十,得数却都是3个十,怎么多了1个十?
生:个位上相加等于10。
师:个位相加满十,向十位进一,这就是数学上说的满十进一的规律。(板书:满十进一)
片段二:
在探究完24+9=33后,再把今天学习的内容和课前复习的计算进行对比。
师:这是我们刚才解决的两个问题,结合之前的计算,仔细观察图3,比较左右两边算式及得数,你又有什么发现?
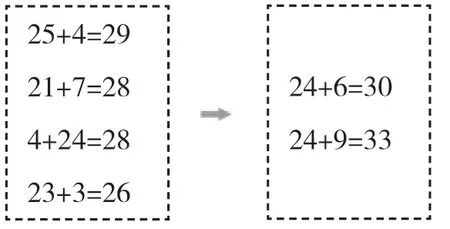
图3
生1:都是二十多加几。
生2:前面的得数都是二十多,后面的是三十和三十多。
生3:之前学的没有进一个数,这次学的进了一个数。
师:你的意思是从2个十变成3个十吗?那进的1个十是从哪来的?
生:个位上相加满十就向十位进一。
经历前面的操作经验,第一次凑整的进位对比铺垫,学生能够感受到两位数加一位数的进位其实就是要个位相加满十,得数从原来的2个十进位相加得3个十;通过对24+9=33的计算,学生能够感知到虽然口算的方法不一样,但是都是个位加起来超过十需要向十位进一;再到最后和之前学习的不进位的加法进行对比,学生能够感受到两位数加一位数进位与不进位的前后联系与区别,建构两位数加一位数的加法认知体系。
三、精编练习促巩固,提升进位技能
适量、适度、有层次性的练习可以有效巩固所学;关键处提出反思性问题,可以让学生在学中练、练中思,有效提升学生的学习力和思考力。
如图4中第1题,为进一步让学生熟练满十进一的计算方法,教师提供思考支架,要求会说先算什么、再算什么,思考有没有不同的方法,让学生在多种算法中发展口算技能。

图4
如图5,第2题以题组形式出现,待完成之后,教师追问:观察加数及得数,每组算式间有什么联系?学生在计算之后感受到第一个算式就是下面算式分别先算的部分,得数个位均相同,得数十位在加数的十位上进一,进一步感受两位数加一位数和之前学习的20以内进位加法之间的联系与进阶。
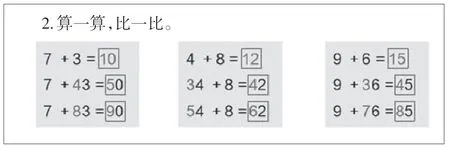
图5
如图6,第3题以发展学生的思维为主,教师提问“35+□可能等于几十多”引发学生思考。纵观课堂学习,回归学习两位数加一位数内容的本质,感受其进位与不进位之间的区别,即个位相加是否满十,决定是否需要向十位进一,感受知识的纵向生长,进一步完善学生的认知系统,深刻思维结构。
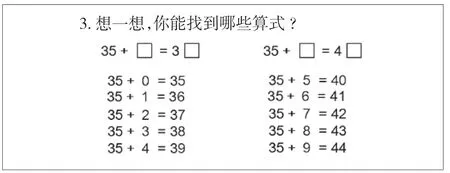
图6
四、建构迁移引思考,延伸运算能力
数学思维的深刻应体现其动态的生成,以点连线,用联结构建知识的立体网络,教学中教师要适时关注学生知识的结构化生长。
师:上学期,我们学习了10以内的加法和20以内的进位加法,这学期学习了不进位的两位数加一位数,今天学习的是进位加法,你觉得接下来要学习什么呢?你会用今天学到的方法解决图7中的问题吗?

图7
以启发性的问题引导学生关注知识的溯源与承接,让学生在联想中抓住学习要点,串联进阶脉络,在类比推理中感知算法都是计数单位的累加,进位加法的算理上孕伏满十进一的十进制计数原理。
“有效的教学活动是教师的教和学生的学的统一。”为落实核心素养下的教学目标,整体把握教学内容,本节课注重单元整体设计,丰富学习方式,有效实施教师和学生“双主体”策略,教师主导提出关键性的探究问题,在对比中引导思索,在反思中提升技能,在启发中有效建构,让学生探究的主体价值充分发挥。利用数形结合的思想,让学生在多样的表征形式中充分感知到“10个一是1个十,满十进一”的十进制计数原理的含义和价值,在发掘进位加法的内核的过程中感受数的认识和数的运算本质上的一致性,培养运算思维的深刻性。
