考虑温度梯度的氧化锆整体叶盘振动特性分析

2023-04-08杨铮鑫孙荣城郑伟党鹏飞

科学技术与工程 2023年6期

杨铮鑫, 孙荣城, 郑伟, 党鹏飞

(沈阳化工大学机械与动力工程学院, 沈阳 110142)

整体叶盘作为燃气轮机、飞机发动机等动力装置的单一结构制造的核心机械部件[1],在高转速、高温度环境下工作,常因高温环境和大温差导致叶片出现复杂的大振幅非线性振动[2]。目前正广泛应用于飞机推进的燃气轮机中的热障涂层(thermal barrier coatings,TBC),其由低导热陶瓷制成,为热流中的叶片等金属部件进行隔热,并降低表面温度[3]。TBC(厚度为100～500 μm)的使用,以及底层高温合金部件的内部冷却,可大幅降低高温合金的表面温度(100～300 ℃)[4]。由此可见,为了降低整体叶盘在高温下大幅度非线性振动,有必要深入了解其在不同温度场下的振动特性。

近些年来,已经有许多研究者对温度场下的整体叶盘和旋转叶片振动特性进行了分析和研究。Dang等[5]基于三阶剪切变形理论和哈密顿原理,考虑旋转叶片在厚度方向上温度场的非线性分布,得到了高温下含单面TBC旋转叶片的软化型非线性因素和非线性动力学行为的演化规律。李蔓林等[6]利用线性插值法和有限元方法对稳态温度场作用下的涡轮叶盘结构振动特性进行确定性分析。艾书民等[7]采用蒙特卡罗仿真方法和热-固耦合方法对涡轮叶片进行了确定性热应力分析。张婷婷等[8]利用有限元方法分析了非旋转状态与旋转状态下稳态温度场对盘片结构耦合振动的影响。杨铮鑫等[9]研究了改变NiCrAlY硬涂层的涂敷方式对整体叶盘的减振效果,发现硬涂层技术可以降低整体叶盘共振点的数量。张宏远等[10]采用子结构模态综合法,从应变能角度分析了叶盘结构频率转向和振型转换特性。方建士等[11]采用Hamilton原理和Rayleigh-Ritz模态法,对旋转悬臂梁的频率转向和振型转换特性进行研究,发现相邻两阶存在频率转向且伴随着振型转换。王培屹等[12]采用参数化建模,对盘片耦合振动频率转向特性进行研究,发现频率转向间隙曲线的改变具有碗状形式,且响应放大与盘片结构刚度有关。但是,以上研究对叶盘和旋转叶片的温度场大多采用线性分布,叶片双面带有TBC以及温度场沿叶片厚度方向呈非线性分布还未涉及。

基于以上问题,在已有研究基础上,现建立叶片两面带有TBC的整体叶盘有限元模型,考虑温度场沿叶片厚度方向呈非线性分布,采用ANSYS的热-固耦合方法和稳态热传导理论相结合,对具有温度场的TBC整体叶盘进行模态分析及频率转向区的谐响应分析,对比分析不同温度场对TBC整体叶盘振动特性影响。

1 有限元模型及温度场建立

1.1 有限元模型

某航空喷气发动机的一级整体叶盘,叶片沿周向均匀分布。如图1所示,基于悬臂梁功能,通过Creo软件创建了该叶盘的实体模型,并使用ANSYS软件对其进行网格化划分,创建TBC整体叶盘有限元模型,TBC选用SHELL181单元网格,整体叶盘选用SOLID187单元网格,设置网格大小为2 mm,共划分节点数为296 035,单元数为114 411,如图1所示。TBC整体叶盘主要几何参数如表1所示,材料参数如表2所示。

图1 TBC整体叶盘有限元模型Fig.1 Finite element model of TBC blisk

表1 TBC整体叶盘的几何参数Table 1 Geometric parameters of TBC blisk

表2 TBC整体叶盘的材料参数Table 2 Material parameters of TBC blisk

1.2 温度场的建立

为了研究温度场沿叶片厚度方向呈非线性分布的可行性,假设温度仅沿叶片厚度z方向变化,且板平面内的一维温度场恒定,建立了3种沿叶片厚度方向不同分布方式的温度场,具体如下。

(1)方案1:双面TBC温度为1 100 ℃,基体温度为750 ℃。

(2)方案2:采用一维插值方法,对带有TBC叶片沿厚度方向一维稳态温度场进行线性分段插值拟合。

(3)方案3:利用一维稳态热传导理论,非线性温度分布公式[13]为

(1)

式(1)中:T为叶片厚度方向的温度;z为变量;Tc和Tm分别是TBC和叶片的表面温度;h为叶片厚度;k为材料的传热系数。

通过多项式级数,非线性温度分布公式被改写为

T(z)=T+(Tc-Tm)×

(2)

式(2)中:数项级数NT=5;TBC的传热系数kc=1.7;基体的传热系数km=1;体积分数指数n控制材料在厚度z方向上的轮廓。根据参考文献[14]中的材料属性,作3种方案分布曲线图,如图2所示。

图2 3种温度分布曲线Fig.2 Three temperature distribution curves

2 TBC整体叶盘不同温度场的振动特性分析

基于以上3种温度场方案,采用ANSYS有限元方法对TBC整体叶盘进行有限元模态分析,选取转速为0、200 rad/s,分别求解得到TBC整体叶盘的前72阶模态频率。在转速为0时,提取TBC整体叶盘在不同方案之间模态频率的差值,并作模态频率差值图,如图3(a)所示;在转速为200 rad/s时,提取TBC整体叶盘在不同方案之间模态频率的差值,并作模态频率差值图,如图3(b)所示。

2-1、3-2分别为方案2与方案1、方案3与方案2的模态频率差值图3 不同转速、不同方案间的模态频率Fig.3 Modal frequency under different speed and programme

由图3(a)可以看出,方案2与方案1的模态频率差值在0～1范围内,方案3与方案2的模态频率差值在2.0～3.5范围内;由图3(b)可以看出,方案2与方案1的模态频率差值在0～1.5范围内,方案3与方案2的模态频率差值在4.5～6.5范围内。由图3还可以看出,转速一定时,3种温度场对叶片一阶(1～18阶)模态频率影响较大,而方案3温度场对叶片一阶(1～18阶)模态频率影响最大。由此说明:相比方案1和方案2的温度分布方式,非线性温度分布的温度场导致TBC整体叶盘模态频率降低幅度较大,对叶片一阶模态频率影响最大。

3 非线性温度梯度下TBC整体叶盘振动特性分析

根据相关文献[15],整体叶盘前后面所处温度场不同,且叶片的迎风面温度较高。为了TBC整体叶盘所处的温度场更加贴近实况,采用非线性温度梯度分布的温度场,考虑温升对TBC整体叶盘振动特性的影响,建立了3种不同工况下的温度场。①工况1:TBC上表面温度为700 ℃,TBC下表面温度为500 ℃;②工况2:相比工况1,TBC表面温度提高200 ℃;③工况3:相比工况2,TBC表面温度提高200 ℃。

3.1 模态频率分析

为了研究温升对TBC整体叶盘振动特性的影响,依据以上3种工况,且每种工况设置了转速为0、200 rad/s,采用ANSYS有限元方法对TBC整体叶盘进行模态分析。提取TBC整体叶盘前18阶模态频率,作TBC整体叶盘分别在转速为0、200 rad/s时、不同温度场状态下的各阶模态频率图,如图4所示。

图4 不同转速、不同工况下的模态频率Fig.4 Modal frequency under different speed and different condition

由图4可以看出,在转速一定的情况下,升高温度,各阶模态频率明显降低。这是因为温度的升高使得材料弹性模量下降,导致模态频率下降。由图4还可以看出,在温度场一定的情况下,转速越高,各阶模态频率增大。

为了研究离心力在温度场状态下对TBC叶盘振动特性影响,在工况一定的情况下,分别设置了转速ω1=0、ω2=200 rad/s、ω3=800 rad/s。提取TBC叶盘前18阶模态频率,作TBC整体叶盘在同种温度场时、不同转速之间模态频率增值量纲图,如图5所示;作TBC叶盘在一定转速时、不同温度场状态之间模态频率差值量纲图,如图6所示。

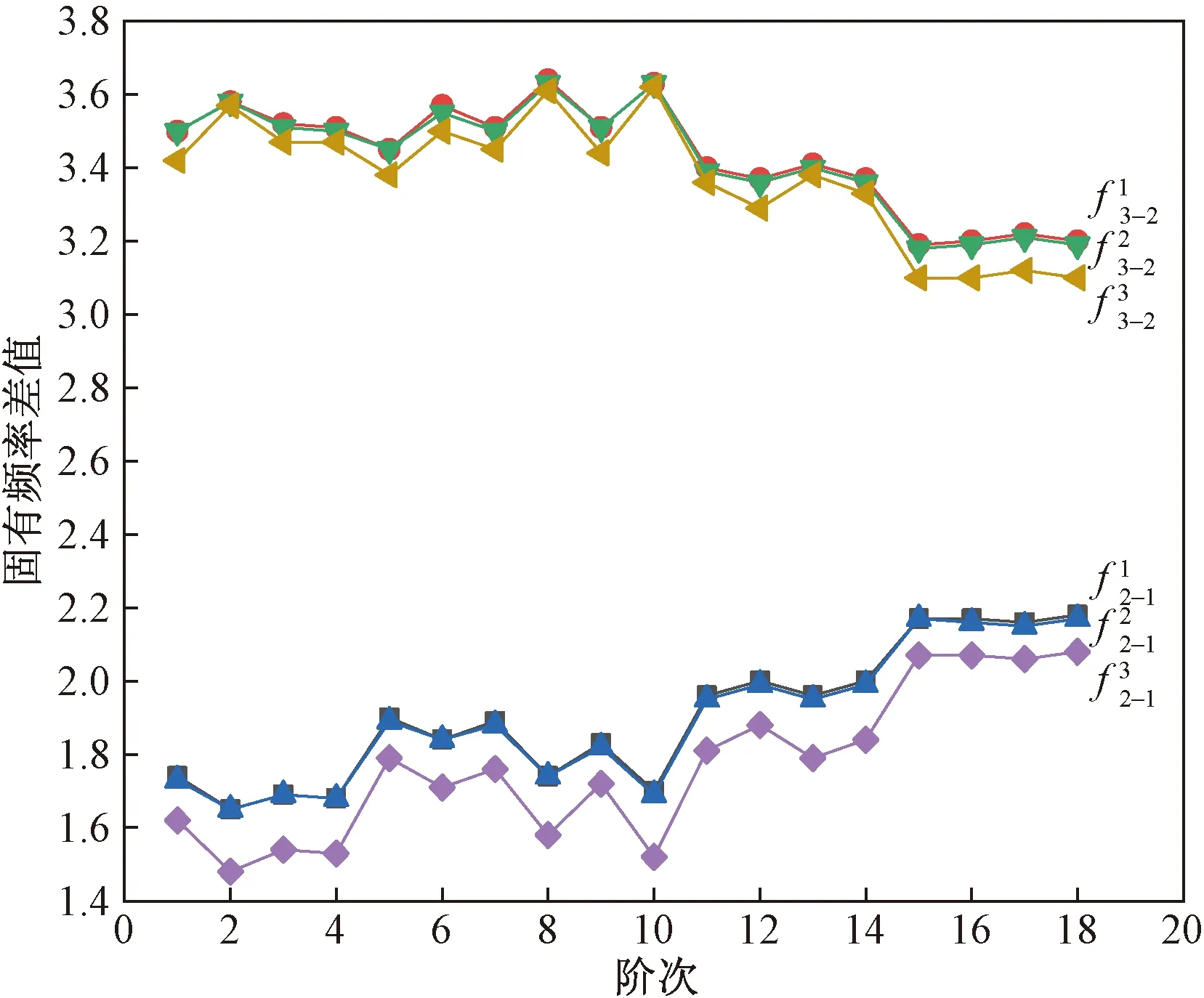
和分别表示在工况r时ω2相对ω1状态下和ω3相对ω2状态下模态频率增值量纲图5 模态频率增值Fig.5 Modal frequency increment

和分别表示在k转速时工况2与工况1和工况3与工况2固有频率差值的量纲图6 模态频率差值Fig.6 Modal frequency difference

由图5可以看出,在同种温度场状态下,转速越高,各阶模态频率越高,且低阶的模态频率受转速的影响比较明显。这是因为转速的增大使得离心力增大,TBC叶盘刚性增大,导致各阶模态频率增大。由图5还可以看出,随着温度的升高,使得材料弹性模量变小,会降低离心力增大导致模态频率增大的程度。由图6可以看出,在转速一定的情况下,温度越大,各阶模态频率降低量越大;随着转速的增大,温度的对模态频率的影响减小。

3.2 频率转向分析

通过对TBC整体叶盘在3种温度场、转速0～1 000 rad/s下进行模态分析,提取其前18阶模态频率并作坎贝尔图,发现5～6阶、7～8阶存在频率转向现象。本文研究对TBC整体叶盘的5～8阶模态频率转向进行分析,并分别作5～6、7～8阶坎贝尔图,如图7所示。在频率转向区提取两阶转向频率差值,即频率转向间隙,对所得频率差值进行归一化处理并作转向间隙量纲值表,如表3所示。

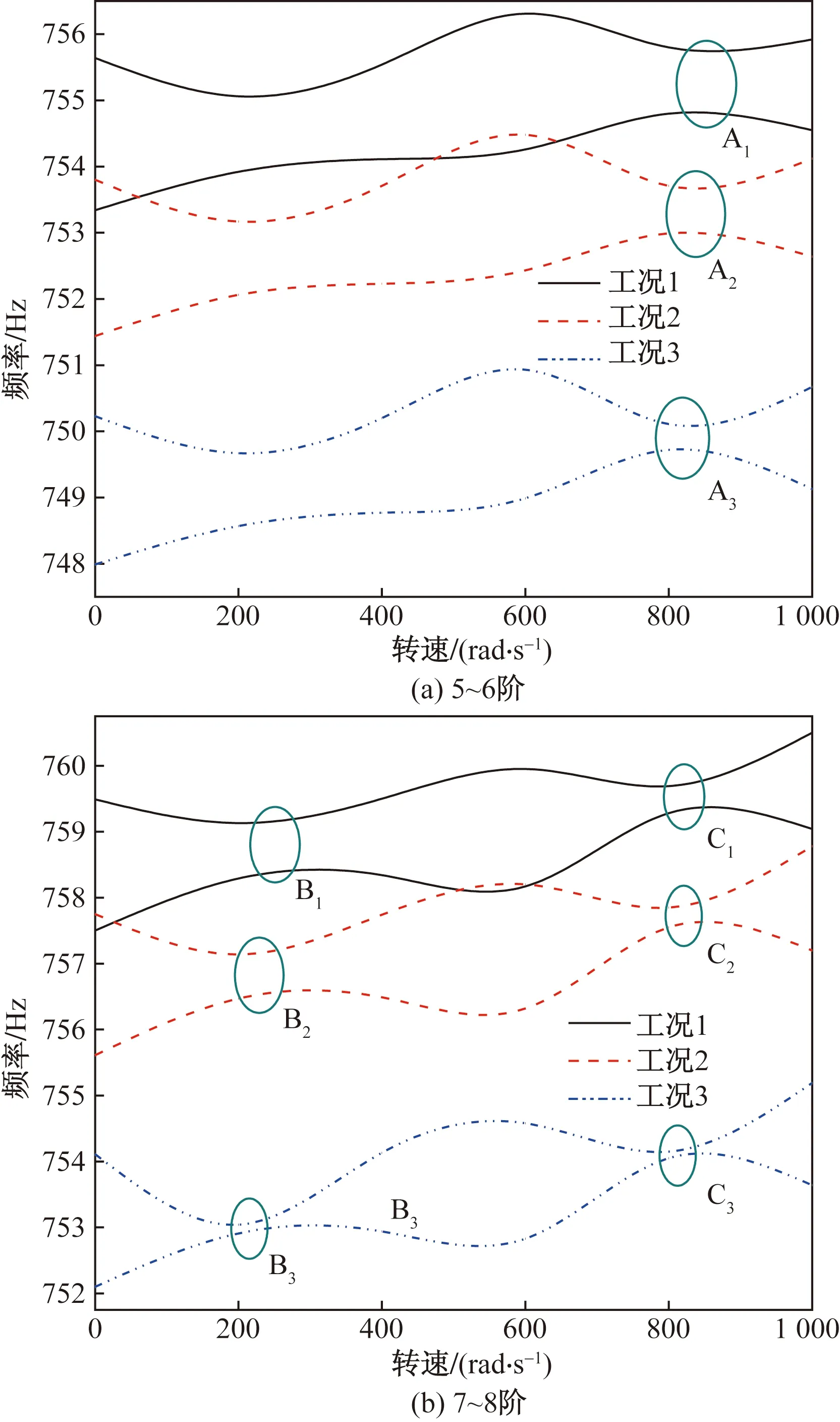
图7 坎贝尔图Fig.7 Campbell diagram

由图7可以看出,5～6阶存在1处频率转向区,转向转速在800 rad/s附近;7～8阶存在2处频率转向区,转向转速分别在200、800 rad/s附近;且随着温度的增大,频率转向区出现左倾的趋势,这是因为温度升高使得材料弹性模量降低所致。由表1可以看出,随着温度的升高,频率转向区的转向间隙逐渐降低。

表3 频率转向区转向间隙Table 3 Steering clearance in frequency steering area

3.3 谐响应分析

为了研究不同温度场下TBC整体叶盘受迫响应特性,选取TBC叶盘模态频率转向区处的转速,采用谐响应分析方法,在0～900 Hz范围内,加载激振力为1g(g为重力加速度)的激振载荷,在不同温度场下对TBC整体叶盘进行谐响应分析。作TBC叶盘分别在转速200、800 rad/s时,不同温度场下受迫响应幅值图,如图8所示。

图8 幅频响应曲线Fig.8 Amplitude frequency response curve

由图8可以看出,在一定转速情况下,随温度的升高,响应曲线呈现左倾的趋势。由图8(a)得到,工况1、工况2、工况3对应的响应峰值为0.047 19、0.049 08、0.050 31 mm,随温度的升高,响应峰值分别增大4.1%、2.5%。由图8(b)得到,工况1、工况2、工况3对应的响应峰值为0.048 49、0.050 18、0.054 74 mm,随温度的升高,响应峰值分别增大3.5%、9.1%。通过对比分析数据,在1g激励条件下受迫响应峰值随温度的升高呈现不同幅度的增大,增大范围在10%以内;且在高转速、高温度状态下TBC整体叶盘受迫响应峰值增大程度较明显。