城市集中供热管网热平衡调节技术研究
2023-04-07张毅
张 毅
(北京市热力集团有限责任公司,北京 100062)
0 引言
城市集中供热管网常因水力失调出现循环流量较低的情况,一般可采取模拟分析法对其进行调节。但由于该方法过于依赖历史经验,导致调节稳定性较差,因此该文提出一种热平衡调节技术,通过构建自力式平衡阀对循环流量进行调节,可有效减小调节偏差[1]。
1 城市集中供热管网热平衡调节技术研究
1.1 城市集中供热管网热平衡计算
城市集中供热管网中,实际流量与预测流量之间如果存在较大差异将会导致水力失调。对城市集中供热管网中的热平衡进行调节,可有效缓解水力失调现象,在保证水力供给压力的同时能够有效提高设备的补水能力,进而提高供热管网的供热能力[2]。对此需要对热平衡相关数值进行计算,具体包括计算水力失调度以及构建集中供热管网的传热方程,具体计算步骤如下所示。
通过计算水力失调度来判断城市集中供热网管是否达到热平衡状态,具体计算公式如公式(1)所示。
式中:x为城市集中供热管网的水力失调度;Vs为热用户实际水体流量;Vg为预测水体流量。
当x的值为1 时,说明此刻城市集中供热管网达到了热平衡状态,无须对其进行调节处理;当x的值大于1 时,说明此刻存在等比失调情况,主要原因是管网堵塞导致管内压力过大;当x的值小于1 时,说明此刻存在不等比失调现象,该现象主要是由供热网管失水过多,供热系统的补水能力无法满足实际需求导致的。通过上述对水力失调度的计算,判断此刻城市集中供热网管是否处于热平衡状态,如果水力失调度不为1,则需要对其进行热平衡调节。对此,需要建立供热管网内部的传热方程,即管网内部与外部之间的换热过程描述方程,具体方程表达式如公式(2)所示。
式中:A为供热管网内部与外部的换热接触面积;tair为供热管网内部空气流通温度;tstf为供热管网实体内部平均温度;Qe为供热管网内部与外部在换热过程中交换的热量值[3];k为换热系数,该值主要受空气对流系数以及供热网管尺寸数值的影响,具体计算公式如公式(3)所示。
式中:hair为供热管网内壁与流通空气之间的热传导系数;hstf为供热管网内壁与保温材料之间的热传导系数;δc为管网平均厚度;δpu为管网侧壁厚度;λc为供热管网内部流通空气的散热值;λpu为管网内部原料的平均温度。
其中,管网内壁与保温材料之间的热传导系数可以通过怒谢尔系数求得,具体计算公式如公式(4)、公式(5)所示[4]。
式中:Nu为怒谢尔系数;Re为流动流体的惯性力与黏滞力之间的比值;Pr为供热网管内部流体热量扩散系数。
通过上述步骤即可计算出城市集中供热管网中的热平衡情况,得到热平衡相关系数,为后续的热平衡调节提供数据基础。
1.2 供热管网换热量计算
在判断完供热管网的热平衡情况后,除了管网内壁与外壁之间交换的热量值以外,还需要计算出管网整体在换热过程中得到的热量,将实际热量与预测温度进行对比,对温度误差进行调节,即可实现对供热管网的热平衡调节,具体实现步骤如下所示[5]。
构建出换热器流出热水与供热管网内部流体之间的换热方程,具体方程表达式如公式(6)、公式(7)所示。
式中:Qi为换热器流出热水对供热管网内部流体传递的热量值;Qj为热水对管网内壁保温材料的散热值;Ki和Kj分别为对应的传热系数以及散热系数;Ai为换热器流出热水与管网内壁之间的接触面积;Δtm为热水与管网内部的平均温差。
其中,传热系数、散热系数主要与管网内部空气对流散热系数有关,具体计算公式如公式(7)、公式(8)所示。
式中:hw为流体侧壁对流散热系数;δi为换热器侧壁厚度;hv为换热器内部空气对流散热系数;δj为加热带平均厚度。
热水与管网内部的平均温差主要和管网内外壁温差的极值有关,具体计算公式如公式(9)所示。
式中:Δtmax和Δtmin分别为管网内外壁温差的最大值与最小值。
对此可计算出供热管网内部交换所得热量,具体计算公式如公式(10)所示。
式中:Qf为供热管网在换热器气阀开启后所得到的热量值。
通过将计算出的实际热量值与热平衡状态下的热量预测值进行对比得到热量差,对热量差进行调节即可实现对供热管网的热平衡调节。该文主要采用供热平衡阀对热量差进行调节。
1.3 自力式流量平衡阀调节
该文通过构建自力式流量平衡阀的方式来对热平衡状态下的供热管网热量预测值与实际值之间的热量误差进行调节,以此解决集中供热管网的水力失调问题,构建出的流量平衡阀结构如图1 所示[6]。
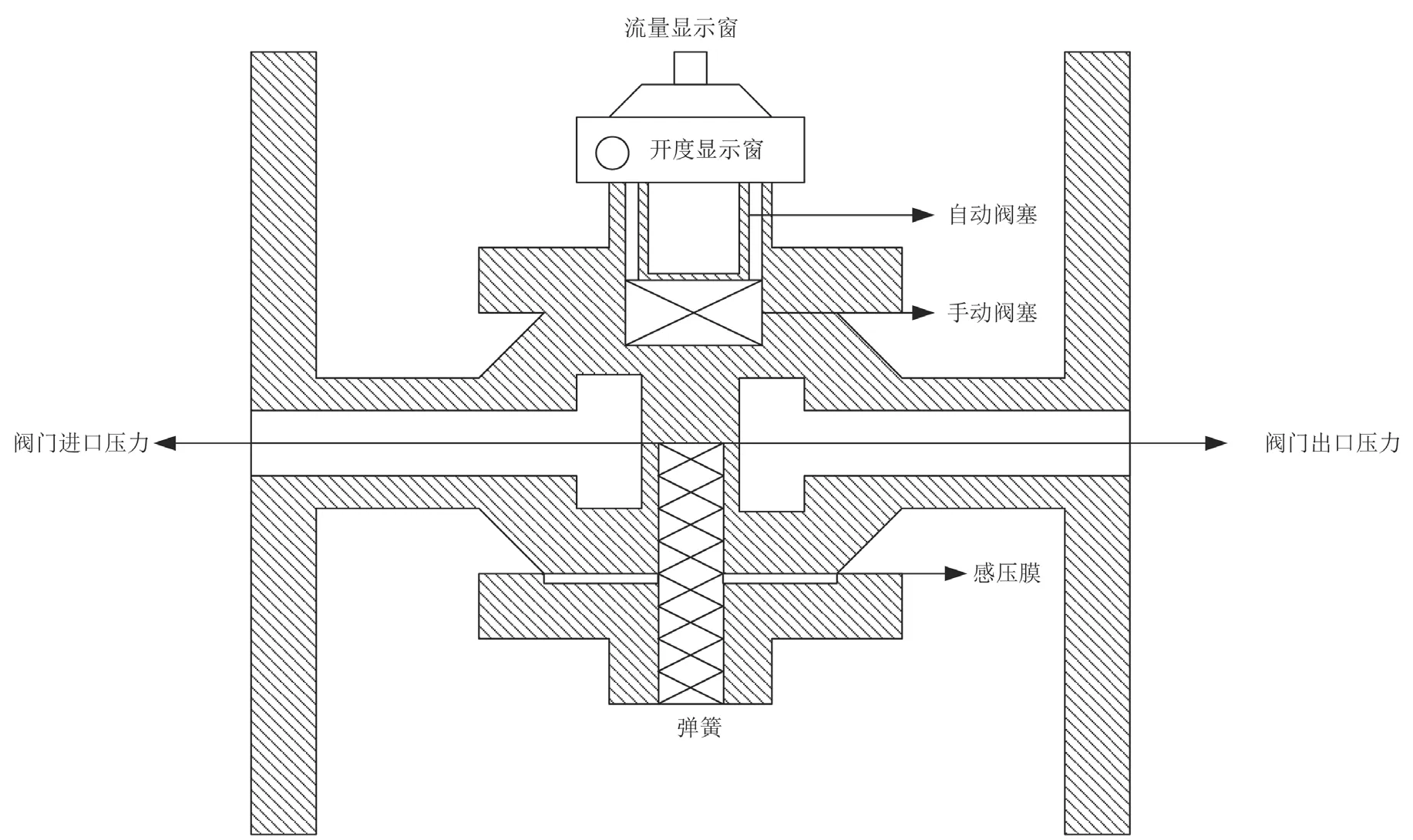
图1 自力式流量平衡阀结构图
本次构建的自力式流量平衡阀主要通过调节阀门进出口的压力实现对供热管网内壁与外壁之间的热量传导。通过在传热过程中给供热管网流体添加局部阻力,进而调节流经换热系统的流量,具体流量方程表达式如公式(11)所示。
式中:Ql为流经自力式流量平衡阀的流量;ζ为自力式流量平衡阀的阻尼系数;P1和P2分别为流体经过平衡阀之前与之后所收到的流量压力;F为自力式流量平衡阀的横截面面积;ρ为流体密度大小;z为阀门流量调节系数。
通过在供热管网的中心部位安装流量平衡阀,对供热系统的流量进行调节,可有效控制供热管网实际得热值,将该值调节到热平衡状态下的热量预测值,即可完成对供热管网热平衡调节[7]。将本节构建的自力式流量平衡阀与上述提出的热平衡状态值、得热量计算相关内容进行结合,城市集中供热管网热平衡调节技术即设计完成。
2 试验部分
为证明提出的城市集中供热管网热平衡调节技术在热平衡调节性能上优于传统的供热管网热平衡调节技术,该文于理论部分设计完成后,构建试验环节,对该供热管网热平衡调节技术的实际热平衡调节性能进行检验与分析。
2.1 试验准备
为提高试验结果的可靠性,本次试验除该文提出的热平衡调节方法外,还选取了2 种常规的热平衡调节方法作为试验对照组,分别为基于垂直单管串联技术的供热管网热平衡调节技术和基于模拟分析法的供热管网热平衡调节技术。
本次试验选取的试验对象为某供热公司供热工程中的一段供热管网。该区域内的供热管网总供热面积为16845.25m2,供热用电负荷为56794.56kW,供热管网内部总体流量为125.46m3/h。换热器出口设计流量压力值为0.165Pa,入口压力值为0.275Pa。供热管网阀门均长期处于全开状态,导致区域内的水力失调情况较为严重。该文通过调用该项目工程的历史数据,得到不同区域下的热用户流量数值,具体见表1。

表1 热用户流量调查表
由上述热用户数据可看出,该区域的热用户实际流量均远低于设计流量,流量失调度较高。因此选用3 种调节方法对该区域的热平衡状态进行调节。本次试验采用MATLAB 仿真软件对热用户流量情况进行建模,将3 种调节方法的参数输入该软件中进行热平衡调节,并对比调节后的失调度数值。
2.2 试验结果
本次试验选取的比较标准为供热管网热平衡调节技术的调节性能,具体衡量标准为不同区域调节后的水力失调度,具体计算公式如公式(1)所示。水力失调度越接近1,代表该区域的热平衡状态表现越好,越能够达到令人满意的供暖效果。本次试验从项目历史数据中随机抽取了5 组区域对其进行仿真调节,具体调节结果如图2 所示。

图2 水力失调度对比结果
有上述试验结果可以看出,对不同区域进行热平衡调节时,不同方法调节过后的区域水力失调度也存在差异。通过数值上的对比可以明显看出,经2 种常规方法调节后的区域的水力失调度有明显下降,但距离1 还是有较大差距。而经该文提出的城市集中供热管网热平衡调节技术调节后的区域的水力失调度明显更接近1,平均调节误差在0.2 左右。由此可看出该文提出的热平衡调节方法的调节性能更强,能够根据不同区域的热用户流量情况进行有效调节,进而减少调节误差。
选用3 种调节方法对该区域热平衡状态进行调节的过程中,耗时是影响调节效率的重要指标,因此对10 个区域进行集中供热管网热平衡调节,将调节耗时定义为从感知到集中供热管网供热不平衡开始直至供热达到平衡这一过程所用的时间,以此检验不同方法的调节效率,比较结果见表2。
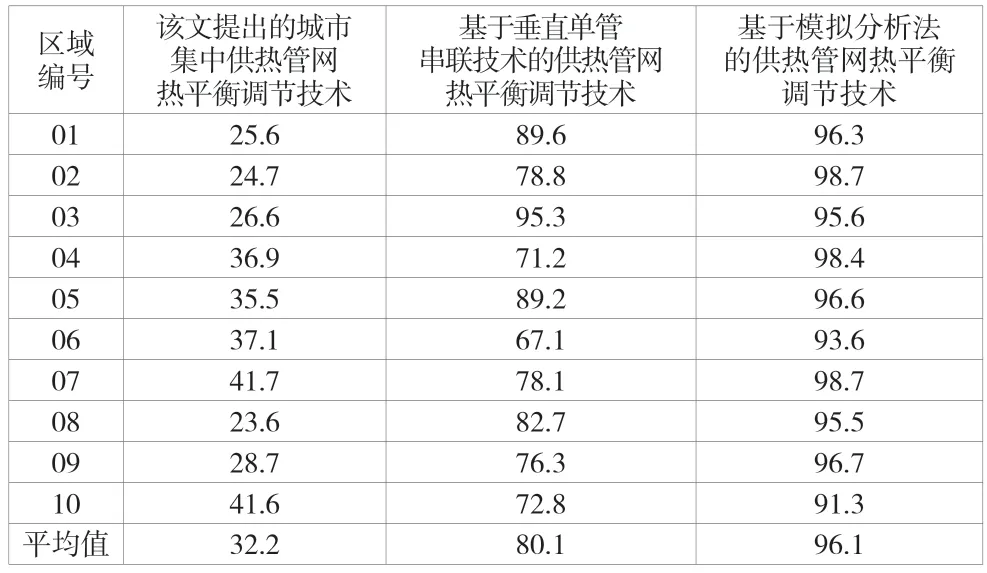
表2 调节耗时比较(单位:min)
通过分析表2 中的数据可知,该文提出的城市集中供热管网热平衡调节技术的调节耗时平均值为32.2min,基于垂直单管串联技术的供热管网热平衡调节技术的调节耗时平均值为80.1min,基于模拟分析法的供热管网热平衡调节技术的调节耗时平均值为96.1min。综合来看,该文技术的调节耗时最短,说明提出的城市集中供热管网热平衡调节技术的执行效率更高,实际应用效果较好。
3 结论
该文提出的城市集中供热管网热平衡调节技术首先对水力失调度进行计算,判定是否需要介入调节。其次通过构建换热方程等手段掌握区域热平衡情况,在此基础上搭建的流量平衡阀调节装置能够有效根据实际需求进行精准调节,具备较好的调节效果。可在满足热用户流量需求的同时对支路流量进行控制,进而降低供热成本,提高区域内的供暖供热水平。
