与三角形角平分线的美丽邂逅

吴岩

最近，我遇到了一个难题。

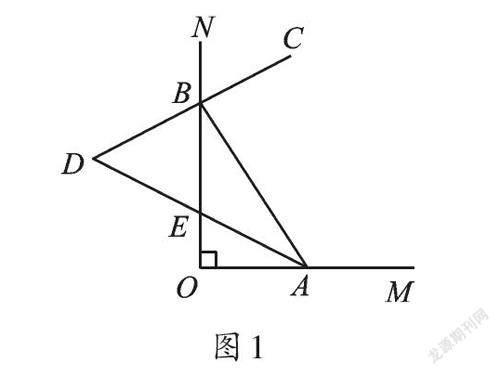
如图1，∠MON=90°，点A、B分别在OM、ON上运动，不与点O重合，BC是∠ABN的角平分线，BC的反向延长线交∠OAB的角平分线于点D，AD交BO于点E。随着点A、B的运动，∠D的大小会变吗？如果不会，请求出∠D的度数；如果会，请说明理由。

读完题目，我有些不知所措。题目中只给出∠O的度数，但是∠D和∠O看起来好像没什么关系啊。

我又读了一遍题目，发现∠NBA是△ABO的外角，再结合三角形内角和定理，可以得到∠NBA=∠O+∠BAO，又因为∠O=90°，所以∠NBA=90°+∠BAO。

还有两个角的角平分线没有用到，角平分线有什么作用呢？哦对了，它能表达三个角之间的数量关系。由AD是∠BAO的角平分线，可知∠BAD=[1/2]∠BAO。因为BC是∠NBA的角平分线，所以∠CBA=[1/2]∠NBA=45°+[1/2]∠BAO=45°+∠BAD。同时，∠CBA也是△ABD的外角，可得∠CBA=∠D+∠BAD，则45°+∠BAD=∠D+∠BAD，从而得到∠D=45°。

我整理了一下思路，写出解答过程：

解：∵∠NBA是△ABO的外角，∠O=90°，

∴∠NBA=∠O+∠BAO=90°+∠BAO。

∵BC是∠NBA的角平分线，

∴∠CBA=[1/2]∠NBA=45°+[1/2]∠BAO。

∵AD是∠BAO的角平分線，

∴∠BAD=[1/2]∠BAO。

∴∠CBA=45°+∠BAD。

∵∠CBA是△ABD的外角，

∴∠CBA=∠D+∠BAD。

∴45°+∠BAD=∠D+∠BAD。

∴∠D=45°。

我的心得：下次我们再遇到类似的题目，首先要明白每个角的身份，即它在三角形中的名称是什么。比如∠D，把它看作△ABD的内角，就可以用三角形内角和找到与∠D关联的角，实现转化。当然，同一个角的身份也可以不同。这时候，我们就可以用不同的方法解决问题了。

比如，BO与AD相交的点为E，那么，∠D也是△BDE的内角，△BDE与△AOE构成对顶三角形，我们可以运用两个对顶三角形的性质来解决。

∠DBO+∠D=∠O+∠OAD，而[1/2]∠NBA=∠NBC=∠DBO，[1/2]∠BAO=∠OAD，∠NBA=∠O+∠BAO……感兴趣的小伙伴可以用这种方法试一试哦。

本题中，点A、B在运动，△AOB的两个锐角在不断改变，三角形的大小也跟着变化，看似无从下手，但变化中含有不变的元素，抓住这个不变量，问题便能得到解决。我想这里也体现了老师常说的几何“变中不变”的魅力吧！

教师点评

求三角形中的角平分线夹角度数是本章中一类常见的数学问题。小作者向我们娓娓道来，从一头雾水到柳暗花明，相信收获的不仅仅是一道题的解法，还有成功的信心和智慧的提升。小作者不仅得出了结果，还给出了分析、解决问题的方法，这样的学习是非常有必要的，也是高效的。善于观察、勤于思考、反思总结是学好数学的法宝。

（指导教师：许 斌）