基于BP神经网络的液体复介电系数反演计算

何春梅，田文艳

(太原科技大学 电子信息工程学院，山西 太原 030024)

0 引 言

随着科技的快速发展，微波能技术几乎应用到了社会生产的各个领域。例如，应用微波能快速加热和烘干[1]、裂解垃圾[2]、食品灭菌[3]以及医学理疗[4]等。这些应用主要依靠介质材料对微波能量的吸收作用。复介电系数作为介质材料的重要电磁参数，常用其表征介质材料对微波能量的吸收情况[5]。因此，在这些应用中，都离不开对介质材料复介电系数的准确测量。同时，研究介质材料的电磁特性对工业材料的发展具有重要意义。相对于传统的固体材料，近年来新兴的液体材料，如室温发光液体材料四苯基乙烯[6]、离子液体电子器件材料[7]等，因其具有绿色环保、功耗低等优点得到了越来越多的关注。液体材料的介电特性也成为人们研究的热点。

近年来，国内许多学者对液体介电特性做出了相关研究。高悦等[8]利用谐振腔微扰法测量蒸馏水和氯化钠溶液的复介电系数，但该方法只能进行窄带测量；刘艳峰等[9]提出一种利用平行板电容器间接测量复介电系数的方法，但该方法仅适用于低频测量；胡敏等[10]利用德拜模型计算得到了不同浓度葡萄糖溶液的介电特性，但该方法计算过程复杂，涉及超越方程求解。以上方法均能在特定条件下实现对液体复介电系数较为准确的测量，但均存在一定的局限。

到目前为止，复介电系数通常采用公式推导计算结合实验测量得到。一般采用各种波导结构(各类谐振腔、微带线、带状线、同轴线等)或者天线系统等得到介质材料的反射、传输系数，并且需要预先计算出介质材料的弛豫模型，最终通过德拜模型或者cole-cole公式计算出待测介质的复介电系数，而这些传统的计算方法涉及超越法方程求解，得到待测介质材料的弛豫模型也比较困难。胡自立等[11]将传统的微波测量技术结合人工神经网络设计了复介电系数反演计算模型。

本文基于文献[11]提出了一种计算复杂度较小且易于实现的BP神经网络反演算法，应用该算法结合同轴探头实现液体的无损测量。同轴探头具有宽频特性，通过时域有限差分法能对同轴探头液体测量结构进行宽频带扫频计算。由于到目前为止，还没有一个明确的公式来描述散射参量与复介电系数之间的关系。BP神经网络具有较强的非线性映射能力，通过对输入输出数据进行多次训练，能够拟合出散射参量与复介电系数间的映射关系，从而得到复介电系数预测网络。通过实验测量待测液体的散射参量，将其输入到训练好的网络中，便可预测出待测液体的复介电系数。因此，通过BP神经网络可反演计算出涵盖大量液体材料的复介电系数。

1 电磁仿真计算与神经网络模型构建

1.1 复介电系数与S11参数对应关系数据集的计算与构建

通过电磁仿真建立计算模型如图1 所示，其中，所用容器是规格为250 ml的玻璃烧杯，烧杯中被测液体体积为100 ml。测量探针为细长同轴探头，其尺寸规格如图2 所示，长度L为200 mm，内导体外直径2a为0.57 mm，外导体内直径2b为1.906 mm，内外导体之间填充材料为聚四氟乙烯。根据同轴探头的结构和传输特性，仿真模式设定为TEM模式，在该模式下设置同轴探头端面馈入功率为1 W。

图1 仿真计算模型

图2 同轴探头长度图与截面图

对复介电系数进行参数扫描，计算出对应参数的幅度值|S11|和相位值φs11。复介电系数[12]

(1)

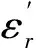
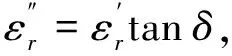
(2)

式中：tanδ为损耗角正切，在复介电系数测量中，一般用损耗角正切表征待测样品溶液在施加电场后其损耗大小的物理量。损耗角正切与复介电系数实部和虚部的关系为

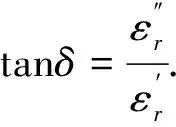
(3)

由于S11幅度值和相位值在不同复介电系数范围内的敏感程度不同，为了进一步提高数据计算的有效性，需要用不同范围复介电系数进行参数扫描计算，梯度具体划分细则及对应计算数据量如表1 所示，其中损耗角正切取值范围为0.05～1。

表1 复介电系数取值步长与取值范围

按照表1 中的复介电系数取值梯度，通过时域有限差分法进行参数扫描后，可以计算出不同复介电系数下对应的S11幅度值和相位值，将表1中仿真计算的4 220组数据按照复介电系数和S11幅度、相位之间一一对应关系，构建用于BP神经网络模型训练和测试的数据集。在4 220组数据中，85%的数据用于训练网络，15%的数据用于测试网络。

1.2 神经网络模型的构建

BP神经网络模型结构简单、数据计算量较小，并且具有较强的非线性映射能力，是目前应用最广泛的人工神经网络模型之一[13]。本文根据复介电系数的特点，设计了两个BP神经网络模型，分别用于复介电系数实部和损耗角正切的反演计算。在每个模型中利用时域有限差分法计算得到的S11幅度值和相位值作为模型输入，将复介电系数实部和损耗角正切分别单独作为输出，构建双输入单输出的非线性映射网络模型。

对于所构建的BP神经网络，隐含层层数和单元节点数是决定网络性能的关键。隐含层层数过多可能会出现网络训练时间变长和训练过拟合的现象，导致网络的泛化性能变差，层数过少则可能造成训练欠拟合，导致网络模型训练不能很好地拟合数据。在对隐含层层数和单元节点数进行多次选择与调整后，最终确定复介电系数实部和损耗角正切的最优参数网络模型分别如图3 和图4 所示。

图3 输出为复介电系数实部网络模型

图4 输出为损耗角正切的神经网络模型

输出为复介电系数实部网络的反演计算[14]公式为

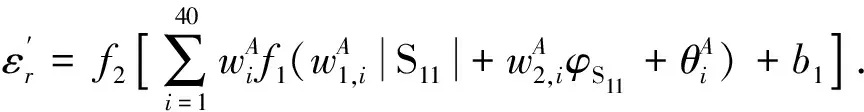
(4)

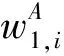
输出为损耗角正切网络的反演计算[14]公式为

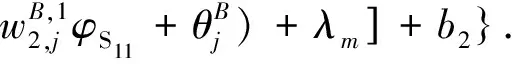
(5)

2 实验测试与结果分析

为了验证输出为复介电系数实部和损耗角正切两个网络的训练性能，对时域有限差分法计算得到的633组测试数据分别在训练好的两个网络模型中进行计算。输出为复介电系数实部测试误差分布如图5 所示，其中，复介电系数实部测试误差主要集中在4%左右。输出为损耗角正切的测试误差分布如图6 所示，其中，仅个别测试值存在偏差，误差主要集中在小于10%的范围内。

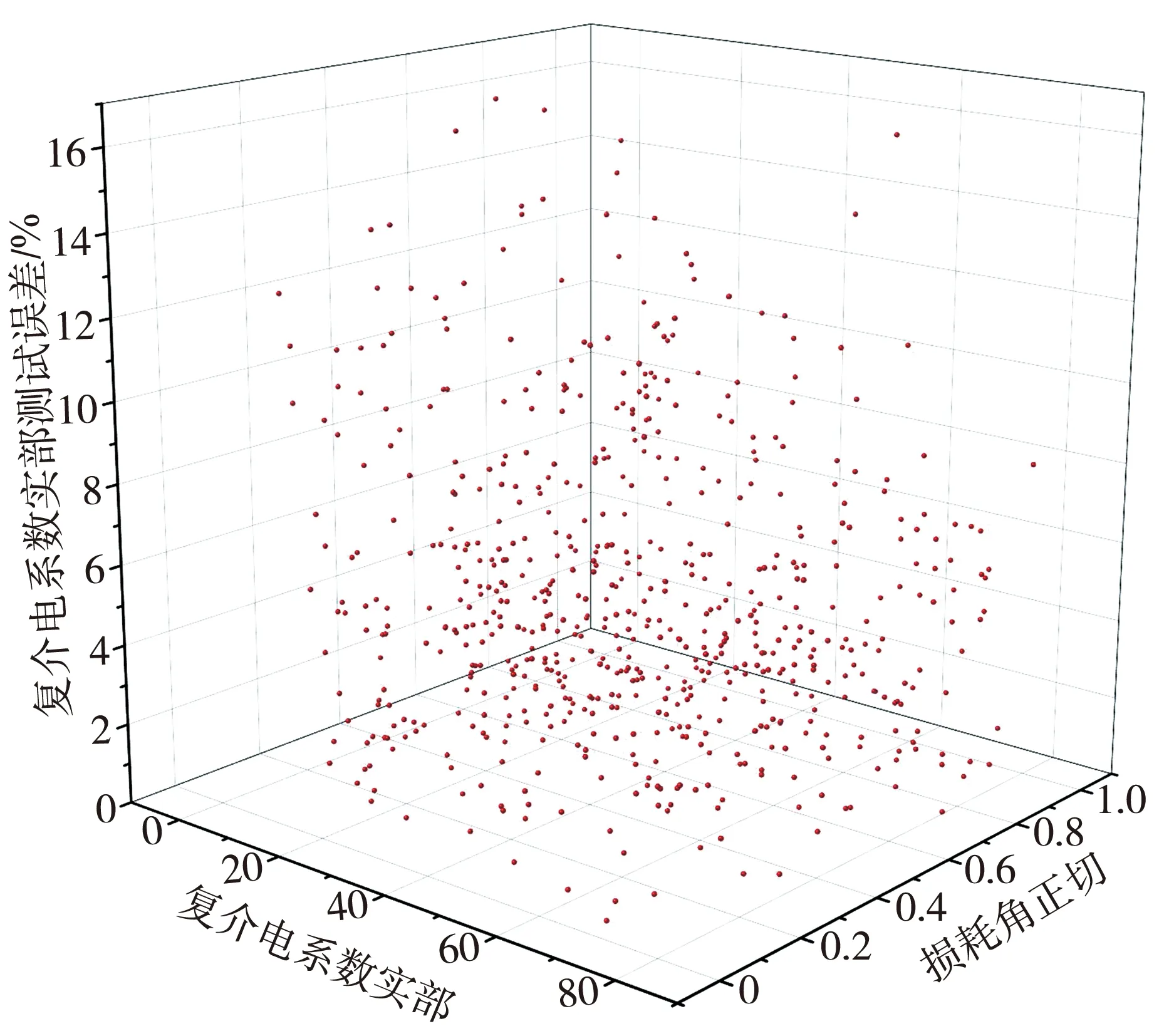
图5 复介电系数实部测试误差

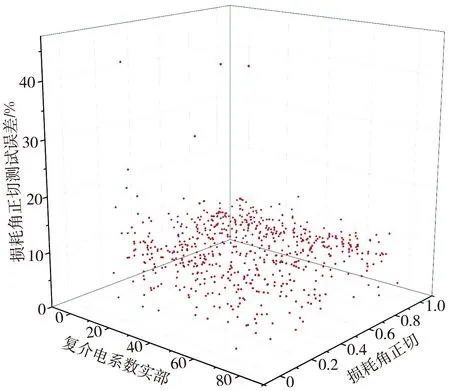
图6 损耗角正切测试误差

通过式(6)计算复介电系数实部和损耗角正切的平均测试误差。

(6)

搭建的实验测量平台如图7 所示。实验所用设备为E5071C型号的矢量网络分析仪，此次实验共对去离子水、二甲基亚砜和无水乙醇3种溶液进行测量。

图7 实验测量图

在实验测量时，3种待测溶液保持20 ℃恒温，矢量网络分析仪频率采样范围设置为2 GHz～3 GHz，步长设置为10 MHz，共101个频率采样点，其中包含仿真计算频率2.45 GHz。此外，为了保证与待测溶液温度的一致性，矢量网络分析仪测量温度同样设置为20 ℃。对矢量网络分析仪进行校准后，在2.45 GHz频率下分别测量3种溶液的幅度值和相位值。对每种待测溶液分别在相同的实验条件下进行多次测量，将测量的平均值构造成用于反演计算的数据集。在对实验测量的数据做同样归一化处理后，通过训练好的网络计算出相应溶液的复介电系数实部值和损耗角正切值。将3种待测溶液的复介电系数实部平均值和损耗角正切平均值与相应文献中的值做比较，计算出反演误差，实验反演计算结果和误差结果如表2 和表3 所示。

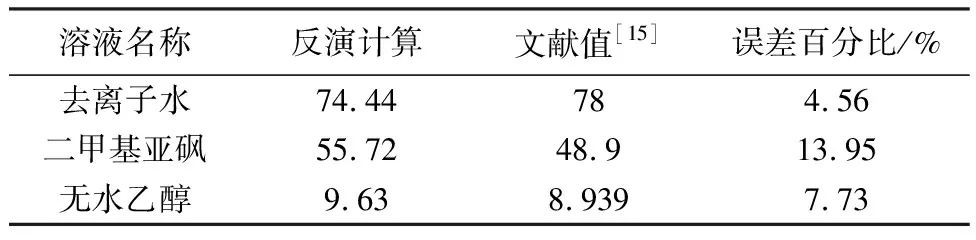
表2 复介电系数实部反演值和误差

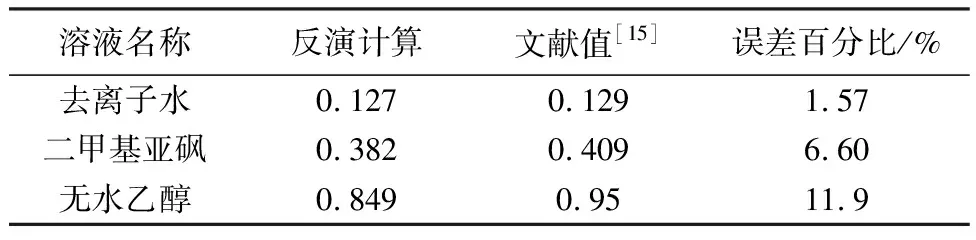
表3 损耗角正切反演值和误差

由表2 和表3 结果可知，实验所测量的3种溶液中，去离子水的反演结果最佳，其复介电系数实部和损耗角正切反演误差均小于5%，二甲基亚砜和无水乙醇相对于物理化学性质较稳定的去离子水，其反演误差相对较大，但3种样品溶液复介电系数实部值与损耗角正切值的反演误差均在可接受误差范围内。实验结果证明了本文构建的复介电系数反演计算模型的有效性。此外，对比文献值，所出现的误差可能来自测量时实际环境温度与所设置的20 ℃标准温度存在一定的偏差，神经网络本身计算时的误差以及所选取训练数据集的样本空间等客观因素。

3 结 论

本文结合同轴探头和深度学习的方法，基于BP神经网络构建了分别用于反演计算液体复介电系数实部和损耗角正切的双输入单输出神经网络模型。首先，通过时域有限差分法计算了2.45 GHz频率下复介电系数实部范围为1～80，损耗角正切范围为0.05～1所对应的S11幅度值和相位值，并构造了复介电系数与S11参数对应关系的训练和测试数据集，通过多次训练和测试得到了复介电系数实部和损耗角正切的最佳网络模型；然后，使用终端开路同轴探头法分别对去离子水、二甲基亚砜和无水乙醇进行了实际测量，得到了3种溶液对应的S11幅度值和相位值；最后，将测量的S11幅度值和相位值代入训练好的网络反演计算出3种待测溶液的有效复介电系数实部值和损耗角正切值。实验结果表明，本文构建的BP神经网络模型反演计算复介电系数的方法有效且较为简单，避免了复杂的高阶推导计算，能够反演计算较大范围介电系数的液体材料，为液体复介电系数反演计算提供了一种可行性思路。