基于改进时间差分的视觉/惯性组合导航研究

王 丰，李 沅，李佳潞，侯 琪，李 皓

(1.中北大学 信息与通信工程学院，太原 030051;2.中国电子科技集团公司第十二研究所 微波电真空器件国家级重点实验室，北京 100015)

0 引言

随着社会的发展，导航越来越成为军事应用、多种地形目标探测和辅助个人定位以及路径规划的核心。在军事上，每个战斗单位的实时定位与多种状态信息对于战场的指挥调度起着至关重要的作用，对于飞弹的准确命中目标也是必不可少的，在陆地单位的战斗中坦克以及驾驶员往往需要较高的位置和状态信息精度以便对战略和路径做出准确的规划。

为了获得更高的精度，现代导航技术往往是采用多种技术如里程计、惯性导航、卫星导航等多种模块组成的组合导航，目前最主流的方法是GNSS与惯性系统的组合导航系统。INS是以经典牛顿力学定律为基础理论的一种可以实现完全自主的导航技术。其根据原理和有无现实的平台可以分为平台式惯性导航系统和捷联式惯性导航系统(SINS，strap-down inertial navigation system)。平台式惯性导航由三轴陀螺仪，三轴加速度计和稳定的平台组成，由平台的三根稳定轴来对一种导航坐标系进行模拟，能够隔离载体自身的角运动，所以其具有精度高的优点。但是同时也由于有平台的存在导致其结构比较复杂，体积较大，制作成本也非常之高，不适用于普通车载。SINS使用虚拟的数学平台代替了真正的平台，使导航系统体积大幅度缩小，集成度大幅提升，成本也大幅度降低，逐渐应用在民用领域，如汽车导航，无人机探测技术，水下探测等领域，但同时也由于其虚拟的数学平台的引入也导致了很多计算上的问题，使得算法更加复杂化，SINS的解算需要用到计算机对加速度计测得的飞行器加速度信号和陀螺仪角速度数据以及当前的姿态信息进行坐标变换，然后再进行INS的计算得出需要的导航状态信息参数。INS的本质是测量加速度与角速度并进行积分运算，其不可避免的问题就是误差随时间的累积导致长时间计算所得AVP信息的不准确不可信[1]。为了克服惯性导导航长航时误差过大的问题，可以采用惯性与多传感器组合的方法来减少误差以便于惯性设备可以更长时间的使用。

GNSS虽具有精度高、实时性好的优点[2]，且GNSS/惯性组合导航也取得了一定的成果，但是在很多情况下几乎无法使用如军事作战、建筑物遮挡与水下、矿洞等[3]，目前国际形势动荡，迫切需要研究在卫星信号不可用情况下的导航与定位。为了实现对惯性误差的补偿，且视觉传感器的低成本和便捷性，越来越多的传感器被使用在导航技术之中，从仿生学导航来说，动物与人类都可以通过视觉和运动的感知来实现对自身的定位导航[4-7]，2014年Martinelli提出了惯性测量单元(IMU，inertial measurement unit)偏置的初始化方法[8]，2017年Scaramuzza等人发现对惯性导航定位和状态信息误差影响最大的是陀螺仪的偏置，而加速度计的偏置影响相对较小[9]，2021年北京邮电大学赵鸿儒、乔秀全等人设计了基于神经网络的视觉惯性里程计提高了载体平移和旋转角度的准确性[10]，2022年火箭军工程大学的薛海建等人提出了一种里程计辅助惯性导航设备定位与状态估计的方法减小了惯性积分误差[11]。本文基于载体运动特点提出一种可靠性较高(判断零速的准确程度远高于视觉实时速度解算)，运算简单的视觉辅助惯性导航进行速度校准抑制误差累积的方法,从而有效减少INS积分的误差累积，便于实现更高精度和更长时间的导航定位和多状态信息的估计[12-16]，可以适用于低精度、低光照和视觉传感器噪声较大的场景，有效的辅助了惯性导航。

1 惯性导航系统

1.1 常用坐标系

1)地心惯性坐标系简称i系，坐标轴相对恒星不变且与地球的自转无关，以地球之心O为原点，其Z轴与地球自转轴重合并以指向北极为正方向，它的X轴指向平均春分点，且指向春分点为正方向，Y轴则是倍定为与X，Z两轴同时垂直且符合右手直角坐标系。

2)地心地固坐标系简称e系，也叫地球坐标系，它以地球质心O为坐标原点，随地球自转而改变，相对于i系旋转角速度为15°/h，Z轴与地球自转轴重合且正方向指向地球北极，X，Y轴在赤道平面内，X轴指向本初子午线，符合右手坐标系。

3)地理坐标系简称g系，随着载体位置的变化而变化，相对载体静止。一般地坐标系有两周表示，即东北天坐标系和北东地坐标系，它们以载体重心为原点O，X轴，Y轴指向当地的东向和北向，在g系中采用经度、纬度和高度来描述载体当前的位置信息。

4)导航坐标系简称n系，一般采用当地的地理坐标系作为导航系。

5)载体坐标系简称b系，主要表现载体的运动方向、运动速度和当前位置等信息，主要载体系有前右下坐标系和右前上坐标系(即载体的X，Y，Z轴正方向分别对应前右下和右前上)分别对应地理坐标系的北东地和东北天。

1.2 坐标系转换

INS载体的姿态信息、速度信息与位置信息的计算需要将载体系输出信息转换到导航系坐标，载体坐标系通过虚拟的数学平台转换到当前的导航坐标系。通过载体当前的姿态信息即航向角ψ、俯仰角θ、横滚角γ，导航坐标系到载体坐标系的转换可以分成3个方向的旋转，整体的转换可以通过一个旋转姿态矩阵来表示(如图1所示)，具体姿态矩阵的计算方法如式(1)所示。

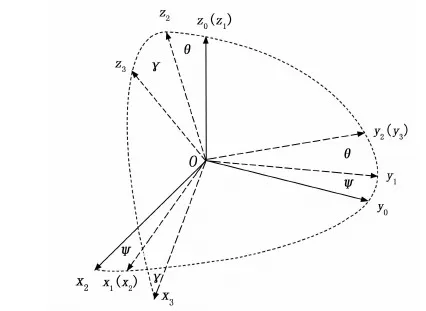
图1 坐标系的旋转

(1)

1.3 INS机械编排

在惯性导航设备工作之前，INS需要先对载体状态信息初始化，初始化的准确度会影响后续的解算误差和精度。初始化主要是指的是对初始位置、初始速度和初始姿态进行初始化对准，惯性导航传感器本身只有初始化初始姿态的能力，而初始速度和初始位置需要GPS给定或者人工设置。初始化之后通过更新算法和IMU加速度计输出的加速度数据和陀螺仪输出的角速度数据进行实时解算与当前状态信息更新，状态信息主要包括姿态信息、速度信息和位置信息，由于不可避免的传感器噪声、精度和力学编排算法具有一定误差的问题，惯性导航的误差会在每一次积分的时候逐渐累积，需要每隔一段时间使用无误差累积的外部观测手段对其进行误差校准，当前最主流的是惯性和GNSS的组合使用，但是在特定场景下GNSS因为遮挡和屏蔽无法使用，我们必须使用他传感器的辅助导航，增强系统鲁棒性，本文采用了视觉传感器与惯性传感器的组合方法。INS的牛顿力学编排原理的基本实现如图2所示。

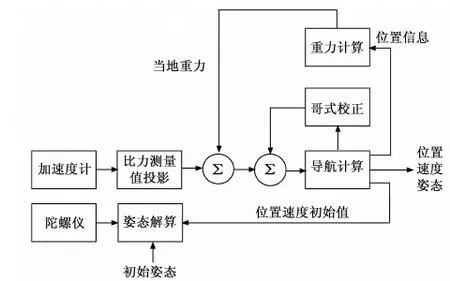
图2 惯性导航力学编排原理

2 差分视觉零速校准

视觉传感器是所有机器视觉信息的源头，其主要是指利用一些光学感应器件和成像结构的组合来获取周围环境的光学信息的仪器，目前视觉传感器的种类和应用日益增加，最常用的有RGB、RGB-D相机、雷达成像和红外成像等，最普通的RGB相机已经广泛的进入到人民的日常生活中[10,17-18]，个人电脑，个人手机以及行车记录仪都有着视觉传感器的身影。惯性导航器件的加速度计与陀螺仪积分运算造成的三向速度不准确以及长时间误差累积较大的缺点，普通视觉里程计需要较高精度和良好的环境才能作为算法正确发挥作用的保障，通常视觉传感器会受到目标物体结构相似、纹理重复以及光照不理想的影响导致的误差较大，不利于准确高精度的辅助惯性系统导航[19]。针对上述的问题，本文利用军事作战单位或者行驶汽车经常驻停的特点提出了使用视觉传感器数据获取当前速度状态并对载体当前速度进行校准，纯惯性导航的核心误差主要有九个，分别为位置误差3个方向的分量、速度误差的3个方向的分量和姿态误差的3个分量，通过速度的校准可以有效的减少速度误差和位置误差。

2.1 RGB相机载体静止判断

视觉传感器记录了相机与世界的相对运动，既可以用于检测相机中运动目标的检测，也可以用来推算相机的运动与否，对传统的惯性导航起到了良好的辅助作用。目前，视觉传感器运动判断最主流的方法通常有3种，分别为光流法，连续帧时间差分法和背景差分法。

1)光流法指的是在连续的两帧图像中由于图像中的视觉传感器自身和视觉场景中物体相对运动导致传感器图像中目标像素的改变。光流法使用的前提是假定相邻两帧之间具有灰度不变性和相邻像素间相似运动，它的理想输出应该是两帧图像中每个像素的运动情况(如图3所示)，并且可以根据算法使用的图像目标像素范围将光流法分成稀疏光流法和稠密光流法。

图3 光流法表示的物体连续运动

由于光流法实现种类较多且计算量较大(最简单的稀疏光流法也需要特征点的计算与判断)，不符合本文要求的计算简单。

2)背景差分法通过背景图像与传感器输入信息进行比较从而分辨出运动的物体，它要求运动物体的像素值与背景的像素值存在较大的差别，需要能够使计算机轻易的区分出运动物体和背景，通过简单的相减便可以得出运动物体的轮廓、形状和大小等信息(如图4所示)，这种方法比较适合摄像机静止的场景，不适用运动中的摄像机，因此不适用本文的研究。

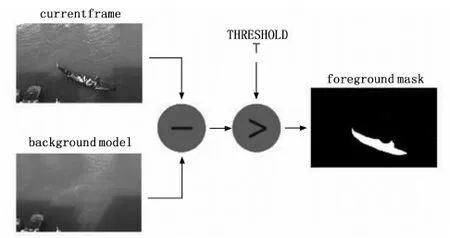
图4 背景差分法计算原理

3)连续帧时间差分法也叫做帧间差分法是一种通过对视频相邻的连续帧做差分运算获取运动目标大小和形状的方法。它根据静止视觉传感器连续帧变化非常微弱的特点来设计的，如果相机静止，那么前后两帧的像素值变化微弱，对这两帧的像素值进行运算，得到的应该是一副纯黑色的图像，由于连续帧时间差分法对光线等场景变化不敏感，能适应多种不同的复杂环境，鲁棒性较高并且计算量最小，原理简单，能够最准确、最快速的判断出载体的运动与静止状态，所以本文采用此种方法并对其进行适当的算法改进以便于外界信息的观测与使用。

2.2 改进连续帧时间差分法

相机连续两帧时间差分是一种较为常用的的相机静止判定方法，只需要选取视觉传感器输入的时间上的前后两帧进行运算即可得到相机的运动静止信息，其可以用于检测运动物体，对与动态的物体有很强的自适应性[20]，也可以用于检测相机本身的运动，相比传统视觉里程计计算更为简单且零速误差极小(连续帧差分法的像素级运算)，只需要检测的光源信息具有一定区分度即可，无需较好的光源和高精度的传感器，具有更大的速度参考价值，主要流程如图5所示。

图5 静止判断流程图

对于某些视觉传感器分辨率较高，得到的是很多分辨率较高的图像，数据图像的长度和宽度过大导致的计算量巨大且运算速度慢，因为使用连续帧时间差分的方法运算数据量较大，为了减少像素的差值运算量，由于本文研究不需要获取运动目标的清晰轮廓，所以可以通过采用间隔取点运算的方法进行差分运算，这种方法基本不会影响其判定运算的结果，但是却可以节约大量的运算成本。例如，对于一幅1 000*1 000的高分辨率RGB图像，时间差分计算至少需要3*1 000*1 000次运算，而采用每隔10个点进行采样计算的情况下计算量为3*100*100，运算量足足减少100倍，对于某些帧率过高的视觉传感器输入，可以采取关键帧的策略，即每间隔一定的时间或帧数来选取需要解算的帧作为关键帧，也可以大幅减少运算耗时，具体间隔时间和帧数应当根据具体的要求来确定，以便在获取足够高的精度的同时减少计算量。图6为每5个像素选取一个关键像素点信息进行差分计算的原理示意图。

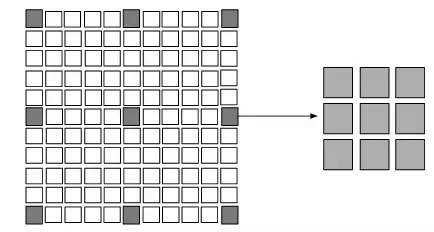
图6 间隔采用示意图

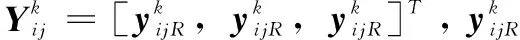
图7 采样像素点做差运算

(2)

(3)

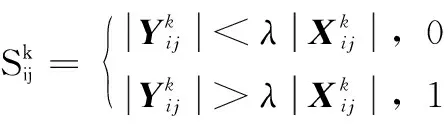
(4)

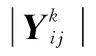
(5)

T为采样点位置像素不变的指标，范围为[0，1] ，我们可以根据需求设定一个合适阈值来屏蔽图像中运动物体造成的影响，当T大于所设阈值时可以定为载体静止，如果阈值设置太小，无法抑制差分图像中的噪声，设置过大则会导致运动信息的误判。设定阈值的优点在于对运动目标干扰有较强的鲁棒性，T值越接近1，则对载体的静止置信度越高，由于使用时间差分法对载体的静止进行判断，误差级别属于像素级，判断结果有较高的可靠性和可信度。

3 扩展卡尔曼滤波信息融合

多传感器信息融合相关的研究开始于20世纪的80年代。多传感器融合的常用方法有:加权平均法、统计决策、卡尔曼滤波和神经网络等方法。加权平均的方法虽然是最简单、最直接的办法，但是它的理论结果不符合统计学的最优估计理论且只适用于低动态水平的数据处理;统计决策理论多用在多个传感器融合相同种类的数据，一般只用于图像的观测数据信息;对于系统状态的噪声和观测值的噪声为高斯白噪声或者近似相当于高斯白噪声的线性系统模型可以采用卡尔曼滤波的方法来融合动态冗余的多传感信息，对于非线性系统模型采用扩展卡尔曼滤波或者无迹卡尔曼滤波，扩展卡尔曼滤波通过非线性当前时刻值的一阶泰勒展开式来表示其线性状态以此将其线性化以便于符合卡尔曼滤波的基本条件，而无迹卡尔曼滤波则是通过对状态输入的选值运算来求取函数的均值和协方差矩阵，这样做可以避免扩展卡尔曼滤波泰勒展开计算雅可比矩阵运算量巨大的问题;而基于神经网络的方法根据系统模型和应求的解，通过一定的神经网络结构对和损失函数对结果进行评价并进行非线性优化来学习确定各个网络连接的权值，对各个传感器的输入信息进行融合，由于神经网络内部的黑盒特性，通常无法对其进行精确的解释，且很容易陷入局部最优化的问题，目前也是一个研究的热门方向之一。

卡尔曼滤波是一种通过利用线性系统状态方程，并通过系统输入观测实时数据，以此对下一时刻系统状态进行最优估计的算法。由于其观测数据中包括了线性系统中符合高斯模型噪声和干扰的影响，所以最优估计的过程也可被看作是一种滤波过程，也可以称为卡尔曼滤波器。它最初用于阿波罗计划的导航电脑，是随机系统实时最优估计估计问题的唯一实际的有限维解决方法，它设计的概率分布只需要做出很少的假设，只需要状态方程含有有限的均值和协方差。目前卡尔曼滤波应用的主要目的一般分为两种，即估计动态系统的状态信息和估计系统的性能分析。

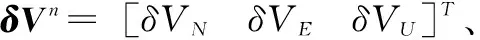
(6)

Zk=HkXk+Vk

(7)

(8)

(9)

(10)

(11)

(12)

Pk=(I+KkHk)Pk/k-1

(13)

我们需要提前确定并输入P，Q，R矩阵，初始值的设置应该是初始状态信息、惯性系统的噪声和量测方程的噪声方差阵。具体原理和流程如图8所示。

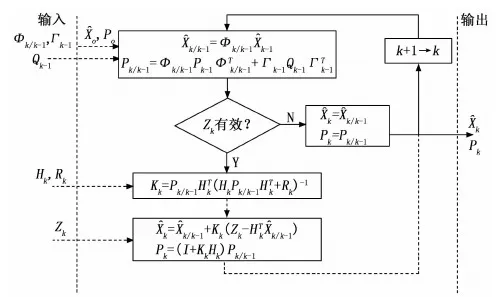
图8 卡尔曼滤波估计流程图

4 仿真实验与分析

4.1 仿真实验设置

图9 视觉/SINS组合导航系统结构

4.2 仿真结果与分析

仿真数据在载体运动期间一共设置了三次短时间驻停用以给视觉传感器做驻停判断并以扩展卡尔曼滤波融合的方式校准惯性导航推算的载体三向速度。仿真实验设置的真实的AVP信息如图10～13所示。

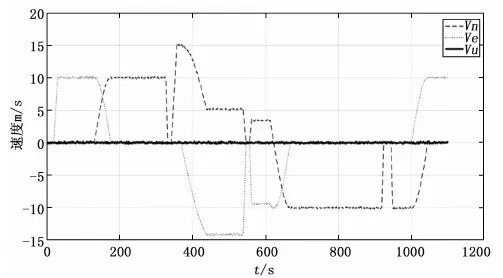
图10 载体三向速度

图11 载体俯仰角和横滚角

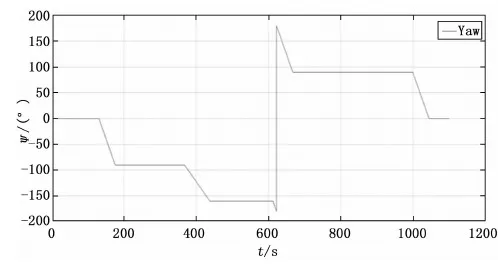
图12 载体航向角

4.2.1 行驶轨迹对比分析

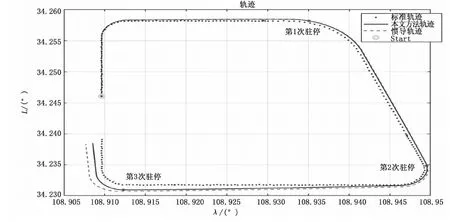
图14 载体行驶轨迹

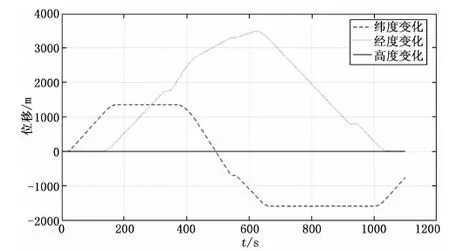
图13 载体经纬高变化

经过载体零速校准信息进行校准后，多种导航方法的轨迹对比如图14所示，标准轨迹为仿真的GPS位置数据添加3 m的高斯位置误差，与纯惯导相比载体运行轨迹更加接近真实的轨迹，证明运行时间越长与纯惯性导航的轨迹相差越大，有效的抑制了惯性导航定位误差随时间的发散，证明本文方法的有效性。其位置的东向和北向位置误差在全局上比纯惯性导航的表现更加接近优秀，如图15～16所示。

4.2.2 RMSE误差分析

均方根误差(RMSE,root mean square error)是导航研究领域的一种比较常用的误差评价标准，RMSE可以反映出测量数据偏离真实值的程度，数值越小表示测量值越接近真实值，测量精度越高。本文以位置的RMSE作为其北向和东向位置误差的评价标准，其计算结果如表1所示。显然，本文的方法从误差结果上要更加优于纯惯性导航，RMSE在北向位置上减少了19.0%，在东向误差上减少了32.1%，证明了视觉对惯性导航校准和抑制误差发散的有效性。

(14)

5 结束语

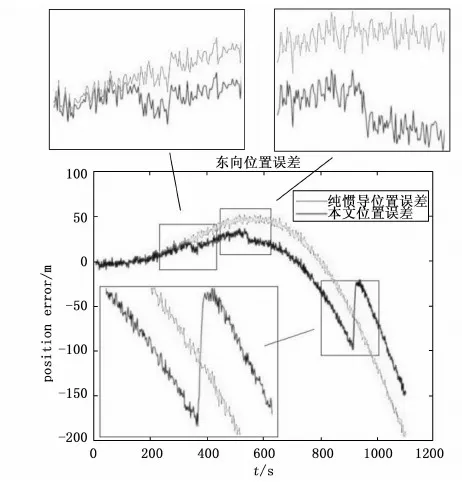
图15 东向位置误差

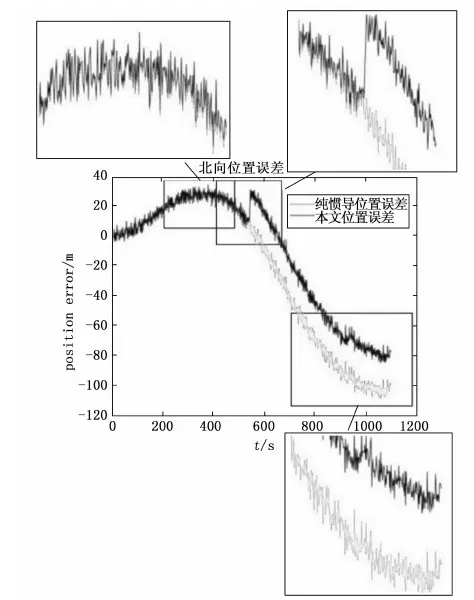
图16 北向位置误差

由于惯性导航的姿态，速度和位置误差随时间发散，需要每隔一定的时间对其进行校准，本文根据汽车和一些军事作战载体具有经常驻停的特性使用视觉进行判断速度并校准，本文方法对视觉传感器要求低(无需高质量图像和良好的光源环境)，鲁棒性高，可以更加稳定高精度的辅助惯性导航设备，计算简单快捷能够满足实时解算，并且可以有效抑制惯性导航的误差发散，使其定位与速度状态信息更加具有参考性，提升了在特定条件下GNSS信号不可用的惯性导航性能，是一种有效的导航误差解决方案。惯性导航的姿态误差是一种影响较大的误差，未来研究应加入位置校准和偏振光航向角对姿态进行校准，提升惯性导航在长时间上使用的性能。