基于六边形网格组部署的对称密钥预分配模型
2023-04-03庞浩杰
庞浩杰 ,常 凯 , 金 琰, 朱 亮
(1.河南省洛阳正骨医院(河南省骨科医院), 郑州 450016; 2.湖北中医药大学 信息工程学院,武汉 430065;3.郑州轻工业大学 计算机与通讯工程学院,郑州 450002)
0 引言
传感器网络有许多应用,如家庭安全监控、军事侦察、环境监测和目标跟踪等等[1-4]。典型的传感器网络通常由大量的微小感知设备构成,这些设备又称为传感器节点,它们的电池电量和数据处理能力有限,并且通常通过短距离无线电信号彼此通信;在许多应用中,传感器节点通常随机分布在特定区域,以感知和收集有用的信息。
传感器网络最基本的安全要求之一是保证传感器节点间发送信息的保密性和完整性。尤其是传感器网络部署在“敌对”环境中时,密钥的建立在认证和加密中起着很重要的作用。攻击者可以通过对传感器节点发起物理攻击,或者对不同的通信协议采用逻辑攻击来窃听消息或使网络失效[5-6]。因此,传感器网络需要加密和认证服务。由于资源的限制,实现有效的密钥建立机制并不是一项简单的任务。除了目前流行的椭圆曲线密码体制外[7],对称密钥算法[8]也是解决这一问题的可行途径。
文献[9]提出的随机密钥预分配模型离线生成一个大的密钥池,每个传感器从密钥池中随机选取一个密钥子集。通信范围内的任意两个节点只有共享一个公用密钥才能相互通信。根据密钥池的大小和网络中传感器节点的数量,这种体制可以实现不同的连通性和恢复能力;文献[10]提出将部署知识应用到基本的随机成对密钥中;文献[11]通过应用部署知识提出了一种密钥预分配模型。在这种模型中,把整个网络分成组,每个组执行基本的随机密钥预分配。一个组的密钥池与水平组密钥池共享(个密钥,与对角组密钥池共享(个密钥;从Blom解决方案[12]发展而来的密钥矩阵方案还有文献[13]的多空间密钥预分配模型。
文献[14]提出了采用多项式的随机密钥生成思想。它采用对称多项式计算来获得成对密钥。这种方案对捕获的节点具有t-串谋抵抗能力,即小于t+1个节点的攻击不会泄露任何关于其他节点密钥的信息;文献[15]基于该思想和基本随机密钥预分配[9],提出了随机子集分配密钥预分配模型。与生成大型密钥池和创建密钥环不同,该方案创建一个大型多项式池,并从池中为每个节点分配一个多项式子集。这样,两个节点只有共享至少一个公用多项式才能相互通信。结果表明,与文献[9]模型相比,这种模型提高了恢复能力;文献[16]提出了利用预部署知识的私有多项式预分配方案,文献[17]提出了基于8-方形网格的多项式预分配方案;文献[18] 针对Sheetal Kalra 方案容易在数据库泄露和用户智能卡丢失的情况下受到用户的假冒攻击、并且不能达成正确的共享密钥的分析,基于口令的无线传感器网络认证方案,提出了一种改进的带有智能卡的认证方案,解决了 Sheetal Kalra 方案中的安全性问题,提供了用户、传感器、网关节点之间的相互认证并达成正确的共享密钥。此外,还给出了提出方案的安全性分析,以此证明提出的方案可以满足无线传感器网络中的安全需求;文献[19]针对移动异构无线传感器网络模型,提出了在一种安全高效的密钥管理方法。方法采用椭圆曲线密码学加密算法实现移动节点位置信息到基站的安全上传,以及基于密钥哈希的消息认证码来实现消息源的身份认证。基站则对收集的移动节点位置信息进行统计分析来协助完成固定节点与移动节点间的身份认证及会话密钥建立。实验结果表明,所提出的方法在密钥建立过程中节省了网络资源,同时可有效防御攻击者发起重放攻击,节点复制攻击和女巫攻击等,增强了网络的安全性;文献[20]基于具有节点移动性的动态传感器网络安全通信,分析了一种证书无效密钥管理(CL-EKM,certificate less-effective key management)协议,保护数据和通信需要适当的加密密钥协议。针对具有节点移动性的动态传感器网络的安全通信,提出了一种证书无效密钥管理(CL-EKM)协议。CL-EKM协议支持在节点离开或加入集群时进行高效的密钥更新,并保证了向前和向后的密钥保密。该协议还支持对被破坏的节点有效的密钥撤销,并将节点被破坏对其他通信链路安全的影响降到最低。对方案的安全性分析表明,该方案能够有效地防御各种攻击。
上述这些解决方案在采用预部署知识来提高性能和安全性方面仍有一些局限性。对此,本文提出了一种基于六边形网格组部署的无线传感器网络对称密钥预分配模型。模型将多项式信息分配到一个六边形网格组中的特定区域内有限数量的传感器节点上,从而使得每个传感器节点找到与其相邻节点的共享密钥空间;仿真实验结果表明,提出的对称密钥预分配模型不仅具有良好的加密性能,而且相比于其他模型的密钥方案有更好的内存开销、运行时间和节点受损攻击时的网络恢复能力。
1 相关模型
1.1 基于Blom思想的密钥预分配模型
基于Blom思想提出的密钥预分配模型[9]能够确保组中的任何一对成员都可以计算公用共享密钥。用N表示网络中传感器节点数目,G为有限域上大小为(t+1)×N的生成矩阵,D为大小为(t+1)×(t+1)的秘密随机矩阵,其中t为攻击者攻击的节点个数。从矩阵G和D,构造一个N×N的对称矩阵K,它的元素是节点之间的成对密钥,则矩阵K为:
K=(D·G)T·G
(1)
每个节点i存储私有矩阵A=(D·G)T对应的第i行。如果节点i想要与节点j通信,则它计算其存储的行向量与G的第j列的内积,得到公用密钥Ki,j。文献[13]的多空间密钥预分配模型将Blom思想与文献[9]的基本随机密钥预分配模型相结合应用于传感器网络。在这种方法中,他们将每个元组(D,G)生成的密钥空间表示为密钥集合。网络中的每个节点随机存储来自于ω个预生成空间的τ个空间。基于概率,任意两个节点可以共享一个公用空间,该空间可以计算出一个公用秘密密钥。所有密钥矩阵解决方案都具有阈值t-安全特性,即当攻击者攻击的节点不超过t个时,未被攻击的节点之间的通信仍然是安全的。
1.2 基于Blundo思想的密钥预分配模型
基于Blundo思想提出的多项式密钥预分配模型[15]采用对称多项式计算来获得成对密钥,方案使用n个变量的t次多项式来建立t-安全n-联盟的密钥分配。应用于两个对象之间的成对密钥,密钥预分配服务器在一个有限域Fq上随机生成一个二元t次多项式:
(2)
其中:q是一个足够大的素数,可以容纳一个密码密钥,函数f(x,y)是对称的即f(x,y)=f(y,x)。每个节点有唯一的整数IDi,加载来自于多项式f(x,y)的信息f(i,y)。这样,任意两个节点i和j可以计算节点i的密钥Ki,j=f(i,j)和节点j的密钥Kj,i=f(j,i)。由于对称特性,有:
Ki,j=Kj,i
(3)
故两个节点有一个共用的成对密钥。
每个节点必须存储t+1个系数,每个系数有log2q比特(bits)。因此,该模型中每个节点的内存存储需求为(t+1)log2q比特。由于存储密钥的内存开销很大,这种方案不能直接应用于传感器网络,因为内存的大小按指数规律依赖于网络的规模,因此对于资源受限的传感器节点等设备来说是不可行的;对此,本文将通过采用预部署知识来解决这个问题,并表明相比其他基于多项式的、应用预期位置知识的方案更具优势;此外,我们在计算成对密钥中还加入了一些随机数,这样,对手就很难对未捕获节点的额外安全连接造成破坏。
2 基于六边形网格组部署的对称密钥预分配模型
在提出本文方案之前,我们将密钥空间定义为采用Blundo模型生成的一个t次二元多项式f(x,y)的全部密钥的集合,密钥空间中的密钥数量表示密钥空间大小。假设如果一个节点携带f(x,y)生成的信息,则它将选择一个密钥空间。任意两个选择公用密钥空间的节点总是计算它们的成对密钥。
节点nA选择密钥空间fu,v(x,y),如果它携带fu,v(nA⊕RvA,y)的系数,其中RvA是节点nA的随机值,将在密钥预分配阶段进行描述。当两个节点在相同的密钥空间时,它们可以计算成对密钥来建立安全通道。
本文方案允许传感器节点在部署后找到与其相邻的每个节点的公用密钥空间。方案共分为3个阶段:密钥预分配阶段、直接密钥建立阶段和间接密钥建立阶段。在部署前执行密钥预分配阶段,将凭证信息预加载到每个传感器节点。之后,如果两个传感器节点至少共享一个共用密钥空间,则可在它们之间建立一个直接密钥,否则,它们可以在间接密钥建立阶段的基础上商定一个间接密钥。
首先,要解决传感器网络的部署模型。
2.1 基于六边形网格组的传感器节点部署
在本文模型中,把目标区域划分为六边形网格。六边形网格提供了对圆的最佳近似,比在连续区域中可以重复使用的其他2种几何图形(三角形和矩形)所覆盖的面积更大。与矩形的8个或三角形的12个相邻单元格相比,六边形有最少的相邻单元格(6个)。传感器节点在单元格上进行划分并分组。这种模型适合于实际场景,当每组的传感器节点一起部署时,预期的相邻组更有可能彼此接近。
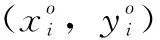
(4)
式中,(xi,yi)为组Gi中的节点ni的坐标,σ为分布的标准偏差。基于六边形网格组的部署模型如图1所示。
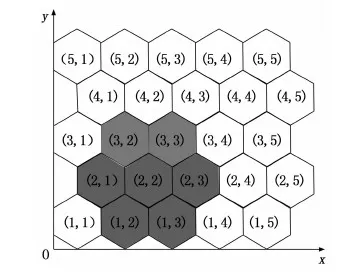
图1 基于六边形网格组的部署模型
在描述本文方案的原理之前,定义集群为3个相邻组的集合,一个组有3种类型的集群:1-集群、2-集群和3-集群。对于任何一个组(i,j),1-集群包含这个组(i,j)和组(i+1,j)以及(i+1,j+1),2-集群包含这个组(i,j)和组(i,j-1)以及(i-1,j),3-集群包含这个组(i,j)和组(i-1,j+1)以及(i,j+1)。
例如在图1中,对于组(2,2)来说,组(3,2)和组(3,3)属于1-集群(2,2),组(2,1)和组(1,2)属于2-集群(2,2),组(2,3)和组(1,3)属于3-集群(2,2)。
在一个单元格上,分布函数可能是不均匀的,但可以在部署点之间选择合适的距离,使得总体分布接近均匀。
2.2 密钥预分配阶段
此阶段的目标是将密钥材料分配给每个节点。基于这些密钥材料,相邻节点在部署后可以对密钥进行配对设置。
这个任务是通过离线服务器完成的。首先,服务器为每个集群生成一个多项式池F,它包含足够多的t次对称二元多项式。然后将每个多项式分配给每个集群中的所有传感器节点。由于每个单元格属于3个集群,所以每个节点要存储3个t次二元多项式的知识。换句话说,每个节点要选择3个密钥空间。算法1所示为多项式预分配实现的伪代码。
这一阶段完成后,每个传感器节点存储一个节点ID、3个空间ID、一个随机值和3个对应于3个密钥空间的系数向量的值。这些密钥材料将用于下一阶段的成对钥匙建立。
算法1:多项式预分配算法
Input: 网络中的节点集合N, 集群集合Ψ, 多项式池F
Output: 加载密钥材料给网络中的每个传感器节点
1.For每个组Gi,j
2.For1-集群(Gi,j)中的每个组Gu,v
3.If不在polynomial_sharing(Gu,v,Gi,j)中
4.生成一个f(x,y)
5.把f(x,y)分配给1-集群(Gi,j)
6.Endif
7.Endfor
8.For2-集群(Gi,j)中的每个组Gu,v
9.If不在polynomial_sharing(Gu,v,Gi,j)中
10.生成一个f(x,y)
11.把f(x,y)分配给2-集群(Gi,j)
12.Endif
13.Endfor
14.For3-集群(Gi,j)中的每个组Gu,v
15.If不在polynomial_sharing(Gu,v, Gi,j)中
16. 生成一个f(x,y)
17. 把f(x,y)分配给3-集群(Gi,j)
18.Endif
19.Endfor
20.Endfor
2.3 直接密钥建立阶段
在传感器节点部署到目标区域后,每个传感器节点必须找到与其相邻节点的共享密钥空间。假设节点nA具有3个空间IDfi,fj,fk,需要与其邻居发现共享密钥空间。它广播一个1-跳发现消息—密钥空间发现消息(KSDM,key-space discovery message)如下:
(nA,RvA,H(fi⊕RvA),H(fj⊕RvA),H(fk⊕RvA))
(5)
式中,H为哈希函数,⊕为异或运算。
当A的一个邻居(设为B)接收到这个消息时,它会发现它可以与A共享3个、1个或不共享公用密钥空间。类似地,节点A也接收到B的KSDM消息并发现公用密钥空间。如果共享至少1个公用密钥空间,则B和A之间的成对密钥在B点计算如下:
KB,A=f(nB⊕(RvB,nA⊕RvA)
(6)
在获得KB,A之后,节点B从它的内存中删除RvA值。计算A点的成对密钥的过程与此类似。由于二元多项式的对称性,所以:
KA,B=KB,A
(7)
完成这一阶段后,除了前一阶段的密钥空间信息和一个随机值外,每个节点还存储一个与其相邻节点的成对密钥列表。
2.4 间接密钥建立阶段
如果两个相邻节点之间没有公用密钥空间,则需要通过一个或多个中间节点建立一个路径密钥,实现过程如下。
在直接密钥建立阶段之后,每个节点A知道其安全邻接节点的集合SA。源节点A希望与其邻居B建立一个成对密钥,但是B和A不共享任何密钥空间。在这种情况下,A生成一个会话密钥KS,并找到在SA中与节点B有相同的组ID或包含节点B的组的相邻组ID的节点C,然后节点A向节点C发送一条包含通过密钥KA,C加密的KS消息。然后,节点C通过密钥KC,B保护的安全通道向B发送会话密钥,则密钥KS作为节点A和节点B之间的成对密钥。
在以上3个阶段完成之后,每个节点都存储一个包含邻居的IDs和对等的密钥表。密钥材料的存在使得传感器网络能够增加新的节点供后面替换。
2.5 传感器节点的添加和删除
为了增加一个新的传感器节点,密钥建立服务器只需要将相关的多项式共享预先分配给新节点,类似于预分配阶段。由于密钥空间的大小是有限的,添加的传感器越多,该单元中的安全性就越低;删除方法很简单。每个传感器节点只需要存储一个与自身共享至少一个二元变量多项式的被破坏传感器的黑名单IDs。如果有超过t个被破坏节点共享同一个多项式,则拥有该多项式的非被破坏节点将删除该多项式和所有相关的被破坏节点。
算法2为密钥建立和分配实现的伪代码。
算法2:密钥建立和分配算法
1.ForN中每个传感器节点nADo
2. 对nA的预加载数据生成并插入一个随机值RvA;
3.Endfor
4.For(中每个集群CiDo
5.从F中获取一个二元多项式fi(x,y);
6.ForCi中每个节点nADo
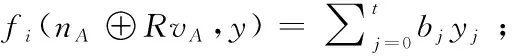
8. 插入nA的预加载数据{bj|j=0,...,t};
9. 将多项式的ID(也称为了空间-ID)fi插入到nA;
10.Endfor
11.从F中删除fi(x,y);
12.Endfor
3 算法仿真实验结果及分析
仿真中采用的度量指标如下。
1)网络连通性:包括局部连通性和全局连通性。局部连通性是指一个节点可以在其传输范围内与相邻节点连接的概率。全局连通性是最终密钥图G中形成最大独立连通部分的传感器节点数目与整个网络的大小之比。
2)内存开销和运行时间:内存开销为模型中在节点上存储密钥材料的内存需求,运行时间为密钥空间形成和分配,直至最终两个节点获得成对密钥所消耗的时间。
3)对捕获节点攻击的恢复能力:对手通常发起节点捕获攻击,以窃听网络中的安全通道,或者利用捕获节点泄露的密钥材料进行节点复制攻击。在此分析中,我们评价节点破坏攻击对剩余网络通信的影响,即对手能够发现一个二元多项式的概率,这意味着它们可以泄露所有由这个多项式得到的加密安全连接。
3.1 系统配置
采用表1中的设置进行仿真和数值分析。在这种场景下,假设节点部署遵循二维高斯分布,其PDF函数如式(1)所示。
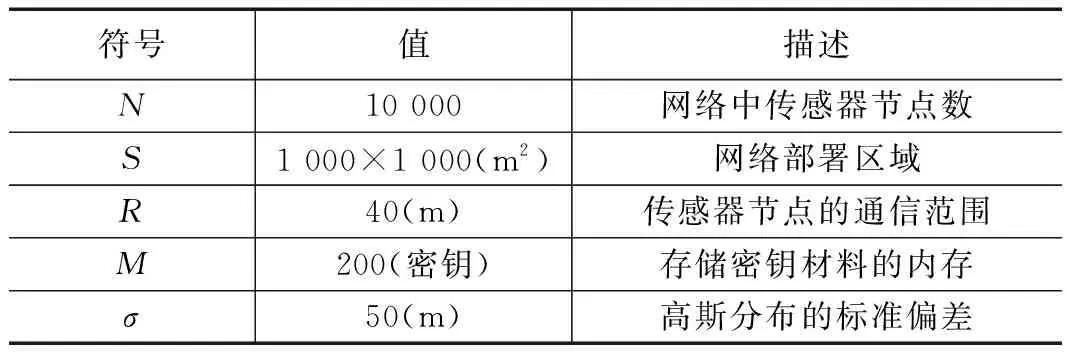
表1 仿真设置
3.2 网络连通性
假设A(ni,nj)和B(ni,nj)为事件,节点ni为节点nj的邻居,它们共享至少1个共用密钥空间。局部连通性可以计算为:
Plocal=P(B(ni,nj)|A(ni,nj))=
(8)
节点ni∈Gi为节点nj(xj,yj)的邻居的概率是在节点nj周围半径为R的圆上的PDFf(ni)的积分:
(9)
由于nj按式(1)分布在组Gj中,所以ni∈Gi为nj∈Gj的邻居的概率为:
(10)
因此:
(11)
用S(Gi)表示Gi相邻组的集合,则有:
(12)
由于传感器节点是在给定的组中以相等的概率被选择的,因此局部连通性可以计算为:
(13)
用d=k×σ表示两个相邻单元格的两个部署点之间的距离(k为比例系数),这个值会影响网络的局部连通性和全局连通性。当k值较大时,则一个组中几乎每个节点都位于自己的单元格区域内,而且相邻节点都来自自己的组。在这种情况下,局部连通性非常高,但网络完全被分割成单独的部分,这意味着全局连通性非常低;当d值较小时,可能局部连通性较低,但全局连通性较高。因此,选择合适的d值会影响网络的连通性。由于无线传感器网络中密钥建立的最终目标是形成尽可能高的全局连通性网络,因此必须适当选择相邻部署点的距离d的值。
表2所示为通过改变k来得到不同的d值获得的局部连通性和全局连通性。可以看到,当两个相邻单元格的两个部署点之间的距离过小(k=0.4,0.6,0.8或1.0)时,在任意节点A,其周围分布着许多非相邻单元格的节点,这些节点不与节点A共享任何密钥空间,因此降低了局部连通性和全局连通性;而当选择合适的部署点距离值时,模型能够获得较高的局部和全局连通性,如当k=1.5时,全局连通性为0.999 0,即网络中只有0.01%的节点是浪费的。
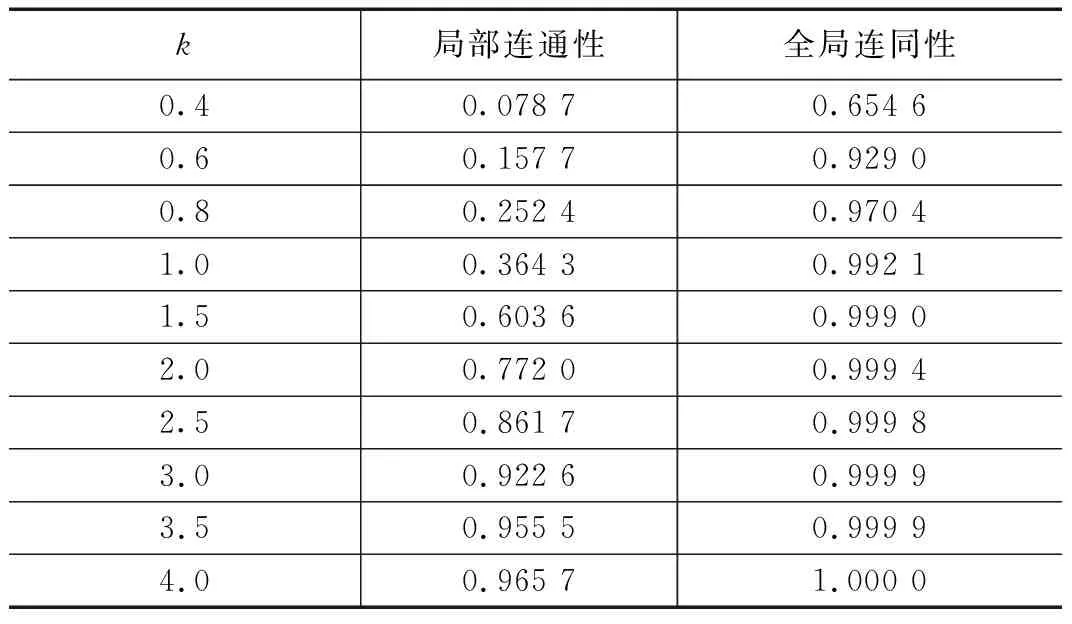
表2 仿真结果
3.3 内存开销和运行时间
在无线传感器网络协议设计中,长寿命是关键目标。在本文模型中,我们最小化相邻节点之间发现公用密钥空间的广播数据需求,1-跳广播消息长度为:
节点ID的大小+ Rv的大小+3×H的大小(bits)
(14)
用于存储从多项式得到的密钥材料的内存大小为:
M=3×(t+1)log2q+节点ID的大小+Rv的大小(bits)
(15)
这个值连同共享一个多项式的节点数量影响成对密钥建立之前节点受攻击的恢复能力。这将在3.4中详细讨论。
将本文模型与文献[13]~[15]的模型在不同网络规模下的内存开销即所需要的内存大小进行比较,结果如表3所示。从表3可见,不同模型随着网络规模的增大,内存开销也增大,这是因为要完成更多节点间的密钥空间计算、交换和配对,但是本文模型的内存开销始终是最小的。这是由于本文模型在密钥建立阶段将全部节点进行集群分组,而且尽可能使传感器节点均匀分布,减少了密钥分配和建立阶段计算空间的存储开销和信息交换。
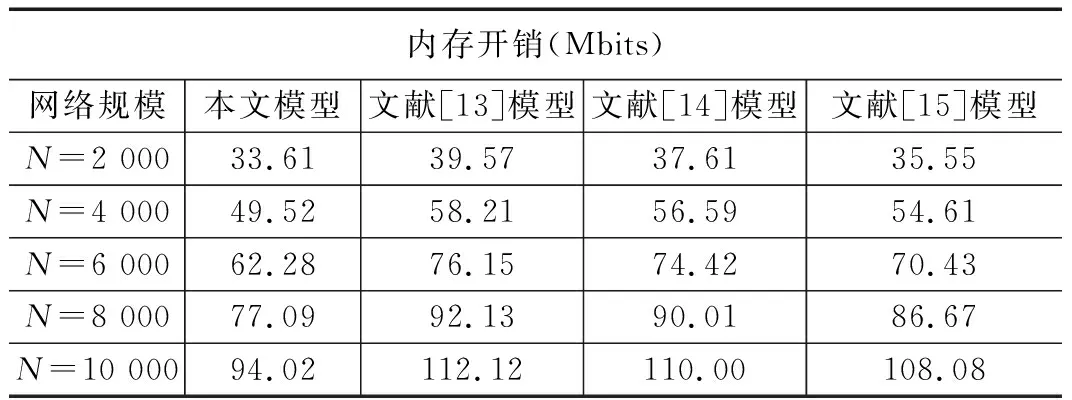
表3 不同模型的内存开销比较
将本文方案与文献[13]~[15]的模型在不同网络规模下的的运行时间进行比较,结果如表4所示。从表4可以看到,不同模型随着网络规模的增大,运行时间也是增加的,这是由于随着节点数目的增大,不仅增加了节点部署和多项式分配的时间开销,更重要的要花更多时间完成密钥空间的计算和配对;但是本文模型在密钥建立阶段采用了密钥材料的预加载和1-跳密钥空间发现消息来实现相邻节点的共享密钥空间分配,所以仍然有最小的运行时间。
表4 不同模型的运行时间比较
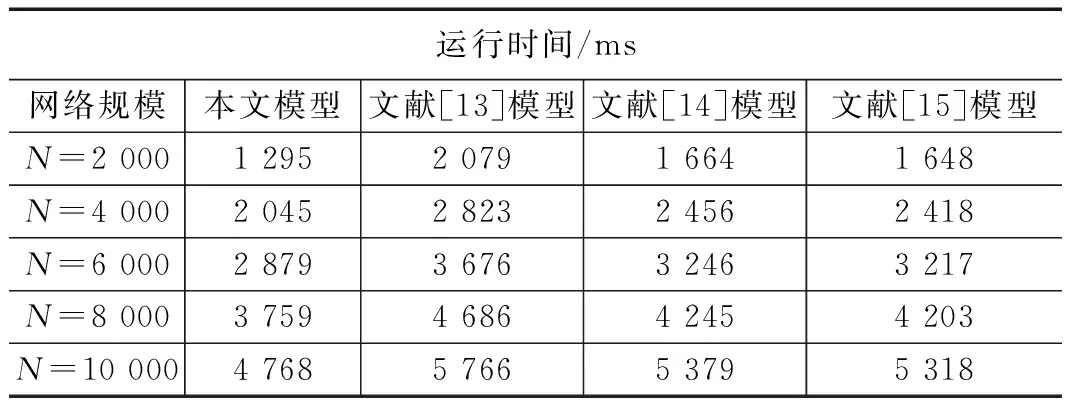
运行时间/ms网络规模本文模型文献[13]模型文献[14]模型文献[15]模型 N=2 0001 295 2 0791 664 1 648N=4 0002 045 2 8232 456 2 418N=6 0002 879 3 6763 246 3 217N=8 000 3 759 4 6864 245 4 203N=10 0004 768 5 7665 379 5 318
3.4 对捕获节点攻击的恢复能力
由于传感器网络工作环境通常比较恶劣,传感器节点很容易被捕获并泄露信息。捕获的传感器节点数量依赖于多项式的次数,也就是存储密钥材料的内存。对捕获节点攻击的恢复能力定义为当x个节点被攻破时,泄漏一个多项式的概率,这相当于在未受损的传感器节点之间泄漏直接密钥。
文献[14]表明,基于多项式的方案具有t-安全性:即除非公开了一个二元多项式的超过t个多项式共享,否则对手不会知道使用该多项式建立的非受损节点的成对密钥。因此,本文模型的安全性依赖于共享同一多项式的传感器节点的平均数量,即期望位于3个相邻六边形单元格中的传感器节点的数量。
把期望位于一个单元格内的传感器节点的平均数量表示为Nc,则共享一个多项式的传感器节点的平均数量可计算为:
(16)
式中,ϖ为传感器节点密度。
如前所述,存储密钥材料的内存需求为M(bits),因此二元多项式的次数为:
t=[M/3]-1
(17)
只要NG≤t,本文模型就能很好地抵抗节点捕获。换句话说,受损的传感器节点不会导致非受损传感器节点之间共享的直接密钥受损。
由于攻击是随机的,假设网络中有一小部分传感器节点pc被攻击者破坏。在具有多项式共享的NG个传感器节点中,正好有i个传感器节点被攻击的概率可以计算为:
(18)
因此,二元多项式被破坏的概率可计算为:
(19)
图2所示为本文模型在不同部署点距离d节点受损攻击时仿真得到的网络恢复能力。可以看到,部署点距离越长即单元格越大,对节点受损攻击的网络恢复能力越脆弱。这是因为当单元格较大时,在一个单元格中有更多的传感器节点共享一个密钥空间,从而导致安全性降低。
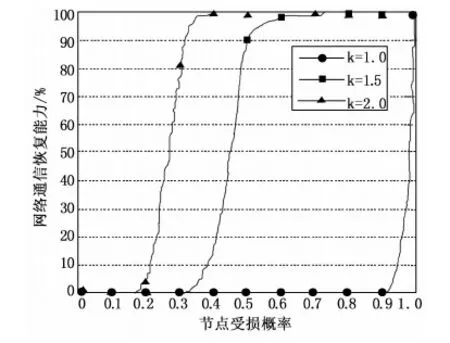
图2 不同部署点距离下节点受损攻击时网络的恢复能力
图3所示为本文模型在不同内存大小M(bits)情形下节点受损攻击时仿真得到的网络恢复能力。可以看到,随着内存的增大,网络的恢复能力增强,这是因为多项式的次数更高,就越不容易被攻击破坏。
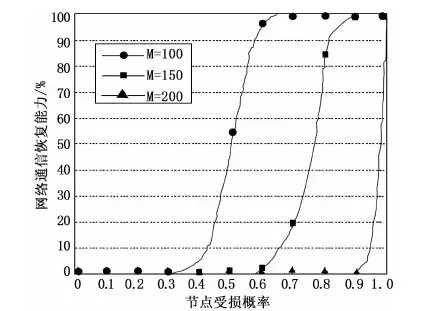
图3 不同内存大小情形下节点受损攻击时网络的恢复能力
图4所示为不同模型的传感器节点被攻击时的网络恢复能力比较。可见,与文献[13]、[14]和[15]模型相比,本文模型在节点受损时的具有更好的安全性。这是由于本文模型存在密钥预分配阶段,而且离线服务器为每个集群生成一个包含足够多的t次对称二元多项式多池,然后将每个多项式分配给每个集群中的所有传感器节点,以确保每个节点都要存储3个t次二元多项式的共享知识,对手更难获得融合多个节点的密钥材料,从而提高了安全性。
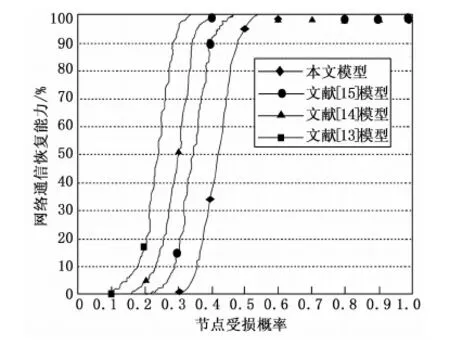
图4 传感器节点被攻击时不同模型的网络恢复能力比较
4 结束语
本文提出了一种可实现的基于多项式的密钥预分配模型,它利用了高斯分布的预部署知识。同时还表明了模型在网络连通性、通信开销和内存需求等方面具有的优势。它还可以抵御非捕获节点间受损附加密钥的攻击;未来的研究将集中在部署误差率对网络连通性的影响和分析多跳间接密钥建立的可能性。
