指定域多无人机协同目标跟踪研究

朱代武，刘 豪，曾婧涵，孙永鹏

(中国民用航空飞行学院,四川 广汉 618307)

0 引言

无人机系统是目前无人系统领域发展最快、水平最高、实战应用最多的一类空中系统，而多无人机对重点区域进行协同侦查、目标搜寻及目标跟踪是空中作战系统中实用的技术领域。多无人机协同主要从信息融合与资源互补两方面对任务进行组织分配，在多UAV并行过程中，每架UAV所拥有的信息源均为自身传感器所捕获，无人机集群中的所有UAV进行综合态势感知与信息融合，提供给UAV主控系统以进行任务分配与调度，进而提高任务执行效率。然而在实际任务中，受UAV性能、任务需求和环境因素影响与制约，对多UAV进行协同控制是一个极其复杂的过程，其复杂性主要体现在：(1)任务所处环境的复杂性；(2)多无人机UAV个体间的差异；(3)任务需求的复杂性 ；(4)计算与通信的复杂性[1-2]。

为解决多无人机在多复杂性条件下的协同跟踪问题，国内外学者做了大量的工作，如传统方法以搜索论[2-3]为基础，从最大化目标发现概率的角度预先设计覆盖作战区域的多目标搜索方法。然而多无人机协同作战是一个动态过程，一般情况下目标处于移动状态，无法进行预先规划，只能根据作战跟踪过程中的实时探测信息和环境信息进行实时决策。针对动态作战过程，目前一类重要的办法是基于搜索图的办法，如占用图[4]、概率图[5]、信息素视图[6]等，此类方法都是通过构造反映目标和环境信息的二维离散地图，并基于实时探测消息更新，在当前搜索图上进行求解[7-9]。对于多无人机协同作战而言通过离散地图上的中央节点来维护全局的搜索图信息，最后基于当前多无人机状态采用滚动优化方法求解该群的最优化轨迹及覆盖区域，然而集中式计算数据量较大，且机群间不同位置的运动姿态各不相同，存在计算时间过长无法进行有效时间内自主决策。

为解决数据量大及计算复杂问题，提高动态规划效率，基于预先分配结果进行动态任务分配。以战术多无人机执行协同打击任务为背景，针对具有战术目的的持续跟踪(持续跟踪，表示跟踪目标尽可能处于观测平台的传感器范围内，在复杂环境特别是城市环境作战，由于传感器视线遮挡、飞行空域限制等需要多无人机协作以维持目标跟踪任务的鲁棒性[10])跟踪作战，研究战术无人机协同目标跟踪优化方法，验证所选取方法的有效性。

1 协同目标跟踪下的协同目标跟踪

系统中的智能个体根据个体之间的局部交互信息对自身的行为进行动态调整。其中集群行为(collective behavior)是集群个体经由所关联耦合合作方式而涌现出来的自组织运动模式，其关联耦合方式的差异性也会促使集群行为产生差异。如何对个体的行为规则进行构建、刻画与分析、关联耦合结构与运动特性，使得一个融合性的系统在运动过程中能够保持一致性，以实现期望的集群行为与完成预期的复杂任务。

UAV跟踪开始阶段，UAV跟踪续航阶段与UAV跟踪结束阶段为多无人机机动目标跟踪的一个完整过程。即首先跟踪起始阶段利用无人机传感器所携带的量测信息建立新的目标规划航迹，其中较为典型的跟踪方法有连续多次扫描和基于目标设定下的后验概率决策分析方法；其次跟踪续航阶段通过UAV所搭载的双向数据传输链路来实现量测信息与已确定航迹的配对拟合，然后利用现有的信息融合处理技术对各个目标的状态数据参数进行获取存储，进而对已确定的规划目标航迹进行更新；跟踪结束阶段为跟踪开始阶段的逆向过程，即目标离开跟踪空间时消除多余的预测目标航迹。

1.1 协同跟踪下的多无人机控制

无人机集群通过组建高动态、可扩展、智能化的无人机集群网络，能够提升无人机的适应能力，协同完成复杂任务。针对无人机集群协同技术，介绍在路径规划、态势感知和任务协作等领域的应用研究，通过分析无人机集群网络协同的发展历程及传统方案的不足，提出未来的无人机集群协作将是多智能体的无人机集群智能协同，给出了实现框架[11]。

由于UAV系统自我组织控制能力的增强，地面操纵正在实现由手动操纵向机器学习监督式控制过渡。目前UAV任务控制系统通常采用分层递阶结构框架[12]，该框架中为面向战术任务的4层任务控制结构，分别为多无人机战术层、多无人机策略层、多无人机控制层和多无人机执行层[13-16]。其中战术层主要依据战术任务要求，分析任务特点、制定任务时序与逻辑过程与指定策略优化等；策略层主要结合策略优化要求和环境约束，融合目标感知信息、与其他单位交互协同等；控制层基于得到的策略层进行航点跟踪计算、速度保持与互联云台控制等；执行层从物理层面控制平台及其任务载荷，其结构如图1所示。

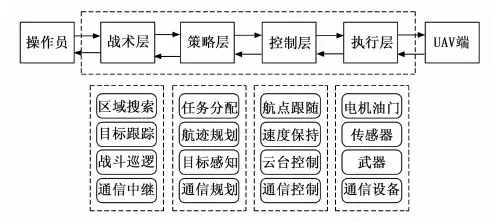
图1 战术UAV系统分层战术任务控制系统[12]

由于实际战争环境复杂且动态变化，机载传感器获取的目标信息存在高度的不确定性，因此对目标跟踪、区域搜索、感知与规避等战术任务，在任务控制系统的策略层，可采用基于主动感知的任务求解过程，任务过程包含目标感知、估计猜测以及任务优化等模块[17]，该战术模块如图2所示。

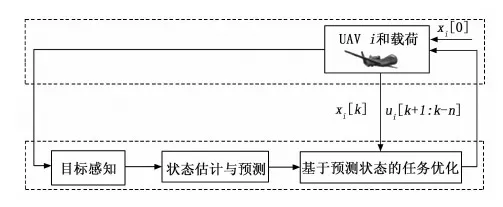
图2 战术任务的主动感知求解过程[12]

1.2 多无人机协同跟踪模型

多无人机的协同跟踪是根据其性能参数、传感通信条件、集群个数等为基本约束条件(影响多无人机运行效能的因素很多，如航程、航时、飞行速度、飞行高度、单个无人机性能等，为便于量化分析需对多参数进行整合。)，以实现多任务、多层次、多范围内的最优化处理为目标函数，并根据实际情形需要将任务进行分配处理，以求达到任务处理时满足全局收敛与时间最短[18]。

假定任务区域中分布着N架UAV(记为xi,i=1,2,…,N)和具有部分先验消息Pta的被跟踪目标xi，每架UAV均可获得协同跟踪目标的观测信息zi(i=1,2,…,N)，且各UAV之间相互独立。要求在规定任务时间内协调优化各UAV控制输入ui，可以得到最优化控制输入ui*。

因多UAV协同目标跟踪存在3个层次的协作，需融合不同无人机对跟踪目标的侦查以获取目标最优化处理；其次使用跟踪性能最优对航迹进行协作；最后在任务控制方面需进行更高层次协作。对于集中式控制结构可采用如下协同跟踪模型[19]:

u*[1,…,L]=argmaxJ

(zi[k+1:k+L],xi[k+1:k+L],xt[k+1:k+L])

(1)

s.t:

xt[k+1]=f(xt[k])+q[k]

(2)

xi[k+1]=a(xi[k])+b(ui[k])

xi[k]∩RL=φ

(3)

zi[k]=hi(xt[k],xi[k])+vi

i=1,2,…,N

(4)

其中:u=[u1,…,uN];ui= [uiδ,uiγ,uiV]表示UAV控制输入；δi[k],γi[k],Vi[k]分别对应UAV的偏航角、俯仰角和速度，而对应上述3个变量的控制输入uiδ[k],uiγ[k]与uiV[k]需要满足平台的动力学约束；J(·)表示航迹优化的效能函数；f(·)表示目标状态转移模型；q[k]～N(0,Q[k])是k时刻目标状态的过程噪声；L为战术航迹优化的时域长度所对应的执行时域的数目；a(·)为UAV状态转移模型；b(·)为UAV控制输入的过程模型；RL为UAV禁止飞行区域集合；h(·)为对应无人机对目标的状态观测模型；vi为无人机测量噪声。

因UAV个体之间相互独立，可用分布式控制结构进行协调，则对每个UAV节点i进行航迹优化，则式(1)～(4)改进后如下:

ui*[1,…,L] = argmaxJi

(zj[k+ 1:k+L],xi[k+ 1:k+L],xt[k+ 1:k+L])

(5)

s.t:

xt[k+1]=f(xt[k])+q[k]

(6)

xj[k+1]=a(xj[k])+b(uj[k])

xj[k]∩RL=φ

(7)

zj[k]=hj(xt[k],xj[k])+vj

j∈{i}∪Vi

(8)

因卡尔曼滤波需对UAV动态系统进行精确计算，并且对高斯噪声的统计特性有精准要求，而在实际多UAV协同跟踪系统中往往无法得知，尤其对于未知复杂环境的目标跟踪领域。因卡尔曼滤波为在时间域内的递推，其迭代计算为预测-更新的循环过程，因该迭代单向有序，从而无需占有过多存储空间对统计数据进行处理，从而便于计算机操纵系统的高效响应。在实际递推的处理过程中往往采取卡尔曼信息滤波器，即在预测和更新两个步骤中通过递推形式计算协方差矩阵的逆，具体可对其定义为：

(9)

(10)

(11)

(12)

当多UAV协同跟踪系统状态n大于所需量测维数p时，采用卡尔曼滤波形式较为精确，因为此时所需的求逆矩阵为p×p;当主控系统状态维数n小于已量测维数p时采用信息滤波形式较为合适，此时对应的求逆矩阵为n×n，且采用信息滤波易于处理多传感器信息的融合问题。同时在该优化结构模型中设定单个UAV为群网络节点，且只在面向自己的控制指令下进行优化升级处理，每个节点的效能函数可与网络中临近UAV的数据进行融合处理，并在适当时候进行耦合搭建。

1.3 多UAV下的集群系统控制方式

在目前多无人机集群运行控制中，常见的控制方式有4种，分别为:集中式、分布式、分层式与自组织式，以下就4种进行简述说明：

1.3.1 集中式协同运行控制

集中式控制是指UAV由集群中的主机带领，由主机进行主要的计算和指令发布，其他无人机处于次要或者辅助位置；或者由集群控制的外部平台或者地面基站充当控制单元，多无人机运行过程中的无人机接收执行数据与指令，并适当向“控制者”进行信息反馈。集中式的控制是建立在对全局信息掌握的基础上，每架UAV的位置信息、v、姿态与运动目标信息进行交互处理。

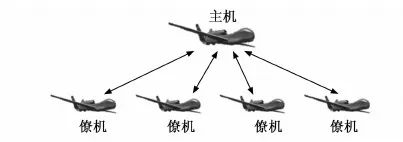
图3 多无人机协同集中式结构

1.3.2 分布式协同运行控制

分布式控制是指系统的控制结构是分布式的。分布式的控制需要建立在集群多无人机的局部信息的基础上，每架无人机要将自己的位置信息、v、姿态与运动目标信息与其他无人机进行交互信息处理，在分布式控制下每架UAV装备相对独立的控制单元，通过多无人机之间的协作去完成任务。这种控制不仅仅依赖于中心控制单元，在单架UAV通信失常时，可与附近UAV进行通信数据互补以增强多无人机协同运行的安全性与稳定性。

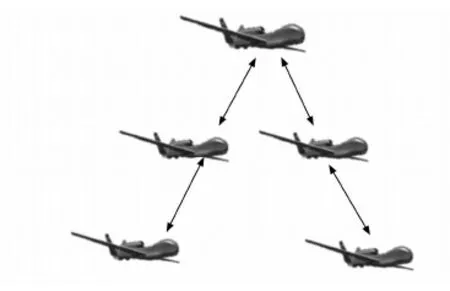
图4 多无人机协同分布式结构

1.3.3 分层式协同运行控制

在多无人机协同运行中单机进行水平交互的同时加上垂直交互来实现冲突解脱。当无人机协同运行群中个体数目小于等于6时，使用集中式协同运行或者分布式协同运行效果较好；当协同运行中的无人机数量大于6时，适合对无人机进行分层管理，实际分层控制结构根据任务组织情况、无人机运行所处的外部环境等因素进行综合考量。

1.3.4 自组织式协同运行控制

自组织式协同运行类似于生物集群的方式，以集群行为对多无人机进行协调控制集群行为的产生以及运行机制比较简单，但是考虑到无人机个体容易受到附近无人机的干扰，在对无人机没有集中控制的前提下，个体无人机容易通过局部简单的交互行为使得全局无人机群出现自组织、协作等一些等挑战性的无人机协同运行，这种技术在复杂系统中称之为能力涌现。通过交互作用或者协作行为，组织较为分散的无人机单体能够通过耦合作用表现出较强的整体优势，能够完成较为复杂的任务。

图5 多无人机自组织式结构

2 面向持续协同跟踪模型优化

持续协同跟踪的首要条件是在复杂环境中始终保持UAV传感器观测范围对目标的有效覆盖，其在线观测优化效能函数为:

J(zi[k+1:k+L],xi[k+1:k+L],xt[k+1:k+L])=

λ1·λ(P(xt[k:k+L]|z1:N[k],xt[k-1]))

(13)

式中,λ1、λ2为加权系数；Sen为传感器对目标的覆盖效能函数，取值如下:

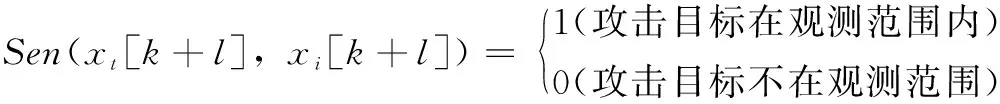
(14)

将式(13)带入式(1)即可得到集中结构下面向持续跟踪的多无人机协同优化模型。此外除需满足运动学约束外还需满足以下两项约束：(1)跟踪目标处于可视范围内；(2)处于指定空域以内。

跟踪目标是否能够被感应捕捉，除感应器自身限制外还与外界环境息息相关。有效的无人机感知系统通常包含多种传感器，多源信息融合可以对来自于多个传感器的数据进行多层次、多级别和全方位的综合处理，得到对环境的最佳描述[20]。

针对存在障碍物的复杂环境，假设地形地物信息已知，可通过计算目标的可视域而非UAV传感器探测范围对问题进行简化[21]。令XV(x)为跟踪目标x的可视范围，XhV(x)为x在高度为h时的可视范围，其对应的可视范围如图6所示。

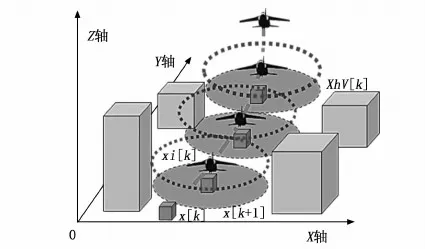
图6 目标可视区域示意图

为便于计算以飞行高度最低的UAV的可视域作为问题约束，即h=min(hi)。在获得可视区域内通过判断UAV是否位于跟踪目标可视区域即可确定目标是否在作战中被侦查[22-24]。令第i架UAV在给定时刻k位于跟踪可视区域x[k]内可表示为Dxi[k]，且Dxi[k]属于XihiV(x[k]),其中D=[I3×3[0]3×(1+n)],hi对应UAV的飞行高度。此外作战环境中空域多元化会导致复杂度增加。令B={1,2,…,Nb}表示UAV飞越的空域集合，每个单元b∈B通过多面体R0b表示，则:

(15)

3 指定域协同跟踪实验仿真

为检验面向持续协同跟踪模型的有效性，在win10的运行环境下进行UAV协同仿真，同时采用MATLAB2018.a进行模拟仿真实现。仿真中采用远程侦查跟踪型UAV在复杂环境里对单个作战目标进行跟踪,UAV群中含有数量为37架(UAV单机机长1.65 m,翼展2.1 m,机翼展弦比5.7 m)。其中模拟地形区域范围为[-50,50]×[-50,50](单位:km);UAV飞行速度为50 m/s;最大偏航角速度为0.6 rad/s,UAV携带有测向和测距传感器，测量误差协方差为Vi=[25 m2,0.1 rad2,0.1 rad2];仿真时长为300 s；单步决策时间间隔为1 s。对应算法设置中令L=10,即估计未来10 s目标位置；计算相应控制序列记为k+10；进化算法的染色体数量为50；运行次数最大值为1 000；最长运行时间为2 s，并对UAV群协同运行边缘进行标记，标记后的多无人机运行如图7,8所示(标记地面跟踪点为原点，坐标为(0,0))。因UAV感知范围为0°～360°，可设定侦察半径Ro对目标区域360°空间进行连续探测。本文所选取UAV为中程巡航类型可设定Ro=4 km，令原点(0,0)为跟踪基准点，2R0为被跟踪目标辐射半径。同时考虑单UAV之间的协调性，可依次设定4R0与8R0作为目标跟踪扩展半径，如图7所示。

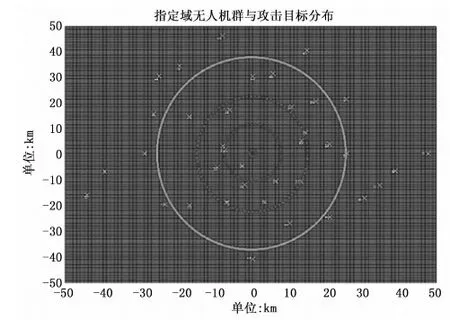
图7 指定域多无人机与跟踪目标分布

因UAV机长1.65 m，翼展2.1 m，取机长与翼展中的最大值作为无人机自控半径，即rCD=max(1.65,2.10)=2.10,[单位:m]；按照无人机运行手册规定，UAV之间运行距离lCD不得小于1.5 rCD，即在该实验中lCD=3.15 m。对指定域分布的多无人机进行标记，单个UAV标记半径为3.15 m，标记后的分布如图8所示。

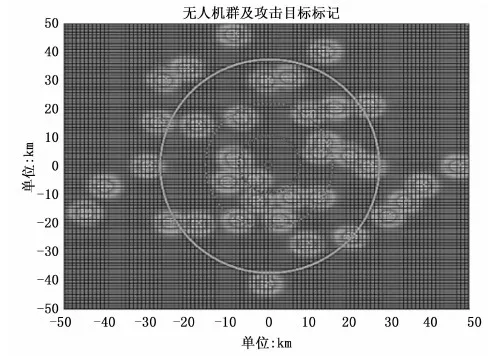
图8 多无人机协同跟踪目标标记

有限域内对多无人机边缘进行连接，可对有限域内多无人机跟踪范围进行缩小，进而提高协同目标跟踪的精准度，在缩小区域内对面向持续跟踪的多无人机协同进行卡尔曼滤波检验，将UAV数据带入上式可得对应实验结果如图9所示。

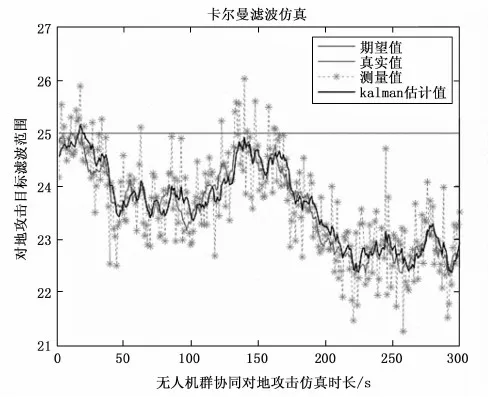
图9 无人机协同跟踪滤波范围

如图9所示，设定25(单位:m2)为期望值，即滤波值应小于等于该期望，实验表明测量值区间较为宽泛，其值区间为[21,28],区间的跨度保证了多无人机协同运行上的自主性与协调能力的重复发挥。当t=0时真实值为24.9(单位:m2)，kalman值为24.6(单位:m2)，说明通过利用面向持续跟踪算法在基础位上能够保证误差得到减小，且随着仿真时间的延长，测量值呈现随机分布状态更便于多无人机的机动协调飞[25]。同时kalman估计值与真实值拟合度更高，且远小于期望值，证明了多无人机在实际作战中对目标跟踪的精准性。对kalman滤波误差及测量误差进行对比分析，可知测量误差极限区间为[-1.5,1.5],kalman误差为[-0.5,0.5](因UAV机载传感装置，可协同物信息进行侦察，红色虚线框所示)，证明面向持续跟踪的多无人机协同误差相比于先知地形地物信息误差率缩小66.6%,间接证明了所使用模型在多无人机协同目标跟踪中的合理性[26]。

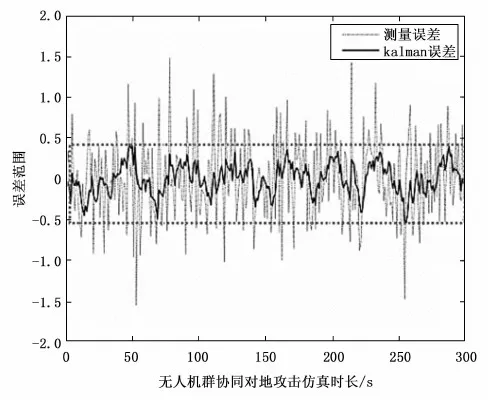
图10 多无人机协同运行误差对比

因所使用作战无人机具有测向和测距传感器功能，在相同实验条件下对采用主动感知策略与只考虑跟踪目标不考虑主动感知算法(记为k+0)进行比较，其跟踪目标被观测次数与目标位置平均误差结果如图11(a)与11(b)所示[27-30]。

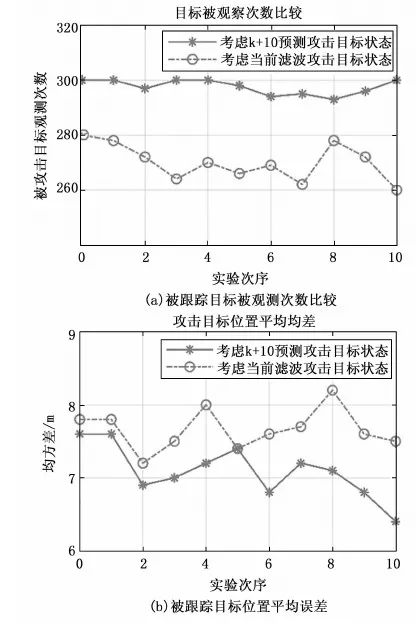
图11 有/无主动感知策略跟踪性能比较

由图11(a)可以得出采用k+10时刻被跟踪目标预测状态进行优化后能够提高跟踪目标被探测次数，平均29次，被跟踪目标至少在多无人机传感器观测范围内的时刻数为300次左右。图11(b)为融合滤波得到的被跟踪目标位置平均误差，较之于k+0相比基于k+10时刻被跟踪目标估计误差降低约13%。

4 结束语

因多无人机协同是由一定数量单功能和多功能UAV共同组成，在交感网络的支撑作用下，无人机节点之间进行信息交互与反馈、激励与响应等交感行为[31]；且多UAV具有能力涌现的特点，可实现单主控平台行为自主决策、平台间行为协同决策[32]，最终产生能力涌现的自主与他助融合的辅助空中移动系统，同时多无人机协同运行不是单无人机的简单编队，其集群能力也不是诸多控制服务平台单一能力的简单叠加，而是由多航空器控制下的科学聚集，经过协同自组织实现自组织与行为调控机制的有机耦合。然而由于现实环境中存在的UAV系统复杂性、任务复杂性、时间敏感性、计算复杂性、通信复杂性等各种影响因素叠加在一起，使得对无人机自主协同控制成为热点[33]。为此本文提出了面向持续跟踪的多无人机协同模型不仅能够有效实现被跟踪目标的侦察工作，并能够在充分发挥多无人机自组织能力基础上实现目标状态的估计[24]。由于未来环境复杂、对抗性日益增强、任务的多元性[25]，可能存在算法失效问题，为此我们未来研究的重点是多算法融合下多无人机协同作战及利用拓扑结构对其代价函数进行构建。